Использование метода дополнительного построения при решении геометрических задач

Использование метода дополнительного построения при решении геометрических задач

Мы знаем, что любое решение геометрической задачи начинается с построения чертежа.

При этом на чертеже всегда обозначаем только то, что дано в условии. Такой чертеж называют «естественным». Но на таком чертеже иногда трудно увидеть взаимосвязь, то, что ведет к успешному решению задачи. Поэтому чертеж «дополняют».

При таком подходе к решению задачи, явно видны взаимосвязи, которые дадут путь к решению задачи.

Рассмотрим один пример решения такого типа задачи:

Задача:

Длины основания CD диагонали BD и боковой стороны AD трапеции ABCD равны между собой и равны p. Длина боковой стороны ВС равна q. Найдите длину диагонали АС.

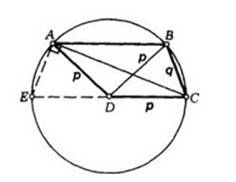Решение:

В данной трапеции ABCD сложно сразу увидеть связь между данной диагональю АС и другими отрезками.

Но если принять во внимание, что точка D равноудалена от точек А, В, С и провести окружность с центром в точке D радиусом p, достроить данную трапецию до равнобедренной трапеции ABCE, то из прямоугольного треугольника АСЕ можно легко найти АС: