Использование визуальных моделей при решении математических задач профессионального содержания

Использование визуальных моделей при решении математических задач профессионального содержания

Работа прикладного характера подразумевает достижение конкретного результата, который будет иметь практическое применение в жизни. В данном случае отсутствует потребность в теоретическом обосновании и получении опыта. Основная цель работы заключается в производстве действительно нужной и востребованной в дальнейшем вещи или предмета.

Прикладная и практическая направленность обучения – одна из содержательно-дидактических линий, тесно связанная с другими линиями (функциональной, числовой и пр.) школьного курса математики.

Прикладная направленность обучения математике предполагает ориентацию его содержания и методов на тесную связь с жизнью, основами других наук, на подготовку обучающихся к использованию математических знаний в предстоящей профессиональной деятельности

Практическая направленность обучения математике предусматривает ориентацию его содержания и методов на изучение математической теории в процессе решения задач, на формирование у обучающихся прочных навыков самостоятельной деятельности, связанных, в частности, с выполнением тождественных преобразований, вычислений, измерений, графических работ, использованием справочной литературы, на воспитание устойчивого интереса к предмету, привитие универсально-трудовых навыков планирования и рационализации своей деятельности.

Определения понятия задача профессионального содержания рассмотрены в таблице 1.

Таблица 1 – Различные подходы к определению понятия математические задачи профессионального содержания (сост. авт.)

При обучении математике, для реализации профессиональной направленности, используются задачи и вопросы, которые разрабатываются преподавателями специальных дисциплин и мастерами производственного обучения. Профессиональный характер может быть заложен в тексте задачи или выражен с помощью рисунка, чертежа, схемы, инструмента и тому подобное.

Задачи с профессионального содержания составляются на основе тех знаний и  умений  по  математике,  которые  непосредственно  связанны с профессиональными знаниями и умениями. Они помогают заинтересовать обучающихся, позволяют обратить внимание на применение математических знаний в процессе обучения профессии.

При составлении задач, ориентированных на связь с профессией, большое внимание уделяется их формулировке, так как форма постановки задачи определенным образом направляет познавательную деятельность обучающихся. Решение задач с профессиональной направленностью способствует формированию у обучающихся умений находить в профессиональной ситуации существенные признаки математического понятия, подводить объект под математическое понятие, использовать его в новых условиях. Поэтому задачи с профессиональной направленностью предусматривают умения применять теоретические положения к решению практических задач, а также на развитие пространственного воображения, вычислительных навыков и графических умений обучающихся, расширяют их профессиональный кругозор, формируют обще трудовые умения и навыки при работе с измерительными приборами, таблицами, справочной литературой.

Дидактический материал с профессиональной направленностью применим на различных этапах урока, но чаще всего при закреплении знаний.

Тщательный анализ учебного материала, выносимого на урок, позволяет определить, что обучающийся должен узнать, что следует повторить, чему научиться. При подготовке к уроку определяются основные понятия, теоретические положения, раскрывающие содержание темы урока, а также объем материала, его связь с ранее изученным материалом; его воспитательную и профессиональную значимость.

Если изучаемый материал профессионально значим, то определяется его характер (обязательный или информативный), вид связи с содержанием специальных предметов (предшествующая, сопутствующая, перспективная), подбираю задачи, соответствующие целям урока, определяю их место в структуре урока, время и приемы работы с ними.

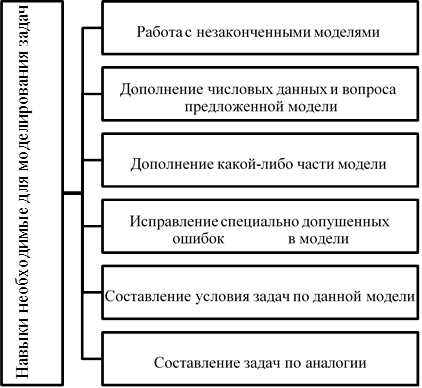Рисунок 1. Навыки необходимые для моделирования задач профессионального содержания (по Е. Н. Эрентраут, 2009)

Помогая обучающимся в поисках решения задачи, нужно сделать схематический рисунок или чертеж к задаче; объясняя прием вычисления, сопровождая пояснение действиями с предметами и соответствующими записями и так далее.

При этом важно использовать наглядное пособие с визуальными моделями своевременно, иллюстрируя самую суть объяснения, привлекая к работе с пособием и пояснению самих обучающихся. При раскрытии приема вычисления, измерения, решении задачи и так далее надо особенно четко показывать движение (прибавить-придвинуть, вычесть-убрать, отодвинуть).

Сопровождение объяснения рисунком (чертежом) и математическими записями на доске не только облегчает обучающимся восприятие материала, но и одновременно показывает образец выполнения работы в тетрадях.

Например: как расположить чертеж и запись решения в тетради, как обозначить периметр с помощью букв и тому подобное. При ознакомлении с новым материалом и, особенно, при закреплении знаний и умений надо так организовать работу с визуальной моделью, чтобы учащиеся сами оперировали ими и сопровождали действия соответствующими пояснениями. Качество усвоения материала в большинстве случаев значительно повышается, так как в работу включаются различные анализаторы (зрительные, двигательные, речевые, слуховые). При этом учащиеся овладевают не только математическими знаниями, но и приобретают умения самостоятельно использовать наглядные пособия визуальными моделями. Учитель должен всячески поощрять обучающихся к использованию визуальных моделей, к самостоятельной работе. Важным условием эффективности использования визуальных моделей является применение на уроке достаточного и необходимого количества наглядного материала. Если визуальных моделей применять там, где этого совсем не требуется, то они играют отрицательную роль, уводя детей в сторону от поставленной задачи. Визуальные модели, использованные в этом случае, не только не помогает, но наоборот, задерживает развитие умения решать задачи, то есть выбирать действие над числами, данными в условии.

Скачано с www.znanio.ru