Испытания Бернули

Модуль 9

Испытания Бернулли

Контрольная работа

Подготовила Бондаренко Надежда Ивановна.

Решение задач.

1.      Будут ли испытаниями Бернулли следующие серии опытов (если да, то найдите р и q в тех случаях, когда это возможно):
а) десятикратное бросание кубика; успех выпадение шестерки;
б) ответы у доски на уроках математики в течение месяца; успех получение пятерки;
в) проверка лампочек при их продаже в магазине; успех лампочка бракованная;
г) вытаскивание 10 карт из колоды без возвращения; успех вытаскивание красной масти.

Решение.

а)        да, , ;

б)        да, за ответ у доски ученик может получить оценки: 1, 2, 3, 4, 5, следовательно , ;

в)        да; ,

г)         нет, результаты опыта зависимы, так как карты не возвращаются в колоду.

2.      Какова вероятность, что при бросании шести кубиков выпадет хотя бы одна шестерка?

Решение.

Вероятность того, что при бросании шести кубиков выпадет хотя бы одна 6, равна: ,

а вероятность того, что не выпадет, равна .

Данная серия опытов будут являться испытаниями Бернулли, тогда воспользуемся формулой Бернулли: .

Число сочетаний находится по формуле .

Найдем значение вероятности по формуле Бернулли при  (т.е. выпадет ходя бы одна шестерка) и  (бросают 6 кубиков): .

Вычислим .

Тогда .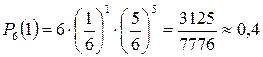

Ответ: 0,4

3.      В подъезде горит 5 лампочек. Вероятность, что любая лампочка не сгорит в течение ближайшего месяца, равна 0,2. Какова вероятность, что в течение месяца
а) сгорят все лампочки;

б) сгорит ровно одна лампочка;

в) останутся гореть, по крайней мере, 3 лампочки.

Решение.

а)        ; .

Найдем вероятность перегорания всех ламп

;

.

Ответ: 0,00032

б)        Сгорит одна лампочка, т.е. останется 4 лампочки

.

Ответ: 0,0064

в)       

.

Ответ: 0,0512

4.      Вратарь футбольной команды отражает в среднем каждый третий пенальти. Сколько пенальти из пяти он отразит, скорее всего? С какой вероятностью?

Решение.

;

Найдем ожидаемое число удач при  с вероятностью успеха

.

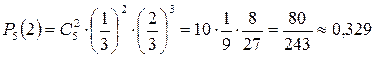Ответ: 2; 0,329

5.      Завод отправил заказчику 10000 стандартных изделий. Средняя доля изделий, повреждаемых при транспортировке, составляет 0,02%. Найдите вероятность того, что в этой партии будет повреждено.
а) ровно 3 изделия;

б) не более 3 изделий.

Решение.

а)        Вероятность того, что изделие будет повреждено при транспортировке, равна  и , так как p - мала, а N – велико и Применим формулу Пуассона

/

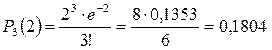Ответ: 0,1804

б)        Для события «будет повреждено не более 3 из 10000»,  и .

Ответ: 0,8572