Исследовательский проект "Роль математики в профессии парикмахера"

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ПЕРМСКОГО КРАЯ

ГОСУДАРСТВЕННОЕ БЮТЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«КРАСНОКАМСКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»

 

 

 

 

Исследовательская работа (проект)

 

Роль математики в моей профессии парикмахер.

 

Выполнили:                                              Торопова Юлия,  Копысова Евгения                                             Руководитель работы:   Моисеевких И.И. – преподаватель математики

 

                           

 

 

                         

 

 

        

 

 г.Краснокамск

                                   

                                    

                                                 Содержание

   Введение………………………………………………………………… 3
   Основная часть…………………………………………………………....4

          Конические сечения

           Гладкие кривые

           Геометрия стрижки

          Особенности формы лица

           Бигуди и их форма

           Исторические причёски

           Коническая стрижка

   Вывод…….………………………………………………………….…… 9
   Список литературы……………………………………………………....10
   Приложения………………………………………………………..……..11
  

 

 

 

 

 

 

                                       Введение

       Актуальность:  В школе очень большое внимание уделялось математике. Предмет достаточно сложный, мы еле сдали его в школе и с облегчением вздохнули, так как  выбрали рабочую профессию. Но, поступив обучаться, мы с удивлением узнали, что математика и здесь занимает ключевое значение, а мы очень не любим устно считать, опасаемся трудных задач, больших вычислений, а   задачи предпочитаем только на смекалку. Студенты не понимают, зачем  нужна математика в рабочей профессии. Мне захотелось им помочь, раскрыть им глаза, научить любить эту науку, показать важность математики. Поэтому  я  взялась за исследование.

Проблема: Какую роль играет математика в нашей жизни? Собрать доказательный материал и убедить товарищей  изучать математику лучше, заинтересовать их.

Гипотеза:   Математические знания выручают в различных жизненных ситуациях, математика применяется в различных профессиях. Математика служит во благо человеку.

         Многие люди в своей жизни задавались вопросом «А зачем математика в моей профессии?», так и я, придя, учится в Краснокамский политехнический техникум, задалась вопросом – «А,  зачем нужна математика в моей бедующей профессии?».  Для того, что бы решить этот вопрос я занялась глубоким изучением этого предмета. И к концу второго курса я полностью уверенна, что без математики в профессии парикмахер быть высококлассным специалистом не возможно. Вопрос «Математика в бедующей профессии» - является актуальным у молодого поколения. Предмет исследования: значение математики в профессии парикмахер.

В данной работе я покажу вам прямую взаимосвязь знаний и умений парикмахера в своём искусстве и владение им  курсом математики. Приведу примеры математических понятий,  используемых в прическах и стрижках.

Цель моей работы: Исследовать литературу о математике, собрать данные и обработать информацию о применении математических знаний в профессии парикмахер, для стимулирования студентов к качественному изучению математики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Основная часть

Приступив к изучению математики, с мыслью о взаимосвязи этого предмета с нашей профессией, мы сразу встретились с такой темой, как «Графики элементарных функций». Эта тема напрямую связна с нашей профессией.
       Знание основных элементарных функций, их свойств и графиков не менее важно, чем знание таблицы умножения. Они как фундамент, на них все основано, из них все строится и к ним все сводится. Так  и в стрижках от линий и изгибов волос многое зависит.
       И так рассмотрим графики элементарных функций:

 

 

 

 

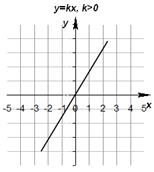    Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)  

 

 

                                                     

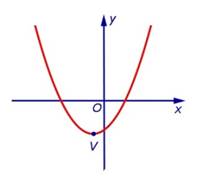
Парабола - график функции квадратного трёхчлена у = ах² + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax² + bx +с =0 (Рис. 2)

 

 

 

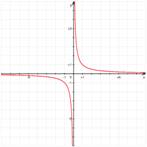
Гипербола - график функции  . При а > 0 расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у = х(а < 0).  (Рис. 3)

 

 

                            

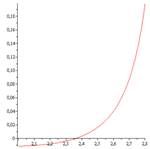
Экспонента- (показательная функция по основанию е) у = еx. (Другое написание у = ехр(х)). Асимптота - ось абсцисс. 0

 

 

 

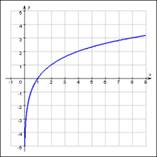
Логарифмическая функция y = log_ax (a > 0) 

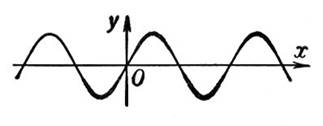
Синусоида(у = sinx.) - периодическая функция с периодом Т = 2π (Рис. 6)
у = а*sin(ωx+φ) - функция гармонических колебаний. Обозначения: а - амплитуда, ω - частота (ω = 2π/Т), φ - фаза (сдвиг).

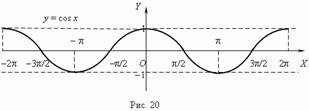
Косинусоида у = cosx (графики у = sinx и у = cosx сдвинуты по оси х на ).  

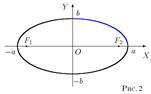
Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек ,F1, F2, называемых фокусами эллипса,  есть величина постоянная, численно равная длине большой оси этого эллипса:2a .  При этом расстояния между фокусами меньше данного
значения: F1, F2<2a 

 
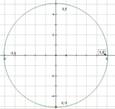
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
       Все эти графики, мы наблюдаем в линиях  причесок и стрижек, например прямую линию можно встретить в стрижках:  сессун, паж, пикси, каре, боб

 

 

 

 

 

 

Параболу можно наблюдать в стрижках:  каре на удлинение и каскад.

 

 

 

Гипербола так же встречается в экстравагантных стрижках.

 

 

 

 

Эллипс мы увидим в прическах с использованием валика для волос.

Окружность используется в прическах с косоплетением.

      Далее изучая предмет мы столкнулись с конусными сечениями. Модели конических сечений я изготовила на конкурс объёмных фигур во время декадника наук общеобразовательного цикла. Прочувствовав эти фигуры своими руками, мы отмечаем аналогию форм причёсок, стрижек  и их частей с объёмными стереометрическими фигурами, как эта тема, напрямую связанна с парикмахерским искусством.
И так что же такое конические сечения, и как они связанны с нашей профессией?
Конические сечения - это плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину. С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек, удовлетворяющих уравнению второго порядка. За исключением вырожденных случаев, рассматриваемых в последнем разделе, коническими сечениями являются эллипсы, гиперболы или параболы.
Мы рассмотрели такие конические сечения как :
Эллипс -  секущая плоскость пересекает все образующие конуса в точках одной его полости; линия пересечения есть замкнутая овальная кривая — эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса.

        Парабола - секущая плоскость параллельна одной из касательных плоскостей конуса; в сечении получается незамкнутая, уходящая в бесконечность кривая — парабола, целиком лежащая на одной полости.
        Гипербола - секущая плоскость пересекает обе полости конуса; линия пересечения — гипербола — состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса.
        Все эти виды конических сечений так же встречаются в стрижках и прическах, разных стилей и направлений.

    Следующей темой которая заинтересовала нас стала, гладкая кривая.
Функция  f называется гладкой на отрезке , если она имеет непрерывную производную  на этом отрезке.

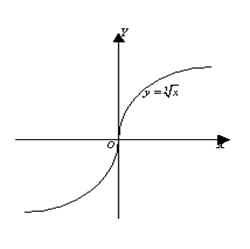
Примеры гладких кривых встречаются: в холодной укладке «Волны» и косоплетениях.

       Продолжая искать взаимосвязь математики и профессии парикмахер мы решили найти его в спец предмете.  На уроках спец. предмета мы встретились с математическими терминами, например таким как «Геометрия стрижки».
Геометрия стрижки - это понятие включает стрижку контрольной полосы с параметрами, основные из которых — это угол оттяжки пряди волос, длина прядей и угол среза.

      Продолжая изучать спец. предмет в очередной раз мы встретились с математическим элементами, геометрическими фигурами. Их можно наблюдать в формах лиц.
       Каждое лицо имеет свою форму, которая придает нам индивидуальность. Благодаря правильному определению формы можно понять: какая прическа подойдет больше всего, как наиболее выгодно подчеркнуть черты лица с помощью макияжа, какая бижутерия и одежда подойдет.  Существует 7 форм лица: овальная, круглая, квадратная, треугольная, грушевидная (трапеция), прямоугольная, ромбовидная.

 

Так же примеры форм лиц у известных людей.
     Рассматривая тему бигуди, мы заметили, что они все имеют форму цилиндра, а так же они имеют разные диаметры и длину (от которых зависит объем и упругость локона). Так и геометрическая фигура цилиндр имеет диаметр и высоту.

 

     Изучая историю причесок, мы снова обратили внимание на их форму, связанную с математикой, например  прически в Древнем Египте. Прически знати были геометрической формы, похожи на трапецию.

     В прическах стиля «Рококо» так же встречается большое количество геометрических фигур.  

Конкурсная работа обучающихся парикмахеров 2013 г.

      Название Рококо происходит от французского слова “рокайль”, которое означает “украшения”, “элемент декора и формы раковины”. Стиль получил развитие в живописи, скульптуре, архитектуре. Также стиль Рококо оказал большое влияние на костюм и прическу. Под воздействием нового стиля изменился эстетичный идеал. Если стиль Барокко был громоздким и тяжелым, как в костюмах, так и в прическах, то стиль Рококо наоборот принес деликатность, воздушность и легкость, утонченность, нежность. Исчезают черты силы и мужества в мужских портретах. И мужчины и женщины напоминают кукол одетых в шелк, без возраста и индивидуальности. Светлые парики, белила и румяна скрывали возраст.

 Во времена правления короля Людовика XV мужчины продолжают носить парики с большими локонами. Но с 1710 г. прически изменяются, становятся более утонченными, завивка выполнена малыми кольцами, позже их завязывали в хвост на затылке. Самыми популярными были прически “ке” и “бурс”.
     Еще на спец. предмете мы встретили геометрический термин- «Коническая стрижка».
Конические стрижки средней длины
Короткие слои, сделанные на супертонких, мягких прядях, представляют собой идеальную основу для создания потрясающей прически. Осваивайте современное искусство моделирования причесок и пользуйтесь глиной или воском для укладки и сывороткой для блеска, чтобы максимально полно раскрыть все преимущества вашего типа волос. Благодаря развитию парикмахерского искусства любая женщина может создать иллюзию объемной, пышной шевелюры. Средняя длина – идеальная основа для экспериментов с множеством моделей. Остановите свой взгляд на актуальнейших прическах, которые столь популярны среди наших любимых звезд. Чтобы создать романтичный, более сдержанный образ, уложите слои супер гладко. А вот намеренно растрепанные волосы, словно вы только что подняли голову с подушки, придадут вам более расслабленный, беззаботный и молодежный вид.

Вывод.

Таким образом, мы выявили взаимосвязь предмета математики и профессии парикмахера. Обозначили математические термины, встречающиеся в спец. предмете. Рассмотрели различные виды причесок и стрижек, связанных с геометрическими фигурами.
   В нашем исследовании мы ответили на такие высказывания: «Зачем нужно изучать математику, знать свойства функций, решать задачи».

Изучение математики развивает логическое мышление, приучает человека к точности, к умению видеть главное, сообщает необходимые сведения для понимания сложных задач.

Список литературы

1.     Math24.ru  Формулы и Таблицы - http://www.math24.ru/hyperbola-and-parabola.html

2.     Егэ по математике  -   http://uztest.ru/abstracts/?idabstract=970472

3.     Айдос Е.Ж. http://www.rusnauka.com/6_NITSB_2010/Pedagogica/58434.doc.htm

4.     Марселина.ru (ЖЖ)  http://marselina.ru/publications/4050/

5.     Свадебные прически.  http://hairandwedding.ru/rococo.html

6.     Мечтательница http://everdream.ru/forum/index.php?topic=4689.15

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru