ИТЕРАЦИОННЫЕ СТРУКТУРЫ.docx

ИТЕРАЦИОННЫЕ СТРУКТУРЫ

Теперь нашей задачей является изучение некоторых повторяющихся структур, используемых при описании алгоритми- ческих процессов. В этом разделе мы обсудим итерационные структуры, в которых выполнение набора инструкций повторя- ется в циклическом режиме. В следующем разделе рассматривается метод рекурсии. Читатель также сможет познакомиться с некоторыми популярными алгоритмами – последовательного и двоичного поиска, а также с алгоритмом сортировки мето- дом вставки. Начнем с рассмотрения алгоритма последовательного поиска.

Алгоритм последовательного поиска. Рассмотрим задачу поиска в списке некоторого заданного значения. Необходи- мо разработать алгоритм, позволяющий установить, есть ли заданное значение в списке. Если это значение в списке присут- ствует, поиск будет считаться успешным, в противном случае будем считать его завершившимся неудачей. Будем считать, что список отсортирован согласно некоторому правилу, позволяющему упорядочить его элементы. Например, если это спи- сок имен, будем считать, что имена в нем расположены в алфавитном порядке. Если же это список числовых значений, бу- дем полагать, что его элементы расположены в порядке возрастания.

Давайте попробуем представить, как бы мы действовали при поиске определенного имени в списке гостей, содержащем около 20 фамилий. В данном случае можно было бы просмотреть весь список от начала и до конца, сравнивая каждый его элемент с искомым именем. Если требуемое имя будет найдено, поиск завершится успешно. Однако, если будет достигнут конец списка или обнаружено имя, расположенное по алфавиту после искомого, поиск завершится неудачей. (Не забывайте, что список упорядочен в алфавитном порядке, поэтому если будет найдено имя, расположенное по алфавиту после требуе- мого, то это означает, что нужного нам имени в списке нет.) Таким образом, наша задача – выполнять последовательный просмотр элементов списка в направлении сверху вниз до тех пор, пока не будут проверены все имена или нужное нам имя не будет найдено.

С помощью нашего псевдокода этот процесс можно представить следующим образом: Выбрать в качестве ПроверяемоеЗначение первый элемент Списка; while (ИскомоеЗначение > ПроверяемоеЗначение

и есть непроверенные элементы) do

{выбрать в качестве ПроверяемоеЗначение следующий элемент Списка}

По окончании выполнения структуры while искомое значение либо будет найдено, либо выяснится, что его нет в спи- ске. В любом случае успешность поиска можно установить, сравнивая искомое значение с проверяемым. Если они эквива- лентны, поиск успешен. Таким образом, в конец приведенной выше программы необходимо добавить следующую инструк- цию:

if (ИскомоеЗначение = ПроверяемоеЗначение)

then {сообщить об успехе}

else {сообщить о неудаче}

Наконец, в нашей программе предполагается, что первая инструкция, где в качестве проверяемого значения явно указан первый элемент списка, содержит, как минимум, один элемент. Конечно же, это условие могло бы выполняться всегда, од- нако для полной уверенности в правильности программы следует поместить составленную выше программу в предложение else следующей инструкции if:

if (Список пуст)

then {сообщить о неудаче}

else {...}

В результате получается процедура, текст которой приведен на рис. 4.6. Заметим, что для поиска некоторых значений в списке другие процедуры вполне могут использовать ее с помощью следующей инструкции:

Применить процедуру Поиск к списку пассажиров, чтобы найти имя "Даррел Бейкер"

Эта инструкция позволяет установить, является ли Даррел Бейкер пассажиром некоторого рейса. Вот еще один пример:

Рис. 4.6. Алгоритм последовательного поиска, записанный с помощью псевдокода

Применить процедуру Поиск к списку ингредиентов, используя в качестве искомого значе- ния "мускатный орех"

Данная инструкция позволит установить, входит ли мускатный орех в перечень ингредиентов некоторого блюда.

Итак, можно сказать, что представленный на рис. 4.6 алгоритм последовательно рассматривает все элементы списка. По этой причине данный алгоритм называется алгоритмом последовательного поиска (sequential search). В силу своей простоты он часто применяется к коротким спискам либо, когда это необходимо, по каким-то иным соображениям. Однако в случае длинных списков этот метод оказывается менее эффективным, чем другие (в чем мы скоро убедимся).

Управление циклами. Неоднократное использование инструкции

или последовательности инструкций представляет собой важную алгоритмическую концепцию. Одним из методов органи- зации такого повторения является итеративная структура, известная как цикл (loop); здесь последовательность инструкций, называемая телом цикла, многократно выполняется под контролем некоторого управляющего процесса. Типичный пример цикла можно найти в алгоритме последовательного поиска, представленном на рис. 4.6. Здесь инструкция while используется в целях управления повторным выполнением единственной инструкции "выбрать следующий элемент списка как Проверяе- мое_значение". Общий синтаксис инструкции while имеет такой вид:

while (условие) do {тело цикла}

Эта инструкция представляет собой типичный образец циклической структуры, т.е. при ее выполнении циклически со- вершаются следующие действия:

проверить условие выполнить тело цикла проверить условие выполнить тело цикла

.

.

.

проверить условие

Эти действия будут продолжаться до тех пор, пока заданное условие будет выполняться.

Как правило, использование циклических структур придает алгоритму большую гибкость по сравнению с явным мно- гократным написанием тела цикла. Рассмотрим такой пример:

Выполнить инструкцию "Добавить каплю серной кислоты" три раза.

Эта циклическая структура эквивалентна такой последовательности инструкций:

Добавить каплю серной кислоты. Добавить каплю серной кислоты. Добавить каплю серной кислоты.

Однако невозможно написать аналогичную последовательность, эквивалентную следующему циклу:

while (уровень рН больше, чем 4) do {добавить каплю серной кислоты}

Суть в том, что мы не знаем заранее, сколько капель серной кислоты понадобится в каждом конкретном случае.

А теперь давайте подробно рассмотрим, как осуществляется управление циклом. Может показаться, что эта часть структуры цикла менее важна. Ведь именно в теле цикла непосредственно выполняются требуемые действия (например, до- бавляются капли кислоты). Поэтому управляющие действия можно рассматривать просто как надстройку, появившуюся только из-за того, что мы решили повторять выполнение тела цикла. Однако опыт показывает, что именно управление цик- лом чаще всего служит источником ошибок в циклических структурах и, следовательно, требует особого внимания.

Управление циклом состоит из трех операций: инициализации, проверки и модификации (рис. 4.7), причем все они обя- зательны для успешного управления циклом. Назначение операции проверки состоит в обеспечении своевременного оконча- ния циклического процесса за счет отслеживания возникновения условия, указывающего, что цикл пора заканчивать. Это условие называют условием завершения цикла. Именно для выполнения операции проверки некоторое условие обязательно указывается при записи каждой инструкции while нашего

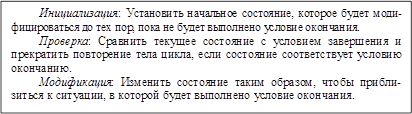
Рис. 4.7. Операции управления циклом

псевдокода. Однако условие, задаваемое в инструкции while, – это условие продолжения цикла, а условие завершения – это отрицание условия, заданного в инструкции while. Поэтому в инструкции while показанной на рис. 4.6, условие завершения выглядит следующим образом:

(Искомое_Значение ≤ Проверяемое_Значение) или (больше нет не рассмотренных элементов)

Остальные две операции управления циклом гарантируют, что условие завершения обязательно возникнет. Операция инициализации устанавливает начальное состояние, а операция модификации изменяет его в направлении достижения условия завершения. Например, на рис. 4.6 операция инициализации выполняется инструкцией, предшествующей инструкции while. В этой операции первый элемент списка устанавливается в качестве текущего проверяемого. Операция модификации в этом случае реализуется в теле цикла, когда интересующая нас позиция (проверяемый элемент) перемещается к концу списка. Таким образом, выполнение операции инициализации и многократное выполнение операции модификации приводят к тому, что условие завершения обязательно будет достигнуто. (Или обнаружится проверяемый элемент, больший либо равный ис- комому, или будет достигнут конец списка.)

Следует подчеркнуть, что операции инициализации и модификации обязательно должны приводить к заданному усло- вию завершения. Это является важнейшим требованием организации надлежащего управления циклом, поэтому при разра- ботке циклической структуры следует, как минимум, дважды убедиться в том, что оно выполняется. Если пренебречь по- добной проверкой, то это может привести к ошибкам даже в простейших случаях. Типичным примером могут служить сле- дующие инструкции:

Число ← 1

while (Число ≠ 6) do {Число ← Число + 2}

В данном случае условием завершения является выражение Число ≠ 6. Однако переменная Число инициализируется значе- нием 1, а затем увеличивается на 2 на каждом этапе модификации. Таким образом, при выполнении цикла переменной Число будут присваиваться значения 1, 3, 5, 7, 9, ... и ее значение никогда не будет равно 6. В результате выполнение данного цикла никогда не закончится.

Существуют два варианта широко распространенных циклических структур, которые отличаются только порядком вы- полнения операций управления циклом. Первая представлена инструкцией нашего псевдокода:

while (условие) do {действие}

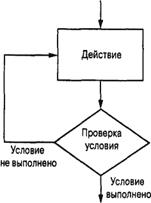
Семантика этой циклической структуры представлена на рис. 4.8 в виде блок-схемы. На подобных схемах для представ- ления отдельных этапов выполнения используются различные геометрические фигуры, а стрелки указывают порядок вы- полнения этих этапов. Различные фигуры отражают отдельные типы деятельности, выполняемой на соответствующем этапе. Ромб указывает на принятие решения, а прямоугольник представляет произвольную инструкцию или последовательность инструкций. Обратите внимание, что в данной циклической структуре проверка условия завершения производится до того, как выполняется тело цикла.

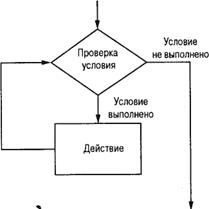
В противоположность этому, в структуре, представленной на рис. 4.9, указывается, что тело цикла должно выполняться до проверки условия завершения. В результате тело цикла всегда выполняется хотя бы один раз, в то время как в структуре ти- па while тело цикла может не выполниться ни разу (если условие завершения будет выполнено при первой же его провер- ке).

В нашем псевдокоде общий синтаксис цикла этого типа имеет следующий вид:

Рис. 4.8. Блок-схема цикла

while-do

Рис. 4.9. Блок-схема цикла

repeat-until

Рассмотрим конкретный пример:

repeat {взять монету из кармана} until (в кармане нет монет)

Когда выполнение алгоритма доходит до этой инструкции, подразумевается, что в кармане есть хотя бы одна монета. Это предположение не является обязательным при использовании следующей инструкции:

while (в кармане есть монета) do {взять монету из кармана}

Придерживаясь терминологии нашего псевдокода, будем называть эти структуры оператором цикла с условием про- должения и оператором цикла с условием завершения. Иногда оператор цикла while называют априорным циклом (pretest loop), или циклом с предусловием, поскольку условие завершения проверяется до выполнения тела цикла, а оператор цикла repeat называется апостериорным циклом (posttest loop), или циклом с постусловием, поскольку условие завершения про- веряется после выполнения цикла.

Алгоритм сортировки методом вставки. В качестве дополнительного примера итеративной структуры рассмотрим задачу сортировки списка имен в алфавитном порядке. Прежде чем приступить к обсуждению, следует установить некото- рые ограничения, которые необходимо будет учитывать. Попросту говоря, наша задача – отсортировать список "внутри его самого". Другими словами, мы хотим отсортировать список, просто переставляя его элементы, а не перемещая весь список в другое место. Это аналогично сортировке списка, элементы которого записаны на отдельных карточках, разложенных на переполненном рабочем столе. На столе достаточно места для всех карточек, однако запрещается отодвигать другие нахо- дящиеся на столе материалы, чтобы освободить дополнительное пространство. Подобное ограничение типично для компью- терных приложений, но не потому, что рабочее пространство в машине обязательно переполнено, как наш рабочий стол, а потому, что мы стремимся использовать доступный объем памяти самым эффективным образом. Попробуем сделать первый шаг в поисках решения задачи. Рассмотрим, как можно было бы отсортировать карточки с именами, расположенные на ра- бочем столе. Пусть исходный список имен выглядит следующим образом:

Fred Alice David Bill Carol

Один из подходов к сортировке этого списка заключается в следующем. Обратите внимание, что подсписок, состоящий из единственного верхнего имени Fred, уже отсортирован, а подсписок из двух верхних имен, Fred и Alice, – еще нет. Поэто- му подымем карточку с именем Alice, поместим карточку с именем Fred вниз, туда, где раньше была карточка с именем Alice, а затем положим карточку с именем Alice в самое верхнее положение, как показано в первой строке на рис. 4.10. Те- перь список будет иметь такой вид:

Alice Fred David Bill Carol

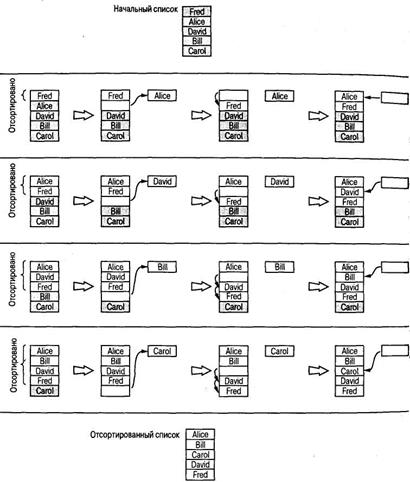
Рис. 4.10. Сортировка списка имен Fred, Alice, David, Bill и Carol

В этом варианте два верхних имени образуют отсортированный подсписок, а три верхних – нет. Подымем третью кар- точку с именем David, опустим карточку с именем Fred вниз, туда, где только что была карточка с именем David, а затем по- местим карточку с именем David в ту позицию, которую раньше занимала карточка с именем Fred, как показано во второй строке на рис. 4.10. Теперь три верхних элемента списка образуют отсортированный подсписок. Продолжая действовать та- ким способом, мы можем получить список, в котором будут отсортированы четыре верхних элемента. Для этого нужно под- нять четвертую карточку с именем Bill, опустить вниз карточки с именами Fred и David, а затем поместим карточку с именем Bill в освободившуюся позицию (третья строка на рис. 4.10). И наконец, чтобы завершить процесс сортировки, необходимо поднять карточку с именем Carol, опустить вниз карточки с именами Fred и David, а затем поместить карточку с именем Carol в освободившуюся позицию – как показано в четвертой строке на рис. 4.10.

Теперь наша задача состоит в том, чтобы проанализировать процесс сортировки конкретного списка и попытаться обобщить его в целях получения алгоритма сортировки любого списка. С этой точки зрения каждая строка на рис. 4.10 пред- ставляет собой один и тот же повторяющийся процесс: "Поднять карточку с именем, первую в неотсортированной части списка, сдвинуть вниз карточки с именами, которые находятся ниже по алфавиту, чем имя на взятой нами карточке, а затем поместить эту взятую карточку на освободившееся место в списке". Если назвать выбранное имя опорным элементом, то с помощью нашего псевдокода данный процесс можно описать следующим образом:

Переместить ОпорныйЭлемент во временное хранилище, оставив в списке пустое место;

while (над пустым местом есть имя, и оно > ОпорныйЭлемент) do

{переместить имя, находящееся над пустым местом, вниз, оставив в его прежней позиции пустое место}

Поместить ОпорныйЭлемент на пустое место в списке

Обратите внимание, что этот процесс должен выполняться многократно. Чтобы начать процедуру сортировки, в качест- ве опорного элемента должен быть выбран второй элемент списка. Затем, перед каждым последующим выполнением опи- санной процедуры, должен выбираться новый опорный элемент, находящийся на одну позицию ниже предыдущего, и так до тех пор, пока не будет достигнут конец списка, т.е. положение опорного элемента должно перемещаться от второго элемента к третьему, затем к четвертому и т.д. Следуя этому, мы можем организовать требуемое управление путем повторения проце- дуры с помощью следующей последовательности инструкций:

N ← 2;

while (N ≤ ДлинаСписка) do

{выбрать N-й элемент как ОпорныйЭлемент;

.

.

.

N ← N + 1}

Здесь N – счетчик, параметр ДлинаСписка – количество элементов в списке, а точки указывают место, где должна располагаться составленная нами выше процедура.

Полный текст программы сортировки на языке псевдокода приведен на рис. 4.11. Не вдаваясь в подробности, можно сказать, что эта программа сортирует список, многократно повторяя следующие действия: "Элемент извлекается из списка, а затем вставляется на надлежащее ему место". Именно по причине многократного повторения вставки элементов в список данный алгоритм получил название сортировки методом вставки (insertion sort).

Обратите внимание, что представленная на рис. 4.11 структура содержит Цикл, помещенный внутрь другого цикла. Внешний цикл представлен первой инструкцией while, а внутренний цикл – второй инструкцией while. Каждое выполне- ние тела внешнего цикла приводит к тому, что внутренний цикл инициализируется и выполняется до тех пор, пока не будет выполнено условие его окончания. Таким образом, однократное выполнение тела внешнего цикла будет сопровождаться многократным выполнением тела внутреннего цикла.

ции

Рис. 4.11. Алгоритм сортировки методом вставки, написанный на псевдокоде

При инициализации управления внешним циклом начальное значение счетчика N устанавливается с помощью инструк-

N ← 2;

Операция модификации этого цикла включает увеличение значения счетчика N в конце тела цикла с помощью инст-

рукции

N ← N + 1.

Условие окончания внешнего цикла выполняется, когда значение счетчика N превысит длину сортируемого списка.

Управление внутренним циклом инициализируется, когда опорный элемент извлекается из списка и в нем образуется пустое место. Операция модификации включает перемещение расположенных выше элементов на пустое место вниз, в ре- зультате чего свободное место перемещается вверх по списку. Условие окончания выполняется, когда пустое место или на- ходится непосредственно под именем, которое по алфавиту размещается выше опорного значения, или же достигает верхней позиции списка.

Вопросы для самопроверки

1.     Преобразуйте показанную на рис. 4.6 процедуру последовательного поиска так, чтобы она могла работать с неот- сортированными списками.

2.     Перепишите приведенную ниже программу на псевдокоде так, чтобы в ней использовались повторяющиеся инструкции

repeat-until.

Z ← 0;

X ← 1;

while (X < 6) do

{Z ← Z + X;

X ← X + 1}

3.     Предположим, что процедура сортировки методом вставки, представленная на рис 4.11, была применена к списку George, Cheryl, Alice и Bob. Опишите, как будет выглядеть список каждый раз по окончании выполнения тела внешней структуры while.

4.     Почему не следует заменять фразу "по алфавиту размещается ниже" в инструкции while на рис. 4.11 на фразу "по алфавиту размещается ниже или эквивалентно"?

5.     Вариантом алгоритма сортировки методом вставки является выборочная сортировка (selection sort). Каждый раз вы- бирается наименьший элемент списка и помещается на первое место. Затем выбирается наименьший элемент из оставшихся элементов списка и помещается на второе место в списке. Многократно выбирая наименьший элемент из оставшейся части списка и перемещая его вперед, мы увеличиваем отсортированную часть списка, находящуюся вначале, тогда как его конеч- ная часть, состоящая из неотсортированных элементов, сжимается. С помощью нашего псевдокода напишите процедуру сортировки списка с использованием алгоритма выборочной сортировки, аналогичную процедуре, представленной на рис. 4.11.

6.     Другой известный алгоритм сортировки – сортировка методом пузырька (bubble sort). Он основан на процессе по-

вторяющегося сравнения двух стоящих рядом имен и перестановки их местами, если они находились относительно друг

друга в порядке, отличном от требуемого. Предположим, что сортируемый список состоит из n элементов. Сортировка мето- дом пузырька начнется сравнением (и, возможно, перестановкой) элементов, стоящих на местах n и n – 1. Затем сравни- ваются элементы, стоящие на местах n – 1 и n – 2, и так далее в направлении к началу списка, пока не будет выполнено срав- нение (и, возможно, перестановка) первого и второго элементов списка. В результате прохождения по всему списку его наи- меньший элемент будет вынесен на первое место. Аналогичным образом, после второго прохождения списка следующий по величине элемент будет вынесен на второе место и т.д. Таким образом, пройдя список n – 1 раз, мы отсортируем его цели- ком. (Если визуально представить себе работу данного алгоритма, то создается впечатление, что наименьшие из оставшихся неупорядоченных элементов списка последовательно всплывают к его вершине как пузырьки, – отсюда и название алгорит- ма.) Используя наш псевдокод, напишите процедуру сортировки списка методом пузырька по аналогии с процедурой, пред- ставленной на рис. 4.11.