Поделиться
Задача по программированию Решить квадратное уравнение.docx
Формулировка. Даны вещественные числа a, b и c, причем a отлично от 0. Решить квадратное уравнение ax2 + bx + c = 0 или сообщить о том, что действительных решений нет.
Решение. Из алгебры известно, что:
Квадратное уравнение ax2 + bx + c = 0, выражение D = b2 – 4ac – дискриминант:
– если D > 0, имеет
два решения: 
,
;
– если D = 0, имеет
единственное решение: 
;
– если D < 0, не имеет действительных решений.
Следовательно, нам необходимо вычислить дискриминант (заведем для него вещественную переменную d типа real) и в зависимости от его значения организовать ветвления. Сначала нужно проверить, имеет ли уравнение действительные решения (для решений заведем переменные x1 и x2 типа real). Если да, и если дискриминант не равен нулю, то вычисляем оба решения по формулам, а если дискриминант равен нулю, то вычисляем единственное решение. Если же действительных решений нет, выводим текстовое сообщение об этом. Основной алгоритм можно проиллюстрировать следующей блок-схемой:
 |
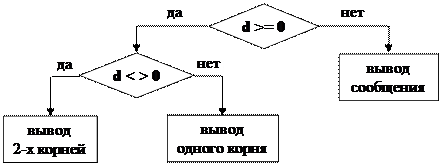Три нерасшифрованных блока представляют собой стандартные операторы вывода. Разберем их подробнее:
1) При выводе двух корней выражение будет выглядеть следующим образом:
x1 := (-b + sqrt(d)) / 2 * a;
x2 := (-b - sqrt(d)) / 2 * a;
writeln('x1 = ', x1:4:2, ', x2 = ', x2:4:2);
При этом выводимое выражение будет выглядеть так: 'x1 = m, x2 = n', где синим цветом выделены однозначные текстовые константы, которые берутся из списка аргументов writeln, красным – вычисленные значения x1 и x2. Причем корни выведены в форматированном виде: число после первого двоеточия задает ширину поля вывода для переменной вместе с точкой (при нехватке поля она будет расширено программой), а число после второго двоеточия – количество выводимых дробных знаков (его при работе программы изменить нельзя);
2) При выводе одного корня – все то же самое, только выводится один корень:
x1 := -(b / 2 * a);
writeln('x = ', x1:4:2);
3) При отсутствии действительных корней выводим сообщение:
writeln('No real solutions!');
В итоге внутренний условный оператор с телом включительно будет выглядеть так:
if d <> 0 then begin
x1 := (-b + sqrt(d)) / 2 * a;
x2 := (-b - sqrt(d)) / 2 * a;
writeln('x1 = ', x1:4:2, ', x2 = ', x2:4:2)
end
else begin
x1 := -(b / 2 * a);
writeln('x = ', x1:4:2)
end;
Код:
|
1. program QuadraticEquation; 2. 3. var 4. a, b, c, d, x1, x2: real; 5. 6. begin 7. readln(a, b, c); 8. d := b * b - 4 * a * c; 9. if d >= 0 then begin 10. if d <> 0 then begin 11. x1 := (-b + sqrt(d)) / 2 * a; 12. x2 := (-b - sqrt(d)) / 2 * a; 13. writeln('x1 = ', x1:4:2, ', x2 = ', x2:4:2) 14. end 15. else begin 16. x1 := -(b / 2 * a); 17. writeln('x = ', x1:4:2) 18. end 19. end 20. else begin 21. writeln('No real solutions!'); 22. end 23. end. |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
