«Как научить моделировать реальные ситуации на языке геометрии? Использование свойств геометрических фигур для решения

Выступление на ГМО учителей математики г.Оренбурга

учителя МОАУ « СОШ №62» Яковлевой Т.Л.

Тема: «Как научить моделировать реальные ситуации на языке геометрии? Использование свойств геометрических фигур для решения задач практического содержания».

«Математике должно учить еще с той целью, чтобы познания

здесь приобретаемые, были достаточными для обыкновенных потребностей жизни.»

Н. И. Лобачевский

Каждому человеку в своей жизни приходится выполнять математические

расчеты, пользоваться вычислительной техникой, находить в справочниках нужные формулы, владеть приемами геометрических измерений, читать информацию, представленную в виде таблиц, диаграмм, графиков.

В ФГОС одним из основных требований к усвоению знаний учащихся является умение применять полученные знания в реальных жизненных ситуациях.

Требование ФГОС: подготовить выпускника, обладающего необходимым набором современных знаний, умений и качеств, позволяющих ему уверенно чувствовать себя в самостоятельной жизни, умеющего применять знания в реальных ситуациях.

Поэтому в настоящее время важно не заучивание теории, а способность

применять знания на практике. Реализовать данное требование ФГОС на уроках математики помогают практико- ориентированные задачи.

Практико - ориентированная задача позволяет обучать школьников решать

жизненные проблемы с помощью предметных знаний.

Практико – ориентированная задача повышает интерес к предмету,

способствует развитию любознательности и творческой активности.

При решении таких задач дети сами ищут, сопоставляют, обобщают, делают

выводы – одним словом действуют.

В процессе математической деятельности в арсенале приемов и методов

человеческого мышления естественным образом включается индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление.

Именно решение задач ведет к развитию способности самостоятельно и

логически мыслить, учит строить математические модели реальных ситуаций, возникающих при практической трудовой деятельности людей. Решение задач – основной вид деятельности на уроках математики и, поэтому, интересное содержание задач делает актуальными для учащихся математические знания.

Для решения практико - ориентированных задач важно развить у учеников умение моделировать реальные ситуации на языке геометрии, использовать свойства геометрических фигур.

Конечно, на каждом уроке геометрии нет возможности решать такие задачи Поэтому я предлагаю свой вариант применения практико- ориентированных задач при изучении некоторых тем геометрии в 7, 8 классах , а так же тем алгебры 7 класса.

Изучая тему " Формулы сокращенного умножения " в алгебре 7 класса можно показать детям наряду с алгебраическим выводом формул их геометрическое доказательство:

1. Квадрат суммы.

Вывод формулы (a+b)²= a² + 2ab + b²

Построим квадрат со стороной a+b, проведя внутри него отрезки, соединяющие границы отрезков a и b на каждой из сторон.

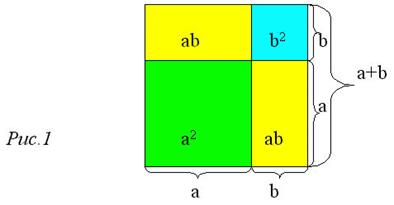
Полученный чертеж настолько прозрачен, что хочется просто написать, как писали древнегреческие геометры: «Смотри!» – и более ничего. Площадь квадрата со стороной a+b состоит из площади квадрата со стороной a, площади квадрата со стороной b и двух прямоугольников с площадями ab. То есть она равна a² + b²+ 2ab, или a² + 2ab + b². Алгебраическое доказательство сложнее и не столь наглядно.

2. Разность квадратов.

Вывод формулы (a² – b²) = (a– b)(a + b). Строим квадрат со стороной a, внутри него квадрат со стороной b (если b<a), проводим внутри отрезок, как показано на рис.2.

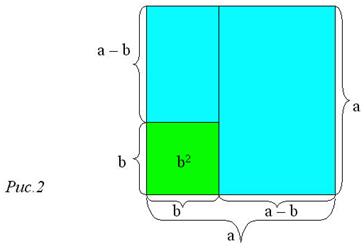
Мы видим, что разность площадей квадратов равна площади двух прямоугольников – большого и малого. Переместив малый прямоугольник так, чтобы равные стороны прямоугольников совместились (см. рис.3),

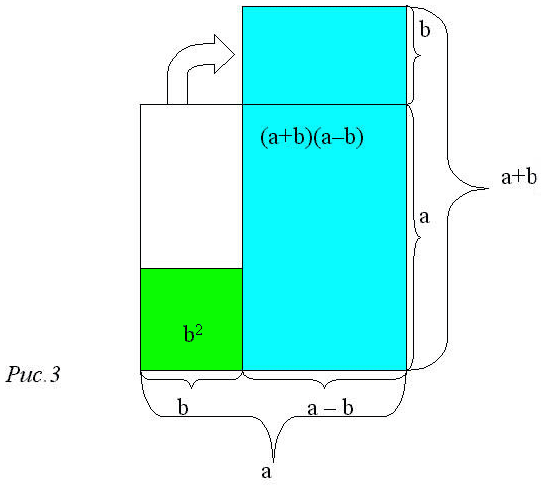
получим прямоугольник со сторонами (a – b) и (a + b). Следовательно, разность площадей квадратов равна (a – b)(a + b), что и требовалось доказать.

Такие геометрические доказательства есть для всех формул сокращенного умножения. Они имеются в учебниках. Часть из них можно рассмотреть с учениками в рамках урока, часть предложить ученикам для подготовки выступления.

Несомненно, моделировать реальные ситуации на языке геометрии чаще приходиться на уроках геометрии. В УМК практико- ориентированные задачи есть, например в темах" Практические приложения подобных треугольников", "Соотношения между сторонами и углами прямоугольного треугольника", но для того, чтобы сформировать навыки моделировать реальные ситуации на языке геометрии их не достаточно. Но если посмотреть на материалы ВПР по математике 8 класса, то в распределение заданий по позициям кодификаторов в ВПР выделены умения, виды деятельности (в соответствии с ФГОС):

для №15-развитие умений моделировать реальные ситуации на языке геометрии, исследовать построенную модель с использованием геометрических понятий и теорем, аппарата алгебры.

Вот эти здания считаю целесообразным разбирать при изучении тем, теоретические знания которых необходимы для выполнения задания ВПР. Кроме сборников для подготовки к ВПР их большое количество на сайте

" Сдам ГИА: решу ВПР. Математика 8 класс

https://math8-vpr.sdamgia.ru

Приведу примеры соответствия задания ВПР и учебных тем.

№п/п	Задача ВПР №15	Класс, тема в программе.
1	Демоверсия ВПР -2022	8 класс. Теорема Пифагора
2		7 класс. Признаки равенства прямоугольных треугольников
3		8класс. Пропорцион альные отрезки или о подобии произвольных фигур.
4	Решу ВПР 8 класс Конструкторы горки на детской площадке получали слишком много жалоб на горку DCB. Её называли слишком экстремальной для детей и не раз просили сделать последнюю поменьше, сделав наклон не настолько крутым. Известно так же, что горка выполнена в виде прямоугольного треугольника, его гипотенуза равна 7 м. Более того, конструкторы уже составили план по уменьшению горки: согласно их расчётам, при уменьшении гипотенузы на 2 м, ее катет уменьшится на 4 м. Найдите исходные и новые значения длины и высоты горки. В ответ запишите новую высоту горки в метрах. Решение. Для решения данной задачи примем катеты за неизвестные. Пусть они равны a и b соответственно. Тогда согласно условиям задачи составим систему уравнений и решим ее, вычтя из первого уравнения второе: $система выражений a в степени 2 плюс b в степени 2 =49,(a минус 4) в степени 2 плюс b в степени 2 =25 конец системы . равносильно система выражений a в степени 2 плюс b в степени 2 =49, 8a=40 конец системы . \undersetb больше 0\mathop равносильно система выражений a=5,b=2 корень из 6 . конец системы .$ Таким образом, первоначально горка была высотой 5 м и длиной $2 корень из 6 \approx 4,9$ м. После уменьшения горки, ее параметры стали равны 1 м и 4,9 м соответственно. Ответ: 1.	8 класс. Теорема Пифагора
5	Лист жести имеет форму прямоугольника, длина которого на 10 см больше ширины. По углам этого листа вырезали квадраты со стороной 5 см и сделали коробку. Найдите размеры листа жести в сантиметрах, если объем коробки равен 1000 см³. Объем коробки равен произведению ее длины, ширины и высоты. Решение. Примем стороны прямоугольника за a см и b см. После вырезания его стороны стали равны см и см. Высота коробки — 5 см. Из условия задачи составим систему уравнений: Решим её методом подстановки: $равносильно система выражений b в степени 2 минус 10b минус 200=0,a=10 плюс b конец системы . \undersetb больше 0\mathop равносильно система выражений b=20,a=30 конец системы .$ Таким образом, ширина и длина листа жести равны 20 и 30 сантиметров соответственно.	8 класс. Площадь прямоугольника
6	Чтобы сделать витраж в виде мозаики, стекольщик режет равнобедренную трапецию на два равнобедренных треугольника. Для этого он соединяет две несмежные вершины трапеции и исполняет задуманное. Найдите углы трапеции. Ответ дайте в градусах. Решение. Рассмотрим 2 случая Первый случай:если то треугольник ABC — равнобедренный с основанием AC. Если то треугольник ADC — равнобедренный с основанием CD. Так как углы при основании равнобедренного треугольника равны, то $\angle BAC=\angle BCA,$ $\angle ADC=\angle ACD.$ Далее $\angle DAC=\angle BCA$ как внутренние накрест лежащие при и секущей AC. Пусть $\angle BAC=x,$ тогда $\angle BCA=x,$ $\angle DAC=x.$ Тогда $\angle BAD=\angle BAC плюс \angle DAC=2x.$ Тогда $\angle ADC=\angle BAD=2x$ как углы при основании равнобедренной трапеции. Следовательно, $\angle ACD=2x,$ $\angle BCD=\angle BCA плюс \angle ACD=3x.$ По свойству равнобедренной трапеции имеем $\angle BAD плюс \angle BCD=180 градусов$ Составим уравнение: Значит, $\angle BAD=2 умножить на 36=72 градусов, \angle BCD=3 умножить на 36=108 градусов.$ Второй случай: если то треугольник ABC — равнобедренный с основанием BC. Тогда у него углы при основании равны: $\angle B=\angle BCA.$ Но угол B — тупой, а два тупых угла в треугольнике быть не может. Следовательно, AB не может быть равным AC. Тогда и CD не может быть равным AC, так как по условию. Ответ: 72 и 108.	8 класс. Трапеция. Свойства равнобедренного треугольника и равнобедренной трапеции
7	В парке отдыха создали бассейн для большого и глубокого пруда, задумав его в форме идеального круга, радиус которого равен 1 км. Залив фундамент водой и создав все необходимые условия для создания микрофлоры, ответственные за проект затеяли разместить на нем две лодочные станции, чтобы все желающие могли насладиться прогулками по воде. Их решили расположить в диаметрально противоположных точках. Кроме того, планировщики подумали, что было бы неплохо создать промежуточную станцию, расстояние от которой до одной из лодочных станций в два раза больше расстояния до другой. Все расстояния рассматриваются по воде. Найдите приближенно большее расстояние от промежуточной станции до лодочной станции в метрах, считая, что Решение. Задача сводится к нахождению большего катета в прямоугольном треугольнике, гипотенуза которого известна. Пусть неизвестный катет равен x км. Тогда второй катет равен 2x. По теореме Пифагора находим катет Откуда получаем, что Подставляя значение 2,24 вместо получаем: $x\approx2 умножить на дробь: числитель: 2,24, знаменатель: 5 конец дроби =0,896.$ Итак, длина катета равна приблизительно 0,896 км, то есть 896 м. Тогда длина большего катета равна 1792 м. Ответ: 1792.	8 класс. Теорема о вписанном угле Следствие из теоремы о вписанном угле.
8	Столяр вырезал полку для шкафа в виде пятиугольника, в основе — квадрат 300 × 300 мм, от которого отрезан один угол (см. рисунок) так, что длина скошенной кромки равна 180 мм. Теперь столяру нужно вырезать похожую полку, у которой три кромки выдаются на 25 мм по сравнению с первой полкой. Какова будет длина скошенной кромки у второй полки? Считайте $тангенс 22,5 градусов \approx 0,4142.$ Результат округлите до целого числа миллиметров. Запишите решение и ответ. Решение. Соединим отрезком вершины соответствующих тупых углов вырезанной полки и новой полки. Проведём перпендикуляры из вершины вырезанной полки к кромке проектируемой полки, как показано на рисунке. Обозначим полученные прямоугольные треугольники ABC и ADC. Луч CA является биссектрисой угла BCD проектируемой полки. Значит, угол ACB равен 67,5° и поэтому $\angle BAC=22,5 градусов.$ Тогда Скошенная кромка новой полки длиннее, чем скошенная кромка старой, на удвоенную длину отрезка BC: $180 плюс 2 умножить на 25 умножить на тангенс 22,5 градусов\approx 200,71\approx 201мм.$ Ответ: 201 мм.	8 класс. Синус, косинус и тангенс острого угла прямоугольного треугольника
9	КИМ ОГЭ На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка. Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию. 1.Найдите площадь санузла. Ответ дайте в квадратных метрах. 2.Найдите площадь коридора. Ответ дайте в квадратных метрах. 3. Найдите площадь большей лоджии. Ответ дайте в квадратных метрах. 4. Найдите площадь кухни. Ответ дайте в квадратных метрах. 5. Паркетная доска размером 20 см на 40 см продаётся в упаковках по 8 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол коридора? 6. Плитка для пола размером 40 см на 40 см продаётся в упаковках по 12 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол кухни?	8 класс. Площадь прямоугольника

Далее приведу примеры из открытого банка заданий по формированию математической грамотности, это задание для 9 класса, но рассматривать решение можно в 7,8 классах:

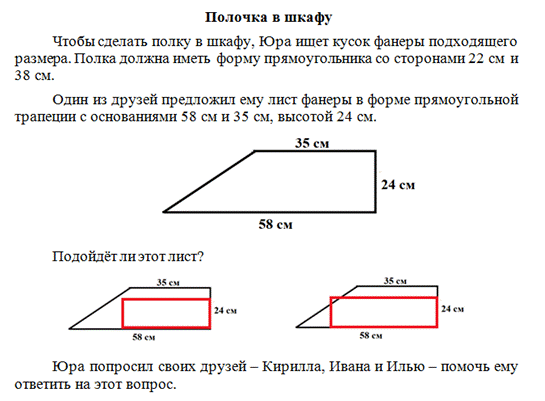
В задании №1описан один из классических сюжетов измерений на местности – определение ширины реки. Приводится алгоритм построений на местности с соответствующим ему чертежом. Способ основан на построении двух равных треугольников.

В задании требуется обосновать приведенный алгоритм, то есть привести доказательство того, что построенный отрезок равен ширине реки, которое сводится ко второму признаку равенства прямоугольных треугольников по катету и прилежащему к этому катету углу. Это задание можно рассмотреть с учениками 7 класса при изучении соответствующей темы.

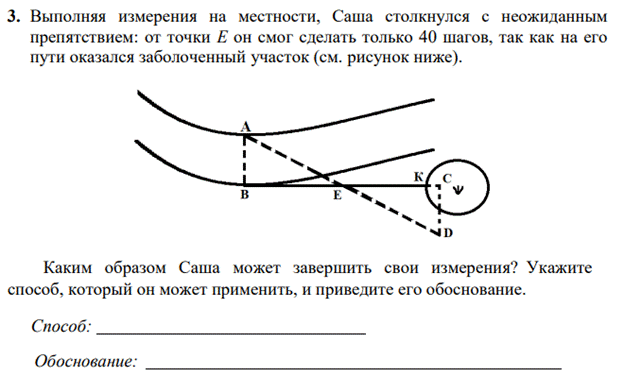
Задание №3: здесь для выполнения требуется привлечение таких фактов геометрии как подобия или симметрии. Его можно рассмотреть в 8 классе

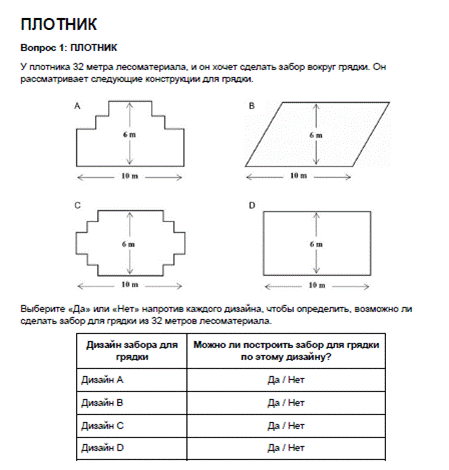
В данном задании ученики должны знать как находить периметр многоугольника, его целесообразно предложить ученикам 8 класса при решении задач по теме" Многоугольник"

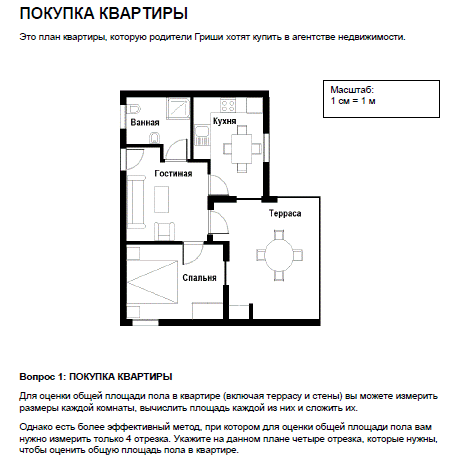
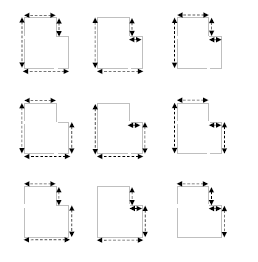
Это

Это задание можно рассмотреть как с учениками 5 класса, так и с учениками 8 класса при изучении темы" Площадь прямоугольника.

Далее приведу

ЗАДАЧИ ПО ПЛАНИМЕТРИИ

С ПРАКТИЧЕСКИМ СОДЕРЖАНИЕМ

для 7 класса

Измерение отрезков

1. Рабочие на одной стороне железнодорожной линии устанавливают телеграфные столбы через каждые 50 м. Сколько потребуется столбов, чтобы установить их на участке пути длиной 8 км? (Первый и последний столбы установлены на концах участка пути)

2. Автопоезд длиной 20 м проезжает мимо километрового столба за 10 с. Сколько времени ему понадобится для того, чтобы проехать мост длиной 40 м?

3. Сколькими способами из стержней длиной 7 и 12 см можно составить стержень длиной 1 м?

Измерение углов

1. Какой угол образуют часовая и минутная стрелки часов, когда они показывают 13 ч? 18 ч? 12 ч?

2. Найти угол между стрелками часов, если они показывают 15 ч; 9 ч; 18 ч 15 мин.; 9 ч 15 мин.

3. Сцеплены два зубчатых колеса, имеющие 30 и 48 зубьев. На какой угол повернется первое колесо, когда второе повернется на 12 зубьев? На какой угол повернется второе колесо, когда первое сделает полный оборот?

4. В результате повышения давления на 10⁵ Па стрелка манометра отклоняется вправо, описывая угол, равный 6° (отклонение стрелки прямо пропорционально изменению давления). Какой угол опишет стрелка манометра при увеличении давления на 8∙10⁵ Па?

Равенство треугольников

1. От оконного стекла треугольной формы откололся один из его уголков. Можно ли по сохранившейся части заказать стекольщику вырезать такое же оконное стекло? Какие следует снять размеры?

2. Столяру нужно заделать отверстие треугольной формы. Сколько размеров и какие он должен снять, чтобы изготовить латку? Что он должен измерить, если отверстие имеет форму: а) прямоугольного треугольника; б) равностороннего треугольника?

3. От пункта А, расположенного на берегу, к пункту В, лежащему на острове, требуется провести телефонную связь. Как, не переплывая на остров, определить необходимое количество (длину) телефонного кабеля? Какой признак равенства треугольников здесь можно использовать? (Пункты А и В расположены на берегах, а кабель прокладывается по дну реки, т. е. условно ищем длину отрезка АВ).

4. В школьной мастерской сделали из проволоки четыре стержня длиной 4, 7, 10 и 13 см. Соединяя концами три стержня из четырех, выяснить, из каких трех стержней можно составить треугольник, а из каких нельзя. Объяснить выводы.

5. При постройке кровель, мостов, подъемных кранов скрепляют опорные брусья или балки так, чтобы они образовывали систему треугольников. Почему такое расположение балок лучше обеспечивает жесткость формы сооружения, нежели иное?

Параллельные прямые. Признаки параллельности прямых

1. В городе 10 улиц параллельны друг другу, а 10 других улиц пересекают их под прямым углом. Какое наименьшее число поворотов может иметь замкнутый маршрут, проходящий через все перекрестки?

Сумма углов треугольника

1. Как измерить изображенный на доске угол, часть которого вместе с вершиной случайно стерли?

2. Два пункта А и В находятся на противоположных берегах озера. Как найти расстояние между ними, выполнив такое построение, чтобы отрезок АВ оказался одной из боковых сторон равнобедренного треугольника?

3. Угол между стропильными ногами черепичной крыши составляет 90°. Вычислить высоту крыши, если расстояние между концами стропильных ног равно 12 м.

Прямоугольный треугольник

1. Угол между стропильными ногами железной крыши обычно составляет 120°. Найти длину стропила, если его верхний конец отстоит от основания на 2,5 м.

2. При разведке бурением по рудной жиле пройдено 1,5 м. Найти мощность этой жилы, если угол падения ее равен 60°. (Мощностью жилы называют толщину пласта).

3. Железный прут длиной l изогнут в двух точках, делящих его на три равные части под углами 120° (изгиб совершался в одной плоскости и в одну сторону). Найти расстояние между концами образовавшейся скобы.

4. Из металлического стержня требуется изготовить скобу с тремя равными звеньями, образующими на сгибах угол 120°. Какой длины нужен стержень, если расстояние между концами скобы должно быть равно m?

5. Как найти высоту дерева, имея прямоугольный треугольник с углом 30°?

Геометрическое место точек

1. На полевом стане для снабжения водой трех объектов, не лежащих на одной прямой, требуется вырыть колодец, который был бы одинаково удален от всех трех объектов. Где надо выбрать место для колодца?

2. Через селение А нужно провести прямую дорогу таким образом, чтобы пункты В и С оказались на одинаковых расстояниях от этой дороги. Как это сделать?

3. На железной дороге требуется построить станцию с таким расчетом, чтобы она находилась на одинаковых расстояния од двух населенных пунктов. Где должна быть расположена станция? В каком случае такую станцию построить невозможно?

4. Два прямолинейных участка дороги нужно соединить дорогой, имеющей форму дуги окружности, так, чтобы эти участки касались построенной дуги. Как это сделать?

Итак, подведу итог: цель практико - ориентированных задач – формирование умений действовать в социально-значимой ситуации и для её успешной реализации необходимо научить моделировать реальные ситуации на языке математики.

Перед учителем математики стоит нелёгкая задача – преодолеть в сознании

обучающихся представление о «сухости», формальном характере, оторванности этой науки от жизни и практики, обеспечить органическую связь изучаемого теоретического материала с его практической значимостью.

«Нет ни одной области математики, как бы абстрактна она ни была,

которая когда-нибудь не окажется применимой к явлениям действительного мира»

Н.И. Лобачевский

Выступление на ГМО учителей математики г

Именно решение задач ведет к развитию способности самостоятельно и логически мыслить, учит строить математические модели реальных ситуаций, возникающих при практической трудовой деятельности людей

Мы видим, что разность площадей квадратов равна площади двух прямоугольников – большого и малого

Такие геометрические доказательства есть для всех формул сокращенного умножения

Теорема Пифагора 2 7 класс

Конструкторы горки на детской площадке получали слишком много жалоб на горку

Решим её методом подстановки:

Второй случай: если то треугольник

Ответ: 1792. 8 класс. Теорема о вписанном угле

КИМ ОГЭ На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме

«Как научить моделировать реальные ситуации на языке геометрии? Использование свойств геометрических фигур для решения задач практического содержания»

В задании №1описан один из классических сюжетов измерений на местности – определение ширины реки

Способ основан на построении двух равных треугольников

В данном задании ученики должны знать как находить периметр многоугольника, его целесообразно предложить ученикам 8 класса при решении задач по теме"

Это Это задание можно рассмотреть как с учениками 5 класса, так и с учениками 8 класса при изучении темы"

Измерение отрезков 1.

От оконного стекла треугольной формы откололся один из его уголков

Два пункта А и В находятся на противоположных берегах озера

Через селение А нужно провести прямую дорогу таким образом, чтобы пункты

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

12.01.2023