Как решать задачи по кинематике?

Как решать задачи по кинематике?

Ловцова Анжелика Фёдоровна.

АНО ОО "Русская Международная Школа" (г. Москва)

Не существует универсального метода решения задач по физике, но существует универсальный подход к решению задач. Когда грамотный физик, а мы собираемся стать грамотными физиками, решает задачу, то его действия можно поделить на три больших этапа:

1. Постановка задачи;

2. Решение задачи;

3. Анализ решения.

При постановке задачи и анализе решения мы являемся физиками, при решении задачи мы математики. 

Постановка задачи – наиболее важный, а в школьных задачах, и наиболее трудный этап. Мы должны понять физику явления, сформулировать физическую модель, а затем перевести ее в математическую. Конечным результатом этого этапа должна быть система уравнений и неравенств.

При решении задач по кинематике этот этап разбивается на четыре ступени:

1.Внимательно, не торопясь, прочитайте условие задачи. Подумайте, о каком физическом явлении идет речь. Какие физические величины известны, а какие надо найти? (Когда задача сложная, не следует особенно стремиться получить ответ. Надо последовательно, аккуратно ставить задачу, а ответ придет сам, куда ему деваться?)

2.Изобразите на рисунке (схематически) рассматриваемые тела, изобразите их движения.

3.Выберите систему отсчета. Для этого надо построить систему координат, т. е. задать ее начало и положительные направления координатных осей. Кроме того, надо выбрать начало отсчета времени. Без выбора системы отсчета описать движение полностью невозможно.

Для описания прямолинейного движения достаточна одна координатная ось, совмещенная с траекторией движения. Если движение происходит в одной плоскости, то потребуются две оси, для 3-х мерного движения необходима 3-х мерная система координат.

Выбор системы отсчета произволен и не влияет на конечный результат решения задачи. Но удачный выбор системы отсчета упрощает решение задачи. 

На этом мы заканчиваем построение физической модели и нам надо превратить ее в математическую модель. Помните, математика – язык физики.

4.Запишите уравнения, описывающие движения всех тел. В случае кинематики в школьных задачах это будут уравнения для зависимости координат материальных точек от времени. Далее от уравнений для значений координат и проекций заданных величин надо перейти к уравнениям для их модулей. Это непростой момент, рисунок должен Вам помочь.

5.Сформулируйте на языке математики так называемые «начальные» и «скрытые» условия. В качестве начальных условий обычно выступают значения координат и скоростей в начальный момент времени, а вот нахождение скрытых условий – это самый деликатный момент в решении задачи. В кинематике в качестве скрытых условий может быть, например, встреча двух тел в момент времени t_в, т. е. их координаты в этот момент равны. Это условие дает уравнение:

x₁(t_в) = x₂(t_в).

Общее число уравнений должно равняться числу неизвестных. 

6.На этом заканчивается этап постановки задачи. Мы получили систему уравнений, может быть, систему уравнений и неравенств, которые являются математической моделью решаемой нами задачи. В последний момент мы смотрим, а что, собственно, нам надо найти в этой задаче, и из состояния «физик» мы переходим в состояние «математик» и решаем эту систему в общем (буквенном) виде. Решать в общем виде – это строго обязательно. Всякая подстановка численных значений до получения общего ответа – это серьезное нарушение. Оценка за это снижается немилосердно! 

7.После того, как получен ответ в общем виде, мы снова переходим в состояние «физик» и занимаемся анализом задачи. Полезно посмотреть, к каким последствиям приводит увеличение или уменьшение величин, заданных в условии задачи. Посмотрите области допустимых значений. Проследите, чтобы размерности правой и левой части уравнений были одинаковы. Если у Вас метры складываются с секундами, идите в начало задачи и ищите ошибку. Замечательно, что Вы ошиблись, поиск своих или чужих ошибок – самый эффективный способ обучения. Когда все получается с первого раза – чему тогда учиться? 

8.Подставьте в буквенный ответ числовые значения заданных физических величин с наименованием их единиц. Предварительно надо выразить все числовые значения в одной системе единиц. Выполните вычисления и получите ответ. Пользуйтесь правилами приближенных вычислений. Следите, чтобы точность полученного ответа не превосходила точности заданных величин. К сожалению, составители задач редко правильно задают точность исходных величин. 

Перечисленные рекомендации не надо считать абсолютно жесткими, неизменными. Всего не предусмотришь. В некоторых случаях отдельные пункты можно опустить, иногда приходится вводить новые. Многие задачи проще решать графически. Но на первых этапах мы должны придерживаться этой схемы. Если где-то мы отходим от нее, то делать это надо осознанно. Когда Вы станете большими мастерами в решении задач по физике, тогда Вы можете импровизировать. А эталон, к чему надо стремиться, сформулировал Р.Фейнман 

Физик, это тот, кто видит решение задачи, еще не решая ее.

Приступаем к решению задач. Понятно, что первые задачи будут несложными. Надо привыкнуть к последовательному выполнению этапов решения задач по кинематике. 

Задача 1

Тело движется равномерно вдоль оси Х. Со скоростью v = 2 м/с противоположно положительному направлению оси Х. Найдите положение тела в момент времени t₁ = 10 с после начала движения, если начальная координата x₀ = 5 м. Чему равен путь, пройденный телом? 

Решение.

Выписываем в левом верхнем углу «Дано» и делаем рисунок. Иногда это полезно делать одновременно. 

Из условия задачи видно, что физической моделью задачи является материальная точка, двигающаяся по прямой с постоянной скоростью. Математической моделью такого процесса является математическое уравнение для координат материальной точки:

x = x₀+ v_xt.

По условию задачи v_x= -v и формула для координаты принимает вид:

x = x₀ - vt.

Пройденный телом путь равен

s = vt.

В этих уравнениях t – параметр, переменная величина. Уравнения показывают, как изменяется координата материальной точки и пройденный ею путь со временем t. Можно для большей ясности писать x(t) и s(t). Смотрим в условие задачи, что нам нужно найти. Координату и пройденный путь в момент времени t₁. Физика закончилась. Переходим в состояние «математик» и смотрим, что нам предстоит решить. В этой задаче работы для математика нет. Надо подставить вместо t ее численное значение t₁ и подсчитать численный ответ. Обратите внимание, t - переменная величена, а t₁ – число. В школьных задачах по физике, как правило, не бывает сложной математики. Поэтому когда Вы оформляете решение задачи в чистовике, математическую часть можно излагать предельно кратко. Леша Щекин на контрольных и олимпиадах выписывал исходную систему уравнений, потом сразу выписывал ответ в общем виде и численный ответ. Это правильно. Но когда Саша Головко записывал «Дано», потом замирал на какое-то время, а потом сразу писал ответ, то это уже слишком. Так поступать не следует. Экзаменатор может подумать, что Вы списали. 

Итак, мы имеем:

x(t₁) = x₀ – vt₁ = 5 м – 2 м/с·10 с = -15 м.

Пройденный телом путь равен

s(t₁) = vt₁ = 2 м/с·10 с = 20 м.

Анализ решения. 

Из уравнение для координаты видно, что тело из +? движется к началу координат, в момент времени t = 0 оно проходит координатуx₀ = 5 м, в момент времени 2,5 с оно проходит через начало координат и уходит в -?. С размерностями величин все в порядке. Поэтому у нас есть основания надеяться, что мы правильно решили задачу. 

Задача 2

Из пунктов А и В, расстояние между которыми l = 55 км, одновременно начали двигаться с постоянными скоростями навстречу друг другу по прямому шоссе два автомобиля. Скорость первого автомобиля v₁ = 50 км/ч, а второго v₂ = 60 км/ч. Через сколько времени после начала движения автомобили встретятся? Найдите пути, пройденные каждым автомобилем за это время. 

Решение.

Представим движение автомобилей как движение материальных точек. 

Примем пункт А за начало координат и направим координатную ось Х в сторону пункта В (см.рис.). Движение автомобилей будет описываться уравнениями:

x₁(t) = x₀₁ + v_1xt,

x₂(t) = x₀₂ + v_2xt.

Начальные условия:

x₀₁ = 0,x₀₂ = l.

Так как вектор скорости первого автомобиля направлен в положительном направлении, а второго – в отрицательном, то

v_1x = v₁,v_2x = -v₂.

Поэтому первые два уравнения перепишем в виде:

x₁(t) = v₁t,

x₂(t) = l – v₂t.

Когда в момент времени t₁ автомобили встретятся, они будут иметь равные координаты:

x₁(t₁) = x₂(t₁), 

или

v₁t₁ = l – v₂t₁.

Откуда

t₁ =l/(v₁ + v₂) = 0,5 ч.

Пройденные пути равны

s₁ =v₁t₁ = 25 км,s₂ = v₂t₁ = 30 км.

Анализ задачи. 

Задача слишком простая, чтобы что-то еще анализировать. Можно сложить s₁ + s₂, получается 55 км, значит, решили правильно, скорее всего. 

Задача 3

Движение точки на плоскости описывается уравнениями

х = 6 м + 3 м/с ·t,

y = 4 м/с ·t.

Определить траекторию движения точки и построить ее на плоскости XOY. 

Решение.

Исключим из обоих уравнений параметр t. Для этого выразим время из первого уравнения и подставим во второе, получим:

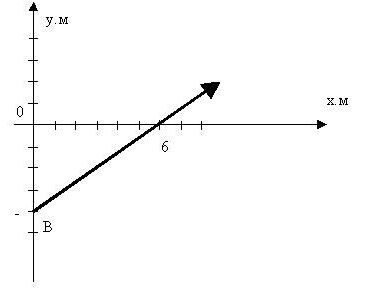
y = 4x/3 – 8 м.

Это уравнение прямой линии с угловым коэффициентом 4/3 и пересекающая ось OY в точке –8. Можно построить ее по точкам, 

при х = 0y = -8 ми при y = 0х = 6 м. 

Направление скорости движения точки укажем стрелкой. 

Задача 4

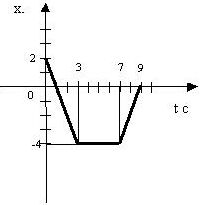
На рисунке изображен график зависимости от времени координаты точки, движущейся вдоль оси Х. Как двигалась точка? Постройте графики модуля v и проекции v_xскорости, а также пути в зависимости от времени. 

Решение.

В течение первых 3 с координаты точки изменялись от 2 м до – 4 м, следовательно, точка двигалась противоположно положительному направлению оси Х. Проекция скорости равна

V_1x = (- 4 – 2 )/ 3 м/c = - 2 м/c,

А модуль скорости равен v₁ = 2 м/с. 

Следующие 4 с точка не двигалась, ее координаты не изменялись, v_2x = v₂ = 0. Потом в течение 2 с точка двигалась в положительном направлении оси Х о пришла в начало координат (х = 0).Проекция и модуль скорости соответственно равны

v_3x = v₃ = (0 – (-4))/2 м/с = 2 м/с.

На рисунке «а» изображен график проекции скорости, на рисунке «б» – график модуля скорости, на рисунке «в» - график пути. При построении графика пути не забывайте, что путь не может быть отрицательным и при движении не убывает. 

Задача 5

С подводной лодки, погружающейся равномерно, испускаются звуковые импульсы длительностью t₁ = 30,1 с. Длительность импульса, принятого на лодке после его отражения от дна, равна t₂ = 29,9 с. Определите скорость погружения лодки v. Скорость звука в воде с = 1500 м/с. 

Решение.

Звуковой импульс не является материальной частицей, однако уравнения движения звукового импульса такие же, как и у материальной точки, поэтому можно применять законы кинематики материальной точки. 

За время t₁ лодка переместится на расстояние vt₁, поэтому расстояние в воде между началом импульса и его концом равно

L = ct₁ – vt₁.

Такая длина сигнала сохранится и после отражения от дна. Прием импульса закончится в тот момент, когда лодка встретится с задним концом импульса. Поскольку скорость их сближения равна с + v, то продолжительность приема равна

t₂ = L/(c + v)

Решая эти уравнения совместно, получим

v = = 5 м/с.

Список литературы.

https://easyfizika.ru/zadachi/kinematika/

https://phys-ege.sdamgia.ru/test?theme=204

Скачано с www.znanio.ru