Касательная к окружности_Приложение 1

Работа в группах

Теорема. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

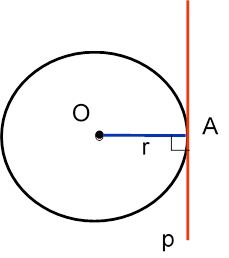
Дано: Окр.(О;r), р – касательная,  А – точка касания. Доказать: р     ОА. 

Доказательство:

А – точка касания, О – центр окружности, значит, ОА – радиус. Пусть касательная р не перпендикулярна ОА, тогда радиус ОА является наклонной к прямой р. Тогда перпендикуляр, проведённый из точки О к прямой р,

меньше наклонной ОА, т. е. расстояние от центра окружности меньше радиуса.

Значит, прямая р и окружность будут иметь две общих точки, но это

противоречит условию: р – касательная, т. е. она имеет с окружностью одну

общую точку. Следовательно, предположение, что р не перпендикулярна ОА неверно.

Значит, р     ОА. 

Теорема. Отрезки касательных, проведенных из одной точки, равны и углы между касательными и прямой проходящей через эту точку и  центр равны.

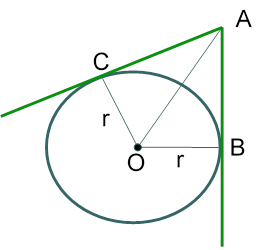Дано: Окруж.(О; r), АВ и  АС – касательные.

Доказать : АВ = АС,     ОАВ =     ОАС.

Треугольники OBA и OCA — прямоугольные, так как касательные перпендикулярны к радиусам в точках B и C. Сторона OA — общая. Катеты OB и OC равны как радиусы одной и той же окружности. Треугольники равны по гипотенузе и катету, отсюда равны и катеты AB и AC и углы BAO и CAO, то есть делит угол по пополам.