
Тема: "Угол между прямыми"
Цели урока:
Обучающие: организовать деятельность, направленную на формирование понятия угла между скрещивающимися прямыми и закрепление полученных знаний при решении задач.
Развивающие: способствовать развитию пространственного воображения учащихся, умений обосновывать или опровергать выдвигаемые предположения при решении геометрических задач, создать условия для формирования ключевых компетенций учащихся.
Воспитательные: средствами урока воспитывать у учащихся ответственное отношение к учебному труду, волевые качества личности, умение работать в коллективе.
Тип урока: Изучение нового материала.
План урока:
1.Организационный момент.
2. Актуализация знаний.
3. Целеполагание.
4. Изучение нового материала.
5. Физкультминутка.
6. Первичная проверка понимания темы.
7. Закрепление.
8. Подведение итогов. Рефлексия.
9. Информация о домашнем задании.
План урока:
I. Организационный момент.
· Приветствие. Психолого-педагогическая настройка учащихся на предстоящую деятельность.
· Проверка домашнего задания. Ответы на возникшие вопросы.
· Мотивация изучения нового материала.
Эпиграфом к нашему уроку послужит народная мудрость:
Жизнь не спросит,
что ты учил,
Жизнь спросит, что ты знаешь.
II. Актуализация знаний.
Метод – мозговой штурм
(Вопросы выводятся на презентацию и открываются ответы)
- Какие темы мы прошли на предыдущих уроках?
- Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
- Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться?
б) быть скрещивающимися?
- Могут ли скрещивающиеся прямые a и b быть параллельными прямой с?
- Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 лежат на прямой b. Как будут расположены прямые АВ и А1В1?
- Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с - скрещиваются?
Поисковый метод
Работа с интерактивной доской:
1. Изобразите пары параллельных, пересекающихся и скрещивающихся прямых на готовых моделях многогранников.
2. Найдите пары параллельных, пересекающихся, скрещивающихся прямых на изображении города.
III. Целеполагание.
Метод – эвристическая беседа
Учащимся задаются наводящие вопросы по теме урока. Эти вопросы являются целеполаганием для учащихся.
- Каково взаимное расположение прямых в пространстве?
- Все ли аксиомы и теоремы планиметрии применимы в стереометрии?
- Какую тему мы еще не прошли?
Учащиеся сами формулируют тему урока: "Угол между прямыми"
- Какой из четырех углов, полученных при пересечении двух прямых, мы называем углом между пересекающимися прямыми?
- Чему равен угол между двумя параллельными прямыми?
-
Чему равен угол между двумя скрещивающимися прямыми?
Учащиеся формулируют цель и задачи урока.
(Учитель ещё раз проговаривает тему, конкретизирует цель и задачи урока.)
IV. Изучение нового материала.
Наглядно-иллюстративный метод, эвристическая беседа
Использование интерактивной доски.
Расположение прямых в пространстве и угол между ними.
1. Пересекающиеся прямые.
2. Параллельные прямые.
3. Скрещивающиеся прямые.
Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.
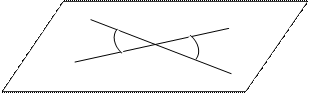 |
Углом между двумя
пересекающимися прямыми в пространстве называется наименьший из углов,
образованных лучами этих прямых с вершиной в точке их пересечения.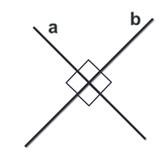
Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.
Угол между двумя параллельными прямыми равен 0°.
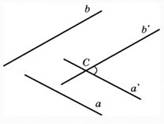
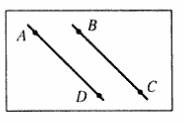
Проговорить метод параллельного переноса при нахождении угла между скрещивающимися прямыми.
Проблемный метод
Использование интерактивной доски.
Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a и b.
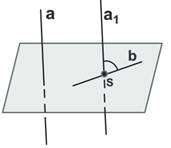 Угол
между скрещивающимися прямыми, как и между прямыми одной плоскости, не может
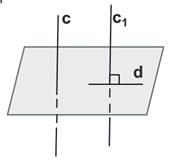
быть больше 90°. Две скрещивающиеся прямые, которые образуют угол в 90°,
называются перпендикулярными.
Угол
между скрещивающимися прямыми, как и между прямыми одной плоскости, не может
быть больше 90°. Две скрещивающиеся прямые, которые образуют угол в 90°,
называются перпендикулярными.
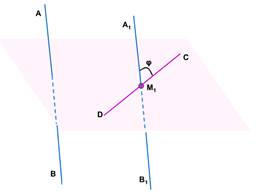
Пусть AB и CD – две скрещивающиеся прямые.
Возьмём произвольную точку М1 пространства и проведём через неё прямые А1В1 и C1D1, соответственно параллельные прямым AB и CD.
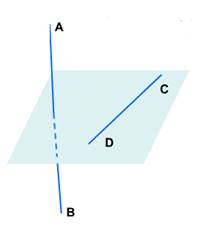
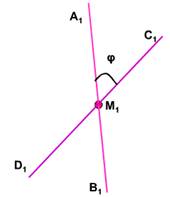
Если угол между прямыми А1В1 и C1D1равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ.
Постановка проблемы: Чтобы найти угол между скрещивающимися прямыми AB и CD в качестве точки M1 можно взять любую точку пространства?
Учащиеся выдвигают гипотезу: угол между скрещивающимися прямыми не зависит от выбора точки.
Исследовательский метод.
Учащиеся самостоятельно доказывают, зависит ли угол между скрещивающимися прямыми от выбора точки.
Делают вывод: угол между скрещивающимися прямыми не зависит от выбора точки.
V.Физкультминутка (демонстрация видеоролика)
VI. Первичная проверка понимания темы.
Приём «Найди ошибку».
Нужно найти ошибку на готовых чертежах на интерактивной доске и исправить её.
VII. Закрепление нового материала
Работа в парах с самопроверкой. Ответы выводятся по завершении работы. Работа по готовым чертежам.
Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.
![]()
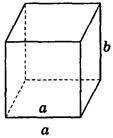 а)
90°;
а)
90°; 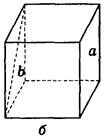 б) 45°;
б) 45°;
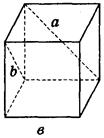 в) 60°;
в) 60°; 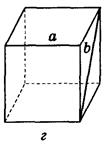 г) 90°;
г) 90°;
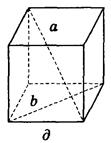 д) 90°;
д) 90°; 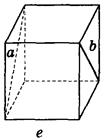 е) 90°.
е) 90°.
Решение задач: №1. Индивидуальная работа.
![]()
![]()
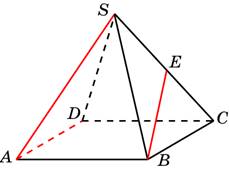 В правильной
пирамиде SABCD, все ребра
которой равны 1, точка E – середина ребра SC. Найдите угол
между прямыми AD и BE.
В правильной
пирамиде SABCD, все ребра
которой равны 1, точка E – середина ребра SC. Найдите угол
между прямыми AD и BE.
Решение:
Искомый угол равен углу CBE.Треугольник SBC– равносторонний.
ВE – биссектриса угла 60°. Угол CBE равен 30°.
Ответ:30°.
№267.
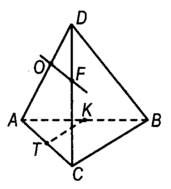 DABC – тетраэдр, точка
О и F – середины ребра AD и CD соответственно,
отрезок TK – средняя линия
треугольника ABC.
DABC – тетраэдр, точка
О и F – середины ребра AD и CD соответственно,
отрезок TK – средняя линия
треугольника ABC.
a) Чему равен угол между прямыми OF и CB?
b) Верно ли, что угол между прямыми OF
и TK равен 60°?
c) Чему равен угол между прямыми TF и DB?
Дано: DABC-пирамида, О – середина AD, F – середина CD,
ТК – средняя линия ∆АВС.
Решение:
a) В плоскости АВС
через точку С проходит прямая АС, параллельная прямой OF (т.к. OF – средняя линия
∆АВС, поэтому ![]() АСВ – угол между скрещивающимися
прямыми OF и СВ. ∆АВС
– правильный, поэтому
АСВ – угол между скрещивающимися
прямыми OF и СВ. ∆АВС
– правильный, поэтому ![]() АСВ=60°.
АСВ=60°.
Ответ: 60°
b) Т.к. OF || AC и TK || CB, то угол между прямымиOF и TK равен углу между прямыми AC и CB, т.е. 60°.
Ответ: верно.
c) Т.к. TF || AD (по свойству
средней линии), то ![]() ADB=60°.
ADB=60°.
Ответ: 60°
Решения выводятся на экран для проверки
VIII. Подведение итогов. Рефлексия.
· Что мы узнали нового?
· Справились ли мы с теми задачами, которые были заданы в начале урока?
· Какие задачи мы научились решать?
Выставление отметок за урок.
Вернёмся к цели урока и оценим итоги с помощью приема «Звезда сбывшихся ожиданий» с использованием интерактивной доски.

IX. Информация о домашнем задании.
§4 (стр. 85-89). Уметь объяснить понятие угла между скрещивающимися прямыми. Решить задачи №269, №275. Повторить теорему косинусов.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.