
ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ РАБОТЫ
ПО МЕТОДИКЕ ПРЕПОДАВАНИЯ МАТЕМАТИКИ
Под редакцией Е.И. Лященко
ДОПУЩЕНО ГОСУДАРСТВЕННЫМ КОМИТЕТОМ СССР по НАРОДНОМУ ОБРАЗОВАНИЮ В КАЧЕСТВЕ УЧЕБНОГО ПОСОБИЯ ДЛЯ СТУДЕНТОВ ФИЗИКО-МАТЕМАТИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ ПЕДАГОГИЧЕСКИХ ИНСТИТУТОВ
МОСКВА «ПРОСВЕЩЕНИЕ» 1988
ББК 74.262
Л 12
Авторы: Е. И. Лященко, К. В. Зобкова, Т. Ф. Кириченко, З. И. Новосельцева, Н. Л. Стефанова
Рецензенты: кафедра методики преподавания математики Киевского государственного педагогического института им. А. М. Горького (зав. Кафедрой кандидат педагогических наук, доцент З. И. Слепкань); кандидат педагогических наук, доцент В. А. Байдак; кандидат педагогических наук, доцент А. М. Янченко
Л 12 Лабораторные и практические работы по методике преподавания математики: Учеб. пособие для студентов физ.-мат. спец. пед. Ин-тов / Е. И. Лященко, К. В. Зобкова, Т. Ф. Кириченко и др.; Под ред. Е. И. Лященко. - М : Просвещение, 1988.-223 с.: ил.
ISBN 5-09-000600-8
В книге приведено содержание лабораторных и практических работ по методике преподавания математики, даны рекомендации по их выполнению. Пособие направлено на формирование у будущего учителя математики творческого подхода к организации учебно-воспитательного процесса.
Л 4309020000--766 20--88 103(03) -- 88
ББК 74.262
ISBN 5-09-000600-8
© Издательство «Просвещение», 1988
Предисловие
В настоящем пособии приведено содержание лабораторных и практических работ по методике преподавания математики в средней школе. В нем получили свое дальнейшее развитие и конкретизацию идеи, составляющие основу общей методики преподавания математики.
Очень важным для будущего учителя является не рассмотрение отдельных фактов предмета, а методическая и логическая концепция предмета в целом. Поэтому необходимо хорошо знать те методические умения, которыми должен обладать учитель математики, видеть конкретные методические модели изучения компонентов содержания учебного материала школьного предмета математики (понятий, теорем, математических задач как средства обучения и т.д.), уметь проводить логико-дидактический анализ учебного материала (как отдельных уроков, так и темы в целом), уметь выделять отдельные содержательные линии предмета. В связи с этим будущие учителя математики должны четко представлять себе основные виды деятельности, которые придется им выполнять в своей практической работе. С этого начинается книга.
Далее приводятся лабораторные работы, которые объединены в параграфы в соответствии с группами методических умений. К каждой лабораторной работе указаны ее тема, цели, средства обучения, основное содержание, задания для самостоятельной работы, отдельные образцы оформления результатов самостоятельной работы, литература.
В третьей главе раскрыты общие подходы к выполнению логико-дидактического анализа школьного курса математики и на примере нескольких тем: «Многоугольники», «Неравенства», «Интеграл», «Тригонометрические функции» раскрыта методика анализа этих тем, дан пример составления развернутых тематических планов и конструирование методики их изучения в школе, поставлены методические задачи, предложен методический анализ одной из математических линий школьного курса математики - линии уравнений.
Настоящее пособие согласовано с циклом лекций по курсу «Методика преподавания математики» и «Практикумом по решению задач», что нашло отражение в приведенной в пособии объединенной рабочей программе.
Работа авторов над содержанием пособия распределяется следующим образом : глава I, в главе II § 4, в § 5 лабораторные работы № 1, 12, 13, 14, 16, в главе III § 8 и 8.1 - Е. И. Лященко; в главе II лабораторные работы № 5, 6, 10, 19 и в главе III § 8.2 и § 11 — К. В. Зобкова; в главе II лабораторная работа № 7, § 7 введение и № 18, в главе III § 9 — Т. Ф. Кириченко; в главе II лабораторные работы № 2, 11, 17 — З. И. Новосельцева; в главе II лабораторные работы № 3, 4, 8, 9, 18, в главе III § 10 — Н. Л. Стефанова.
Авторы выражают благодарность рецензентам пособия : кандидату педагогических наук, доценту В. А. Байдаку, кандидату педагогических наук, доценту А. М. Янченко, кафедре методики преподавания математики Киевского государственного педагогического института им. А. М. Горького (заведующая кафедрой — кандидат педагогических наук, доцент З. И. Слепкань).
Замечания и предложения по улучшению пособия просим присылать по адресу: 129846, Москва, 3-й проезд Марьиной рощи, д. 41, издательство «Просвещение», редакция математики.
Глава I
ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ МАТЕМАТИКИ И ПРАКТИЧЕСКАЯ СИСТЕМА ЕЕ ОРГАНИЗАЦИИ
§ 1. ОСНОВНЫЕ ПРОФЕССИОНАЛЬНЫЕ УМЕНИIЯ УЧИТЕЛЯ МАТЕМАТИКИ
Основные виды деятельности учителя. Учителю математики в своей практической работе приходится выполнять различные виды деятельности. Педагогическую деятельность учителя будем понимать как совокупность отдельных деятельностей, в которую включаем следующие: анализировать различную литературу, включая программы, учебники, учебно-методические комплекты и другие средства обучения, и на этой основе с учетом возрастных возможностей учащихся отбирать необходимый материал и из него конструировать предметное содержание урока или любого другого вида занятий с учащимися; планировать свою работу и учить планировать учебную работу учеников; организовывать различные виды деятельности учащихся, помогать их выполнять и в определенной мере управлять ими; оценивать свою деятельность и деятельность учащихся, учить их оценке и самооценке.
Названные виды деятельности, конечно, не охватывают все виды деятельности, которые могут встретиться учителю в его практической работе. Но, во-первых, все виды деятельности и нельзя предусмотреть, так как практика многообразнее любой систематики. Во-вторых, каким-то видам деятельности как основным в начале приобретения профессии человек должен научиться, сформировав при· этом основные умения и самооценку, а затем заниматься продолжением и совершенствованием своего образования и профессионального мастерства.
Ориентир на основные виды деятельности учителя математики является определяющим при формировании его профессиональных умений. Вторым фактором, существенно влияющим на первичный уровень сформированности профессиональных умений, будет выделение основной единицы организации учебного процесса - урока. В основном на уроке учитель формирует все стороны учебной деятельности ученика; поэтому и его, учителя, деятельность должна фокусироваться вокруг урока.
Одним из основных видов деятельности учителя является аналитико-синтетическая деятельность, состоящая в осознании и принятии широких И узких целей обучения, воспитания и развития учащихся. Этот вид деятельности включает в себя: логико-математический анализ учебного материала школьных учебников и задачников по математике; логико-дидактический анализ учебного материала школьных учебников; методический анализ математической литературы и литературы по педагогике, психологии, истории математики, методике преподавания других школьных предметов и др.; методический анализ различных средств обучения ― наглядности, технических средств обучения, обучающих возможностей ЭВМ и др. Аналитическую деятельность учитель должен осуществлять с условием, что весь учебный материал и все средства анализируются с одной целью: научить ученика самостоятельно разбираться в учебном материале. Значит, в основе анализа любого материала, кроме логической и содержательной его части, должны быть учтены цели изучения этого материала, а последние непосредственно связаны с интеллектуальными, эмоциональными и волевыми возможностями учащегося. Результат анализа возможностей отдельных учащихся и коллектива учащихся в целом, концепций обучения и специфики учебного материала позволит учителю правильно отобрать учебный материал, на основе которого осуществляется обучение.
Важный вид деятельности учителя ― планирование и конструирование. Этот вид деятельности включает в себя тематическое и календарное планирование учебного материала, планирование уроков (разработка подробных конспектов уроков и развернутых планов уроков, занятий кружка или факультатива и др.). На основе выполненного анализа учебного материала и средств обучения с учетом четко сформулированных целей обучения и поставленных учебных задач учитель конструирует урок, основные моменты которого найдут отражение в конспекте или развернутом плане урока или другого учебного дела.
Учитель должен уметь выполнять еще один вид деятельности ― организовывать деятельность учащихся на различных видах занятий и управлять этой деятельностью на разных ее этапах. Этот вид деятельности включает в себя организацию учащихся на сознательное отношение к разным видам деятельности на уроке: к слушанию учителя и товарища, к чтению учебников и научно-популярной литературы, к решению разнообразных математических задач, к самостоятельной работе с различным учебным материалом на уроке и дома, к подготовке рефератов, к решению нестандартных математических задач, к подготовке докладов и др. Управление деятельностью учащихся может осуществляться различными путями: 1) косвенное управление ― через соответствующий набор учебного материала и средств обучения; 2) прямое управление ― через формирование определенных учебно-познавательных действий и действий контроля и самоконтроля.
И еще один вид деятельности учителя ― деятельность по организации различных форм контроля работы учащихся (устный опрос учащихся ― фронтальный и индивидуальный, письменные работы ―с комментарием отдельных этапов у доски, обучающие самостоятельные работы, контрольные работы) и правильной оценки этой работы. Студент ―будущий учитель должен непрерывно учиться этому виду деятельности. Точная постановка вопроса, комментирование ответов товарищей, рецензирование их работ, составление планов ответов, анализ ответов в соответствии с составленным планом и т.д. - все это формирует умение правильной оценки деятельности других людей. Формирование самооценки осуществляется путем анализа ошибок в своей работе на основе образца решения, предписания или контр примеров и др.
Учебные и методические умения учителя. В советской педагогике и психологии существуют различные трактовки понятия «умение»: а) умение как освоенное действие; б) умение как способность использовать имеющиеся знания; в) умение как совокупность навыков; г) умение как не вполне завершенный навык или один из существенных этапов в выработке навыка и др.
Наиболее современным и перспективным рассмотрение этого понятия представляется в концепции учебной деятельности. Структура учебной деятельности включает в себя следующие компоненты: учебно-познавательные потребности и мотивы; учебно-познавательная задача; действия и операции, с помощью которых будет решена учебно-познавательная задача; рефлексия и анализ и на их основе действия оценки и самооценки осуществленной учебно-познавательной деятельности.
Так как педагогическую деятельность рассматривают как совокупность деятельностей. а многие из этих деятельностей имеют в своей основе учебно-познавательную деятельность, то в трактовке понятия «умение» будем исходить из структуры учебной деятельности. Учебная деятельность реализуется с помощью определенных учебно-познавательных действий. Например, при усвоении знании осуществляется анализ происхождения знаний, раскрывается их структура, происходит моделирование знаний на более удобном языке, осуществляется их обобщение и конкретизация и т.п. Поэтому вполне правомерно понимать умение как освоенное действие. При этом уровень освоения действия может быть разным. Учебно-познавательные действия - это объективный факт. Он может быть определен заданием, указанием, рекомендацией, вопросом. Умение ― это субъективный факт, т.е. характеристика овладения действием конкретного человека. Действия в значительной мере соотносятся с учебным материалом, умения ― с человеком.
Однако беспредметное понимание умений как освоенных действий еще не дает полного раскрытия структуры этого понятия. Действия раскрываются через операции, а последние имеют разную природу. Бывают механические операции: операции по забиванию гвоздя, операции при вышивании и др. Бывают интеллектуальные: операции при выборе знаний для доказательства теорем, операции при планировании учебного материала, операции для обоснования существования какого-нибудь объекта и т. п. Учебно-познавательные действия в своей основе интеллектуальные, и в этом их существенная особенность. Вторая существенная особенность учебно-познавательных действий ―их двоякая основа. С одной стороны, есть действия, идущие непосредственно от изучаемого предмета. Например, действия разложения квадратного трехчлена на множители, построение треугольника, подобного данному, приведение подобных слагаемых и т.п. Такие действия часто называют специфическими или предметными. С другой стороны, есть действия общеучебные и общепознавательные, которые не связаны непосредственно с изучением того или иного учебного предмета, однако они должны формироваться в определенной мере и использоваться при обучении конкретным учебным предметам. К таким действиям относятся: анализ и синтез, сравнение и классификация, доказательство и подведение под понятие и др. Чтобы формировать учебные действия, как отмечает В. В. Давыдов ([59] *, с. 164), необходимо учебным действиям придавать конкретную форму, соответствующую тому или иному учебному предмету, и, кроме того, учебные умения формируются у школьников на основе выполнения действий в «процессе длительного усвоения конкретных «предметных знаний» ([59], с. 164).
* Здесь и далее число в скобках [ ] означает ссылку на соответствующий источник из списка литературы, помещенного в конце книги.
Таким образом, учебные умения при изучении предмета математики, как и любого другого учебного предмета, формируются у учащихся на основе синтеза предметных и общеучебно-познавательных действий в процессе длительного усвоения математических знаний.
Уровни сформированности умений могут быть разные. Для учебно-познавательных умений обычно выделяют три уровня сформированности: 1) уровень воспроизведения; 2) уровень применения умений в аналогичной ситуации; 3) уровень творческого использования умений в новой нестандартной ситуации.
Учебная деятельность будет сформирована тогда, когда учащийся сможет заниматься самообразованием. А это значит, что он должен уметь выполнять действия целеполагания и мотивации, действия постановки учебных задач, действия отбора содержательных средств и учебных действий для решения учебных задач, действия оценки и самооценки.
Итак, учебные умения ― это действия по реализации учебной деятельности, причем эти действия есть синтез общеучебно-познавательных и предметных действий.
Для выяснения содержания и необходимого набора методических умений учителя математики необходимо раскрыть сущность профессиональных действий учителя.
Учитель математики обычно в своей профессиональной деятельности отвечает на несколько вопросов: 1) Зачем надо учить математике? 2) Что надо изучать? 3) Как надо обучать математике? ([95J, с. 7.) Нам представляется целесообразным либо в вопросе «Как надо обучать математике?» всегда держать во внимании еще один вопрос «Как оценивать результаты обучения математике?», либо выделить его в самостоятельный в силу его архиважности в ситуации всеобщего обязательного среднего образования, так как ответ на этот вопрос должна дать методика обучения предмету .и у каждого предмета есть свои особенности. Только при правильной организации оценки деятельности учащихся оценка может и должна выступать как источник ее стимулирования.
Предметные действия , раскрывающие процесс подготовки к уроку и его проведения, будут следующие: действия целеполагания и мотивации; действия логико-дидактического анализа учебного материала; действия постановки учебных задач; действия отбора средств и методов обучения в соответствии с поставленной учебной задачей и наличием средств обучения; действия по организации и управлению процессом учения и обучения; действия по формированию оценки и самооценки.
Нетрудно видеть, что ряд действий, посредством которых реализуется учебная деятельность, и предметные действия по методике преподавания математики имеют одинаковое название. Так, например, действия целеполагания и мотивации есть и в учебной деятельности учащихся, и в деятельности учителя (методическая деятельность или профессиональная деятельность). Различие их прежде всего — в направленности на объект, а затем — и в уровне сформированности и обобщенности. Учащийся сам ставит цель (это высший уровень целеполагания): изучить какое-то предметное содержание, решить математическую задачу, овладеть определенным математическим методом или алгоритмом. В этом случае цель направлена на себя, т.е. я (учащийся) осознаю, что необходимо изучить что-то или решить какую-то математическую задачу. Потребность, мотивы и цель способствуют четкому определению перспективы деятельности, и цель в этом случае направлена на субъект учения (учащегося).
Учитель в действии целеполагания предполагает иную направленность. Его действия направлены на объект обучения ― учащегося. Поставленную им цель еще надо учащемуся принять. Значит, нужна .деятельность по принятию цели. Необходимо ученику показать действия и приемы принятия цели и ее постановки. А для этого учитель сам должен владеть приемами постановки и принятия цели как в зависимости от содержания учебного материала, так и от ситуации, в которых возможно будет решать вопросы обучения и воспитания учащихся. И кроме того, умение целеполагания у учащихся, как отмечают психологи, может быть сформировано только к последним годам обучения; поэтому к профессиональным умениям учителя в связи с формированием действия целеполагания необходимо отнести и умения по принятию цели. В связи с этим одним из существенных направлений профессиональной деятельности учителя есть формирование действия целеполагания в широком его смысле, т. е. в процессе изучения предмета предполагать и формирование определенных черт личности, жизненных позиций, мировоззренческих установок и т. п.
В учительской (профессиональной) деятельности есть и свои специфические (предметные) действия, не совпадающие с учебными действиями. Это такие действия, как логико-математический и логико-дидактический анализ учебного материала, действия по отбору средств и методов обучения, действия контроля и оценки и др.
К числу методических умений следует отнести и такие общие учебно-познавательные действия, как анализ и синтез, обобщение и конкретизация, сравнение и классификация и др.
Содержание деятельности учителя математики опирается на определенные профессиональные знания: знание о различных аспектах вопроса постановки целей обучения математике (цели изучения тем, разделов, методов, решения задач, доказательства математических утверждений и др.); знание о прием ах принятия целей изучения учебного материала; знание о специфике учебных, математических и методических задач и прием ах их формулировки и постановки; знание о действиях и соответствующих им операциях для решения определенных классов математических, учебных и методических задач; знание о средствах обучения, способах их реализации при обучении различным вопросам в соответствии с целями и методами обучения; знание о приемах организации деятельности учащихся и управления этой деятельностью; знание о различных формах контроля и приемах оценки деятельности учащихся и формирования самооценки у учащихся.
Мы перечислили основные профессиональные теоретические знания. Ранее были названы основные действия профессионального характера. Для того чтобы эти действия перешли в умения профессионального характера, необходимо длительное время решать учебные и методические задачи. В процессе их решения приобретаются методические умения.
В методических умениях, как и в учебных, необходимо различать также несколько уровней их сформированности.
Первый уровень сформированности методических умений сводится к осознанию цели выполнения того или иного методического или учебно-познавательного действия, осмыслению его операционного состава, поиску способов выполнения чаще всего на основе образца, предложенного в инструкции.
Второй уровень — перенос отдельных сформированных методических умений, а иногда и целых комплексов на новые предметные объекты и более крупные блоки учебного материала (на математический метод, тему, тип математических задач и т.п.). Перенос этот чаще всего осуществляется на основе осознания цели и путем использования общих рекомендаций и общих эвристик.
Третий уровень — высокоразвитое методическое умение, которое определяется осознанием не только цели, но и мотивов и средств выбора способов деятельности. Этому уровню характерно использование различных средств и методических умений в соответствии с конкретной педагогической ситуацией.
В соответствии с уровнями формирования методических умений, их предметной сложностью и спецификой применения на педагогической практике эти умения можно разделить на несколько групп. Приводим одну из возможных группировок методических умений.
Первая группа методических умений в значительной мере связана с первым уровнем их формирования:
1. Умение выполнять логико-математический анализ определений математических понятий, математических утверждений, правил, алгоритмов, сюжетных математических задач.
2. Умение выполнять логико-дидактический анализ конкретного, самого минимального, содержательно законченного раздела учебного материала учебника, чаще всего пункта.
3. Умение организовывать поиск решения математической задачи, доказательства математического утверждения.
4. Умение подбирать задачи для обучения понятиям, доказательству математических утверждений, формированию правила или построению алгоритма.
5. Умение изготовлять простейшее учебное или наглядное пособие, материал для кодоскопа и др.
6. Умение работать со справочником, таблицей и другими аналогичными материалами и обучать этой работе учащихся.
7. Умение подбирать литературу для изучения конкретного вопроса (теоремы, задачи, пункта учебника) и составлять соответствующую картотеку.
8. Умение составлять систему вопросов для фронтальной проверки усвоения определенного конкретного знания (понятия, теоремы, правила и т. п.), составлять самостоятельную работу для проверки определенных математических или учебных умений учащихся, составлять контрольную работу для проверки конкретных знаний и умений учащихся.
9. Умение оценивать письменную обучающую или контрольную работу и анализировать ее результаты.
10. Умение располагать материал на доске, оформлять решение сюжетной задачи, доказательство математического утверждения, нахождение значения числового выражения или выражения с переменной и др.
Вторая группа методических умений предполагает второй уровень их формирования с учетом педагогической специфики изучения учебного материала:
1. Умение определять цели изучения конкретного учебного материала (определения понятия, теоремы и др.).
2. Умение на основе поставленной цели изучения учебного материала выполнять его логико-дидактический анализ (выделять ядерный материал, ведущие идеи темы, типизировать математические задачи и др.).
3. Умение мотивировать изучение конкретного учебного материала (темы, математической задачи, теоремы и др.).
4. Умение четко ставить учебную задачу и отбирать соответствующие ей учебные действия и операции.
5. Умение организовывать деятельность учащихся и управлять ею в процессе решения учебной задачи (приемы постановки вопросов, подбор средств для решения учебной задачи, постановка организующих и управляющих вопросов и вариантов одного и того же вопроса, приемы реакции на ответ и др.).
6. Умение составлять календарный план темы на основе ее логико-дидактического анализа.
7. Умение подбирать материал к уроку и писать конспект или развернутый план урока.
8. Умение анализировать урок с учетом целей его проведения и учебного материала.
9. Умение анализировать ответ учащегося, давать ему оценку.
10. Умение реферировать и рецензировать статьи (пособия) дидактического, педагогического и психологического содержания.
11. Умение составлять картотеку к докладу, для изучения конкретной темы.
Третья группа методических умений синтезирует все ранее сформированные умения и реализуется на любом учебном материале:
1. Умение выполнять логика-дидактический анализ школьного учебника, а также анализ реализации в учебниках определенной математической идеи, линии.
2. Умение определять иерархию целей обучения конкретной теме, курсу, предмету и конструировать систему ее реализации.
3. Умение создавать вариативную методику обучения в зависимости от целей и реальных условий обучения.
Для формирования названных умений необходима система теоретической и практической подготовки. Она обеспечивается через цикл методических предметов. С целью осмысления всей системы методической подготовки, места и функции каждого из предметов приводим возможный вариант рабочей программы по предметам методического цикла (табл. 1).
§ 2. ЦЕЛИ И СИСТЕМА ПРОВЕДЕНИЯ ЛАБОРАТОРНЫХ И ПРАКТИЧЕСКИХ РАБОТ ПРИ ФОРМИРОВАНИИ ПРОФЕССИОНАЛЬНЫХ УМЕНИЙ УЧИТЕЛЯ МАТЕМАТИКИ
Лабораторные работы и практические занятия по методике преподавания математики в главной своей части направлены на достижение следующих целей:
1. Выработка некоторых методических умений, которые в значительной мере возможно сформировать на занятиях. Эти умения не связаны непосредственно с проведением уроков и внеклассных дел.
Среди них — умение ставить вариативные цели изучения вопроса, темы, решения задачи, проведения урока и т.п.; подбирать учебный материал и средства обучения для достижения цели и разрабатывать методику реализации поставленной цели.
2. Умение проводить анализ уроков математики учителей.
3. Подготовка полных конспектов и развернутых планов урока и проведение некоторых из них или их фрагментов в форме «деловой» игры на занятиях.
Чтобы поставленные цели были достигнуты и в процессе выполнения лабораторных и практических работ были сформированы профессиональные умения, необходима самооценка предшествующей подготовки.
В основу самооценки могут быть положены ответы на различные вопросы, но они обязательно должны в какой-то мере фиксировать общий уровень подготовки по математике, педагогике и психологии.
Приведем некоторые вопросы, ответы на которые будут служить основой для самооценки готовности к изучению курса методики преподавания математики:
1. Что изучает математика?
2. Приведите пример определения любого математического понятия. Проанализируйте структуру приведенного вами определения понятия. Какие виды определений вы знаете? Приведите примеры.
3. Для математики не имеет значения (решающего) предмет. исследуемый ее средствами, а более важен применяемый метод. Какие вы знаете методы вузовских предметов: алгебры, геометрии и математического анализа? Что из них и в какой форме можно перенести в школьный предмет математики? Приведите примеры.
4. Как вы понимаете прикладную направленность математики? Что такое моделирование в математике? Приведите примеры.
5. Что является предметом изучения алгебры (геометрии, математического анализа) в вузе и как этот предмет представлен в школьном курсе математики? Покажите связи между этими предметами на конкретных примерах.
6. Что вы отнесете к понятию «аппарат алгебры» («аппарат математического анализа»)? Как и в каком виде он используется в школьном курсе математики? Приведите примеры.
7. Что такое теорема? логическая структура теорем, виды теорем? связь между прямым и обратным, противоположным и противоположным обратному утверждениями? На конкретном примере одного утверждения покажите связь между всеми четырьмя видами утверждений.
8. Что значит доказать математическое утверждение? Какие элементы в содержании понятия «доказательство» вы можете выделить? Покажите на каком-нибудь конкретном примере структуру математического доказательства.
9. Какими существенными свойствами обладает алгоритм? Установите общность и различие между понятиями «алгоритм», «правило», «формула».
Таблица 1
Рабочая объединенная программа по предметам методического цикла
|
Курс |
Лекция |
Лабораторные и практические работы |
Практикум по решению математических задач |
Педагогическая практика |
|
I
II
III
IV |
Курс «Введение в специальность» (6 ч): 1. Процесс обучения математике 2. Организация и проведение внеклассной работы по математике 3. Система НИРС на математическом факультете
1. Общая методика обучения математике (14-16 ч): - предмет методики преподавания математики (МПМ); - анализ программ и учебников; - формирование математических понятий; - обучение математическим утверждениям; - математические задачи; - основные методы обучения математике 2. Методика обучения числовым множествам(8-10 ч) 3. Методика обучения тождественным преобразованиям алгебраических выражений (2-4 ч) 4. Методика обучения функциям в восьмилетней школе (4 ч) 5. Методика обучения уравнениям в восьмилетней школе (4 ч) 6. Логическая структура курса планиметрии и особенности его изучения (4 ч) 7. Методика обучения равенству фигур (4 ч) 8. Векторы и подобие в школьном курсе геометрии (6 ч)
1. Методические особенности обучения стереометрии в школе на материале темы «Параллельность в пространстве» (4 ч) 2. Методика обучения тригонометрическим функциям в школе (4 ч) 3. Методические особенности обучения началам математического анализа в школе (4 ч) 4. Методика обучения показательной, логарифмической и степенной функциям (4 ч) |
1. Работа с математическими терминами и символами (2 ч) 2. Методика использования исторического материала по математике (2 ч) 3. Деловая игра «Формы проведения внеклассной работы по математике» (2 ч)
1. Общие вопросы (8-1O ч): -планирование работы учителя математики; - наглядность; - формы и методы проверки знаний; - конспект урока 2. Логико-математический анализ содержания и решения учебных и методических задач (12-14 ч); - теорем; - алгоритмов; - математических задач 3. Посещение уроков в школе (6-8 ч): - математики в V-VI классах; - алгебры в VII-VIII классах; - геометрии в VII-VIII классах; 4. Математические методы в школьном курсе математики: - аксиоматический (4 ч); - координатный (4 ч); - векторный (2 ч); - геометрических преобразований (2 ч); - уравнений и неравенств (2 ч); - производной и интеграла (2 ч); - параллельного проектирования (IV курс) (2 ч)
Логико-дидактический анализ тем школьного курса математических задач: - многоугольники (8 ч); - перпендикулярность в пространстве (4 ч); - многогранники (4 ч); - тригонометрические функции (6 ч); - применение производной (4 ч); - применение интеграла (4 ч); - показательная и логарифмическая функции (4 ч); - измерение длин, площадей и объемов (6 ч); - посещение уроков алгебры и геометрии в IX-XI классах (4 ч) |
1. Доказательство тождеств и неравенств: - способы доказательства тождеств и неравенств (6 ч); - классические неравенства (4 ч); - метод математической индукции (4 ч) 2. Решение рациональных и дробно-рациональных уравнений и неравенств,их систем. Способы и приемы решения: рациональных уравнений и неравенств (6 ч); - дробно-рациональных уравнений и неравенств (6 ч); - уравнений, содержащих модуль (4 ч) Обсуждение серии типовых задач, решаемых в школе (4 ч) 3. Метрические соотношения в плоских фигурах (6 ч) 4. Геометрические места точек (4 ч) 5. Геометрические преобразования (4 ч) 6. Решение задач на построение, доказательство. Вычисления (10 ч) 7. Решение сложных задач по всему школьному курсу планиметрии (8 ч) 1. Вопросы теории задач и методика работы над сюжетной задачей. Обсуждение подобранных студентами серий задач и методики работы с ними (10 ч) 2. Решение уравнений, неравенств и их систем, содержащих: - иррациональные выражения (6 ч); - показательные и логарифмические выражения (8 ч) Разбор разработок студенческих методических рекомендаций по мотивации решения задач, занятий математического кружка, серий типичных школьных задач, серий подготовительных задач для поиска решения основной задачи и др. (8 ч) 3. Четность и нечетность, периодичность функций (4 ч) 4. Обратные тригонометрические функции: - тождественные преобразования выражений (4 ч); - доказательство тождеств (6 ч) 5. Решение тригонометрических уравнений и неравенств: - основные типы тригонометрических уравнений и приемы их решения (4 ч); - типы тригонометрических уравнений, решаемых в школе, и поиск рационального их решения (4 ч); - решение тригонометрических неравенств, подбор задач для групповой работы в классе (4 ч) 1. Взаимное расположение прямых и плоскостей (8 ч) 2. Двугранные и многогранные углы (4 ч ) 3. Многогранники и сечение многогранников (8 ч); - разработка серии кодопозитивов для поиска решения задачи 4. Вычисление площадей поверхностей и объемов многогранников тел вращения(10 ч): - подбор серии вспомогательных задач ; - разработка методики поиска решения задач; 5. Комбинация многогранников и тел вращения (8 ч): - задачи на доказательство и вычисления; - подбор задач для школьной олимпиады 6. Геометрические задачи на вычисления с параметрами (8 ч): - допускаемые значения параметров исследования 7. Неравенства в задачах геометрического содержания (8 ч): - поиск решения; - подбор задач для кружковых занятий 8. Решение олимпиадных задач по курсу математики (10 ч) 9. Разработка методики поиска решения задач (6 ч) |
Школьный практикум (4 ч в неделю). Педагогические отряды: - занимаются отдельными внеклассными делами (викторины, математические газеты, вечера. игры и др.)
Школьный практикум (4 ч в неделю). Каждый студент: - проводит внеклассные занятия по математике; - принимает участие в оборудовании школьных математических кабинетов; - посещает уроки математики
Методическая педагогическая практика: - отдельные уроки с целью отработки конспекта урока (4-5 уроков); - цепь взаимосвязанных уроков (4-6 уроков); - контрольная работа и ее анализ (2-3 урока); - внеклассные дела по предмету; - помощник классного руководителя
Стажерская практика: - 3-4 урока для отработки умений по подготовке развернутого плана урока; - 15-16 уроков в одном классе без перерыва (алгебра и геометрия); - внеклассная работа по предмету; -работа классного руководителя |
Для актуализации знаний по педагогике и психологии можно предложить следующие вопросы:
1. Какие теории обучения вы знаете и каким из них отдаете предпочтение? Почему?
2. Как вы считаете: ученик — это объект или субъект обучения? Какова ваша точка зрения на этот вопрос? Дайте ей обоснование.
3. Любое педагогическое дело начинается с определения цели его проведения и конкретных педагогических задач. Что влияет на определение (постановку) цели и как конкретные педагогические задачи связаны с целью? Приведите примеры.
4. Какие средства обучения вы знаете? От чего зависит выбор конкретных средств обучения?
5. Какие приемы организации и управления деятельностью учащихся вы знаете? Приведите примеры использования отдельных приемов организации детей на выполнение конкретного дела. Какие приемы для этого использовали ваши школьные учителя? Какими приемами организации и управления деятельностью учащихся пользовались вы в своем педагогическом опыте, если он был?
6. Какие приемы оценки деятельности учащихся вам представляются более результативными? Дайте обоснование своему ответу.
7. В опыте вашей работы как студента или педагога (на педагогической практике) обязательно была работа с книгой (учебной конкретно). Какими приемами работы с книгой вы владеете? Какие приемы работы с книгой знаете, но пока не использовали?
8. Какие формы планирования работы учителя вы знаете?Как планируете свою работу в вузе? Как анализируете результаты выполнения своих планов, если таковые имеют место?
Выполнив самооценку и определив степень готовности к формированию нового качества и уровня профессиональных умений, считаем полезным ознакомиться с полной системой практических и лабораторных работ по методике преподавания математики. Эта система представляется в развитии и тем самым раскрывает последовательность деятельности, позволяющую четко определить основные этапы формирования профессиональных умений.
В первом цикле лабораторных работ (8-10работ) происходит овладение умениями логико-математического анализа учебного материала учебников в основном для неполной средней школы, подбора вопросов и математических задач как средства обучения конкретному содержанию, организации и управления поиском решения школьных математических задач как цели математической деятельности на школьном уровне и доказательства математических утверждений, составления и оценивания контрольной работы по математике для учащихся и анализа ее результатов.
Вся названная группа учебных и методических умений в значительной мере может быть сформирована без выхода в школу.
Во втором цикле лабораторных работ (4-5 работ) формируются умения наблюдать уроки математики в основном в неполной средней школе, анализировать их, отбирать материал для конкретного урока и составлять развернутые фрагменты урока и целиком конспекты уроков.
Данная группа методических умений связана с подготовкой к проведению уроков на первой активной педагогической практике. На данном этапе в ходе посещения уроков и бесед с учителями необходимо выяснять подходы учителей к определению целей урока, зависимость цели урока от его места в системе уроков, от конкретного содержания учебного материала, от возможностей класса и т. п. Как один из приемов подготовки к постановке урока можно использовать коллективные определения цели того или иного урока во время анализа учебного материала. Это должны быть первые уроки темы. После коллективного определения цели урока или его фрагмента и постановки конкретных учебных задач на этом этапе можно самостоятельно отобрать к уроку учебный материал, средства обучения, формы организации детей на уроке или отдельном его этапе, разработать приемы оценки деятельности учащихся на уроке. Результаты работы на этом этапе выражаются в написании развернутых конспектов уроков или их фрагментов.
В третьем цикле лабораторных работ формируются умения анализировать учебный материал школьных учебников через реализацию в них конкретных математических методов: дедуктивного метода доказательства математических утверждений, координатного метода, векторного метода, метода геометрических преобразований, метода уравнений и неравенств, метода применения производной и интеграла.
Цель данного цикла двоякая. С одной стороны, изучить, какие математические методы и в какой форме реализованы в содержании школьного математического образования. С другой стороны, поскольку названные выше математические методы изучаются в школе на разном материале, а следовательно, в разные годы обучения, то это позволяет анализировать учебный материал (а значит, его осмысливать и усваивать) не только с точки зрения реализации математического метода, но и с точки зрения развития содержания и форм организации учебного материала в учебниках.
В данном цикле возможно вновь возвратиться к логико-математическому анализу учебного материала, но уже с новой методической нагрузкой, отмеченной выше, и с учетом разработки вопроса, как этот материал помогает сформировать тот или иной математический метод и, с другой стороны, как математический метод способствует формированию нового содержания и доказательству новых математических фактов. Приобретенные в первом цикле лабораторных работ учебные и профессиональные умения анализировать конкретный, локального характера учебный материал в данном цикле совершенствуются и развиваются.
Три цикла лабораторных работ, составляющие первый этап обучения учебным и некоторым методическим умениям, завершаются формированием умений выполнять логико-математический анализ различного учебного материала с учетом конкретно поставленных целей, отбора и подготовки некоторых средств и методов обучения.
Второй этап практической подготовки связан с формированием умений целеполагания и отбора учебного материала и средств обучения в соответствии с поставленными целями и сформулированными учебными задачами.
Этот этап состоит из двух циклов. Первый включает в себя практические занятия, направленные на отработку умений ставить цели изучения конкретного материала на уроке в зависимости от его содержания и с учетом возрастных возможностей учащихся. Отрабатываются эти умения обычно на фрагментах содержания начальных тем курсов «Геометрия, 10» и «Алгебра и начала анализа, 10», но в рамках логико-математического анализа темы, куда тот или иной конкретный вопрос входит. При этом формируется еще одно методическое умение - написание развернутого плана урока.
Второй цикл этого этапа наиболее сложный и трудный. Он синтезирует в себе все ранее сформированные умения и решает максимально значимые методические цели. Суть этого цикла заключается в том, что на отдельных темах, существенно значимых в содержательном плане и в то же время достаточно локальных по организации, таких, как «Многоугольники», «Перпендикулярность прямых и плоскостей», «Интеграл» и др., формируются методические умения ставить цель и определять мотивы изучения темы. В соответствии с поставленными целями выполняются логико-дидактический анализ теоретического материала темы и типизация математических задач. Результаты логико-дидактического анализа темы материализуются в составлении подробного тематического плана изучения темы. План содержит разбивку темы на отдельные уроки, к урокам указаны конкретные типы математических задач с учетом обязательных результатов обучения; определены виды самостоятельных работ и формы их проведения на уроках и дома; с целью создания положительной мотивации подобран исторический материал, материал, имеющий практическое и политехническое значение, и др.; определены применительно к конкретным урокам средства обучения, включая ТСО и ЭВМ. К каждому из уроков, приведенных в календарном плане, на основе такого подробного анализа теперь уже возможно поставить цели его проведения и сформулировать учебно-познавательные задачи. К отдельным урокам может быть составлен развернутый план и по нему проведена деловая игра.
На этот цикл отводится наибольшее количество практических (12-15 занятий). Он основной в методической подготовке учителя, так как умение выделять ядерный материал темы, ставить цели для его изучения и отбирать в соответствии с этим средства и методы обучения ―это основные методические умения, которым необходимо обучиться еще в вузе.
Данный цикл реализуется в основном на учебном материале курсов математики IX-X классов в связи с подготовкой к заключительной педагогической практике.
Третий этап тоже включает в себя формирование умений выполнять логико-дидактический анализ учебного материала школьных учебников, но теперь анализируется материал с целью выяснения реализации в учебнике какой-либо математической идеи или линии. Здесь уже принимаются во внимание цели реализации той или иной идеи или линии, используемые для этого формы и методы реализации с учетом развития знаний учащихся и строгости изложения материала. Материалом для реализации такого анализа может служить, например, линия уравнений или неравенств в школьном курсе математики, начиная от V класса и кончая XI. Для анализа четко определяются цели и мотивы изучения выбранной линии в каждом классе, выделяются понятийный аппарат линии, математические методы реализации линии, логические и содержательные обоснования применения того или иного метода, раскрываются сферы применения изученного материала, подбираются средства формирования понятийного аппарата линии и методов применения этого аппарата для самой математики и ее приложений, разрабатывается система оценок достигнутых результатов по изучению линии.
В алгебраической части учебного материала такие линии выбрать не так уж трудно. Это может быть и линия изучения функций, например в X-XI классах, может быть и линия тождественных преобразований в неполной средней школе. В геометрии такую линию или идею определить сложнее. В качестве примера можно предложить линию измерения геометрических величин, которая реализуется от V до XI классов и проходит при этом существенные изменения как по строгости обоснований, так и по конкретным приемам ее реализации.
Таким образом, система лабораторных работ и практических занятий по методике преподавания математики позволяет постепенно усложнять формируемые учебные и методические умения от логико-математического анализа локальных единиц учебного материала до логико-дидактического анализа реализации определенных линий в школьных учебниках на протяжении всего периода обучения.
Так как самой сложной по структуре является система целеобразования, то, естественно, и самым трудным умением является умение разрабатывать систему изучения темы (линии) с учетом достижения конкретных целей. Кроме того, в содержании практических занятий учитываются еще два фактора: 1) раскрытие специфики содержания курсов математики V-VI классов, VII-IX классов и Х-ХI классов. Каждый из этих учебных циклов имеет не только содержательную специфику, но и организационную.
При этом важен учет уровней строгости изложения учебного материала в каждом из циклов; 2) сформированность учебных и методических умений к методической и стажерской педагогическим практикам.
§ 3. МАТЕМАТИЧЕСКИЕ, УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ЗАДАЧИ
Так как учителю в практической деятельности приходится решать различные задачи: математические, учебные и методические, то представляется целесообразным раскрыть сущность всех трех названных выше задач и показать особенности их использования при его профессиональной подготовке.
Математические и учебные задачи. Трактовка понятия «учебная задача» будет более четко выражена, если его раскрывать в сравнении с понятием конкретно-практической (математической) задачи.
Анализ литературы по детской психологии и дидактике (А. Н. Леонтьев, Д. Б. Эльконин, В. В. Давыдов, Г. И. Щукина, Н. Ф. Талызина и др.) показывает, что осмысление понятия «учебная задача» приобретает более конкретный смысл только в концепции учебной деятельности.
Понятие учебной задачи впервые в отечественной литературе появилось в психологических работах, связанных с разработкой концепции учебной деятельности (Д. Б. Эльконин, 1962 г.). Было отмечено, что существенным результатом решения учебной задачи будут изменения, происходящие в субъекте, а не в материале, с которым имеет дело решающий учебную задачу.
В связи с развитием концепции учебной деятельности В. В. Давыдов детализирует сущность этого понятия. В частности, он пишет: «...потребность в учебной деятельности побуждает школьников к усвоению теоретических знаний, мотивы — к усвоению способов их воспроизводства посредством учебных действий, направленных на решение учебных задач (напомним, что задача - это единство цели действия и условий ее достижения).
Учебная задача, которая предлагается школьникам, требует от них: 1) анализа фактического материала с целью обнаружения в них некоторого общего отношения, имеющего закономерную связь с различными проявлениями этого материала, т.е. построения содержательной абстракции и содержательного обобщения; 2) выведения на основе абстракции обобщения частных отношении данного материала и их объединения (синтеза) в некоторый целостный объект, т.е. построения его «клеточки» и мысленного конкретного объекта; 3) овладения в этом аналитико-синтетическом процессе общим способом построения изучаемого объекта» ([59], с. 151, 152).
Следовательно, результатом решения учебной задачи является овладение «общим способом построения изучаемого объекта».
Для раскрытия смысла «общего способа построения изучаемого объекта» в конкретной деятельности учителя весьма плодотворным является использование понятий непосредственного (прямого) продукта учебной деятельности.
Под непосредственным (прямым) продуктом учебной деятельности будем понимать результат деятельности, на достижение которого в данный момент направлены главные усилия учащегося и который определяется основной, ближайшей целью деятельности. Необходимость введения названных понятий объясняется тем, что в процессе учебной деятельности учащийся одновременно решает несколько различных задач: математическую, учебную, познавательную, мыслительную. Но одни из них в конкретной ситуации ведущие, основные. Другие помогают решению основной задачи. и часто выступают в качестве средства решения основной. Естественно, между этими задачами и методами их решения существует очень сложная связь. Мы считаем, что обучение будет более действенно, если четче понимать, какая из задач на каждом конкретном этапе обучения выполняет ведущую функцию, т.е. является прямой (основной, ближайшей, непосредственной ) целью деятельности.
Таким образом, исходя из общего понятия задачи и понятия прямого продукта учебной деятельности можно высказать существенные свойства учебной и математической задач.
Для математической задачи прямым продуктом ее решения будет получение математического факта.
Под математическим фактом будем понимать числа, выражения, формулы, корни уравнения, свойства математических понятии, отношения, используемые в алгебре, геометрии, математическом анализе. Например, быть параллельными. больше или меньше (и их эквиваленты в естественном языке: быстрее, медленнее, короче, длиннее) и т.п.
Решение математической задачи выполняется на основе и с помощью познавательно-мыслительных операций (анализ, синтез, аналогия, сравнение и др.), общих учебных действий (распознавание, получение следствий, действия по актуализации и выбору знаний и др.) и их операций. Но при решении математических задач значительное место занимают специальные (математические) действия и операции (сложение, вычитание, умножение, деление, логарифмирование, приведение подобных членов, разложение на множители и т.п.), а также общие методы, свойственные науке и предмету математики (дедуктивный, координатный, векторный и др.), и конкретные методы решения определенных типов математических задач (метод подобия, метод равных треугольников, метод интервалов и т. п.).
При решении учебных задач прямым продуктом является учебный факт.
Под учебным фактом будем понимать прежде всего знание, но не любое, а на таком уровне обобщения, когда оно в значительной мере выполняет функции метода (приема) обучения или учебного познания. Например, знание определений математических понятий может выступать как математический факт, когда речь идет о конкретном определении конкретного математического объекта (биссектрисы угла, функции, коэффициента и т.п.). Когда же знание определений понятий выступает в теоретической обобщенности, т.е. в понимании смысла существенных свойств в определениях понятий и объектов, структуры определений, учебных действий, связанных с формированием определений понятий, то такие знания выступают уже в функции метода учения и познания и являются прямым продуктом решения учебной задачи.
Другой пример. Кроме определений понятий и объектов, основным компонентом теоретических знаний в школьном курсе математики являются теоремы (свойства, признаки, законы и др.). Чтобы они стали учебными фактами, необходимо их изучить на уровне теоретического обобщения. А это значит, что результатом обучения теоремам должно быть не только знание отдельных теорем, их формулировок и даже доказательств (в этом случае. они выступают как математический факт), но и знание их логической структуры (выяснение структурных общностей в разных теоремах), сущности самого процесса доказательства в математике, основных методов доказательства, применяемых в школьном курсе математики, и др. Такие обобщенные знания выполняют функцию методов обучения и учения, могут быть использованы в аналогичных и новых ситуациях и тем самым служить основой реализации требования реформы о школе ― вооружать учащихся разнообразной технологией учения с целью подготовки их к самообразованию, т.е. учить учеников учиться самостоятельно.
К учебным фактам относятся также обобщенные типы математических задач, общие и специфические, способы их решения, общие приемы поиска доказательства математических утверждении и решения математических задач и др.
Значит, главной особенностью учебных фактов будет направленность их на формирование общих умений учиться самостоятельно, т.е. на овладение умением самостоятельно раскрывать структуру новых знаний (для школьного предмета ― определений понятий и математических объектов, теорем, алгоритмов, математических методов); умением относить конкретную задачу к определенному типу или рассматривать ее как самостоятельное оригинальное явление, требующее для своего решения творческого подхода; умением обнаруживать способ доказательства нового математического утверждения и выполнять его, располагать и владеть набором общих и специфических учебных действий и операций, адекватных поставленной учебной задаче, и др.
Решается учебная задача либо путем обобщения определенных видов теоретических знаний, определений, теорем, алгоритмов, методов, либо путем обобщения решения наборов конкретно-предметных, в нашем случае математических, задач. Основными общеучебными и общепознавательными действиями, используемыми при решении учебных задач, будут сравнение, обобщение, конкретизация, классификация и др. Выполняются и формируются эти действия с помощью и на основе мыслительных операции: анализа, синтеза и др. — и специфических, в нашем примере математических, действий и операций.
Если сравнивать предметные и учебные факты, то между ними есть связь. Например, определение конкретного математического понятия есть математический факт. Но определение понятий есть и учебный факт. Отличие в этих фактах в том, что предметную область интересует само предложение, заключающее в себе отличительные свойства понятия. Но как эти свойства связаны в конкретном определении понятия, тем более так ли они связаны, как и в другом определении другого понятия, какие познавательные следствия из такой аналогии связей свойств, если она есть, можно извлечь, — предметную область чаще всего не интересует, а если и интересует, то не в такой степени, как учебную. Для обучения же, т.е. для процесса получения знании в новой ситуации, а именно в этом смысле важен в конечном счете процесс обучения, ценна именно эта общность в изучаемых объектах предметной области.
Общность эта может быть различной природы: 1) содержательная общность в трактовках различных конкретных вопросов (например, единая содержательная основа в определении понятий функции и уравнения); 2) структурная общность (например, определения биссектрисы угла и параллелограмма имеют одинаковую конъюнктивную связь существенных свойств); 3) общность в структуре рассуждения при доказательстве утверждении и получении выводов (например, доказательство всех теорем существования и единственности, одинаковое по форме рассуждения); 4) общность анализа математических задач определенного типа и т.п.
Чтобы та или иная общность была используема в процессе обучения как метод учения, т.е. стала учебным фактом, средством, используемым при изучении других аналогичных по общности вопросов, она должна быть доведена до теоретического обобщения, осмыслена вне контекста одной конкретно-предметной задачи. Например, при обучении определениям понятий и объектов учащийся в конечном счете должен знать, что такое существенное свойство понятия вообще, сколько и какие из них могут быть включены в определение и в какой взаимосвязи. Учет последнего факта влияет на применение определений при классификации объектов. Владея этими знаниями как приемами учения и используя их при изучении других определений понятий, учащийся убеждается, что различных по структуре определений понятий в школе не так уж и много. Значит, и подход к их изучению при различном предметном содержании может быть одинаков по логике раскрытия их структуры по учебным действиям, по методу.
Таким образом, различие между учебной и математической задачами идет в основном по пути теоретического обобщения с точки зрения процесса учения. В каждой предметной области это может быть содержательная, логическая или процессуальная обобщенность. Оснащая ученика, во-первых, знанием этой обобщенности, а во-вторых, приемами ее использования, мы создаем ученику возможность быть более уверенным в познании новых фактов, так как он владеет в какой-то мере «инструментами» работы с этими новыми фактами.
Особенную трудность представляет вычленение учебной задачи при решении математических задач. Часто в методической литературе конкретную математическую задачу называют учебной.
Чтобы определить в связи с обучением решению математических задач, какая учебная задача будет при этом решаться, необходимо уточнить ряд понятий: «тип математической задачи», «метод решения математических задач», «сформирован или нет метод решения математических задач».
Проблема типизации математических задач прошла много этапов в своем развитии. Мы не будем здесь анализировать ее, а отметим только, как мы ее будем понимать в данной работе. В один тип предметных (математических) задач, в частном случае, например, алгебраического характера, объединяем задачи, основой решения которых будет какая-то одна математическая теория. Например, тип задач на логарифмические уравнения, на тождественные преобразования рациональных выражений, задачи на исследование квадратичной функции, сюжетные задачи на движение и др. Внутри типа может быть более детальная типизация, которая может определяться, например, приемами решения, специфическими учебными действиями, приемами поиска решения задач и т.п. Типизация геометрических задач более сложна, хотя подходы к типизации на основе теоретических знаний, в них заложенных, тоже могут быть применены.
С методами решения задач определенного типа связаны соответствующие ему действия:
1) специфические, для нас — математические. Например, действия по использованию прямого или косвенного доказательства математических утверждений, действия по применению координатного метода, действия по применению «метода интервалов» при решении неравенств и т.п. Математические действия в процессе их выполнения и в зависимости от поставленной задачи конкретизируются. В примере косвенного доказательства это, например, операция построения отрицания утверждения, операция получения следствий из системы связанных утверждений и т.п.;
2) учебно-познавательные. Например, моделирование основного отношения математической задачи, конкретизация приема для рассмотрения определенной математической задачи и др.
Итак, метод решения математических задач определенного типа есть свойственная данному типу задач взаимосвязь учебно-познавательных и математических действий.
Ответ на вопрос «Сформирован метод или нет?» будет заключаться в умении анализировать учащимися собственные действия, адекватные действиям, составляющим содержание метода. Результативным методическим приемом определения сформированности метода будет «решение» математических задач типа с недостающими данными или анализ «решения» математических задач, в которых допущена ошибка.
Для того чтобы на конкретном примере раскрыть отличие математической задачи от учебной, необходимо выяснить, можно ли на основе одной математической задачи раскрыть метод решения типа математических задач. Покажем это на примере обучения решению иррациональных неравенств.
В состав метода решения иррациональных неравенств
входят следующие действия: анализ на основе синтеза условия задачи; действие
конкретизации сравнения имеющихся теоретических знаний и знаний, полученных в
результате выполненного анализа условия конкретной задачи; действие
представления множеств решения неравенств, их систем и совокупностей на
координатной прямой. Действия, свойственные только методу решения
иррациональных неравенств, следующие: приемы установления области определения
функций вида ![]() и определение знака их значения;
«уединение» радикалов в одну часть неравенства и возведение обеих частей
неравенства в соответствующую натуральную степень; использование логических
условий образования системы или совокупности уравнений и неравенств; решение
линейных и квадратичных уравнений, неравенств, их систем и совокупностей.
и определение знака их значения;
«уединение» радикалов в одну часть неравенства и возведение обеих частей
неравенства в соответствующую натуральную степень; использование логических
условий образования системы или совокупности уравнений и неравенств; решение
линейных и квадратичных уравнений, неравенств, их систем и совокупностей.
Для раскрытия наиболее существенных действий метода решения иррациональных неравенств предлагаем «хорошую» С точки зрения раскрытия метода математическую задачу.
3адача. Решить неравенство ![]() .
.
1. Анализ условия и требования задачи приводит к
необходимости выполнения математического действия ― установления области
определения функций ![]() .
.
![]() Для одного и того
же неравенства необходимо получить пересечение
Для одного и того
же неравенства необходимо получить пересечение ![]() и
и ![]() , т. е. имеем
, т. е. имеем ![]() .
.
Решив систему линейных неравенств , получаем
первоначальную область задания неравенства ![]() .
.
2. После конкретизации теоретических знаний о
существовании и неотрицательности функции выясняем, при каких условиях функции ![]() и
и ![]() существуют и
неотрицательны.
существуют и
неотрицательны.
После этого возводим обе части неравенства во вторую степень:
![]()
![]()
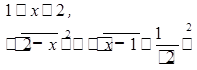
![]()
 (1)
(1)
Повторив первое и второе действия для новой функции и
неравенства (1), получим систему неравенств 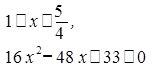 .
.
3. Для решения полученной системы неравенств надо решить квадратичное неравенство. В результате его решения имеем
![]()
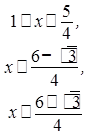 .
.
4. После интерпретации решения системы и совокупности неравенств на координатной прямой получим ответ
![]() .
.
Если сравнить действия, которые входят в состав метода решения иррациональных неравенств вообще, и действия, которые были применены для решения приведенной задачи, то они совпадают. Значит, раскрыть необходимые действия на «хорошей» задаче возможно. Но метод должен быть не только раскрыт, но и сформирован для определенного типа математических задач. А это значит, что в содержании деятельности, направленной на раскрытие метода должны быть знания и действия, раскрывающие тип задачи и адекватные ему действия. Все представительство типа одной задачей не может быть исчерпано. Такие действия, как конкретизация и моделирование, специфичные методу, тоже на одной задаче не могут быть раскрыты и сформированы. На одной задаче нельзя осознать метод.
Итак, для формирования метода решения определенного типа математических задач требуется набор задач. Набор может быть организован по индуктивному принципу обобщения. Например, в нашем случае он может быть следующий:
Решите неравенства:
Набор может быть построен по принципу дедуктивного обобщения.
Решите неравенства:

Найдите ошибку в «решении» неравенства:
4.![]()
Ответ: ![]() .
.
Работа с наборами математических задач в каждом из приведенных случаев различна. В первом случае тип математических задач формируется путем последовательного накопления существенных характеристик типа. Действия, адекватные методу, тоже накапливаются постепенно, и метод будет раскрыт только после решения задач всего набора. Говорить об его сформированности, наверное, с полной определенностью нельзя.
Во втором случае существенные характеристики типа могут быть раскрыты при анализе первой задачи набора. действия, составляющие метод, тоже могут быть раскрыты при поиске решения первой задачи. Последующие задачи второго набора направлены не столько на раскрытие типа, хотя это полностью не снимается, сколько на отработку метода, т. е. на установление взаимосвязей общих и специфических учебных действий метода.
Существенно важной при решении набора математических задач является установка учителя. Если при решении задач из набора обобщался тип задачи: 1) по содержанию математических знаний; 2) по действиям, необходимым для решения задач данного типа; 3) по учебным приемам отнесения конкретной задачи к типу, то в результате такой деятельности учащийся накапливал учебные факты (учебные умения). Посредством активного усвоения общих ориентиров типа математических задач и последовательности специфических и общих учебно-познавательных действий школьник учится решать не только каждую конкретную математическую задачу (получает математический факт), но и целый тип, а значит, решает учебную задачу.
Значит, учебная задача в случае решения математических задач — это такая задача, цель решения которой получить: 1) теоретическое обобщение математических задач определенного типа и 2) метод решения математических задач данного типа, который определяется взаимосвязью специфических и общих учебно-познавательных действий, т.е. обучаемые овладевают общим способом решения всех частных задач определенного типа.
Формулируются учебные задачи обычно в следующем виде: «Раскрыть характеристики типа математических задач...», «Выделить специфические учебные действия для решения типа математических задач...», «Раскрыть компоненты учебного действия «делать вывод...», «Систематизировать действия конкретизации при решении задач типа...» и т.п.
В формулировках учебных задач важны конкретные указания вида «раскрыть характеристики», «выделить действия», «систематизировать операции определенного действия» и т.п. Задача ориентирует на раскрытие конкретных учебных действий, с помощью которых будет достигнута цель задачи. В противном случае их постановка не вносит ничего нового в практику обучения, так как ничем не будет отличаться от формулировки целей обучения.
Возвращаясь к определению учебной задачи, данному в свое время Д. Б. Элькониным. убеждаемся, что действительно в результате решения такой задачи ученик приобретает умение анализировать структуры определений понятий, выполнять доказательство математических утверждений, выделять действия для решения определенных классов математических задач.
Принятая нами трактовка учебной задачи, учебного факта, учебного действия позволяет использовать учебную задачу как основу организации деятельности учащихся на уроке и в домашней работе.
Функция учебной задачи как организатора деятельности учащихся в следующем:
1. Если учебная задача сформулирована четко, то сразу же прогнозируется результат ее решения — обобщенные до уровня метода знания, которые можно будет использовать в аналогичных и новых ситуациях.
2. Для формирования обобщенных знаний до уровня метода необходима определенная организация учебного материала. Так как основным средством организации деятельности учащихся при изучении математики являются математические задачи, то существенную роль играет определение набора задач либо выбор типичной задачи.
3. Если наборы задач будут решаться без установки на обобщение, то даже в случае хорошей их систематизации они не смогут в полной мере выполнить роль средства формирования знаний, обобщенных до уровня метода. Значит, должны быть спланированы общие и специфические учебные действия, с помощью которых формируются обобщенные знания.
4. Процесс деятельности по формированию обобщенного знания будет только тогда закончен, когда учащийся способен оценить свои результаты. Причем в оценку деятельности должны входить не только полученные математические факты, но и учебные результаты, т.е. умение организовать учебный материал, умение наметить план решения математической задачи, умение проверить свои конкретно-предметные действия и др.
Таким образом, при решении учебных задач и организации деятельности учащихся для их решения необходимо соблюдать следующие требования: четко прогнозировать учебный результат, планировать учебный материал для достижения учебного результата, подбирать соответствующие учебные действия и оценивать получение не только математических, но и учебных фактов.
Организующая функция учебных задач в значительной мере зависит от той широты обобщенности, которую предполагает решение учебной задачи. Поэтому учебные задачи можно классифицировать по широте обобщенности. Например, может быть учебная задача, направленная на обучение определениям вообще. Эту учебную задачу ученик решает на протяжении всех лет обучения в школе. Естественно, она должна быть разбита на подзадач и: в зависимости от математического содержания, от их логической структуры, от того, определяется понятие или конкретный объект, и т.п. Аналогично можно решать учебные задачи по обучению теоремам, решению математических задач.
Методические задачи. Кроме математических и учебных задач, учитель математики в своей деятельности часто имеет дело с методическими задачами. Чтобы ответить на вопрос «Что такое методическая задача?», обратимся опять к понятиям «задача» и «прямой продукт деятельности».
Так как задача — это цель в определенных условиях, то целью решения методических задач будет овладение теми методическими умениями, которые были отмечены в § 1. Прямым продуктом решения методических задач будет получение методических фактов: выделение ядерного (основного) и второстепенного учебного материала; типология математических задач; учебный материал, организованный в определенную систему в соответствии с поставленной целью; отобранные средства и приемы обучения для достижения поставленной цели и др.
Как всякая задача, методическая задача решается с помощью определенных действий и операций. Первой и существенной особенностью методических действий есть их согласованность с целью деятельности в целом и конкретной методической задачей в частности. Например, может быть поставлена методическая задача: «Типизировать математические задачи по теме «Площади фигур» с целью систематизации общих приемов поиска решения геометрических задач в итоговой теме курса планиметрии».
При изучении этой же темы и в том же месте могут быть поставлены и другие методические задачи. Например: «Типизировать математические задачи по теме «Площади фигур» с целью более эффективного обучения решению задач данной темы» или «Типизировать математические задачи по теме «Площади фигур» с целью обучения приему поиска решения математических задач «методом площадей» и др.
Каждая из поставленных методических задач требует своих, адекватных ей методических и учебных действий. Для решения первой задачи необходимы чтение и анализ методической литературы и анализ учебного материала по теме «Площади фигур» по учебнику с целью составления набора общих приемов поиска решения математических задач вообще и геометрических в частности. Из полученного набора необходимо отобрать приемы наиболее приемлемые, учитывая результаты анализа темы «Площади фигур». В теме есть задачи алгоритмического характера, т.е. задачи на непосредственную подстановку данных в формулу площади той или иной фигуры; есть задачи с заданием найти площадь фигуры, формула площади которой известна, и тем самым первый шаг поиска решения задачи уже как-то определен, но в процессе дальнейшего решения необходим поиск для нахождения какого-нибудь элемента в формуле площади фигуры. Есть задачи для выбора первого шага решения, в которых необходим предварительный глубокий анализ условия и заключения задачи и сопоставления полученных данных с известными фактами из теории и известными приемами решения задач и др.
Так как тема итоговая в курсе планиметрии, то сюжеты задач заключают в себе сведения почти из всего курса. Естественно в данной теме осуществить и систематизацию приемов поиска решения задач в планиметрии. На основе выделенных приемов можно получить некоторую типологию задач. В решении данной методической задачи наблюдается определенная согласованность общих целей обучения решению математических задач (типизация математических задач и нахождение общих приемов поиска решения задач определенных типов) со спецификой обучения решению задач конкретной темы. Такого типа методические задачи следует считать наиболее продуктивными, так как они придают процессу обучения обобщенность и систематичность, а именно такой подход обеспечивает более глубокое изучение предмета и формирование необходимых качеств личности обучающегося.
Решение второй методической задачи, которую возможно поставить при изучении темы «Площади фигур», имеет более значимые результаты для процесса обучения в целом и геометрии в частности, так как ее можно решить, не анализируя литературу; с целью отбора приемов поиска решения математических задач не требуется выделения приемов, специфичных для данной темы. Решение этой методической задачи может ограничиться анализом только самой темы по учебнику. Любой результат типизации будет более эффективным, чем полное его отсутствие.
Еще более узкий результат будет при решении третьей, названной ранее методической задачи. Он может быть сведен к выделению типа математических задач, решаемых «методом площадей», т.е. задач, в условии которых нет явных сведений о площади фигуры, но решать их надо на основе использования площади одной или двух фигур, данных в условии задачи.
Как мы уже отмечали ранее (§ 1), методические и учебные умения в определенной своей части, связанной с учебной деятельностью, имеют много общего; поэтому и результаты их решения подчас бывает трудно разделить. В практической деятельности в этом и нет необходимости. Поэтому такие задачи и в теоретическом плане лучше называть учебно-методическими. Это задачи, направленные на формирование умений целеполагания, мотивации и оценки деятельности учащихся.
Однако есть задачи, продукт решения которых есть непосредственно методические факты. К таким задачам можно отнести подбор учебного материала и других средств обучения; организацию материала в определенную систему для достижения поставленной цели, для организации самостоятельной работы учащихся и др. для решения таких задач необходимы методические действия. В основе методических действий лежат учебно-познавательные действия — только теперь они выступают в более обобщенной форме и во взаимосвязи нескольких действий одновременно. Так, например, чтобы выполнить отбор средств для обучения какому-либо вопросу, необходимы действия целеполагания и мотивации обучения, отбор действий, адекватных изучаемому вопросу, знания функций различных средств обучения и их соответствие определенному содержанию и учебным действиям и т.п. И все эти действия необходимо выполнять последовательно, одно за другим, и применение каждого из них обязательно. Если не поставлены цели, не будет результативного отбора задач; если не определены действия, неясно, какие же задачи отбирать, и т.п. Таким образом, существенной характеристикой решения методических задач является комплексность разного содержания действий.
Ниже при разработке конкретных лабораторных работ и практических занятий будет дана методика постановки и решения соответствующих методических задач.
Итак, учителю в практической деятельности приходится решать различные задачи: математические, учебно-познавательные, учебно-методические, методические. Все эти задачи имеют много общих моментов в их постановке, в действиях для их решения и даже в результатах решения, но каждая из них имеет и свои специфические особенности. В практической деятельности следует в каждом конкретном случае учитывать их специфику и там, где есть необходимость, вскрывать общности. Такой подход к использованию различных по учебным функциям задач в обучении позволит учителю конкретнее видеть, какого результата в той или иной ситуации он от учащихся добивается и что в тот или иной момент деятельности следует оценивать.
Глава II
ЛАБОРАТОРНЫЕ РАБОТЫ ПО МЕТОДИКЕ ПРЕПОДАВАНИЯ МАТЕМАТИКИ
§ 4. ОСНОВНЫЕ КОМПОНЕНТЫ СОДЕРЖАНИЯ УЧЕБНОГО МАТЕРИАЛА ПО МАТЕМАТИКЕ В ШКОЛЕ И ИХ ЛОГИКО-МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Как было сказано в главе I, только на основе профессиональных умений можно осуществлять профессиональную деятельность. Один ее, но основной аспект — подготовка к уроку — включает в себя умения выполнять анализ учебного материала, планировать его изучение, обосновывать выбор средств обучения, изготавливать наглядные пособия, контролировать и оценивать учебную деятельность учащихся и результат учения. Система этих умений формируется в первом цикле лабораторных занятии.
Прежде чем раскрыть сущность основного профессионального умения — логико-математического анализа содержания учебного материала по математике, - необходимо уточнить, что будем понимать под понятием «содержание учебного материала».
Под содержанием учебного материала в разных литературных источниках понимаются иногда разные объекты. Иногда это идеи, факты, математические задачи. Иногда это конкретные тексты учебников и математические задачи. Тексты разбиты на пункты. Каждый пункт изучается в течение 2-3 уроков, провернется его усвоение. Затем переходят к следующему пункту. В конце темы — итоговая контрольная работа.
В таком случае каждый пункт и параграф учебника можно анализировать как новое, оригинальное содержание и анализ сводить к выяснению, о чем же в той или иной порции материала идет речь. Такой подход возможен, он бытует в практике школы, но на его основе трудно осуществить обобщение содержания и установление внутрипредметных связей. Что и приходится часто наблюдать в школе.
Если анализировать знания на основе сущности процесса усвоения, т.е. идти от знаний-знакомств к фундаментальным знаниям затем к методологическим знаниям и, наконец, к знаниям-умениям, определяющим практическое владение предметом, то в математике часто будут пересечения первых трех видов в силу абстрактности предмета, когда знания сразу несут в себе и фундаментальную, и методологическую сущность.
Нам представляется, учитывая специфику предмета математики (абстрактность понятий и логическая доказательность утверждений), в содержании учебного материала можно вычленить два крупных блока: теоретический материал и математические задачи. Теоретический материал с методологической точки зрения (с точки зрения форм познания) представлен понятиями и их определениями: утверждениями (теоремы, свойства, признаки и т.п.), алгоритмами (правилами, формулами и др.) ,различными по степени общности и предметному содержанию математическими методами (аксиоматическим — прямое и косвенное доказательство, координатным, векторным, методом уравнений и неравенств, методом равных треугольников, методом подобия и др.).
В конкретных темах школьного предмета эти компоненты представлены во взаимосвязи. Взаимосвязь определяется либо принципами построения дедуктивной теории, адаптированными для школы (так чаще всего бывает в курсе геометрии), либо содержательными идеями, интерпретированными для конкретной темы предмета (идея расширения числа, идея расширения возможностей выполнения тождественных преобразований и т.п.).
Математические задачи тоже можно разделить на две группы по способу их использования в учебном процессе, Это — математические задачи, которые используются для формирования понятий, непосредственного применения изученных утверждений, закрепления алгоритмов (и в этом случае их будем называть упражнениями), раскрытия и непосредственного применения математических методов. Задачи с названными функциями чаще всего не требуют специальной деятельности (аналитико-синтетической) для поиска их решения, результат их решения обычно находится в один-два хода, но он важен бывает для иллюстрации какого-нибудь свойства понятия или особых условий применения утверждения, алгоритма или метода. Такие задачи методисты обычно называют задачами как средством обучения математике. Такие задачи сейчас преобладают в школьных учебниках.
В содержании учебного материала должны существенное место занимать математические задачи, на основе которых возможно организовать математическую деятельность на школьном уровне: постановку задачи и ее принятие, организацию поиска решения (анализ условия задачи; сопоставление условия и известных математических фактов, включая и приемы решения задач; выработку стратегии решения и составление плана решения задачи), реализацию плана, критическое осмысление результатов решения и др.
Кроме названных компонентов содержания (теоретические знания и математические задачи), можно указать еще факты, которые не есть теоремы, или определения, или алгоритмы, так как они не удовлетворяют тем трактовкам теоремы, определения или алгоритма, которые приняты в методической литературе и учебниках. Обычно это теоремы, но в учебнике они не доказываются. Это дидактическая проблема, и ее надо рассматривать с учетом концепции, принятой автором того или иного школьного учебника. Такие факты либо постулируются учебником и иллюстрируются картинкой, либо являются результатом решения задачи. Эти факты следует относить к теоремам с оговоркой, что эти утверждения где-то доказаны.
Такая трактовка учебного материала позволяет в любом разделе текста учебника выделить определения понятий или объектов, проанализировать их логическую структуру и генезис образования, установить логические, а если возможно, и математические общности или различия, что способствует разработке более эффективной как по времени, так и по содержанию методики обучения математике в целом, а также отдельных ее тем.
При таком подходе может стоять, например, большая учебная задача: научить анализировать структуру определений понятий и объектов. Задача эта вполне разрешима, так как в школьных учебниках встречается не более 4-5 видов определений понятий и объектов.
Аналогично можно подойти к изучению теорем, алгоритмов и т.д. Поэтому, прежде чем разрабатывать методику обучения конкретного содержания тем курсов, необходимо научиться понимать логическую структуру и математическое содержание основных его компонентов и связей между ними.
Первый цикл лабораторных занятий направлен на раскрытие логической структуры и математических трактовок каждого из компонентов отмеченного выше содержания.
Логико-математический анализ не предполагает формулировку целей изучения того или иного компонента содержания, так как это возможно сделать только после определения целей изучения темы, а такая работа будет проводиться позднее. Этот анализ не предполагает и выяснения контролирующих действий. Естественно, авторы учебников, отбирая учебный материал и организуя его в определенную последовательность, выполняли эту работу с определенной общей социальной и познавательной целью. Эта цель сформулирована в программе. И для выполнения логико-математического анализа учебного материала достаточно понимания и знания этих целей. Логико-математический анализ учебного материала — это как бы чтение школьного учебника внимательными и грамотными глазами учителя. «Читая» так учебник для определенного класса, учитель должен ответить себе на ряд вопросов: какие новые понятия, объекты вводятся? Даются ли им определения? К какому по структуре виду определений можно отнести данное определение? Встречались ли ранее определения с такой структурой или мы имеем дело с новой структурой? Какие познавательные и учебные действия можно выполнять для раскрытия структуры определения и его применения? Какой возможен содержательный материал для раскрытия всех операций и действий? Ответы на все эти вопросы и позволят сделать вывод о логической структуре определения понятия или объекта.
Ответы на вопросы, какая математическая идея лежит в основе фундаментальных определений, группы определений конкретной темы, раздела учебника или отдельного определения, какие математические действия возможны с теми или иными математическими объектами, как обосновываются те или иные свойства объекта или понятия, какие возможны трактовки. определяемых понятий, какие математические задачи могут раскрыть наилучшим образом то или иное понятие, позволяют установить математическое содержание учебного материала.
В случае выполнения логико-математического анализа утверждений необходимо выяснить их структуру и установить, были ли ранее утверждения с аналогичной структурой, простая или сложная теорема, верно ли обратное утверждение к данной теореме и тем самым не будет ли данное утверждение признаком понятия и т.д.
Выполняя логико-математический анализ учебного материала, необходимо выяснить обоснованность математических доказательств.
Только выполнив логико-математический анализ основных компонентов учебного материала школьных учебников, можно приступать к разработке методики обучения понятию, разделу учебника, теме и т. п. и формировать следующую группу учебно-методических умений.
§ 5. ЛАБОРАТОРНЫЕ РАБОТЫ ПО ЛОГИКО-МАТЕМАТИЧЕСКОМУ АНАЛИЗУ ОСНОВНЫХ КОМПОНЕНТОВ УЧЕБНОГО МАТЕРИАЛА
Лабораторная работа №·1
Тема. Логико-математический анализ определений понятий и объектов, основные этапы их формирования.
Цели. 1. На основе систематизации теоретических знаний о видах и структуре определений понятий и объектов и анализа школьных учебников математики раскрыть логико-математическую структуру типичных для школьного курса математики определений понятий и объектов.
2. Сформулировать основные учебные задачи, которые необходимо решать при формировании математических понятий и объектов, и адекватные им 'учебные действия.
3. Раскрыть на конкретных примерах основные этапы изучения математических понятий в школе.
4. Раскрыть математическую трактовку некоторых фундаментальных понятий курса математики, подобрать из литературы или школьных учебников другие трактовки одних и тех же математических понятий.
5. Подобрать возможные средства, с помощью которых раскрывались бы структура определений и их математические трактовки.
Оборудование. 1. Диафильм «Функция», авт. Е. Арутюнян, 07-3-513.
2. Диапозитивы: «Основные понятия геометрии», авт. М. Антоновский и М. Волович, Б4-20-008; «Десятичные дроби», авт. Э. Красс, 54-20-019.
3. Кодопозитивы с изображением структур определений, таблиц для выполнения действия подведения под понятия.
4. Задания для отработки конкретных этапов формирования определений.
Основное содержание
1. Определение математических объектов и виды определений
Вопрос о понятиях, объектах и их определениях очень сложный по содержанию и может рассматриваться с разных точек зрения:·логической, содержательной (предметной), познавательной (гносеологической) и др., и в силу этого даже в разных методических пособиях даются разные его аспекты. Мы считаем, что в качестве основы необходимо выбрать логическую структуру с учетом математических трактовок. Учитывая, что обучение возможно только в деятельности, необходимо рассматривать действия, адекватные видам определений понятий и объектов. Поэтому в содержание работы будет входить актуализация и систематизация знаний по смыслу операции «определение понятий», структуре определений (def) и их видов.
Задание 1. Актуализируйте и систематизируйте знания по понятиям и их определениям, ответив на следующие вопросы:
1) Что такое понятие, объект? В чем их сходство и различие?
2) Существенные и несущественные свойства понятия. Приемы их установления.
3) Содержание и объем понятия. Связь между ними.
4) Логическое действие «определение понятий». Дефиниция.
5) Виды определений понятий и объектов, которые чаще всего встречаются в школе.
6) Структура определений понятий и объектов.
7) Основные требования к определениям понятий.
Основным итогом работы будут следующие факты:
Понятие — это форма мышления о целостной совокупности существенных и несущественных свойств объектов реального мира, в частности и математических объектов. Для формирования математических понятий необходимо понимание математического объекта, который в понятии характеризуется благодаря применению определенных умственных действий.
Когда ведется речь о математическом объекте, например о ромбе или квадратном уравнении и т.п., то имеется в виду конкретный эмпирический (реальный) объект, представленный в виде рисунка, модели или аналитической записи, и одновременно теоретический (идеальный) объект, обладающий всеми существенными свойствами. В примере с ромбом это не только нарисованный ромб, но и все объекты, которые суть геометрические фигуры с четырьмя сторонами, противоположные из которых параллельны. все стороны равны, диагонали перпендикулярны и т.п.
Сформировать понятие об объекте — это значит раскрыть все существенные свойства объекта в их целостной совокупности. Деятельность ученика (субъекта) при этом направлена на изучение математического объекта, а продуктом этой деятельности будет правильное понятие.
Одним из действий изучения математического объекта для получения понятия о нем является действие определение.
Определить объект — это значит выбрать из его существенных свойств такие и столько, чтобы каждое из них было необходимо, а все вместе достаточны для отличия изучаемого объекта от других.
Выполняется действие определения различными путями (с помощью различных мыслительных и предметных операций), и результат его выполнения фиксируется в различного вида определениях.
Логическая структура действия определения математических объектов, вообще говоря, едина.
Сущность действия определения математических объектов. Для понимания сущности действия определения математических объектов необходимо понимание структуры аксиоматически построенной теории. Если учебный предмет строится аксиоматически (или близко к аксиоматическому методу), то выбираются основные объекты (фигуры) и их существенные свойства или связи между ними раскрываются в системе аксиом. Так, в учебнике А. В. Погорелова ([113]) основные фигуры в планиметрии «точка» и «прямая» и отношения между ними «принадлежать» и «лежать между» раскрываются с помощью четырех аксиом.
Затем на основе косвенно охарактеризованных свойств основных объектов (фигур) предмета и отношений определяются последующие объекты (фигуры) предмета.
Например, луч уже можно определить через введение фигур «прямая» и «точка» и отношение «лежать по разные стороны» как эквивалентное отношение «лежать между» и общие гносеологические понятия «части» и «множество».
Для конструирования определения фигуры «луч» на прямой выбирается ее часть. Часть эта состоит из таких точек, которые лежат по одну сторону от фиксированной точки на прямой, которую называют началом луча. Так как луч — часть прямой, то более широким понятием для него будет прямая; значит, прямая — родовое понятие, причем ближайшее. Видовые отличия: часть прямой; точка ограничивающая эту часть с одной стороны.
Рассмотрим еще пример. Угол — это фигура, которая состоит из двух различных лучей с общей начальной точкой. Родовым ближайшим объектом будет фигура; видовые отличия: два луча и общее начало у этих лучей.
Операции, раскрывающие действие определения объектов, будут следующие: выбирается ближайший родовой объект (фигура), затем на этот объект накладываются как бы ограничения, видовые характеристики (отличия). На основе видовых характеристик (отличий) вводится новый объект, но с меньшим объемом, чем родовой, так как у него больше свойств. Вот этому объекту с большим числом свойств и меньшим объемом присваивается новое название (термин).
Так, из всех равенств уравнением назовем только такие
равенства, в записи которых есть переменные (буквы). Из всех уравнений
квадратными назовем такие, которые имеют вид ![]() где х — переменная; a, b и с —
некоторые числа, причем
где х — переменная; a, b и с —
некоторые числа, причем ![]() . Из всех
прямоугольников квадратом назовем такие прямоугольники, у которых смежные
стороны равны, и т.п.
. Из всех
прямоугольников квадратом назовем такие прямоугольники, у которых смежные
стороны равны, и т.п.
Структура этого действия может быть символически выражена следующим образом:
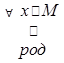
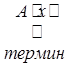

При выделении видов определений математических объектов часто вот это общее действие — определение объектов — называют конкретным видом «определения через ближайший род и видовые отличия». Нам представляется более правомерным вести речь о специфике действий по выделению видовых отличий и в зависимости от этого различать определения и называть их определениями объектов конкретного вида.
В соответствии с этим можно назвать следующие виды определений математических объектов в зависимости от специфики действий, с помощью которых выделяют родовые объекты и видовые отличия. Иначе можно еще сказать, что определения через ближайший род и видовые отличия имеют следующую конкретизацию: 1) определения объектов путем указания их характеристического свойства; 2) отрицательные определения. И отдельно следует назвать неявные определения основных (исходных) объектов (фигур) предмета через систему аксиом; 3) конструктивные и рекурсивные определения.
Определение математических объектов путем описания характеристического свойства. Этот вид определений построен на логических действиях и операциях установления ближайшего рода, видовых отличий и логической природы связи между родом и видовыми отличиями. В зависимости от логической природы связи свойств в школьном курсе математики различают конъюнктивные и дизъюнктивные определения.
Рассмотрим, например, определение параллелограмма. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
Термин — параллелограмм.
Род — четырехугольник.
Видовые отличия: 1) одна пара противоположных сторон параллельна; 2) другая пара противоположных сторон параллельна.
Все свойства в определении соединены союзом «и»; значит, имеем конъюнктивное определение.
Другой пример — определение неправильной дроби.
Дробь, в которой числитель больше знаменателя или равен ему, называется неправильной дробью.
Термин — неправильная дробь. Род — дробь.
Видовые отличия: 1) числитель больше знаменателя; 2) числитель равен знаменателю.
Видовые отличия соединены союзом «или». Определение дизъюнктивное.
Третий пример — определение возрастающей функции.
Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Род — функция.
Термин — возрастающая функция на промежутке.
Видовые отличия: если ![]() Определение по форме записано в виде
импликации.
Определение по форме записано в виде
импликации.
Его можно переформулировать следующим образом:
Видовые отличия: 1) ![]() , и 2)
, и 2) ![]() , и 3)
, и 3) ![]() . Можно оставить
только два самостоятельных свойства:
. Можно оставить
только два самостоятельных свойства:
1)![]() и 2)
и 2) ![]() .
.
Определения такого вида или приводимые к ним составляют подавляющее большинство курса.
Конструктивные и рекурсивные определения. Свойства объекта в таком определении раскрываются путем показа операций его конструирования, т.е. его видовые отличия заданы в виде действий.
Пример 1. Поворотом около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении.
Термин — поворот.
Род — движение.
Видовые отличия: 1) каждый луч. исходящий из точки, повернуть в одном и там же направлении; 2) каждый луч повернуть на один и тот же угол.
Пример 2. Линейной функцией называется функция.
которую можно задать формулой вида ![]() где x —
независимая переменная; k и b — числа.
где x —
независимая переменная; k и b — числа.
Термин — линейная функция.
Род — функция.
Видовые отличия: х — независимая
переменная; k
и
b — числа и ![]() т.е. если эти действия между числами и
переменной заданы, то имеем линейную функцию. Если действия другие, то нет
линейной функции.
т.е. если эти действия между числами и
переменной заданы, то имеем линейную функцию. Если действия другие, то нет
линейной функции.
Конструктивные действия могут задаваться различно. Так, в рекурсивных определениях указываются некоторые базисные объекты некоторого класса и правила, позволяющие получить новые объекты этого же класса.
Например, определение арифметической прогрессии.
Арифметической прогрессией называется последовательность, в которой каждый член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.
Род — последовательность.
Термин — арифметическая прогрессия.
Видовые отличия: ![]() — дан;
— дан; ![]() (в общем виде
(в общем виде ![]() ) — дан;
) — дан; ![]() .
.
Действия получения последующего члена, если известен предыдущий, указаны в видовых отличиях.
Отрицательные определения. Отрицательные определения не задают свойства объекта. Они выполняют как бы классификационную функцию. Если класс объектов разбит на группы (множества) и объектам одной группы, обладающим определенными свойствами, присвоен термин и есть объекты, которые принадлежат этому классу, но отмеченными свойствами (всеми или частью) не обладают. то таким объектам дается отрицательное определение.
Пример. Скрещивающиеся прямые — это такие прямые, которые не принадлежат плоскости и не пересекаются.
Термин — скрещивающиеся прямые.
Род — прямые.
Видовые отличия: 1) не принадлежат одной плоскости; 2) не пересекаются.
Таким образом, логическое действие — определение объекта везде одинаково, но содержательные (математические) действия в каждом из отмеченных видов определений различны. В одних видовые отличия перечисляются как описательные характеристики (быть параллельными, быть больше и т.п.); в других указываются действия, которые надо произвести, чтобы получить (сконструировать) объект; в третьих перечисляются свойства, которые отрицаются.
Таким образом, главное в типологии школьных определении по видам — это понимание специфики действий, раскрывающих (характеризующих) видовые отличия.
3адание 2. На основе актуализированных знаний об определениях математических объектов и их видов выберите из различных школьных учебников: математики, алгебры и геометрии — по 2-3 определения объектов названных выше видов и результаты оформите в таблицу (табл. 2).
Таблица 2 (кодопозитив)
|
Определение путем описания характеристического свойства |
Конструктивное определение |
Отрицательное определение |
Неявное определение исходных понятий |
|
1) Уравнение (V кл.) 2) Ромб (VIII кл.) |
1) Симметричные фигуры относительно точки О (VI кл.) 2) Модуль числа (VI кл.) |
1) Иррациональные числа (VIII кл.) |
Точка и прямая (VII кл. по учебнику А. В. Погорелова) |
II. Основная учебная задача при обучении определениям математических объектов
Основной учебной задачей при обучении определениям математических объектов будет формирование логического действия по раскрытию структуры определения математических объектов и действий, адекватных конкретному виду определений.
действия, с помощью которых будет решаться эта основная учебная задача, следующие:
- логический анализ структуры определений разного вида (выделение логической и содержательной функций каждого слова в определении объекта, отыскание лишних слов в определениях и др.);
- подведение конкретного математического объекта под определение;
- приведение конкретного примера, объекта, иллюстрирующего принадлежность его данному определению;
- замена определения объекта эквивалентным определением этого объекта. Иногда это действие называют переформулировкой определения. Сравнение различных определений одного и того же объекта;
- получение следствий из факта, что объект принадлежит к классу объектов, охарактеризованных определением;
- нахождение логических и содержательных ошибок в приведенных определениях.
3адание 3. Выберите по одному определению из таблицы 2 и выполните логический анализ этих определений, т. е. выделите род, термин и видовые отличия. Охарактеризуйте видовые отличия в каждом из выбранных вами определении.
Осмыслите каждое слово в следующих определениях на основе требований к определениям (см. [93], с. 43):
1. «Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника».
2. «Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым».
3. «Ордината точки ![]() единичной
окружности, полученной при повороте точки
единичной
окружности, полученной при повороте точки ![]() на угол α радиан, называется
синусом угла α».
на угол α радиан, называется
синусом угла α».
4. «Два числа, отличающиеся друг от друга только знаком, называются противоположными числами».
3адание 4. действие подведения под определение объекта состоит из следующих операций: 1) вычленение всех свойств, зафиксированных в определении; 2) установление логической связи между родом и видовыми отличиями; 3) проверка наличия у примера, подводимого под определение объекта, отмеченных свойств и их связей; 4) получение вывода — объект принадлежит к классу объектов, зафиксированных в определении, или нет.
Пример 1. Определение равнобедренного треугольника. Треугольник называется равнобедренным, если у него две стороны равны.
Свойства равнобедренного треугольника: 1) он треугольник; 2) две стороны его равны. Свойства соединены конъюнктивно.
Действие подведения под понятие можно оформить в таблицу 3.
Таблица 3 (кодопозитив)
|
№ п/п |
|
Свойства объекта |
||
|
Треугольник (да «+», нет «-») |
Две стороны равны (да «+», нет «-») |
Вывод: данный объект есть равнобедренный треугольник (да «+», нет «-») |
||
|
1
2
3
4
|
2,5
|
-
+
+
+ |
-
+
+ |
-
-
+
+ |
При соединении видовых отличий конъюнктивно для принадлежности конкретного объекта к классу определенных объектов необходимо соблюдение (наличие у примера) всех свойств одновременно.
Пример 2. Дробь, у которой числитель больше знаменателя или равен ему, называется неправильной.
Свойства неправильной дроби: дробь, числитель больше знаменателя или числитель равен знаменателю. Видовые свойства соединены дизъюнктивно (табл. 4).
Для принадлежности конкретного объекта к классу, заданному в определении, когда видовые отличия соединены дизъюнктивно, необходимо соблюдение (наличие) родового свойства и хотя бы одного из видовых отличий.
Выполните действия подведения под определение объекта для следующих определений: «линейная функция», «симметричные точки», «скрещивающиеся прямые», «убывающая функция», «геометрическая прогрессия». Результаты действий занесите в таблицу 4.
Таблица 4 (кодопозитив)
|
№ п/п |
Пример |
Свойства объекта |
|||
|
Дробь (да «+», нет «-») |
Числитель больше знаменателя (да «+», нет «-») |
Числитель равен знаменателю (да «+», нет «-») |
Вывод: данный объект есть неправильная дробь (да «+», нет «-») |
||
|
1
2
3
4 |
100
|
+
-
+
+ |
-
-
+
- |
-
-
-
+ |
-
-
+
+ |
3адание 5. Установите эквивалентность следующих определений объектов:
1. а) Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
б) Две плоскости называются взаимно перпендикулярными, если в каждой из них через любую точку проходит прямая, перпендикулярная другой плоскости.
2. а) Угол в ![]() называется прямым
углом.
называется прямым
углом.
б) Прямым углом называют половину развернутого угла.
в) Угол называют прямым, если его градусная мера равна
![]() .
.
3. а) Равенство, содержащее неизвестное число, обозначенное буквой, называют уравнением.
б) Равенство, содержащее переменную, называют уравнением.
4. а) Линейной функцией называется функция. которую
можно задать формулой вида ![]() где x —
независимая переменная; k и b — числа.
где x —
независимая переменная; k и b — числа.
б) Линейной функцией называется функция вида ![]() , где k и b — заданные числа.
, где k и b — заданные числа.
3 а д а н и е 6. Найдите ошибки в следующих «определениях» объектов:
1. Диаметром круга называется наибольшая хорда, проходящая через центр.
2. Четырехугольник, у которого противоположные стороны равны, называется параллелограммом.
3. Ромбом называется четырехугольник, у которого противоположные стороны параллельны, а две смежные равны.
3адание 7. Дан конкретный объект, например параллелограмм ABCD. Какие следствия можно вывести из факта, что данный параллелограмм принадлежит к теоретическому (абстрактному) объекту — параллелограмму? Выполнение действия получения следствий из факта принадлежности конкретного объекта теоретическому весьма плодотворно: не тогда, .когда введено только определение объекта, а когда изучены основные его свойства.
Данное действие можно выполнять при заданиях следующего вида:
Дан параллелограмм ABCD (рис. 1). Что из этого следует или что вы знаете об этой фигуре (какими свойствами она обладает)?

Рис. 1
Выполнение данного действия способствует систематизации свойств объекта и тем самым создает более эффективные предпосылки для использования их при поиске решения задач, в условии которых будет этот объект.
Ранее выполненные задания позволяют определить основные этапы раскрытия содержания математического объекта (формирование определения):
Самостоятельная работа
Задание 8. Раскройте основные этапы формирования определений следующих математических объектов: медианы треугольника, функции, арифметического квадратного корня.
Замечание. Ряд математических объектов, особенно на начальных этапах обучения математике (V-VI классы), не имеет в учебниках определений в виде конкретных предложений. Обычно в таких случаях свойства объектов (модуль числа, одночлен и др.) раскрываются на конкретных примерах и затем вводится термин.
Нетрудно видеть, что и в этих случаях ведется такая же работа, как показано выше, но в силу неподготовленности детей к обобщению и сложности структуры определений объектов в этапах работы над определением объекта первый и четвертый этапы не выполняются, а второй выполняется на эмпирическом уровне.
В связи с высказанным замечанием необходимо особо отметить введение арифметических действий сложения и умножения. Определения этих действий в математике вводятся различно в зависимости от принятой трактовки. Но все они сложны и, конечно же, недоступны учащимся. Поэтому в учебниках чаще всего смысл этих действий показывают на конкретных математических задачах, в содержании которых требуется объединить объекты или найти результат изменения или результаты последовательных изменений. Обобщением, в частности, названных действий выступает действие сложения. для введения действия умножения употребляются другие примеры. Здесь важно отметить, что если определяется действие, то главное — показать операции, его реализующие. Вот им в учебниках и придается существенное значение. Такой подход ко всем действиям существует и в курсе алгебры, и в курсе геометрии.
Литература: [93], [31], [41], [124], [52].
Лабораторная работа № 2
Тема. Логико-математический анализ математических утверждений и общие приемы работы с теоремой.
Цель. Раскрыть общий прием выполнения логико-математического анализа конкретных утверждений, организовать самостоятельную работу по анализу теорем школьного курса математики и раскрыть этапы изучения теорем.
Оборудование. Кодопозитивы с записью основных элементов анализа утверждений, их доказательства, схем, показывающих взаимосвязь между видами теорем, и др. (Вместо кодопозитивов можно использовать самодельные таблицы).
Основное содержание
Задание 1. Ответьте на вопросы:
Исходя из педагогических целей в процессе обучения считаем целесообразным принять:
Предложение (утверждение), истинность которого доказывается, называется теоремой.
Логико-математический анализ структуры утверждения предполагает:
а) выделение разъяснительной части, условия и заключения утверждения;
б) установление факта, какое дано утверждение — простое или сложное.
В процессе проведения лабораторной работы выполняется логико-математический анализ следующего утверждения:
Если сумма цифр числа п делится на 3, то само число п делится на 3.
Выделяется условие: «Сумма цифр числа n делится на 3».
Выделяется заключение: «Само число п делится на 3».
Разъяснительная часть: «n — любое натуральное число». Утверждение сформулировано в импликативной форме. Отмечается, что так как в утверждении одно условие и одно заключение, то утверждение простое.
Используя логические символы, утверждение можно записать так:
![]() (сумма цифр числа n делится на 3)
(сумма цифр числа n делится на 3) ![]() (число п делится на 3).
(число п делится на 3).
Результат анализа можно оформить в виде таблицы (табл. 5).
Таблица 5 (кодопозитив)
|
|
|
|
Структура утверждения |
Разъяснительная часть: утверждение рассматривается на множестве натуральных чисел Условие: сумма цифр числа п делится на 3 Заключение: число n делится на 3 |
|
Утверждение простое, так как содержит одно условие и одно заключение. |
|
Задание 2. Выполните логико-математический анализ утверждения
Вертикальные углы равны,
ответив на вопросы:
1) В какой форме сформулировано утверждение)?
2) Сформулируйте утверждение в импликативной форме.
3) Выделите разъяснительную часть.
4) Выделите условие и заключение утверждения.
5) Установите в зависимости от числа условий и заключений, является ли данное утверждение простым или сложным.
Задание 3. Выполните логико-математический анализ теоремы 3.6 [113].
Краткая запись теоремы может быть такой:
![]()
Теорема сформулирована в импликативной форме.
Разъяснительная часть: теорема
рассматривается на множестве любых пар треугольников АВС и![]() .
.
Условие: ![]() .
.
Сколько условий? (Три.)
Какая связь между условиями? (Соединены союзом «и».)
Заключение: ![]() .
.
Сколько заключений? (Одно.)
Так как в теореме три условия, то теорема сложная.
Задание 4. Заполните таблицу (см. табл. 6) логико-математического анализа теоремы 3.5 [113].
Теорема сформулирована в категорической форме.
Таблица 6 (кодопозитив)
|
|
|
|
Структура теоремы |
Разъяснительная часть: . . . . . . . . . . . . . . . . . . . . . Условие: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Заключение: 1) . . . . . . . . . . . 2) . . . . . . . . . . . . . |
|
Теорема ..., так как ... |
|
Примечание. Союз «и» в формулировке теоремы употребляется в соединительном смысле.
3адание 5. Может ли сложная теорема иметь одновременно несколько условий и несколько заключений? Из школьного учебника геометрии приведите пример такой теоремы.
Задание 6. Сформулируйте утверждение, обратное данному. (Надо оставить без изменения разъяснительную часть, а условие и заключение поменять местами.)
Например, для утверждения
![]() (сумма цифр числа n делится на 3)
(сумма цифр числа n делится на 3) ![]() (число n делится на 3)
(число n делится на 3)
обратным будет утверждение
![]() (число n делится
на 3)
(число n делится
на 3) ![]() (сумма цифр числа п делится на 3).
(сумма цифр числа п делится на 3).
Сформулируйте утверждение, обратное следующему:
Вертикальные углы равны.
Будет ли сформулированное утверждение теоремой? Почему?
3адание 7. Как получить утверждение, противоположное данному? (Если оставить без изменения разъяснительную часть, а условие и заключение утверждения заменить их отрицаниями, то получим утверждение, противоположное данному.)
Для утверждения
![]() (сумма цифр числа
n делится на 3)
(сумма цифр числа
n делится на 3) ![]() (число n делится на 3)
(число n делится на 3)
противоположным будет утверждение
![]() (сумма цифр числа
п не делится на 3)
(сумма цифр числа
п не делится на 3) ![]() (число n не делится на 3).
(число n не делится на 3).
Сформулируйте утверждение, противоположное утверждению
Вертикальные углы равны.
Будет ли это утверждение теоремой?
Сформулируйте утверждения, противоположные теоремам 3.5 и 3.6 [113]. Являются ли эти утверждения теоремами?
3адание 8. Какое получим утверждение: обратное противоположному или противоположное обратному, если оставить без изменения разъяснительную часть и поменять местами условие и заключение утверждения, противоположного данному?
Утверждение
![]() (число n не
делится на 3)
(число n не
делится на 3) ![]() (сумма цифр числа п не делится на 3)
(сумма цифр числа п не делится на 3)
будет обратным противоположному или противоположным обратному?
Сформулируйте для утверждения
Вертикальные углы равны
утверждение, обратное противоположному. Является ли сформулированное утверждение теоремой? Почему?
Сформулируйте утверждения, обратные противоположным для теорем 3.5 и 3.6 [113]. Будут ли они теоремами?
3адание 9. На основании рассмотренных примеров сделайте вывод о взаимосвязи между прямым, обратным, противоположным и обратным противоположному утверждениями. Какие из них одновременно являются теоремами?
Общие приемы работы с теоремой. При индуктивном введении теоремы можно условно выделить следующие этапы ее изучения:
- мотивация изучения теоремы и раскрытие ее содержания (усмотрение геометрического факта и формулировка теоремы);
-
 работа
над структурой теоремы;
работа
над структурой теоремы;
- мотивация необходимости доказательства теоремы;
- построение чертежа и краткая запись содержания теоремы;
- поиск доказательства, доказательство и его запись;
- закрепление теоремы;
- применение теоремы.
Для мотивировки необходимости изучения теорем можно предложить такие приемы:
Прием 1. Обобщение наблюдаемых в жизни фактов и явлений и перевод их на математический язык.
Мотивировать необходимость изучения свойства
Две различные прямые либо не пересекаются, либо пересекаются только в одной точке
можно, предложив предварительно учащимся решить дома следующие задачи:
а) На плане местности четыре населенных пункта отмечены точками А, В, С, К. Выясните, пересекутся ли пути из пункта А в пункт С и из пункта К в пункт В (рис. 2, пути считаем прямолинейными). Если пересекутся, то в скольких точках? Рассмотрите различные возможные случаи расположения населенных пунктов. Могут ли эти пути пересечься в двух точках?
В классе учитель выясняет полученные результаты решения задачи: во всех случаях пути движения либо имеют одну общую точку, либо не имеют ни одной. Отметив, что пути движения в данных задачах были отрезками, предлагается подумать над вопросом: изменится ли вывод, если вместо двух отрезков взять две прямые?
Ответы могут быть разными. Если ответы разные, то сразу можно предложить выяснить, могут ли две прямые иметь две общие точки, и тем самым перейти к доказательству теоремы, мотив изучения которой стал очевидным. Если же ответ один, т. е. две различные прямые пересекаются в одной точке, то учитель говорит, что в этой задаче это действительно так. При решении других задач может быть по-другому: ведь мы не можем рассмотреть все конкретные жизненные ситуации и прорешать все задачи! Как быть?
- Надо доказать, причем так, чтобы было истинно для любого случая.
Этот прием можно использовать при изучении многих теорем.
3адание 10. Подберите или составьте задачи, с помощью которых можно мотивировать изучение теорем 1.2, 2.3, 4.4 [113].
Прием 2. Показ необходимости знания той или иной теоремы для решения практических задач.
Для мотивации изучения теоремы
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны
можно использовать следующую задачу:
 Картографам необходимо было нанести на
карту два населенных пункта А и В (рис. 3). Измерить расстояние
между пунктами оказалось невозможно, так как между ними было озеро. Картографы
поступили следующим образом: они выбрали точку С, от которой можно измерить
расстояние и до пункта А, и до пункта В. Измерили эти
расстояния и построили на бумаге отрезки АС и СВ соответствующей
длины (масштаб можно указать по своему усмотрению), а затем продолжили линии за
точку С, отложили отрезки CD и СМ, равные соответственно
отрезкам СВ и СА, и соединили точки D и М отрезком.
Картографам необходимо было нанести на
карту два населенных пункта А и В (рис. 3). Измерить расстояние
между пунктами оказалось невозможно, так как между ними было озеро. Картографы
поступили следующим образом: они выбрали точку С, от которой можно измерить
расстояние и до пункта А, и до пункта В. Измерили эти
расстояния и построили на бумаге отрезки АС и СВ соответствующей
длины (масштаб можно указать по своему усмотрению), а затем продолжили линии за
точку С, отложили отрезки CD и СМ, равные соответственно
отрезкам СВ и СА, и соединили точки D и М отрезком.
Картографы считают, что расстояние DM равно расстоянию АВ (в соответствующем масштабе). Правы ли картографы?
-
По
условию задачи известно, что АС=СМ, BC=CD и, кроме того, ![]() как вертикальные углы.
как вертикальные углы.
- Надо установить, что DM =АВ.
- Откуда может следовать равенство этих отрезков?
- Равенство отрезков DM и АВ может следовать из равенства треугольников АСВ и DCM.
- Но в равных треугольниках соответственно равны все шесть элементов (по три угла и по три стороны), а здесь мы имеем только две стороны и угол между ними одного треугольника, соответственно равные двум сторонам и углу между ними другого треугольника. Как быть?
- Следует доказать, что если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Мотив изучения и необходимость доказательства теоремы показаны.
Задание 11. Подберите подходящую практическую задачу для мотивации изучения теоремы.
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Прием 3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем.
Например, перед доказательством теоремы 3.3 [113] учащимся предлагается решить задачу:
В равнобедренном треугольнике АВС (АВ=BС) вершина угла В соединена с серединой К стороны АС отрезком. Докажите, что треугольники АВК и СВК равны. Достаточно ли этих данных, чтобы установить равенство названных треугольников?
Так как третьего признака равенства треугольников по трем сторонам (теорема 3.6) у учащихся пока нет, то данную задачу они решить не могут. Созданная проблемная ситуация позволяет сразу мотивировать необходимость изучения сразу трех теорем 3.3, 3.5, 3.6 [113].
Задание 12. Покажите, как, осуществляя поиск решения сформулированной выше задачи, можно мотивировать изучение теорем 3.3, 3.5, 3.6. (Задание выполняется группами по 3-5 человек.)
Прием 4. Показ, как решалась данная проблема в истории науки.
Задание 13. Подберите пример. где бы использовался этот прием мотивации изучения теорем.
Очевидно, что перечисленные выше приемы для мотивации изучения теорем служат одновременно и раскрытию содержания теоремы. Из других приемов раскрытия содержания теорем можно назвать:
- наблюдение наглядного материала, в том числе подвижных моделей или ряда чертежей;
- выполнение построений;
- решение задач на вычисление и доказательство;
- выполнение лабораторных или практических работ;
- решение задач на отыскание некоторых зависимостей.
Приводятся примеры.
Пример 1. Чтобы раскрыть содержание теоремы 2.4,
учащимся предлагается в тетрадях (чтобы потом можно было использовать чертеж и
для дальнейшей работы) начертить полупрямую а, отложить от
полупрямой а в одну полуплоскость ![]() , причем
, причем ![]() . На доске эту работу можно предложить
выполнить двум-трем ученикам. После построения чертежей ставится вопрос: как
проходит сторона b по отношению к сторонам угла (ас)?
. На доске эту работу можно предложить
выполнить двум-трем ученикам. После построения чертежей ставится вопрос: как
проходит сторона b по отношению к сторонам угла (ас)?
Несмотря на то что все брали разные углы (но у всех ![]() , оказалось, что сторона b проходит
между сторонами угла (ас). Отмечается, что результаты этих
наблюдений можно обобщить и сформулировать теорему. В случае надобности учитель
корректирует формулировку теоремы.
, оказалось, что сторона b проходит
между сторонами угла (ас). Отмечается, что результаты этих
наблюдений можно обобщить и сформулировать теорему. В случае надобности учитель
корректирует формулировку теоремы.
Пример 2. Для раскрытия содержания теоремы Фалеса (теорема 6.6) можно использовать следующий прием: начертить в тетрадях угол (произвольный) (на доске это делает учитель); отложить на одной стороне угла последовательно несколько равных отрезков; через концы отрезков провести параллельные прямые до пересечения со второй стороной угла; измерить отрезки, получившиеся на второй стороне угла, и сравнить их между собой. После этой работы высказывается предположение (формулируется теорема), которое затем доказывается.
Пример 3. Раскрыть содержание теоремы 6.4 можно, решив с учащимися устно несколько задач вида «Вычислите диагонали прямоугольника АВСК, если его стороны равны: а) 3 и 4 см; б) 6 и 8 дм; в) 12 и 9 м». Какой вывод можно сделать из решения этих задач?
Задание 14. Покажите возможные приемы раскрытия содержания теорем 4.4, 4.5, 6.1.
Образец записи доказательства теоремы на примере теоремы 3.5 (табл. 7):
Таблица 7
Дано:
![]() — равнобедренный,
— равнобедренный,
BK — медиана, проведенная к основанию.
Доказать:
1. BK — биссектриса,
2. BK — высота.
Доказательство
Можно составить структурную схему доказательства. Приведем такую схему для случая (1) (кодопозитив):
Отдельно схему для случая (2) можно изобразить так (кодопозитив):
Схема доказательства всей теоремы может быть представлена и так:
Чтобы теорема была усвоена, необходима работа с ней и после ее доказательства. Этому способствуют задания следующих видов:
При этом предлагаются задачи на применение только что изученной теоремы: задачи на распознавание фигур или взаимного положения элементов фигур на чертежах, к которым можно применить теорему, причем решение задачи в этом случае до конца можно и не доводить; задачи, для решения которых используется изученная теорема наряду с другими, ранее изученными.
Само собой разумеется, что эта работа проводится не только на одном-двух уроках, когда изучается та или иная теорема, а по мере возможности проводится и при изучении других вопросов.
Проследим все этапы работы над теоремой на примере теоремы:
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
I этап. Один из приемов мотивации изучения этой теоремы — знание теоремы для решения задач.
Можно использовать другой. прием, показав конструкцию строительной фермы (рис. 4), где АС=СВ, AD=DB, DM=MB; простейшую конструкцию стропил (рис. 5) АВ=ВС и АК=КС, т.е. наблюдение жизненных фактов.
С целью мотивации изучения этой теоремы можно использовать решение практической задачи.
Чтобы провесить с помощью веревки перпендикуляр к данной прямой MN из данной на ней точки, поступают так: откладывают от этой точки О равные расстояния ОВ и ОА; прикрепляют к колышкам А и В концы веревки и, взяв веревку за середину С, натягивают ее; провешенная прямая СО и будет искомым перпендикуляром. Почему? (Рис. 6.)
Можно использовать решение учебно-практической задачи:
Чтобы разделить угол Р пополам с помощью только масштабной линейки, поступают так: 1) откладывают на сторонах угла Р (рис. 7) равные отрезки РМ и РК; 2) соединяют точки М и К отрезком; 3) делят отрезок МК пополам, получают точку В; 4) проводят луч РВ. РВ — искомая биссектриса, разделившая угол пополам. Почему?
II этап. Чтобы учащиеся «открыли» сами содержание теоремы и сформулировали ее, проводится такая практическая работа. Перед уроком дается на дом задание: начертить три равнобедренных треугольника (остроугольный разносторонний, прямоугольный и тупоугольный) и в этих треугольниках построить медианы и высоты к боковым сторонам (с помощью масштабной линейки и угольника), биссектрисы углов при основании (с помощью транспортира). А на уроке предлагается по вариантам выполнить другую практическую работу: начертить в тетрадях равнобедренный треугольник
I вариант
Остроугольный
II вариант
Прямоугольный
III вариант
Тупоугольный
и построить медиану и высоту к основанию и биссектрису угла при вершине, противолежащей основанию. Трое учащихся (по одному от каждого варианта) выполняют эту работу на доске. Учитель тем временем может построить разносторонний треугольник и провести в нем медианы, высоты и биссектрисы (этот рисунок можно заготовить заранее).
После выполнения практической работы обсуждаются ее результаты. У учащихся в каждом из данных случаев медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой.
Ставятся вопросы: обладает ли этим свойством медиана, проведенная из вершин двух других углов равнобедренного треугольника к противолежащей стороне) Нет. Это видно из рисунков, выполненных в домашней практической работе.
Обладают ли этим свойством медианы, проведенные в разностороннем треугольнике? Нет. Учитель демонстрирует свой рисунок.
Итак, практическим путем установлен новый факт. Какой? Учащиеся формулируют теорему. Если есть необходимость, учитель уточняет их ответы.
III этап. Мотивируется необходимость доказательства теоремы.
Перед учащимися ставится вопрос: во всех ли равнобедренных треугольниках медиана, проведенная к основанию, является биссектрисой и высотой?
— Неизвестно. В тех, которые рассматривались, да. А в других — неизвестно. Как быть?
Делается вывод о том, что необходимо доказать справедливость теоремы для любого равнобедренного треугольника.
IV этап. Проводится работа над структурой теоремы: выделяется условие, заключение, еще раз уточняется, что теорема сформулирована для равнобедренного треугольника. На доске и в тетрадях выполняется чертеж, записывается, что дано и что требуется доказать (см. табл. 7).
V этап. Поиск доказательства осуществляется движением от заключения к условию, т.е. аналитически (см. с. 194-200). Записывается доказательство (см. табл. 7).
Работа по закреплению теоремы
VI этап. Усвоение формулировки теоремы.
1) Верно ли сформулирована теорема: «Медиана, проведенная к основанию, является биссектрисой и высотой»? Почему?
2) Вставьте пропущенные слова: «В ... треугольнике медиана, проведенная ..., является ... и ... ».
Текст проецируется через кодоскоп.
3) Сформулируйте теорему со словами: «Если ... , то ... ».
VII этап. Усвоение доказательства теоремы.
VIII этап. Решение задач на применение теоремы.
1) Точка M принадлежит высоте равнобедренного треугольника, проведенной к основанию. Принадлежит ли эта точка: а) биссектрисе угла при вершине? б) медиане, проведенной к основанию? Почему?
2) Точка Р принадлежит биссектрисе угла треугольника. Принадлежит ли эта точка высоте треугольника? Почему?
3) Можно ли с помощью только масштабной линейки построить биссектрису угла при вершине равнобедренного треугольника? Высоту? Дайте обоснование ответа.
4) Длина медианы равнобедренного треугольника, проведенной к основанию, равна 10 см. Чему равны длины биссектрисы и высоты, проведенных из той же вершины?
5) Докажите, что в равностороннем треугольнике биссектриса каждого из углов является медианой и высотой, проведенными из вершины угла к противоположной стороне. Будут ли равны все биссектрисы, медианы и высоты между собой?
Предлагается решить более сложные задачи, например № 23, 27, 29 и др. [113].
Самостоятельная работа
1. Выполните логико-математический анализ теоремы: «Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны».
2. Для этой теоремы сформулируйте утверждения: обратное, противоположное и противоположное обратному.
3. Выделите основные этапы работы с данной теоремой в классе.
Литература: [125], [93], [32], [52], [l6], [17], [18], [44], [45], [46].
Лабораторная работа № 3
Тема. Логико-математический анализ алгоритмов и правил школьного курса математики. Методика работы в школе с алгоритмами и правилами.
Цель. Познакомить с особенностями логико-математического анализа алгоритма (правила) и с содержанием основных этапов работы при его формировании; в ходе коллективной работы выполнить логико-математический анализ алгоритма сложения десятичных дробей и разобрать содержание основных этапов работы с ним.
Оборудование. 1. Кодопозитивы с изображением схем алгоритмов сложения и умножения десятичных дробей.
2. Дидактические материалы с наборами упражнений, которые могут быть использованы на отдельных этапах работы по формированию алгоритма сложения десятичных дробей.
Основное содержание
Элементами теоретических знаний, с которыми школьники встречаются при изучении математики наряду с определениями понятий, аксиомами и теоремами, являются алгоритмы.
Понятие «алгоритм» является основным, неопределяемым. Сущность его на содержательно-интуитивном уровне может быть описана следующим образом: алгоритм — понятное предписание, указывающее, какие операции и в какой последовательности необходимо выполнить с данными, чтобы решить любую задачу данного типа.
Известно, что алгоритм обладает свойствами массовости, элементарности и дискретности шагов, детерминированности и результативности.
Свойство массовости предполагает, что с помощью данного алгоритма могут быть решены все задачи определенного типа.
Свойство дискретности и элементарности шагов состоит в том , что при построении алгоритма выделяются строго дискретные (отдельные и законченные) шаги (операции), каждый из которых в состоянии выполнить исполнитель (в этом смысле каждый шаг считается элементарным). В записи алгоритма свойство дискретности выражается в выделении отдельных пунктов (указаний) при словесной форме, или блоков на языке алгоритмов.
Свойство детерминированности подразумевает то, что решение задач по данному алгоритму является процессом строго («жестко») направленным: он однозначно определяет первый шаг и каждый следующий.
Свойство результативности полагает, что точное выполнение указаний алгоритма при решении любой задачи из данного класса однотипных задач всегда (в конечное число шагов) должно приводить к определенному результату. Заметим, что этим результатом может быть установление факта, что задача решения не имеет.
Перечисленные свойства являются характеристическими свойствами понятия «алгоритм».
Всякий алгоритм описывает общий метод решения класса однотипных задач, т.е. алгоритм является формой выражения этого метода.
Для описания общего метода решения класса однотипных задач в школе также часто используются правила.
Правило представляет собой «свернутый» алгоритм. Отдельные шаги его являются блоками (системами операций в «сжатом» виде); некоторые операции, необходимые на начальном этапе формирования метода, вообще не содержатся в формулировке правила.
Правила в учебниках выражаются формулами и формулировками на естественном языке. Использование правил имеет ту же цель, что и алгоритмов: формирование общих методов решения класса однотипных задач.
Всякий алгоритм можно назвать правилом. но не всякое правило можно назвать алгоритмом: в формулировке правила часто четко не выделяются все шаги — оно не обладает в этом случае свойством детерминированности.
Для того чтобы правильно организовывать работу учащихся по овладению алгоритмами школьного курса математики, учителю необходимо овладеть умением выполнять логико-математический анализ алгоритмов (правил).
Логический анализ алгоритмов (правил) предполагает: а) проверку наличия у данного правила характеристических свойств алгоритма; б) выделение последовательности операций и логических условий в данном правиле; в) установление связи алгоритма (правила) с другими знаниями.
Математический анализ алгоритмов (правил) состоит в установлении математической основы данного правила, т.е. тех базовых математических положений, которые позволяют построить именно такое правило (они обычно называются обосновывающими знаниями).
Покажем логико-математический анализ правила на примере правила сложения десятичных дробей.
Приведем формулировку правила, изучающегося в V классе:
Чтобы сложить две десятичные дроби, надо: 1) уравнять число знаков после запятой в слагаемых; 2) записать слагаемые друг под другом так, чтобы запятая оказалась под запятой; 3) сложить получившиеся числа, как складывают натуральные числа; 4) поставить в полученной сумме запятую под запятыми в слагаемых.
Прежде всего обратим внимание на выполнение характеристических свойств алгоритма.
В словесной формулировке правила выделены дискретные шаги, каждый из которых представляет собой операцию, ранее сформированную у учащихся (например, сложение натуральных чисел или приписывание нулей в дробной части десятичной дроби), и в этом смысле элементарную или действительно простейшую, элементарную операцию (подписывание слагаемых друг под другом, постановка запятой в результате). Поэтому приведенное правило обладает свойствами дискретности и элементарности шагов.
В словесной формулировке также строго указана последовательность шагов (все шаги занумерованы). Это говорит о том, что данное правило обладает свойством детерминированности.
Это правило обладает свойством массовости. Применяя его, можно сложить любые две десятичные дроби. Нужно только иметь в виду, что первая операция, выделенная в правиле, выполняется только тогда, когда число знаков в дробных частях слагаемых различно.
Наконец, применяя данное правило, всегда найдем сумму любых двух десятичных дробей. Это значит, что данное правило обладает свойством результативности.
Таким образом, это правило сложения двух десятичных дробей обладает всеми характеристическими свойствами алгоритма, поэтому его можно назвать алгоритмом.
В алгоритме уже выделены операции и указана их последовательность. Однако, учитывая замечание, сделанное при рассмотрении свойства массовости, целесообразно выделить логическое условие, определяющее число знаков в дробных частях слагаемых.
Задание 1. Запишите алгоритм
сложения двух десятичных дробей с помощью схемы (рис. 9).
Анализ полученной схемы позволяет установить связи данного алгоритма с другими знаниями: основным свойством дроби для случая десятичной дроби (получение равных десятичных дробей при приписывании или отбрасывании нулей в конце дробной части десятичной дроби), алгоритмом сложения натуральных чисел.
Кстати, вспоминая алгоритм сложения натуральных чисел, необходимо выяснить, что в его основе лежит поразрядный принцип сложения этих чисел, который присущ и сложению десятичных дробей.
Для того чтобы выполнить математический анализ алгоритма, необходимо за операциями алгоритма увидеть их математическую основу, или, другими словами, ответить на вопрос, на основании каких математических знаний можно выполнять ту или иную операцию, входящую в алгоритм.
Операции алгоритма сложения двух десятичных дробей формализуют поразрядный принцип сложения этих чисел. Использование этого принципа (как и в случае натуральных чисел) связано с особенностями нумерации десятичных дробей (позиционный принцип записи десятичных дробей) и с возможностью применения законов сложения для сложения единиц одного разряда.
Например, при сложении чисел 2,35 и 0,21 можно представить каждое из слагаемых в виде суммы разрядных слагаемых.
2,35=2+0,3+0,05;
0,21=0,2+0,01.
Затем, применив переместительный и сочетательный законы сложения, сложить единицы одного разряда, т. е.
(2+0,3+0,05)+(0,2+0,01)=2+(0,3+0,2)+(0,05+0,01)=2+0,5+0,06.
И наконец, результат, записанный в виде суммы разрядных слагаемых, представить в виде десятичной дроби 2,56.
Таким образом, обосновывающими знаниями для рассматриваемого алгоритма являются правила нумерации десятичных дробей и законы сложения, которые дают возможность выполнять сложение поразрядно.
Логико-математический анализ алгоритма позволяет правильно осуществить отбор материала для работы с учащимися по овладению алгоритмом.
Работа с учащимися по овладению алгоритмом обычно включает три основных этапа: 1) введение алгоритма; 2) усвоение алгоритма; 3) применение алгоритма.
Охарактеризуем цель каждого из выделенных этапов:
цель первого этапа — актуализация знаний, необходимых для введения и обоснования алгоритма, а также формулирование алгоритма;
цель второго этапа — отработка операций, входящих в алгоритм, и усвоение их последовательности;
цель третьего этапа — отработка алгоритма в знакомых (при варьировании исходных данных) и незнакомых ситуациях.
Основным средством, используемым на различных этапах формирования алгоритма, является система упражнений. Содержание ее определяется на основании логико-математического анализа конкретного алгоритма.
Можно выделить и преобладающие формы работы с учащимися на разных этапах формирования алгоритма. Так, на первом этапе это устная работа на повторение. На втором этапе — письменная коллективная работа с широким использованием комментирования выполняемых действий. На третьем этапе — самостоятельная работа.
Задание 2. На основании выполненного логико-математического анализа алгоритма сложения десятичных дробей проанализируйте содержание упражнений, отобранных для каждого этапа формирования алгоритма. Соотнесите отбор упражнений с целью каждого этапа.
Упражнения для первого этапа
1) (Устно.) Выполните сложение дробей и поясните его выполнение:
|
а) |
в) |
д) |
|
б) |
г) |
е) |
2) Запишите следующие десятичные дроби в виде обыкновенных:
0,1; 0,7; 0,09; 0,61; 0,057.
3) Найдите сумму чисел: а)![]() ; б)
; б)![]() .
.
4) Представьте следующие числа в виде суммы разрядных слагаемых: 457; 4,57; 42; 0,42.
5) Сложите числа, представив их в виде суммы разрядных слагаемых и применив переместительный и сочетательный законы сложения: а) 457+42; б) 4,57+0,42.
6) Выполните сложение, называя каждый раз, единицы каких разрядов складываете:
Упражнения для второго этапа
1. Найдите сумму:
Объясните, почему так записаны слагаемые.
2. Какую цифру второго слагаемого нужно записать под последней цифрой первого слагаемого при сложении «в столбик»?
Выполните сложение.
3. Сравните записи сложения натуральных чисел и десятичных дробей «в столбик». Чем они отличаются друг от друга?
4. Выполните сложение:
1) 0,56+3,24
2) 0,789+0,311
3) 137,764+42,236
Образец записи:
Упражнения для третьего этапа
1. (Устно.) 0,47+0,01; 1,6+4,3; 3,7+2,3; 0+0,78;
0,47+0,1; 3,25+3,5; 7,5+75; 4,69+1.
2. Найдите сумму и проверьте, применив переместительный закон сложения:
|
1) 86,97+32,35 2) 121,4+39,6 |
3) 974,511+25,489 4) 38,5+0,86 |
5) 695,7+0,6957 6) 7561+786,9 |
3. В левом столбце записаны выражения, в правом — их значения. Около каждого числа правого столбца поставьте номер выражения, для которого оно является значением:
|
1) 176,4+37,59 2) 24,569+185,46 3) 13,473+0,427 4) 0,487+0,523 5) 890,08+0,92 |
891 13,9 213,99 210,029 1,01 |
4. Найдите сумму чисел:
1) 58,284+1,84+107,907
2) 0,0347+59,6+789,005+0,489
5. Выполните сложение наиболее удобным способом::
1) 307,1+100,1+0,99
2) 27,34+5,407+2,66+4,983
6. Сложите числа:
1)![]() 2)
2)![]() .
.
Алгоритмы и правила имеют общее функциональное назначение — формирование общих методов решения класса однотипных задач. Однако их методическое назначение может быть различно. Алгоритм целесообразно использовать на первоначальных этапах формирования действия, так как он дает подробное описание последовательности операций. Правило удобно применять тогда, когда в основном умение выполнять действие уже сформировано и ученику не нужно подробное описание операций.
В школьных учебниках математики большинство правил сформулировано в лаконичной и «сжатой» форме. Для обучения учащихся выполнению соответствующего правила действия учителю часто необходимо записать его в виде алгоритма.
Покажем, как это можно сделать, на при мере правила умножения двух десятичных дробей ([39], с. 231).
В учебнике есть дополнительное замечание о том, что иногда в произведении может получиться меньше цифр, чем нужно отделить запятой, - в этом случае слева к произведению приписывают нули.
Учитывая это замечание, сформулируем в словесной форме алгоритм умножения двух десятичных дробей.
Чтобы умножить одну десятичную дробь на другую, надо:
1) подписать их друг под другом так, как при умножении натуральных чисел (не обращая внимания на запятые);
2) выполнить умножение чисел как натуральных, не обращая внимания на запятые;
3) подсчитать общее число цифр после запятой в обоих множителях вместе (s);
4) сравнить это число с числом цифр, полученных в произведении (n);
5) если число цифр в произведении больше числа цифр, стоящих после запятой в обоих множителях вместе (s<n), то в произведении справа отделить столько цифр запятой, сколько их после запятой в обоих множителях вместе;
если нет, то приписать к произведению слева один или несколько (s-n)+1 нулей и отделить столько цифр в произведении справа, сколько их после запятой в обоих множителях вместе (т.е. s).
Этот же алгоритм можно записать в виде схемы (рис. 10).
Самостоятельная работа
1. Выполните полный логико-математический анализ построенного алгоритма умножения десятичных дробей.
2. Подберите упражнения для работы с учащимися на каждом из трех этапов формирования алгоритма умножения десятичных дробей.
Задания для домашней работы
Выполните логико-математический анализ:
алгоритма сравнения обыкновенных дробей с разными знаменателями [40], [23];
алгоритма сложения (вычитания) обыкновенных дробей с разными знаменателями [40], [23];
правила деления десятичной дроби на натуральное число [39], [24];
правила умножения одночлена на многочлен [6], [2].
Примечание. При выполнении логико-математического анализа алгоритма (правила) необходимо записать его в виде схемы, установить связи правила с другими знаниями, перечислить обосновывающие знания.
Литература: [93], [115], [69], [3], [7].
Лабораторная работа № 4
Тема. Задачи как средство обучения математике.
Цель. Познакомить с особенностями систем задач, направленных на формирование элементов знаний по математике (математических понятий, их определений, теорем и их доказательств, правил); проанализировать в учебниках математики системы задач, направленных на усвоение учащимися понятии «правильная дробь» и «неправильная дробь», теоремы о сумме углов треугольника; задачи контрольных работ по темам: «Обыкновенные дроби» (V кл.), «Сумма углов треугольника» (VII кл.).
Оборудование. 1. [39], [47].
2. Дидактические материалы: примерные контрольные работы для V — VI классов — контрольная работа № 8 (см.: Математика в шк. - 1984. - № 6); примерные контрольные работы по геометрии в VII классе — контрольная работа № 4 (см.: Математика в шк. - 1985. - № 4); самостоятельные работы по геометрии в VII классе - (С-11) (см.: Математика в шк. - 1982. - № 6).
Основное содержание
Основным средством, которое используется при обучении математике для формирования знаний, умений и навыков учащихся, являются задачи. Посредством решения задач мы не только реализуем образовательную цель обучения математике, но и развивающую и воспитательную цели.
По своему функциональному назначению в процессе обучения задачи как средство обучения могут быть непосредственно направлены на формирование знаний, умений и навыков учащихся (обучающие задачи) или на осуществление контроля со стороны учителя или учащихся уровня сформированности знаний, умений и навыков (контролирующие задачи).
Обучающие задачи прежде всего связаны с формированием элементов теоретических знаний и связанных с ними умений. К теоретическим знаниям, которые формируются при изучении математики, можно отнести понятия и их определения, теоремы и их доказательства, правила (алгоритмы).
Нужно отметить, что большую нагрузку в формировании практических математических умений и навыков несут задачи, направленные на формирование правил (алгоритмов). В ходе решения этих задач формируются вычислительные умения и навыки, навыки тождественных преобразований алгебраических и трансцендентных выражений, умения и навыки решения уравнений и неравенств определенных типов и др. Поскольку формирование умений и особенно навыков требует неоднократного повторения определенной последовательности операций, другими словами, упражнений по выполнению того или иного действия, то задачи, связанные с формированием умений и навыков учащихся, обычно называют упражнениями.
Однако не только упражнения направлены на формирование умений и навыков учащихся. В ходе решения задач, направленных на усвоение понятий и теорем, формируются, например, умения выделять существенные признаки понятий, анализировать структуру определений и формулировок теорем, использовать существенные признаки и свойства понятий, а также факты, полученные в ходе доказательства теорем, в различных ситуациях.
Для формирования выделенных элементов теоретических знаний и овладения учащимися соответствующими им видами деятельности недостаточно одной задачи. Речь должна идти о системе задач, обеспечивающей всеобъемлющее усвоение учебного материала.
Перечислим общие и специфические особенности систем обучающих задач, направленных на формирование элементов теоретических знаний.
Общим для систем задач, направленных на усвоение учащимися понятий, теорем и правил, является наличие в них задач, подготавливающих введение соответствующего элемента теоретических знаний, связанных с его анализом (построением), с его применением. Среди подготовительных задач обычно выделяются задачи на мотивацию изучения понятий, теорем, правил и задачи на актуализацию знаний, умений и навыков, необходимых при работе с новым учебным материалом.
Особенности системы задач на усвоение понятия и его определения:
1. Наличие задач, связанных с показом практической значимости нового понятия или с его значимостью для дальнейшего продвижения в изучении математики.
2. Наличие задач на актуализацию знаний и умений, необходимых при формировании данного понятия.
3. Наличие задач на выделение существенных признаков понятия.
4. Наличие задач на распознавание формируемого понятия.
5. Наличие задач на усвоение текста определения понятия.
6. Наличие задач на использование символики, связанной с понятием.
7. Наличие задач на установление свойств понятия.
8. Наличие задач на применение понятия.
Известно, что не всегда работа с понятием предполагает формулирование его определения (особенно это относится к понятиям, рассматриваемым в V-VI классах). В этом случае в системе задач будут отсутствовать задачи на усвоение текста определения.
Приведенная система задач обеспечивает формирование двух учебных действий: подведение объекта под понятие (см. 3, 4); выведение следствий из факта принадлежности объекта данному понятию (см. 7, 8).
Особенности системы задач на усвоение теоремы и ее доказательства:
1. Наличие задач на раскрытие необходимости знания математического факта, сформулированного в теореме.
2. Наличие задач на актуализацию математических фактов, используемых при доказательстве данной теоремы, или фактов, для которых данная теорема является обобщением, а также на актуализацию способов доказательства, аналогичных используемым в данной теореме (например, способа от противного).
3. Наличие задач на вычисление и доказательство или на построение, которые приводят учащихся к осознанию факта, сформулированного в теореме.
4. Наличие задач на усвоение формулировки теоремы.
5. Наличие задач на усвоение отдельных этапов доказательства теоремы.
6. Наличие задач, в ходе решения которых повторяется ход доказательства теоремы (например, при измененном чертеже).
7. Наличие задач на отыскание другого способа доказательства факта, сформулированного в теореме.
8. Наличие задач на применение факта, сформулированного в теореме, для получения новых математических фактов, установления количественных соотношений между объектами или получения способов построения объектов.
Задачи, приведенные в предлагаемой системе под цифрой 1, могут быть использованы для создания проблемных ситуаций. Как и в случае с системой упражнений, направленной на формирование понятий, приведенная система дает возможность для формирования учебных действий, связанных с усвоением теорем и их доказательств.
Особенности системы задач на усвоение правил (алгоритмов):
1. Наличие задач на обоснование необходимости рассмотрения правила.
2. Наличие задач на актуализацию знаний, необходимых для обоснования правил, и умений, необходимых для выполнения правил.
3. Наличие задач на выполнение отдельных операций, входящих в алгоритм (правило).
4. Наличие задач на применение правил в различных ситуациях (знакомых и незнакомых).
Пример такой системы задач (упражнений) приведен в лабораторной работе, посвященной логико-математическому анализу алгоритмов и правил.
Отметим, что описанные системы задач обладают некоторой избыточностью. Наличие или отсутствие в них задач некоторых видов зависит и от места изучения соответствующего учебного материала, и от содержания рассматриваемого материала, и от методической концепции его изучения.
Контролирующие задачи чаще всего включаются в самостоятельные (проверочные) и контрольные работы. По содержанию эти задачи предполагают применение полученных теоретических знаний.
Задачи, которые включаются в самостоятельные работы, обычно предполагают применение знаний учащихся в знакомых ситуациях, т. е. в таких, с которыми ученики встречались на предшествующих уроках. Отличительной чертой задач, включаемых в самостоятельные работы, является то, что они охватывают сравнительно небольшой отрезок учебного материала.
Задачи, включаемые в контрольные работы, обычно охватывают более значительный, законченный отрезок учебного материала (материал параграфа учебника или целой главы). Они удовлетворяют следующим требованиям:
- направлены на проверку усвоения основного (ядерного) материала;
- большая часть рассчитана на применение основных понятий, математических фактов, сформулированных в виде теорем и следствий из них, правил в знакомых учащимся ситуациях;
- наличие задач на применение знаний в незнакомой ситуации, требующей самостоятельного отыскания пути решения.
Самостоятельная работа
1. Проанализируйте систему задач для формирования понятий «правильная дробь» и «неправильная дробь» [39], проверив наличие в ней видов задач, выделенных в системе для формирования понятий и их определений.
Примечание. Для выполнения этого задания можно предварительно: 1) выполнить логико-математический анализ понятий «правильная дробь» и «неправильная дробь», проанализировать логическую структуру определений этих понятий; 2) устно решить задачи, помещенные после п. 37.
2. Проанализируйте задачи № 12-24 ([113]) с точки зрения удовлетворения требованиям, предъявляемым к системе задач для усвоения теорем и их доказательств. Дополнительно рассмотрите вопросы для повторения 8 и 9 ([113]).
Примечание. Предварительно необходимо проанализировать формулировку и доказательство теоремы о сумме углов треугольника и решить указанные задачи.
В результате проведенного анализа ответьте на следующие вопросы:
1) Является ли соответствующая система задач полной (в смысле наличия всех видов задач, перечисленных в общих схемах)?
2) Почему некоторые виды задач в анализируемых системах отсутствуют?
3) Какими задачами рассматриваемые системы целесообразно дополнить?
3. Решите и проанализируйте задачи самостоятельной работы (С-11) по теме «Сумма углов треугольника» (см.: Математика в шк. - 1982. - № 6. - С. 40; варианты 1-4).
В результате анализа ответьте на вопросы:
1) Какие понятия используются в задачах самостоятельной работы?
2) Какие факты должны знать учащиеся для решения этих задач?
3) В чем различие между первой и второй задачами самостоятельной работы?
4) Есть ли среди задач, помещенных в учебнике, задачи, аналогичные включенным в самостоятельную работу?
5) Одинаковы ли по сложности задачи, приведенные в первом, втором, третьем и четвертом вариантах самостоятельной работы?
4. Выполните анализ контрольной работы № 8 к пп. 33-37 учебника [39] (см.: Математика в шк. - 1984. - № 6. - С. 31). Для этого
установите, какие знания и умения учащихся проверяются в каждой из пяти задач контрольной работы;
выясните, охватывают ли задачи контрольной работы весь основной теоретический материал и основные способы деятельности, которые формируются при изучении указанных пунктов учебника;
определите, есть ли среди задач, помещенных в учебнике, аналогичные тем, которые включены в контрольную работу (укажите номера этих задач);
установите, одинаков ли уровень сложности всех задач контрольной работы.
Примечание. Для выполнения четвертого задания необходимо предварительно познакомиться с содержанием теоретического и задачного материала пп. 33-37 учебника [39].
Задания для домашней работы
1. Составьте систему задач для формирования понятия кратного некоторого числа (см. [39], п. 22), используя задачи учебника и дополнительные материалы.
2. Составьте систему задач для формирования понятия делителя некоторого числа (см. [39], п. 22), используя задачи учебника и дополнительные материалы.
3. Составьте систему задач для формирования понятия многочлена (см. [6]), используя задачи учебника и дополнительные материалы.
4. Составьте систему задач для формирования понятия выпуклого многоугольника (см. [113]), используя вопросы для повторения, задачи учебника и дополнительные материалы.
Литература: [93], с. 148-167; [10], [81], [79], [86], [87], [105].
Лабораторная работа № 5
Тема. Методика работы с сюжетной задачей в школе.
Цель. Обобщить знания по теории задач, установить основные этапы деятельности по решению задач, выяснить общие приемы работы над задачей как целью изучения, рассмотреть методику работы над сюжетной задачей в курсе математики V - VI классов.
Оборудование. 1. Наборы задач. 2. Кодопозитивы с примерами форм краткой записи условия и решения задач. 3. Набор задач для самостоятельной работы.
Обучение математике — обучение решению задач. В частности, на практикуме по решению задач рассмотрены некоторые вопросы теории задач. Актуализация знаний по теории задач осуществляется при обсуждении вопросов.
3адание 1. Ответьте на вопросы:
1) Какова структура любой задачи?
2) В чем суть алгоритмического метода решения задачи? Приведите примеры алгоритмов решения задач.
3) Какова суть эвристического метода решения задач и какие приемы поиска решения задач при этом используются?
4) Охарактеризуйте общие приемы поиска решения задач в пособии [93] (с. 167-175).
5) Перечислите этапы в деятельности по решению задач.
После обсуждения указанных вопросов приходим к выводам, которые кратко могут быть зафиксированы так:
Различные типы задач требуют использования разных методов и приемов решения. Все методы решения можно разделить на две группы: алгоритмические и эвристические.
При решении сюжетных задач, особенно на этапе поиска решения задач определенного класса или поиска алгоритмического предписания для решения задач нового класса, используется эвристический метод.
Эвристика (греч. «отыскание») - специальные методы, используемые в процессе отыскания нового;
- наука, изучающая продукт теоретического мышления;
- восходящий к Сократу (470-399 до н.э.) метод обучения.
При эвристическом методе решения чаще всего используются следующие приемы поиска решения задачи: серии вспомогательных задач, целенаправленных проб, моделирования (составление схем алгоритмов, графов разного уровня, уравнений, систем уравнений и др.).
В деятельности по решению задач чаще всего выделяют четыре этапа:
Задание 2. Ответьте на вопросы:
1. В чем дидактическая ценность сюжетных задач, решаемых в курсе математики V-VI классов?
2. Какие способы решения этих задач рассматриваются в V-VI классах?
Сюжетной задачей называют такую задачу, в которой данные и связь между ними включены в фабулу. Содержание сюжетной задачи чаще всего представляет собой некоторую ситуацию, более или менее близкую к жизни. Эти задачи важны главным образом для усвоения учащимися математических отношений, для овладения эффективным методом познания — моделированием, для развития способностей и интереса учащихся к математике.
Решение задач в V-VI классах осуществляется в основном тремя способами:
- арифметическим, при котором все логические операции при решении задачи проводятся над конкретными числами и основой рассуждения является знание смысла арифметических действий;
- алгебраическим, при котором составляется уравнение (система уравнений), решение которого основано на свойствах уравнений;
- комбинированным, который включает как арифметический, так и алгебраический способы решения.
Работа над любой задачей начинается с разбора ситуации, указанной в задаче, повторения текста задачи с числовыми данными. Здесь может быть использован прием беседы по условию задачи, результатом которой будет краткая запись. Краткая запись условия задачи играет существенную роль на этапе принятия задачи. Форма записи условия задачи должна быть компактной: в ней должно быть отражено только то, что необходимо для решения.
Рассмотрим пример.
Задача. Три участка общей площадью 360 га засеяны рожью.
Первый участок на 120 га меньше второго, который на 60 га больше третьего. С первого участка собрали по 26 ц с 1 га, со второго — по 24 ц, а с третьего — по 22 ц с 1 га. Сколько центнеров ржи собрали?
Краткая запись условия может быть такой (табл. 8):
Таблица 8
|
Участок |
Площадь, га |
Урожайность, ц |
|
I II III |
На 120 меньше II На 60 меньше II |
26 24 22 |
360 га
Сколько центнеров ржи собрали?
Из такой схематической записи не все учащиеся могут выявить соотношения между данными, которые необходимы для осмысления условия задачи. Чтобы условие задачи было понято всеми учащимися, учитель организует деятельность учащихся по составлению графической схемы условия задачи, например такой:
На втором этапе решения задачи учитель организует деятельность учащихся разными приемами в зависимости от целей, которые он ставит при работе над задачей.
Поиск решения задачи может осуществляться аналитическим или синтетическим путем, но осуществить поиск только аналитически или только с помощью синтеза очень трудно. Чаще всего поиск решения сюжетных задач проводится аналитико-синтетическим путем.
Анализ задачи начинается с вопроса задачи, который задает учитель учащимся. Школьники подбирают данные, с помощью которых можно ответить на поставленный вопрос. Если числовых данных в условии нет, то учитель ставит новые вопросы. К этим вопросам вновь подбираются учащимися данные задачи или ставятся учителем новые вопросы.
Такое «разложение» условия задачи продолжается до тех пор, пока дойдут до такого вопроса, для ответа на который все данные в условии есть.
Анализ может быть записан как в виде таблицы (табл. 9), так и в виде «содержательной» схемы, «поднимаясь» по которой снизу вверх приходят к ответу.
Таблица 9
|
Чтобы узнать |
Надо определить |
|
сколько центнеров ржи собрали |
какова площадь каждого участка, сколько собирали с 1 га на каждом участке (известно) |
|
какова площадь I участка |
какова площадь II и на сколько I меньше II (на 120 га) |
|
какова площадь III участка |
какова площадь II и на сколько III меньше II (на 60 га) |
«Содержательная» схема поиска решения может выглядеть так:
Из анализа получают план решения задачи. Запись решения зависит от того, какой способ решения указан. Если арифметический, то формы записи могут быть:
- вопрос с последующим действием;
- действие с последующим объяснением;
- запись решения с предшествующим пояснением;
- числовое решение без всякого текста.
При решении задачи алгебраическим способом существенное значение имеет выбор величины за неизвестное, с помощью которого можно выразить остальные (или часть остальных) величины, входящие в задачу, и установить зависимость между данными задачи, которая даст возможность составить уравнение. для многих задач за неизвестное можно принимать величину, которую требуется найти; тогда ответ на вопрос задачи получается без дополнительных вычислений.
При решении сюжетной задачи часто используют сочетание арифметического и алгебраического способов решения. В силу этого форма записи решения каждой части будет разной.
Задача 3. Оформите решение приведенной выше задачи, выбрав способ решения.
Анализ задачи приводит к выводу, что задачу рационально решить сочетанием алгебраического и арифметического способов, а именно нахождение площади каждого участка осуществить алгебраическим способом, а затем арифметически легко найти, сколько центнеров ржи собрали с трех участков вместе.
Самый трудный момент при решении задачи алгебраическим способом — мотивировка составления уравнения. Обращая внимание учащихся на графическую иллюстрацию и «содержательную» схему анализа задачи, подводим школьников к выводу, что за неизвестное следует принять площадь П участка. Такой выбор неизвестного приводит к следующим рассуждениям:
если площадь II участка х га,
то площадь I участка (x-120) га,
а площадь III участка (х-60) га;
тогда площадь трех участков (x+x-120+x-60) га, а так как по условию задачи площадь трех участков равна 360 га, то можно составить уравнение
х+х-120+х-60=360.
При обучении учащихся решению задач алгебраическим способом целесообразно требовать от школьников проговаривания мотивировки составления уравнения. Желательно одну и ту же задачу решать, составляя различные уравнения при выборе за неизвестное различные величины, входящие в условие задачи. Такой прием позволяет сформировать у учащихся умение мотивировать составление уравнения при решении задачи алгебраическим способом.
Для рассматриваемой задачи можно предложить составить уравнения, выбрав за неизвестное: а) площадь I участка; б) площадь II участка или площадь III. Выбор неизвестного и составление уравнения можно оформить в виде таблицы 10.
Таблица 10
|
Вся площадь |
I участок |
II участок |
III участок |
Уравнение |
|
360 |
x у-60 z-120 |
x+120 у+60 z |
x+60 у z-60 |
х+х+120+х+60=360 у-60+у+60+у=360 z-120+z+z-60=360 |
Получение нескольких решений одной и той же задачи позволяет не только сравнивать эти решения, но и указывать наиболее рациональное из них.
Особое внимание уделяется проверке решения задачи. В практике школы проверке уделяют достаточно внимания, так как она помогает выяснить, правильно ли понята задача, согласуется ли найденный ответ с условием задачи. Учащихся следует познакомить с видами проверки решения задачи:
- решение задачи другим способом;
- установление факта, удовлетворяет ли полученный ответ условию задачи по содержанию.
Задание 4. Подготовьте сообщение по вопросу «Всегда ли нужна проверка при решении сюжетных задач?» (Математика в школе. - 1971. - № 3).
Последним этапом решения задачи является осмысление ответа и полная его запись.
Рассмотренная методика работы над текстовой задачей дает возможность формировать у учащихся умения записывать реальные жизненные ситуации на математическом языке, что способствует развитию логического мышления, овладению операциями мышления — анализом, синтезом, обобщением, воспитывать такие качества личности, как самостоятельность, настойчивость и творчество.
Самостоятельная работа
Приведите образцы краткой записи следующих задач:
Задача 1. За 18 дней бригада лесорубов в составе 15 человек заготовила 972 м3 дров. Сколько дров заготовит бригада из 12 человек за 25 дней при такой же производительности труда?
Оформите краткую запись условия задачи в виде таблицы.
Задача 2. Площадь, засеянная овсом и рожью, 60 га. Какова площадь, занятая каждой культурой, если ржи собрали на 440 ц больше, чем овса, снимая с каждого га по 26 ц, а урожайность овса 30 ц с 1 га?
Постройте графическую модель для мотивировки составления уравнения.
Задача 3. Совхоз посеял
сахарную свеклу за три дня. В первый день засеяли ![]() всей площади, во второй
всей площади, во второй ![]() остатка, в третий засеяли на 24 га
меньше, чем во второй. На какой площади посеяна свекла?
остатка, в третий засеяли на 24 га
меньше, чем во второй. На какой площади посеяна свекла?
Выполните графическую иллюстрацию условия задачи, проанализируйте задачу, запишите поиск решения задачи в виде «содержательной» схемы, решите задачу арифметически и алгебраически. Для первого способа проверку сделайте составлением задачи, обратной данной.
Задания выполните в аудитории. Одно из заданий сделайте на прозрачной пленке для последующего обсуждения и проверки.
Задания для домашней работы
1. Опишите методику работы над одной из задач из учебников [39], [40], [23], [24].
2. Оформите решение задачи разными способами, к одному из способов дайте запись на прозрачной пленке.
Литература: [23], [24], [39], [40], [27], [29], [93].
§ 6. ЛАБОРАТОРНЫЕ РАБОТЫ ПО ОРГАНИЗАЦИОННЫМ ВОПРОСАМ ОБУЧЕНИЯ МАТЕМАТИКЕ
К профессиональным умениям, которыми необходимо овладеть будущему учителю, относятся умения использования различных видов наглядности на уроке, а также организации контроля за деятельностью учащихся.
Большая группа умений связана с пониманием структуры урока математики, видов урока, форм организации деятельности учащихся на уроке и т. п. К этой же группе умений относится и анализ урока.
Хотя многие из этих вопросов известны из курсов педагогики и психологии, но на занятиях по методике преподавания математики эти знания получают предметную завершенность, т.е. осмысление через специфику и особенности предмета. Поэтому мы считаем необходимым конкретизировать типы уроков применительно к предмету математики, на примере посещения ряда уроков раскрыть наиболее трудные из них по форме организации, по приемам вовлечения учащихся в самостоятельную работу.
Лабораторная работа № 6
Тема. Наглядность при обучении математике в средней школе.
Цель. Актуализировать знания о принципе наглядности при обучении, раскрыть функции наглядности и правила подбора, рассмотреть виды наглядности, познакомиться с «технологией» изготовления и использования кодопозитивов.
Оборудование. 1. Наглядные пособия различных видов.
2. Образцы кодопозитивов и серий кодопозитивов для иллюстрации.
3. Раздаточный материал к лабораторной работе (нарезанные листы пленки, перья «Редис», тушь «Кальмар», линейки с «откосом»).
План
1. Рассмотреть принцип наглядности, его особенности при обучении математике, кратко раскрыть правило подбора и использования наглядности.
2. Выполнить обзор наиболее распространенных видов учебного оборудования.
3. Познакомиться с комплексным использованием учебного оборудования.
4. Изготовить необходимые кодопозитивы.
5. Выполнить самостоятельную работу.
6. Подвести итог.
Основное содержание
Функции наглядности. Наглядность обучения — один из принципов советской дидактики.
Применение наглядности при обучении математике имеет корни в теории познания и согласуется с методологией математики.
Можно условно выделить три этапа познания: восприятие, представление и абстрактное мышление. Условно процесс познания можно разбить на две ступени: чувственную (восприятие и представление) и логическую (переход от представления к понятию с помощью обобщения и абстрагирования). Чувственная ступень соответствует первому этапу пути познания, и здесь роль наглядности весьма важна: она используется для извлечения знаний о внешних свойствах математических объектов, о взаимосвязи объектов, об их сходстве и различии. На третьем этапе познания наглядность дает возможность показать учащимся глубинные связи между свойствами математических объектов, создать правильный образ.
Основным правилом подбора и использования наглядности психологи считают выявление действий, которые вызовут у учащихся представляемые средства наглядности, и определение действий, которые должны выполнять учащиеся, чтобы сознательно овладеть учебным материалом.
В своей работе учитель должен иметь в виду, что средства наглядности имеют различные функции в процессе обучения.
Отбирая средства наглядности к уроку, учитель должен ясно представлять, какую именно функцию эти пособия должны выполнять в учебном процессе, какую роль они должны сыграть в решении учебных задач.
Основными видами наглядности, которые находят широкое применение в обучении математике, являются:
- натуральная наглядность;
- изобразительная наглядность;
- символическая наглядность.
Основные признаки наглядности при обучении математике высказаны В. Г. Болтянским [30]. Это правильное изоморфное отражение существенных черт явления и простота восприятия.
Изоморфизм — соответствие между объектами, выражающее тождество их структур.
Основные средства наглядности. 1. Таблицы. Одним из самых распространенных средств наглядности являются таблицы, которые несут различную смысловую нагрузку. Одни из них можно отнести к изобразительной наглядности (рисунки, фотографии и др.), другие — к символической наглядности (графики, чертежи, схемы, диаграммы и др.).
Таблицы, которые используются при выработке умений и навыков, получили название рабочих таблиц; например, при изучении свойств функций целесообразно сопоставлять аналитическую запись свойства с изображением его графически. К рабочим таблицам следует отнести таблицы, на которых даны схемы алгоритмов, графы.
Использование схем алгоритмов в обучении дает возможность организовать самостоятельное изучение отдельных вопросов темы, систематизировать знания учащихся при повторении, показать взаимосвязи различных разделов курса математики, установить межпредметные связи и др.
Широко применяются и справочные таблицы: таблицы квадратов, кубов, натуральных чисел и др.
В последнее время широкое распространение получили экранные средства обучения — кинофрагменты, кинофильмы, диафильмы, диапозитивы, кодопозитивы и др.
Задание 1. 1) Составьте
рабочую таблицу, показывающую возможные положения графика квадратичной функции
в зависимости от коэффициента а, b и с в задании функции ![]() . 2) Составьте таблицу для возможных
значений суммы двух чисел а и b с учетом их знака и модуля.
. 2) Составьте таблицу для возможных
значений суммы двух чисел а и b с учетом их знака и модуля.
2. Кинофрагменты и кинофильмы эффективно используются при изучении вопросов, связанных с понятиями функции, производной и интеграла, решением задач на построение методом подобия, графическим решением уравнений (неравенств), систем уравнений (неравенств), построением графиков функций, в частности тригонометрических, вычерчиванием изображений пространственных фигур.
Задание 2. Продумайте формы организации просмотра учебного фильма «История пятого постулата» и разработайте набор вопросов по использованию информации фильма при изучении аксиомы о параллельных прямых.
3. Диафильмы. На одном уроке или на нескольких последовательных уроках при объяснении логически завершенного материала может оказаться, что для решения поставленной учебной задачи требуется иллюстрировать материал большим количеством примеров. В этом случае целесообразно использовать диафильм. Кадры диафильма могут быть снабжены подписями (именно такие диафильмы в основном выпускаются), а могут не иметь подписей. Такие кадры могут быть использованы не только при объяснении, но и при обобщении и закреплении материала.
Задания для устной работы , дополнительный материал, раздаточный материал и различные способы решений задачи лучше всего предлагать учащимся на диапозитивах, так как их можно менять местами в соответствии с выбранной формой изложения.
Задание 3. 1) Из диафильма «Как устроена теорема» вычлените кадры, раскрывающие структуру простой теоремы, и разработайте несколько контрпримеров, помогающих сознательно осмыслить структуру теоремы. 2) Из набора диапозитивов «Углы» отберите последовательность диапозитивов для классификации углов по величине.
4. Магнитная доска. Часть классной доски, покрытая листом железа, и набор магнитов, с помощью которых крепятся фигуры на доске, называют магнитными средствами обучения. Легкое крепление фигур, свободное перемещение создают специфику их использования и важные дидактические возможности. Каждый учитель может изготовить магнитные средства и использовать их в обучении.
Задание 4. Магнитную доску покройте координатной сеткой и с помощью металлических шашечек проиллюстрируйте быстрое получение основных точек графиков линейной, квадратичной функций. Каковы возможные эффективные случаи использования магнитной доски?
5. Тетрадь с печатной основой характеризуется дидактической направленностью действий, которые должен выполнить ученик, чтобы получить результат. Ученик выполняет серию заданий, в которых степень его самостоятельности растет. Это дает возможность формировать требуемое умение и приучать школьника к принятой форме записи, индивидуализировать работу, осуществлять дифференцированный подход.
Задание 5. Запишите
многочлен ![]() в виде разности двух многочленов.
в виде разности двух многочленов.
Решение
а) ![]() ;
;
б) ![]() ;
;
в) ...; г) ...; д) ... .
Всего ... решений. Существуют ли другие решения?
Ответ: ... (да, нет).
Другим примером средств обучения, обеспечивающих учет индивидуальных особенностей учащихся, являются карточки с заданиями.
6. Объемные модели геометрических фигур. Все рассмотренные выше средства наглядности являются плоскостными изображениями. Существуют еще объемные модели геометрических тел и приборы. Модели геометрических тел могут быть картонные, деревянные, каркасные. Все модели дают возможность правильно формировать пространственное представление, что играет важную роль в изучении стереометрии.
7. Счетные приборы (микрокалькуляторы, ЭВМ). О работе этих приборов учащиеся получают представление на уроках курса «Основы информатики и вычислительной техники».
8. Кодопозитивы. Материалы, которые показывают через кодоскоп, называют кодопозитивами. Они аналогичны диапозитивам. Использование кодопозитива возможно при актуализации знаний, при проведении устного счета (в этом случае один из учеников пишет ответы на пленке), при построении сечений многогранников и т.п.
Так как кодопозитивы централизованно не изготовляются, то учителю необходимо владеть «технологией» изготовления хорошо «читаемых» кодопозитивов и дающих возможность правильно их использовать в учебном процессе. Поэтому необходимо овладеть рядом умений по изготовлению кодопозитивов.
Задание 6. Выполните все последовательные этапы изготовления кодопозитивов:
1. На листе миллиметровой бумаги (или на бумаге с удобным графлением) начертите прямоугольник. ограничивающий размеры будущего кодопозитива. Внутри этого прямоугольника расположите чертеж или текст, который должен быть перенесен на прозрачный материал.
2. Для изготовления кодопозитива лист прозрачной пленки нужно наложить на приготовленный чертеж и плотно прижать, протирая мягкой тканью (пленка электризуется и «прилипает» к бумаге).
3. Для выполнения чертежей и надписей на прозрачной пленке удобно использовать перья типа «Редис» или рейсфедер. Проводя прямые линии, следует использовать линейку с «откосом» или две линейки, накладывая их друг на друга, так чтобы образовался «козырек». Лучше всего работать тушью «Кальмар». Допущенные ошибки можно устранить, аккуратно снимая тушь влажной ватой, туго намотанной на спичку.
На полиэтиленовой пленке чертеж и надписи можно выполнять шариковой ручкой, используя пасту различных цветов.
4. Если планируется изготовление серии кодопозитивов, которые будут последовательно накладываться друг на друга, то нужно нарезать одинаковые листы пленки и продумать способ аккуратного совмещения изображений (например, можно проколоть иглой в углах всю пачку пленок вместе с чертежом; тогда каждую пленку можно будет прикреплять к чертежу кнопками, совмещая проколы).
При выполнении серии кодопозитивов на каждый следующий лист пленки наносятся только дополнительные линии, не повторяющие того, что было на предыдущих кодопозитивах.
Серию кодопозитивов удобно скрепить тетрадочкой (сшить или использовать скрепки). Показ начинается с последней страницы, ее удобно прижать стеклом.
Можно в каждом кодопозитиве пробить отверстие, соответствующее расположению штифтов кодоскопа. Тогда кодопозитивы нанизываются на эти штифты, обеспечивая хорошее совмещение изображений.
Комплексы учебного оборудования. Как отмечает В.Г. Болтянский, комплекс учебного оборудования по теме должен давать педагогический эффект, близкий к максимально возможному. Под единым комплексом учебного оборудования понимают объединение предметов общим содержанием, общностью методики изложения темы, способными охватывать все стороны учебного процесса.
Укажем основные условия, при которых использование комплексов дает педагогический эффект, близкий к максимально возможному.
Предметы комплекса учебного оборудования должны:
- быть объединены единым содержанием, методологией, согласованы друг с другом в методическом отношении;
- соответствовать современным научным представлениям об объекте изучения, возрастным особенностям школьников;
- обладать высокой степенью наглядности;
- позволять при необходимости индивидуализировать приобретение навыков в решении задач, построении алгоритмов;
- обеспечивать высокую научную организацию труда учителя и учащихся;
- поддерживать высокий уровень внимательности и активности школьников;
- удовлетворять психофизиологическим и эстетическим требованиям.
Комплекс оборудования по теме может быть составлен различными способами.
Самостоятельная работа
Изготовьте серию кодопозитивов, разработайте методику работы с ними на уроке.
Варианты заданий
Литература: [30], [21], [93], [95], [109], [125].
Лабораторная работа № 7
Тема. Формы, способы и средства контроля и оценки знаний и умений учащихся. Нормы отметок.
Цель. Выделить виды, формы, средства контроля знаний и умений учащихся; установить требования к контролю знаний и умений учащихся; установить, в чем заключаются подготовка учителя к контрольной работе и анализ результатов такой работы.
Оборудование. 1. Наборы заданий к разным этапам работы (тесты, образцы проверочных работ и т.п.). 2. Контрольные (самостоятельные) работы, выполненные учащимися в школе. 3. Таблицы на кодопозитивах для анализа результатов контрольной работы.
Основное содержание
Контроль знаний и его типы. О контроле знаний и умений можно говорить, имея в виду следующее.
С точки зрения внешней структуры организации процесса обучения контроль — это часть процесса обучения. Известно, что любая полноценная деятельность, в том числе и обучение, состоит из трех частей: ориентировочной, исполнительной и контрольной.
С точки зрения внутренней сущности контроль — это выявление и сравнение (на определенном этапе обучения) результата учебной деятельности с требованиями, которые задаются к этому результату программой (иначе это — соотнесение достигнутых результатов с запланированными целями обучения). Причем контроль знаний и умений конкретного ученика предусматривает оценку этих знаний и умений только по результатам его личной учебной деятельности.
В последующем будем иметь в виду в основном вторую точку зрения на понятие «контроль знаний и умений учащихся».
В зависимости от того, кто именно осуществляет контроль за результатами деятельности учащегося, выделяют следующие три типа контроля:
- внешний (осуществляется учителем над деятельностью ученика);
- взаимный (осуществляется учеником над деятельностью товарища);
- самоконтроль (осуществляется учеником за собственной деятельностью).
Основная цель контроля знаний и умений состоит в обнаружении достижений, успехов учащихся, через призму которых рассматриваются недостатки в осуществлении учебной деятельности, пробелы в знаниях и т.п.; в указании путей совершенствования, углубления знаний, умений, с тем чтобы создавались условия для последующего включения школьников в активную творческую деятельность.
Конкретизация этой цели связана с
установлением качества усвоения учащимися материала, предусмотренного программой по математике для средней школы (установление полноты, характера выполнения учащимися заданий учителя; выявление соответствия достигнутого школьниками уровня овладения изучаемым материалом принятым нормам или образцам);
определением мер корректирования знаний и умений учащихся; научением школьников приемам взаимоконтроля и самоконтроля, формированием потребности в самоконтроле;
воспитанием ряда качеств личности, например ответственности за выполняемую работу, инициативы и др.
Если перечисленные цели контроля знаний и умений учащихся реализованы, то можно говорить о том, что контроль выполняет следующие функции:
- выявления и диагностики результатов обучения (иногда говорят о контролирующей и диагностической функциях);
- образовательную (обучающую), связанную с повышением качества усвоения знаний, их систематизацией, формированием приемов учебной работы;
- стимулирующую (развивающую), связанную с созданием необходимой основы для стимулирующих содержательных оценок деятельности учащихся, для развития познавательной активности школьников;
- воспитательную, направленную на воспитание у каждого чувства ответственности за результаты учения, на формирование познавательной мотивации;
- управления процессом усвоения знаний, умений, его коррекции (иногда эту функцию называют прогностической, имея в виду возможность получения в процессе контроля опережающей, носящей вероятностный характер информации о некоторых особенностях учебно-воспитательного процесса).
В процессе контроля знаний и умений учащихся выделяются следующие компоненты:
- уточнение целей изучения данного отрезка учебного материала и установление конкретного содержания контроля;
- выбор видов, форм, способов и средств контроля, соответствующих поставленным целям;
- различные способы выражения результатов контроля: оценка и отметка.
Рассмотрим первый из указанных компонентов.
Установление конкретного содержания контроля зависит от целей изучения данного отрезка учебного материала и связано с определением, во-первых, информационно-предметного состава того знания, которое должно быть сформировано (понятия, факты, теоремы, алгоритмы, методы), т.е. с выделением объектов контроля; во-вторых, операционного состава этого знания, т.е. с указанием тех действий, в процессе выполнения которых учащимися и должно проявляться усвоение того или иного объекта контроля.
Как описать эти цели и содержание, чтобы они служили основой для разработки средств, заданий и т.п., для контроля знаний и умений учащихся?
Можно указать различные подходы к такому описанию. Рассмотрим два из них.
Первый связан с указанием тех качеств, которые должны быть присущи сформированным в результате обучения знаниям и умениям учащихся: полнота, глубина, обобщенность, осознанность и др. Для контроля знаний специально разрабатываются такие средства, реализация которых обнаруживает наличие или отсутствие заранее зафиксированных качеств.
Задание 1. Разработайте систему упражнений, на основе выполнения которых можно проверить, достаточно ли полно усвоено учащимися правило сложения обыкновенных дробей.
Например, для проверки качества усвоения правила умножения десятичных дробей может быть использован следующий набор упражнений:
![]() .
.
Второй подход к описанию целей изучения определенного отрезка учебного материала связан с указанием уровней усвоения знаний и соответствующих им видов деятельности. Известно, что психологи выделяют следующие уровни усвоения: узнавание, запоминание, воспроизведение материала; понимание и использование в сходной с уже рассмотренной ситуации; самостоятельное преобразование материала, перенос знаний на решение широкого круга задач в новую ситуацию.
Задание 2. Разработайте задания для проверки изучения способов решения квадратных уравнений на уровне применения в знакомой ситуации и на уровне переноса знаний в новую ситуацию.
В зависимости от требований программы учитель должен заранее планировать тот уровень усвоения знаний, который будет подлежать контролю, и ставить об этом в известность учащихся.
Заметим, что данные об обязательных результатах обучения, публикуемые на страницах журнала «Математика в школе», указывают тот уровень усвоения математического материала, который считается допустимым и соответствует удовлетворительному усвоению знаний и умений.
Виды, формы и средства контроля. В зависимости от различных оснований деления можно говорить о различных подходах к указанию видов контроля
Например: 1) Если в процессе контроля основное внимание уделять деятельности контролируемого субъекта, то выделяются: контроль по конечному результату (обращаем большее внимание не на ход, состав деятельности, а на ее результат); пошаговый контроль (следим за выполнением отдельных операций, которые определяют то или иное действие); контроль, связанный с установлением определенных параметров деятельности. Очевидно, с точки зрения обучающего эффекта предпочтительнее пошаговый контроль, так как в его процессе ученик осознает сущность и характер деятельности.
2) По месту в процессе обучения можно выделить следующие виды контроля знаний и умений учащихся: текущий (осуществляется в ходе процесса учения школьников); итоговый по теме (тематический); итоговый по курсу обучения. Иногда текущий контроль подразделяют на предварительный (его цель — установить готовность учащихся к изучению нового материала), ежедневный, периодический.
Формы контроля знаний и умений учащихся выделяются в соответствии с формами обучения: массовой (иногда в ней выделяют групповую и фронтальную) и индивидуальной.
Можно указать и конкретные формы, используемые в практике работы школы, которые могут быть отнесены как к массовой, так и к индивидуальной. Это зачет, фронтальный, индивидуальный опрос, контрольные работы, сочинения, диктанты.
Замечание. Говоря о массовом контроле, используем этот термин условно: в том смысле, что контролем охвачен не один ученик. Естественно, задание каждый ученик выполняет индивидуально (иногда выполнение задания может быть поручено группе учащихся).
Выделяют различные способы контроля знаний и умений школьников: письменный, устный, практический (связан с выполнением различного рода лабораторных и практических работ).
Говоря о средствах контроля знаний и умений, чаще всего имеют в виду задание или несколько заданий, которые предлагаются учащимся с целью выявления соответствующих поставленным целям результатов обучения.
В основу классификации таких средств может быть положена форма ввода ответа на контролирующее задание.
В этом случае выделяются:
- задания свободного выбора ответа и
- тесты (ввод ответа определенным образом ограничивается).
Рассмотрим каждую из этих групп.
Задания свободного выбора предусматривают свободное конструирование ответа учащихся. Такие задания в зависимости от характера учебно-познавательной деятельности учащихся при их выполнении могут быть разделены на
вопросы (в основе — деятельность воспроизведения);
задачи (выполнение этих заданий предполагает сформированность действий, составляющих основу деятельности по решению задачи).
Тесты делятся на два вида: тесты на припоминание и дополнение, избирательные.
Тесты первого вида представляют собой задания учащимся заполнить пропуски в предложенном им связном тексте (например, тетрадь с печатной основой).
Избирательные тесты делятся на альтернативные, перекрестного выбора и множественного выбора.
Альтернативный тест — это задание, выполнив которое ученик из двух предложенных ему ответов должен выбрать один (по его мнению, правильный).
Задание 3. Разработайте альтернативный тест для проверки правильности найденных значений арифметического квадратного корня.
Примеры
1) Является ли 2 корнем уравнения ![]() ?
?
Ответить: да, нет.
2) Верно ли суждение: диагонали четырехугольника взаимно перпендикулярны — значит, этот четырехугольник ромб?
Ответить: да, нет.
Тест перекрестного выбора (соответствия) представляет собой несколько заданий, после выполнения которых ученик устанавливает соответствие полученных им результатов предполагаемым результатам, записанным в произвольном порядке (число заданий и число предлагаемых учащимся ответов совпадают).
Пример. Решить неравенства:
1) 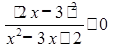 ; 2)
; 2) 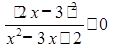 ; 3)
; 3)  ; 4)
; 4) ![]() .
.
Ответы: 1) ![]() или
или ![]() (иначе
(иначе ![]() , но
, но ![]() ). 2)
). 2) ![]() .
.
3) ![]() или
или ![]() (
(![]() , но
, но ![]() ). 4)
). 4) ![]() или
или ![]() .
.
Тест множественного выбора состоит из задания и списка ответов (среди ответов — один правильный). Ученик должен выбрать из этого списка тот ответ, который, по его мнению, является правильным.
Примеры
1) Найти значение выражения 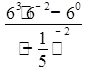 .
.
Ответы: ![]() ; не знаю.
; не знаю.
2) Указать, какая из алгебраических дробей не имеет
смысла при ![]() :
:
![]() .
.
Задание 4. Разработайте
тесты перекрестного выбора и множественного выбора для проверки решения
неравенства ![]() .
.
Что следует иметь в виду учителю, осуществляющему отбор и составление средств контроля знаний и умений учащихся?
Содержание задания должно соответствовать цели контроля (контролируемому результату).
Каждый ученик должен понимать задание однозначно. Задания следует составлять таким образом, чтобы была возможность с их помощью получить максимум информации об объекте контроля. Нужно также заметить, что средства контроля целесообразно снабжать инструкцией, которая позволила бы любому осуществляющему контроль однозначно оценивать выполнение учеником каждого задания.
Оценка и отметка. Как указывалось выше, процесс контроля знаний и умений учащихся связан с оценкой и отметкой. Эти понятия следует различать. Оценка — это процесс, действие (деятельность) оценивания, которое осуществляется человеком. Отметка выступает как результат этого процесса (результат действия), как его условно формальное выражение.
Можно говорить о различных способах оценивания в зависимости от того, с чем производится сравнение действий ученика при оценке. Если сравниваются действия, производимые учеником в настоящем, с аналогичными действиями, произведенными этим же учеником в прошлом, то мы имеем личностный способ оценивания. Если сравнение происходит с установленной нормой (образцом) выполнения действий, то обращаемся к нормативному способу. В случае сопоставительного способа оценивания происходит сравнение действий ученика с аналогичными действиями, которые выполняют другие ученики.
Понятно, что в текущей учебной работе учитель, как правило, использует личностный способ оценивания; при подведении итогов изучения темы, итогов четверти и т.д. - нормативный. Сопоставительный способ оценивания использовать не рекомендуется.
Оценка и отметка определяются знаниями и умениями ученика, которые он показал в процессе контроля. Одним из показателей, по которому учитель имеет возможность судить об этих знаниях, умениях, служат погрешности, допущенные учащимися при работе со средствами контроля, предложенными учителем.
Погрешности делят на ошибки и недочеты.
Ошибка — это погрешность, свидетельствующая о том, что
ученик не овладел теми знаниями и умениями (связанными с контролируемым
разделом, темой), которые определены программой по математике для средней
школы. Примерами ошибок будут следующие: ![]() ; неравенство
; неравенство ![]() равносильно неравенству
равносильно неравенству ![]() и др.
и др.
Недочетом считают погрешность, указывающую либо на недостаточно полное, прочное усвоение основных знаний и умений, либо на отсутствие знаний, которые программой не относятся к основным. К недочетам относят также неаккуратную запись, небрежное выполнение рисунка или оформления решения задачи и т.д.
Приведенное деление погрешностей на ошибки и недочеты является условным, и это нужно иметь в виду в процессе оценивания. Следует помнить, что размытость границы между ошибкой и недочетом (что значит «недостаточно полное, прочное усвоение основных знаний и умений», как установить меру «этой недостаточности») может быть одной из причин необъективной оценки (а как следствие — и отметки) знаний и умений ученика. В зависимости от объекта контроля, от конкретных обстоятельств погрешность, которая допущена учеником, может быть отнесена учителем к разряду ошибок или недочетов. Например, ученик допустил погрешность при выполнении умножения десятичных дробей: подписал одно из неполных произведений под несоответствующим ему разрядом множителей. На этапе изучения и усвоения указанного действия эта погрешность считается ошибкой. Если же она допущена при решении достаточно сложной задачи (алгебраической, геометрической) и не привела к искажению смысла предложенного ученику задания, способа его выполнения, то ее можно отнести к недочетам.
Можно говорить и о других показателях, с помощью которых учитель судит о знаниях и умениях учащихся. Это изложение изученного материала грамотным языком в определенной логической последовательности, обращение к иллюстрации теоретических положений конкретными примерами, правильное применение теории в новой для ученика ситуации (например, при выполнении практического задания), самостоятельность в процессе выполнения задания и т. д.
Задание 5. Изучите нормы отметок и соотнесите их с обязательными результатами обучения математике.
Подготовка к контрольной работе. Во-первых, нужно четко определить объект контроля и цель предстоящей контрольной работы. И объект, и цель должны быть доведены до сведения учащихся (учащиеся должны их понять). При этом цель должна быть конкретной: иначе не будет возможности говорить о том, достигнута она или нет. Например, объектом контроля усвоения учащимися темы «Функции и их графики» ([6]) могут служить понятие функции и способы задания функции. Цель, которую учитель может преследовать, связана с установлением: 1) понимания учащимися свойства однозначности (свойства, характеризующего именно функциональную зависимость между переменными x и у) и умения проверять наличие этого свойства у конкретных зависимостей; 2) умения осуществлять переход от способа задания функции формулой к табличному и графическому способам.
Во-вторых, в соответствии с установленными объектом контроля и целью контрольной работы требуется отобрать средства контроля. В данном конкретном случае такими средствами могут быть как задания со свободным выбором ответа, так и тесты. В зависимости от вида заданий нужно продумать, каким образом ученик должен оформить решения этих заданий (перед выполнением работы следует специально обратить на это внимание учащихся).
Задания какого содержания можно использовать? Очевидно, в первую очередь это будут задания, связанные с выполнением действия «подведение под понятие» (следует предусмотреть примеры зависимостей между двумя переменными, которые будут функциями, и зависимостей, для которых не будет выполняться свойство однозначности соответствия значений переменных). Например: является ли функцией зависимость между 1) переменной y (площадь прямоугольника) и переменной x (длина прямоугольника), если известно, что ширина этого прямоугольника на 7 см короче длины? 2) переменными : a и b, если она задана следующим образом:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ? В каждом случае ответ обосновать.
? В каждом случае ответ обосновать.
Заметим, что указанные виды заданий могут быть
предложены учащимся и для зависимостей, которые заданы таблицей, графиком.
Учащимся могут быть предложены также примеры объектов, не являющихся функциями
в силу того, что не установлена зависимость между двумя переменными. Например:
а) ![]() ; б)
; б) ![]() и т.д.
и т.д.
Во вторую очередь в контрольную работу должны войти
задания на построение таблицы, графика, задающих функцию, если известна
соответствующая формула (очевидно, что выполнение таких заданий предусматривает
и умение учащихся по данному значению аргумента находить соответствующее
значение функции). Примером такого задания может служить следующее: зависимость
между переменными х и у задана формулой ![]() . Известно, что аргумент принимает
значения
. Известно, что аргумент принимает
значения ![]() (и только эти значения). Будет ли
указанная зависимость функцией? Составьте таблицу и постройте график, задающие
эту зависимость.
(и только эти значения). Будет ли
указанная зависимость функцией? Составьте таблицу и постройте график, задающие
эту зависимость.
Заметим: чтобы содержание средств контроля соответствовало поставленным целям, учитель должен обратить внимание на все тонкости решения отбираемых заданий, предусмотреть возможные ошибки учащихся (которые могут свидетельствовать либо о непонимании отдельных элементов материала, усвоение которого контролируется, либо о несформированности у учащихся ряда операций, определяющих то или иное контролируемое умение).
В-третьих, учитель должен продумать, каким образом он будет осуществлять оценку выполнения учащимися контрольной работы, какие возможные погрешности будут отнесены к ошибкам, недочетам. Критерии оценки должны быть хотя бы в общих чертах известны учащимся.
Задание 6. Проанализируйте темы: «Сложение десятичных дробей» и «Равные треугольники» - и отберите возможные средства контроля качества усвоения этого материала.
Проверка контрольной работы и анализ результатов
Задание 7. Проведенную в школе контрольную (проверочную самостоятельную) работу проверьте коллективно (каждый студент проверяет одну-две работы). Классифицируйте в каждой работе ошибки, а затем выполните анализ всей работы.
Анализ результатов выполненной учащимися контрольной работы может идти в двух направлениях.
Можно говорить о количественном анализе. Данные для такого анализа удобно представить в виде таблицы (табл. 11).
Таблица 11
|
Класс |
Количество учащихся в классе |
Количество учащихся, выполнивших работу |
Отметка |
Правильно выполнил задания (по номерам) |
|||||||
|
5 |
4 |
3 |
2 |
1 |
1 |
2 |
... |
5 |
|||
|
1 |
2 |
3 |
4 |
5 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Информация, представленная в графе 5, может быть несколько иного содержания, например: число учащихся, владеющих определенными умениями (конкретные умения указываются в соответствующих столбцах таблицы); число учащихся, допустивших ошибки определенного вида, и т.п.
Анализ количественных результатов контрольной работы проводится с целью установления общей картины, характеризующей усвоение учащимися изученного материала.
Очевидно, что данные количественного анализа не позволяют «выйти» на конкретного ученика, установить уровень владения им учебным материалом, степень продвижения в учении и т.д. Такую возможность представляет качественный анализ. Информация, которая подвергается качественному анализу, должна включать данные о выполнении каждого задания предложенной контрольной работы каждым учеником класса (виды допущенных учеником погрешностей, затруднения в выполнении отдельных операций той деятельности, которую осуществляет ученик, и т. п.). Такие данные фиксируют в таблице (см. табл. 12). Содержание ее основной части свидетельствует об основных ошибках учащихся, допущенных при выполнении отдельных заданий работы; в зависимости от цели, которую ставит перед собой учитель, в содержательном отношении эта часть таблицы может дополняться или меняться.
Таблица 12
|
Фамилия учащегося |
Задание 1 |
|||
|
Виды ошибок |
||||
|
Неверно найдено значение функции по значению аргумента (вычислительная ошибка) |
Неверно найдено значение функции по значению аргумента (не знает принципа решения задачи «-», верно «+») |
Неверно построена точка, принадлежащая графику функции «-», верно «+» |
И др. |
|
|
Акимов А. |
- |
+ |
- |
|
|
|
|
|
|
|
Основная цель количественного и качественного анализа результатов контрольной работы состоит не только в установлении уровня усвоения учащимися формируемых знаний и умений, но и (в большей степени) в определении путей, средств, конкретных приемов повышения качества такого усвоения. Поэтому одним из результатов анализа и должен быть вывод о том, какую работу, на каком конкретном содержании, как и с какими учащимися следует провести, чтобы добиться усвоения ими материала на требуемом уровне.
Следует также подчеркнуть, что анализ результатов контрольной работы может способствовать получению выводов об особенностях своей деятельности по организации усвоения школьниками учебного материала. Это очень важно с точки зрения формирования, совершенствования методических умений учителя.
Самостоятельная работа
1. Составьте контрольную работу по одной из тем курса алгебры VII-IX классов. Укажите конкретную цель этой работы и поясните, почему в ней представлены задания именно такого содержания (тема указывается преподавателем).
2. Ориентируясь на нормы отметок, оцените 3-4 контрольные работы учащихся и проведите анализ полученных результатов.
Литература: [93], [112], [81], [77].
Лабораторная работа № 8
Тема. Конспект урока по математике. Общие методические требования к составлению конспекта урока.
Цель. Обобщить сведения об основных типах уроков, рассмотреть наиболее распространенные типы уроков математики; разъяснить требования к анализу уроков; познакомиться со схемой записи урока, составить конспект посещенного урока.
Оборудование. Образцы конспектов уроков.
Основное содержание
Урок — основная организационная форма учебного процесса.
Говоря об уроке, обычно имеют в виду логически законченный, целостный, ограниченный определенными рамками времени отрезок учебно-воспитательного процесса. В нем представлены в сложном взаимодействии все основные элементы учебно-воспитательного процесса: цели, содержание, средства, методы, организация.
Выделенные элементы учебно-воспитательного процесса можно положить в основу классификации уроков.
Например, по основной дидактической цели уроки можно разделить на
урок ознакомления с новым материалом;
урок закрепления изученного;
урок проверки знаний, умений и навыков учащихся.
Возможен (и довольно часто применяется) так называемый комбинированный урок. Обычно в рамках этого урока осуществляется ознакомление и закрепление нового материала.
Структура уроков различных типов определяется основной дидактической целью.
Урок ознакомления с новым материалом. Основная дидактическая цель: ввести понятие, или установить свойства (признаки, отношения), или построить правило (алгоритм) и др.
Этапы урока:
Урок закрепления знаний. Основная дидактическая цель: сформировать определенное умение, или систематизировать знания по теме.
Этапы урока:
Урок проверки знаний, умений и навыков. Основная дидактическая цель: выяснить уровень усвоения учащимися учебного материала.
Этапы урока:
Перечислим основные методические требования к уроку математики. Они помогут правильно составить конспект урока и проанализировать урок.
Все перечисленные выше требования целесообразно иллюстрировать на примере урока ознакомления с новым материалом по теме «Графики» (VI кл.). Обращать особое внимание на «технологию» реализации того или иного требования.
Показать фрагмент оформления конспекта урока по теме «Графики».
Конспект урока — модель урока. Он предполагает описание деятельности учителя и ожидаемой деятельности учащихся с возможными вариантами.
Конспект урока математики в VI классе
Тема. Графики.
Цели урока. Образовательная — ввести понятие графика, познакомить с установлением характеристик различных процессов на основе анализа их графиков;
развивающая — формировать умение анализировать явление, описанное на графическом языке;
воспитательная — формировать у учащихся наблюдательность.
Оборудование. Таблица по теме «Графики», кодопозитивы к устной работе и к объяснению нового материала, линейки и карандаши.
План проведения урока
Ход урока
3. Подготовка к изучению нового материала
Задача. Актуализировать знания о нахождении координат точек на плоскости и умение читать диаграммы.
|
Учитель |
Ученик |
Запись на доске |
Запись в тетради |
Примечание |
|
Устно ответить на вопросы по рисунку: 1) Какие координаты имеют точки А, В, С? 2) Найдите точки, абсциссы которых равны 0; 1; -1
3) Какие точки имеют ординату 0; -1; -2; 1?
На рисунке вы видите диаграмму движения велосипедиста. Она показывает путь, который проехал велосипедист за различные промежутки времени. Ответьте на вопросы: 1) Сколько километров проехал велосипедист за 1 (2, 3, 4) ч? 2) Сколько он проехал за 2,5 ч? |
А (0; 2) (возможная ошибка А (2; 0)), В (2; 2), С (3; 0) Точки с абсциссой 0: А, К, О (могут не назвать точку О); с абсциссой 1: L; с абсциссой -1: D. Точки с ординатой: 0: Е, О, С (обратить внимание на координаты точки O); с ординатой -1: К; с ординатой -2: нет точек; с ординатой 1: D
За 1 ч он проехал 18 км, за 2 ч — 36 км, за 3 ч — 54 км, за 4 ч — 72 км По диаграмме не можем узнать, сколько километров проехал велосипедист за 2,5 ч |
|
|
Самостоятельная работа
Записать разобранный на занятии конспект урока по теме «Графики» по предложенной схеме.
Литература: [39], [40], [97], [98], [23], [24].
Лабораторная работа № 9
Тема. Урок математики. Посещение урока в V-VI классах и его анализ.
Цель. Научиться наблюдать в классе урок, записывать и анализировать его по предлагаемой схеме под руководством преподавателя.
Оборудование. Примерная схема комплексного анализа урока.
Основное содержание
Школа № ... Класс ... Учитель ...
Дата записи урока ...
Тема. ...
Цель и задачи урока ... (заполняется после анализа урока).
Оборудование. ...
Ход урока
|
Учитель |
Ученик |
Примечание |
|
|
|
|
Анализ посещенного урока
1. Определить «узловые» моменты урока: место данного урока в системе уроков по теме; цель и задачи урока; тип и структуру урока.
2. Провести анализ каждой структурной части урока: определить, какая образовательная задача решается; проанализировать содержание отобранного учебного материала и установить соответствие его поставленной задаче; отметить методы и приемы, использованные учителем (рассказ, беседа, создание проблемной ситуации, постановка проблемных вопросов и т. д.), формы организации деятельности учащихся (коллективная и индивидуальная работа, устная и письменная работа), формы и методы контроля за деятельностью учащихся.
3. Выполнить анализ дидактических и психологических особенностей урока по схеме комплексного анализа урока. Для этого ответить на следующие вопросы:
4. Сделать общие выводы по уроку: 1) организация урока; 2) достижение цели и задач урока (образовательных, развивающих и воспитательных); 3) общая оценка деятельности учителя и учащихся на уроке.
Самостоятельная работа
Составьте конспект посещенного и проанализированного урока математики.
Литература: [23], [24], [39], [40], [93], [95], [115].
Лабораторная работа № 10
Тема. Посещение урока алгебры в VII-VIII классах.
Цель. Познакомиться с возможными приемами организации самостоятельной работы учащихся на уроках алгебры.
3амечание. Для посещения выбирается такой по содержанию урок, на котором возможно показать несколько форм организации самостоятельной работы. Такими уроками могут быть уроки применения знаний, уроки, где возможно организовать коллективную и индивидуальную формы работы учащихся, уроки работы с книгой и т.п.
Основное содержание
I. При посещении урока можно наблюдать различную организацию деятельности учащихся. Например, возможен прием совместно распределенной учебной деятельности учащихся при изучении теоремы Виета (VIII класс). Способ организации учебной деятельности учащихся, при которой разные аспекты изучаемого вопроса рассматриваются различными группами учащихся класса (класс разбивается на четыре группы).
Весь класс получает задание: решить квадратное уравнение, найти сумму и произведение его корней, каждой из выделенных групп дается одно из уравнений:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
Учитель дает указания по оформлению записи в тетради: разделить страницу пополам, в левой части страницы решить предложенное уравнение, записать выполнение всех заданий.
![]() Например:
Например:
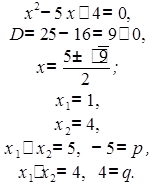
Ученики каждой группы выполняют задание, обсуждают решение. После того как группы решили задачу, они получают второе задание: сравнить сумму корней уравнения со вторым коэффициентом, а произведение корней — со свободным членом.
Далее организуется фронтальное обсуждение полученных результатов. Здесь возможно обсуждение таких вопросов:
Итогом обсуждения будет формулировка теоремы Виета.
На втором этапе изучения теоремы Виета учитель предлагает школьникам рассмотреть доказательство теоремы по учебному пособию [3], [7], [107]. Здесь может быть использован другой прием организации учебной деятельности, а именно работа учащихся парами, носящая двусторонний характер, при которой осуществляются взаимопомощь, взаимный контроль, взаимооценка, так как учащиеся должны ответить друг другу на вопросы (при ответе на вопросы заполнить правую половину страницы):
1) Чему равен дискриминант приведенного квадратного уравнения?
2) Каков знак дискриминанта, если уравнение имеет два различных корня?
3) Как записать корни уравнения в общем виде?
4) Чему равно произведение корней?
5) Сравните полученную сумму со вторым коэффициентом, а произведение — со свободным членом. Какой вывод можно сделать?
Задание 1. Какие приемы организации учебной деятельности вы «наблюдали»? С какими учебными действиями познакомились учащиеся?
II. На уроках математики необходимо уделять внимание формированию умения работать самостоятельно с книгой, которое относится к общеучебным умениям. Так, на уроке алгебры в VII классе по теме «Степень степени» может быть использован такой методический прием. Учащимся дается задание: прочитать п. 23 из пособия [2], [6], [l06]. Ответить на вопросы и решить задачи после чтения учебника.
Учитель предлагает, например, такие вопросы:
1) Что называется степенью числа а?
2) Как формулируется основное свойство степени?
3) Что называется произведением?
4) Как возвести выражение в степень?
5) Верны ли равенства ![]() ? Почему?
? Почему?
6) Как возвести степень в степень?
7) Что больше: ![]() или
или ![]() ?
? ![]() или
или ![]() ?
? ![]() или 0?
или 0? ![]() или 0?
или 0? ![]() или
или ![]() ?
?
Ответы учащихся на эти вопросы дают возможность осуществить обратную связь и установить усвоение материала и его понимание учащимися.
Задание 2. Установите, в каких темах алгебры VII класса может быть использован рассмотренный методический прием.
Ш. При работе с текстом учебника возникает опасность механического запоминания материала. Чтобы избежать этого, важно обратить внимание учащихся на цель изучения материала; указать им, что следует запомнить, а что принять к сведению; дать инструкцию по работе с текстом учебника, обратив их внимание на то, что следует записать в тетради.
Приведем пример такого методического приема при изучении преобразования произведения двух многочленов в многочлен стандартного вида.
Перед учащимися ставятся цели:
- усвоить новые знания;
- составить краткую запись изученного материала.
Работа начинается с беседы, в которой учитель обращает внимание учащихся на основные моменты их самостоятельной работы с текстом учебника, дает рекомендации (перечень рекомендаций написан на доске или спроецирован на экран).
Разделить текст на смысловые части:
- Выписать новые понятия, если они есть.
- Установить связь с ранее изученным материалом.
- Выяснить, что является главным в тексте.
- Рассмотреть рисунок 98, [6].
- Установить связь буквенной записи и графической иллюстрации.
Учитель дает время для самостоятельного чтения.
На сколько усвоен материал учащимися при самостоятельном чтении, каков уровень владения умениями, перечисленными в рекомендации, проверяет учитель во фронтальной беседе.
Беседа позволяет каждому школьнику проверить себя, выяснить, правильно ли он пользовался рекомендациями.
После первого прочтения учитель проводит более глубокую работу с каждым смысловым куском текста, и итог записывается в тетрадь после коллективного обсуждения:
- Дважды используется распределительный закон умножения относительно сложения.
- Чертеж показывает, что порядок замены скобок безразличен.
- Вывод о тождественном равенстве произведения многочленов и суммы произведений.
- Дается предписание умножения многочлена на многочлен.
Учитель подчеркивает, что не нужно запоминать переменные, входящие в многочлены, и просит записать в тетрадях свои, отличные от переменных в учебнике.
Задание 3. Составьте вопросы для фронтальной беседы.
Самостоятельная работа
Описать приемы организации самостоятельной работы, которые увидели на уроке, приемы работы с книгой.
Литература: [2], [3], [6], [7], [106], [107], [60], [119].
Лабораторная работа № 11
Тема. Посещение урока геометрии в VII-VIII классах.
Цель. Провести наблюдение и записать деятельность учителя и учащихся на уроке; проанализировать деятельность учителя в процессе решения задачи (или работы над теоремой) с точки зрения приемов работы, используемых им на разных этапах решения задачи (или изучения теоремы); выяснить, какие умения формировал учитель у учащихся и каким образом это делал.
Работа по подготовке к посещению урока
Примерный вариант совместной деятельности учителя и учащихся при решении задач
Известно, что в методике преподавания математики процесс решения задачи состоит из четырех основных этапов:
I. Мотивация решения задачи и осмысление текста (содержания) задачи.
II. Поиск плана решения.
III. Осуществление плана решения.
IV. Изучение найденного решения.
Рассмотрим совместную деятельность учителя и учащихся на примере решения следующей задачи:
Дано: АК=ЕС, АЕ=СК
(рис. 11).
Доказать: 1) ![]() . 2) ВЕ=ВK.
. 2) ВЕ=ВK.
а) Мотивация решения данной задачи. Для этого может быть использован следующий прием. Учащимся предлагается рассмотреть решение задачи:
«Чтобы разделить угол В пополам с помощью только масштабной линейки, иногда поступают так: откладывают на сторонах угла В отрезки ВЕ=ВК и ЕА=КС (рис. 12); соединяют точки Е и С, А и К отрезками; в пересечении получают точку O; проводят луч ВО. Луч ВО — искомая биссектриса. Обоснуйте, почему так можно поступить. Как это можно сделать?»
Так как задача сформулирована по готовому рисунку и сразу оговорено, что дано и что требуется доказать, то работа над текстом упрощена. Она может быть сведена (для слабых учащихся) к выделению на этом рисунке цветными мелками того, что известно в задаче, и того, что требуется доказать.
б) Поиск плана решения. Выбор приема поиска решения задачи зависит от цели ее решения, которую ставит перед собой и учащимися учитель.
Деятельность учителя в процессе решения задачи: 1) общее руководство деятельностью учащихся с помощью полезных вопросов-напоминаний о том, что главным ориентиром в поиске должна быть цель решения задачи, а главными помощниками в достижении этой цели должны быть условия задачи, получаемые из них следствия и ранее полученные теоретические знания; 2) наблюдение за поиском решения задачи отдельными учащимися по чертежам и кратким записям в тетрадях, оказание помощи некоторым ученикам.
Данная задача может быть предложена учащимся в VII классе после изучения признака равенства треугольников по трем сторонам (теорема 3.6, [113]). Цель ее решения:
- учить учащихся включать данные и искомые элементы в такие фигуры (в данном случае треугольники), из рассмотрения свойств которых следует решение задачи, и, руководствуясь этим, учить выполнять дополнительные построения на чертежах;
- учить учащихся применять изученные ранее теоремы в сложных ситуациях, т.е. во взаимосвязи с другими теоремами;
- учить учащихся подводить какие-то известные условия под условия известных теорем и получать соответствующие заключения (делать соответствующие выводы).
Не останавливаясь подробно на формировании этих умений у школьников, отметим только некоторые целенаправленные вопросы, которые может задать учитель учащимся для продвижения в поиске решения задачи. Например:
1) В какие фигуры включены данные в условии задачи отрезки и углы, о которых надо доказать, что они равны?
2) Есть ли на рисунке треугольники, в которые входят все эти элементы одновременно?
3) Как получить такие треугольники? (Соединить отрезком точки А и С.)
4) Каков план решения первой части задачи? (Проводим отрезок АС, треугольники АКС и СЕА равны по трем сторонам, из равенства этих треугольников следует равенство углов АЕС и СКА.)
Аналогичная система вопросов может привести к успеху и при доказательстве равенства отрезков ВЕ и ВK. Но учитель предлагает учащимся:
3аключение: «Треугольник равнобедренный». Делаем вывод из факта принадлежности треугольника АВС понятию «равнобедренный треугольник»: боковые стороны равны; из равенства отрезков ВА и ВС, равенства их частей ЕА и КС делаем вывод о равенстве других частей ВЕ и ВК.)
Вопрос читающему: как Вы думаете, почему учитель «предложил» учащимся этот путь решения задачи?
в) Осуществление плана решения. Учащиеся самостоятельно записывают решение задачи в тетрадях, учитель оказывает необходимую помощь.
Доказательство. Проведем отрезок АС (рис. 13).
1) ![]() — по трем сторонам
(АК=ЕС, АЕ=СК — по условию; АС общая).
— по трем сторонам
(АК=ЕС, АЕ=СК — по условию; АС общая).
![]() — из равенства
треугольников АКС
и СЕА, что требовалось
доказать.
— из равенства
треугольников АКС
и СЕА, что требовалось
доказать.
2) ![]() — из равенства
треугольников АКС и СЕА.
— из равенства
треугольников АКС и СЕА.
![]() равнобедренный,
так как если в треугольнике два угла равны, то он равнобедренный.
равнобедренный,
так как если в треугольнике два угла равны, то он равнобедренный.
ВА=ВС — следует из определения равнобедренного треугольника.
ВЕ=ВК, так как ВЕ=ВА-ЕА, ВК=ВС-КС, но ВА=ВС и ЕА=КС. Следовательно, ВЕ=ВК, что требовалось доказать.
г) Изучение найденного решения и осмысление его результатов.
Возвращаемся к мотивационной задаче. Как обосновать, что ВО действительно искомая биссектриса угла В? (См. рис. 12.)
1) Каков вид треугольника АВС (рис. 14)?
2) Чтобы доказать, что ВО — биссектриса, что достаточно доказать?
3) Что значит ВР — медиана?
4) Откуда может следовать, что АР=РС?
5) Откуда следует, что углы САК и ЕСА равны?
6) Помогла ли решенная ранее задача обосновать ответ в этой практической задаче? (Да.)
7) Можно ли было по-другому доказать равенство отрезков ВЕ и ВК? Как?
8) Какие выводы из решения этих задач следует взять для
дальнейшего использования? (Еще один прием построения биссектрисы с помощью
только линейки; при поиске решения задачи целесообразно найти или построить на
этом же рисунке такие фигуры, в данном случае треугольники, в которые входили
бы и элементы, данные в условии, и элементы, о которых идет речь в заключении
задачи; одну и ту же задачу можно решить разными способами. Если есть в классе
сильные или просто очень наблюдательные учащиеся, то можно подметить и такой
факт: если на боковых сторонах равнобедренного треугольника отложить
соответственно равные между собой отрезки, то, соединив их так, как показано на
рисунке 15, получаем множество равнобедренных треугольников, например ![]() и др.)
и др.)
Мы рассмотрели деятельность учителя и учащихся на уроке при решении конкретной задачи.
Возможна и другая деятельность учителя и учащихся на каждом этапе.
На первом этапе, например, возможна деятельность (наблюдается на практике) при изучении и осмыслении условия задачи.
Учитель: Сейчас будем решать задачу № ... Задача имеет важное значение. Усвоение приема решения этой задачи поможет в поиске решения других задач. Внимательно изучите условия и требования задачи — этому помогут и выполнение вами чертежа к задаче, символическая запись условия и требования задачи. Кто хочет, может поставить обозначения на своем чертеже карандашом, после выполнения чертежа на доске можно перейти к другим обозначениям. Данные и искомые в задаче обозначьте разным цветом.
Далее после обязательной паузы к доске (если это было предусмотрено заранее или в этом возникла необходимость на уроке) вызывается ученик для выполнения чертежа и символической записи условия задачи (Дано: ... Найти: ... ).
Учитель: Есть ли вопросы по условию задачи? (С целью проверки усвоения условия задачи, возможно, слабому ученику учитель предложит воспроизвести развернутый полный текст задачи по ее краткой записи.)
После первого этапа — осмысления текста задачи — необходимо учащимся дать время для самостоятельного обдумывания плана поиска решения задачи.
На втором этапе в общем случае вопросы учителя, осуществляющего руководство деятельностью учащихся по поиску решения задачи, могут быть, например, такими:
При посещении таких уроков необходимо вдумчиво следить за деятельностью учителя и учащихся. Возможно, что отдельные учащиеся решили задачу ранее других. Обратите внимание, какую работу проводит учитель с такими учащимися:
- дает для решения другую задачу;
- просит помочь соседу;
- предлагает поменяться тетрадями с другим учеником, тоже решившим задачу, чтобы проверить свое решение.
На третьем этапе также возможно различное руководство деятельностью учащихся.
Учитель:
- предлагает учащимся самостоятельно, без вызова к доске, провести соответствующие вычисления (осуществить доказательство) в тетрадях;
- сопровождает самостоятельную работу устной проверкой промежуточных вычислений (построений, рассуждений);
- вызывает отдельных учеников (одного или нескольких) к доске для оформления записи вычислений или рассуждений;
- предлагает учащимся реализовать план решения задачи дома, а на чертеже изменяет обозначения и просит повторить основные этапы в решении задачи;
- дает новую задачу (какую? как связанную с предыдущей?).
На четвертом этапе решения задачи может осуществляться следующая деятельность:
- прикидка правильности найденного результата;
- рассмотрение особых случаев (если возможно);
- поиск другого способа решения задачи;
- обобщение: чему научились при решении данной задачи и что целесообразно запомнить из ее решения для дальнейшего использования.
После посещения урока детально осмыслите и опишите:
- приемы работы учителя для
мотивации решения задачи (изучения теоремы);
раскрытия содержания (осмысления текста) задачи, раскрытия содержания теоремы;
поиска плана решения задачи (доказательства теоремы);
- осуществление плана решения и изучение найденного решения (доказательства теоремы);
- какие выводы были сделаны учителем вместе с учащимися из решенной задачи (доказанной теоремы);
- какие бы вы предложили свои приемы работы на каждом из этапов решения задачи (изучения теоремы);
- какие специфические умения у учащихся формировали бы вы в процессе проведения данного урока.
Лабораторная работа № 12
Тема. Посещение урока в Х классе по теме «Параллельность прямых и плоскостей».
Цель. На примере темы, хорошо организованной логически, показать возможный уровень логической культуры учащихся средней школы, приемы его формирования и способы проверки. На примере данного урока рассмотреть требования к развернутому плану урока и его отличие от конспекта урока.
Основное содержание
I. Вопросы, связанные с логическими обоснованиями
Для достижения поставленной цели лабораторной работы лучше выбрать урок решения задач по данной теме в конце ее изучения.
На уроке можно решить задачи № 20 и № 33, [113].
Не будем рассматривать весь урок с его различными компонентами, которые определяются в зависимости от конкретных целей урока с учетом особенностей класса. Нам важно показать возможные подходы, обнаруживающие определенный уровень логической культуры учащихся.
3адача 20. Через данную точку пространства проведите прямую, пересекающую каждую из двух скрещивающихся прямых. Всегда ли это возможно?
Необходимо помнить, что это фундаментальная задача, в разной формулировке она присутствует во всех учебниках и задачниках, рассматривающих вопрос о скрещивающихся прямых.
Кроме того, в задаче есть два уровня решения: конструктивный (или, как иногда говорят, «на пальцах») и логически обоснованный.
Первый подход позволяет понять «идею решения», суть которой заключается в том, что две скрещивающиеся прямые в проекции на плоскости воспринимаются как пересекающиеся. Если провести прямую (мысленно) из данной точки в точку, которую мы воспринимаем как «пересечение» скрещивающихся прямых, то это и будет искомая прямая.
Строгое обоснование решения данной задачи заключает несколько этапов:
1) Пусть а и b данные скрещивающиеся прямые. С — данная точка и не лежит на прямых а и b. Искомая прямая x проходит через точку С и пересекает а и b.
2) Прямые x и а определяют
плоскость ![]() и прямые x и b —
плоскость
и прямые x и b —
плоскость ![]() .
.
3) Точка С принадлежит и плоскости α и плоскости ![]() .
.
4) Плоскость α может быть определена точкой С и прямой а (14.1). Плоскость β может быть определена точкой С и прямой b (14.1).
5) Плоскости α и β в пересечении дадут прямую x (из 2) и 4) пунктов решения), если она пересечет прямые а и b.
6) Если прямая x параллельна одной из прямых а или b, то задача решения не имеет (15.3), т. е: выходим на признак параллельности прямой и плоскости.
Выяснение с учениками обоснований всех этапов решения данной задачи и показывает уровень развития логического мышления учащихся. Поэтому задача (после поиска решения, т. е. осмысления конструктивного уровня решения) требует постановки только одного вопроса: на каком основании получаем тот или иной геометрический объект?
3адача 33. Даны две параллельные
плоскости ![]() и
и ![]() и точка А, не
лежащая ни в одной из этих плоскостей. Через точку А проведена
произвольная прямая. Пусть
и точка А, не
лежащая ни в одной из этих плоскостей. Через точку А проведена
произвольная прямая. Пусть ![]() и
и ![]() - точки пересечения ее с плоскостями
- точки пересечения ее с плоскостями ![]() и
и ![]() . Докажите, что
отношение длин отрезков
. Докажите, что
отношение длин отрезков ![]() не зависит от
взятой прямой.
не зависит от
взятой прямой.
В задаче также можно выделить несколько уровней: 1) конструктивный — изображение (рисование) геометрических отношений между объектами; 2) обоснование правомерности изображения; 3) использование теоремы 15.7 для обоснования искомого отношения; 4) исследование влияния возможных положений точки А на результат решения задачи.
В зависимости от цели урока акценты на разные уровни могут быть расставлены по-разному. Учитывая наши цели, возможно акцентировать внимание на втором .и третьем уровнях решения.
Урок с целевой установкой — проверить умение выполнять
логические обоснования — предполагает сформированность действия конкретизации.
для того чтобы убедиться, что это действие сформировано, необходимо хотя бы
один из этапов решения в задаче № 20 попросить конкретизировать, например этап
третий развернуть в аксиому ![]() .
.
II. Вопросы, связанные с требованиями к развернутому плану урока
В развернутом плане урока должны найти отражение следующие моменты: тема урока, цели урока, оборудование урока, этапы урока (в плане должны быть обозначены только те из них, которые будут на конкретном уроке).
Перечисляем возможные требования к различным этапам урока:
1. Проверка домашнего задания. В плане указать только, что проверяется, с какой целью и в какой форме.
2. Объяснение (изучение) нового материала. В плане указать: а) главную математическую суть нового материала (о чем теорема, какой вид задач, какой прием (способ, метод) вводится и т.п.); б) каким дидактическим приемом (способом, методом) будет изучаться новое: чтение книги, объяснение учителя, доклады учащихся, самостоятельное решение математических задач и т.п.; в) если доказывается новая теорема или объясняется новый прием решения задач, то доказательство теоремы и решение задачи должны быть изложены в плане.
3. Организация самостоятельной работы учащихся. В плане указать формы организации самостоятельной работы (дано задание работать с книгой и сформулированы вопросы, на которые надо в книге найти ответ; дано задание решать математические задачи и приведено предписание на кодопозитиве, помогающее и организующее решение задач; даны два варианта математических задач и указаны аналогичные, но уже решенные задачи, которыми могут воспользоваться учащиеся в случае затруднения, и т.п.; приведено решение математических задач).
4. Проверка самостоятельной работы учащихся. В плане должна быть указана одна из форм проверки: учитель соберет выполненную работу и проверит после урока; учащиеся обменяются тетрадями и выполнят взаимопроверку; на кодопозитиве будет предъявлено правильное решение, и учащиеся сверятся с образцом и т.п.
5. Домашнее задание. В плане должна быть указана цель домашнего задания, определена форма его предъявления учащимся и решены все математические задачи, которые даются им на дом.
6. Выводы по уроку. В этой части плана должно быть четко сформулировано, какие познавательные результаты получат ученики на уроке (узнают новый факт, познакомятся с операционным составом нового учебного или математического действия, научатся каким-то элементам оценки или самооценки и т.п.). Выводы по уроку тесно связаны с целями урока, но они уточняют и конкретизируют цели и, естественно, получают законченную формулировку только в реально проведенном уроке. Если поставленные цели к уроку были достигнуты, то, конечно, выводы будут их в своей основе повторять, только конкретизируя. Если же в ходе урока пришлось отклониться от основной цели, то и выводы будут другие.
Задание. На материале прослушанного и проанализированного урока напишите развернутый план урока.
Литература: [93], [95], [19], [47], [113].
Лабораторная работа № 13
Тема. Посещение школьной лекции или урока-семинара в Х-ХI классах.
Цель. Познакомиться с новыми формами организации деятельности учащихся-старшеклассников, выяснить их наиболее существенные стороны и специфику реализации.
Основное содержание
Одним из требований реформы средней общеобразовательной школы является совершенствование форм организации деятельности учащихся в зависимости от их опыта обучения в школе. В связи с этим урок как основная форма организации работы учащихся с продвижением их от I до ХI классов должен претерпевать существенные изменения.
В старших классах, особенно в X-XI, появились и активно применяются две новые формы: лекции и семинарские занятия. Эти формы часто рассматриваются в комплексе, т.е. за школьной лекцией якобы должны следовать семинарские занятия. Опыт школ Ленинграда показывает, что указанные две формы применительно к школе не обязательно рассматривать в комплексе.
Лекция может быть применена и в комплексе с последующими уроками. Лекции лучше всего использовать как вводное начало при изучении новой темы. Например, тему «Многогранники» можно начать с вводной лекции, в которой систематизировать необходимые для изучения данной темы знания по многоугольникам (понятие многоугольника и его виды, элементы многоугольника: вершина, ребро, угол, диагональ; правильные многоугольники и способы их получения и т.п.). Затем показать возможные подходы к введению понятия многогранника, раскрыть простейшие виды многогранников, показать приемы их получения, назвать их основные свойства и одно из них доказать. Далее работа может быть организована в традиционной форме проведения уроков, на которых учащиеся на основе сформулированных свойств и обобщенно представленной теории темы могут в разных формах организации (самостоятельно, под руководством учителя, коллективно и .др.) решать математические задачи и доказывать остальные свойства многогранников с использованием учебников или консультаций учителя. При таком месте лекции в учебном процессе она чаще всего должна быть монологическая, т. е. учитель не привлекает учащихся к актуализации и систематизации знаний.
Иначе может быть построена и будет выполнять другую функцию лекция в конце изучения темы. Такая лекция обобщает знания учащихся. Ее главная функция — систематизировать знания и приемы их применения по теме. Главная забота лектора в данном случае — показать связь между разрозненно изученными на уроках фактами. Причем важно отметить эту связь и с содержательной, и с организационной стороны. Например, может быть прочитана лекция по обобщению основных свойств тригонометрических функций. Итогом лекции по этой теме может быть таблица 13.
Таблица 13
|
Функция |
Свойство (наличие «+», отсутствие «-») |
|||||||
|
D(f) |
E(f) |
Четность |
Периодичность |
Нули |
Промежутки знакопостоянства |
Промежутки возрастания |
Точки экстремума |
|
|
|
|
|
|
|
|
|
|
|
Лекция может быть прочитана в диалоговой форме, и итогом ее в познавательном смысле будет не только сведение всех свойств и всех тригонометрических функций в одну таблицу, но и сравнение одних и тех же свойств разных функций и особенностей их обоснования и установления сферы применения этих свойств.
Возможна ситуация, когда после лекции будет проведен семинар.
Прежде чем рассмотреть организацию такого комплекса, отметим принципиальные особенности проведения школьного семинара.
Существенной особенностью семинара является значительно большая самостоятельность учащихся, чем на уроке, и при подготовке семинара, и при его проведении.
При подготовке семинара функции учителя сводятся к выбору темы семинара, вычленению вопросов (тем), обсуждаемых на семинаре, консультации выступающих, подготовке вопросов и заданий для всех участников семинара, подбору литературы или хотя бы ее списков для самостоятельной работы учащихся, определению способов работы учащихся на занятиях и форм осуществления контроля.
Во время проведения семинара учитель может сформулировать цель занятия и выполнить установки на организацию деятельности всех учащихся. По итогам семинара учитель обобщает занятия, отвечает на возникшие вопросы, оценивает деятельность учащихся.
Покажем пример проведения семинара без предварительной лекции по теме «Функции» в Х классе. Ведущей целью такого семинара будет обобщение и расширение знаний о понятии функции.
Так как учащиеся имеют основные знания о понятии функции, то необходимо четко уяснить, что по данной теме будет обобщаться, а что получает расширение и уточнение.
Вводное слово учителя и должно учесть этот момент: 1) функция — частный вид соответствия; 2) область определения и множество ее значений могут находиться различными путями (установление множества значений формулы, пересечения множеств значений); 3) специфика употребляемой терминологии и символов при изучении функций в школе (формулы, задающие функции, могут быть не только алгебраического характера, как это было в примерах функций, изучаемых в восьмилетней школе).
Темы докладов учащихся могут быть следующие:
1. Способ задания функции алгебраической формулой и особенности установления D (f) и Е(f).
2. Тригонометрические функции и их D(f) и Е(f).
3. Функции ![]() и
и ![]() и их D(f) и Е(f).
и их D(f) и Е(f).
4. Функция ![]() и их D(f) и Е(f).
и их D(f) и Е(f).
![]() При консультировании докладчиков можно в
качестве примеров для первого доклада предложить примеры:
При консультировании докладчиков можно в
качестве примеров для первого доклада предложить примеры:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) 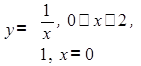
Основной математический материал сообщений учащихся может быть занесен на кодопозитивы, что поможет сэкономить время.
Каждому докладчику необходимо выделить из числа учащихся оппонента, в обязанности которого входит предварительно ознакомиться с материалами сообщения и дать устную рецензию на сообщение (хорошо ли отобран материал для раскрытия темы, как докладчиком был изложен материал: доступно, эмоционально, последовательно, удачно оформлен и т.п.).
В качестве примера, проверяющего
сознательное усвоение темы (1), можно предложить классу найти область
определения функции ![]() (так как
промежутки [
(так как
промежутки [![]() ) и (
) и (![]() ] не пересекаются,
то формула
] не пересекаются,
то формула ![]() не определяет никакой функции).
не определяет никакой функции).
Чтобы учащиеся класса не были пассивными слушателями, а занятие-семинар не свелось к подготовке докладов двумя-тремя учащимися, необходимо дать на дом всем учащимся вопросы для осмысления литературы — основной и дополнительной, задания.
В нашем при мере это может быть:
а) Колмогоров А. Н. Что такое функция // Kвант.- 1970.- № 1, № 2.
б) Виленкин Н. Я. Функции в природе и технике.- М.: Просвещение, 1985;
В качестве проблемы для обсуждения на семинаре может быть следующая: может ли одна и та же функция быть задана несколькими различными формулами и может ли одна и та же формула быть использована для задания нескольких различных функций?
В обобщающей речи учителя можно дать краткую историческую справку развития понятия функции от Г. В. Лейбница до Н. И. Лобачевского и И. Бернулли и очертить необходимый круг сведений по вопросу трактовки понятия функции, важный для учащихся средней школы.
В качестве существенных характеристик материала, который может быть предложен для занятий-семинаров, можно указать следующие:
1) материал обобщающего характера, как в нашем примере с функцией;
2) различные варианты решения «фундаментальных» школьных математических задач (например, задачи о построении сечений многогранников (см. [102])) или «именных» школьных теорем: теоремы Пифагора, о трех перпендикулярах и т.п.;
3) материал, раскрывающий фундаментальные математические понятия, с привлечением исторических справок развития этих понятий в науке и отражение этого развития в школьном курсе (функция, уравнение, вектор и т.п.).
Можно проводить занятие-семинар после школьной лекции. Например, после вводной лекции по теме «Многогранники», приводимой нами выше, возможно провести семинарское занятие, на котором заслушать доклады: 1) о возможных трактовках многогранника (см. [15]); 2) о связях понятий «многоугольники» и «многогранники»; 3) о правильных многоугольниках и многогранниках; 4) о паркетах и др.
Работа по подготовке и организации занятия семинара и в этом случае должна содержать все те основные моменты, которые были отмечены ранее.
Самостоятельная работа
Задание 1. Охарактеризуйте при анализе занятия семинара основные виды самостоятельной работы учащихся на занятиях и сравните их с видами, обычно используемыми на комбинированных уроках математики.
Задание 2. На основе результатов выполнения задания 1 сформулируйте цели проведения посещенного занятия семинара, уделив внимание прогнозированию действий учащихся.
Задание 3. Составьте краткий план занятия-семинара на тему «Различные способы доказательства теоремы о трех перпендикулярах». При составлении плана обратите внимание на четкую формулировку основной познавательной мысли занятия семинара.
Литература: [93], [75], [9], [5], [13].
§ 7. ЛАБОРАТОРНЫЕ РАБОТЫ, РАСКРЫВАЮЩИЕ МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ОБУЧЕНИЯ МАТЕМАТИЧЕСКИМ МЕТОДАМ В ШКОЛЕ
В предлагаемых лабораторных работах рассматриваются функции методов математики, их содержание и место в школьном предмете математики и методические особенности более эффективного использования методов математики в процессе обучения математике.
Прежде чем перейти к непосредственному рассмотрению математических методов, сделаем несколько замечаний о функциях и содержании понятия «метод» в процессе обучения вообще. Для этого надо ответить на следующие вопросы:
1) Что понимается под методом и какие компоненты в нем можно выделить?
2) Почему нужно и важно специально изучать в школе и вузе определенные системы элементов учебного материала на уровне метода?
3) Каким образом следует конкретизировать общее понятие «метод» в случае обращения к методам математики, изучаемым в школе?
Остановимся на каждом из перечисленных вопросов.
1. В теории научного познания метод трактуется как система последовательных действий, которые приводят к достижению результата, соответствующего намеченной цели. Эта последовательность действий может иметь целью как теоретический результат, так и практическую реализацию. Значит, метод выступает в качестве способа познания, способа практической деятельности. Способ познания, способ практической деятельности всегда направлен на определенный объект; поэтому с любым методом обязательно соотносят его объект (познаваемый, преобразуемый).
Таким образом, в методе выделяют две стороны: объективную и субъективную. Первая обращена к гносеологической природе метода и означает, что он (метод) основан на знании сущности и закономерностей познаваемого или преобразуемого объекта, адекватен сущности объекта. Вторая сторона связана с деятельностью по применению метода, с конкретной целью деятельности над изучаемым объектом.
Выделение в методе двух указанных сторон создает условия для решения вопроса о его компонентах. По нашему мнению, ответ на этот вопрос не является однозначным. Он зависит от того, какая из сторон метода в том или ином случае является ведущей. Поэтому можно говорить о компонентах метода, связанных, во-первых, с объективной его стороной (назовем их гносеологическими компонентами); во-вторых, с субъективной стороной (деятельностные компоненты). Совокупность гносеологических и деятельностных компонентов и дает нам представление о компонентах метода в широком смысле.
Что же имеют в виду, говоря о компонентах метода? Рассмотрим этот вопрос с точки зрения гносеологии и с точки зрения деятельности.
Объективная сторона метода, как уже подчеркивалось, связана с проникновением в сущность и закономерности познаваемого, преобразуемого объекта. Необходимым условием этого является определенная система знаний, без которых метод не существует. Такая система должна содержать, во-первых, исходные знания об объекте, к которому применяется метод, его свойствах (основные понятия, свойства понятий, связи между ними); во-вторых, знания, полученные в ходе преобразования или изучения объекта (изменение свойств объекта под влиянием действий над ним, установление неизвестных до этого свойств). Заметим, что указанные знания в определенной мере зависят от предполагаемого результата использования метода, соответствующего поставленной цели. В-третьих, система должна включать знания о сфере приложения метода (круг задач, решаемых с помощью данного метода, их виды и т.д.); в-четвертых, знания об особенностях его использования в зависимости от сферы приложения. Перечисленные компоненты и составляют гносеологическую основу метода.
К деятельностным компонентам метода относятся, с одной стороны, определенная система действий (зависящая от конкретной цели деятельности над изучаемым объектом), реализация которой ведет к достижению результата (соответствующего поставленной цели}, с другой стороны, средства осуществления деятельности, основу которой составляет эта система действий (интеллектуальные, практические, предметные).
2. Обратимся к школьному предмету математики. Как известно, в нем выделяются теоретические знания, которыми должны владеть учащиеся, и задачи, выступающие как средство усвоения теоретических знаний и как специальный объект, цель изучения для формирования подобия математической деятельности. Среди прочих элементов теоретические знания включают методы математики как науки (общий дедуктивный метод математики и частные методы: координатный, векторный, геометрических преобразований, уравнений и неравенств и др.).
Почему же важно усвоение учащимися методов математики и понимание методических особенностей этого усвоения? Ответ на этот вопрос предполагает, по нашему мнению, установление их общеобразовательного, мировоззренческого значения.
С образовательной точки зрения знакомство и овладение методом позволяет учащимся и студентам понять, каким же методом наука математика получает достоверные для нее факты. В одних науках таким методом может быть корректно поставленный эксперимент (например, в физике), в других — правильно организованное наблюдение (например, в биологии). В математике факт получает статус научного (достоверного) только в том случае, если он доказан одним из математических методов. Понимание этой особенности науки математики является необходимым условием ее сознательного изучения.
С общеобразовательной, содержательной точки зрения методы математики выполняют в определенной мере и функцию обобщения, систематизации тех знаний, которые с данным методом так или иначе связаны. Уже имеющиеся знания в результате осмысления их через призму метода «поворачиваются» к учащимся как бы с другой стороны, что может способствовать их углублению, включению в новые связи, отношения и т.п. Кроме того, благодаря изучению методов математики учащиеся получают конкретные приемы решения ряда математических задач.
Мировоззренческое значение методов математики определяется в первую очередь их интегрирующей функцией: с одной стороны, появляется возможность через приложения методов показать проникновение математики в другие науки, в практику; с другой стороны, выделить то общее, что объединяет все методы математики (в определенной мере единый подход в применении, этапы применения методов), а через них — составляющие школьного предмета математики (алгебру, геометрию, элементы математического анализа).
Изучение методов математики важно и в методологическом отношении, ибо представляет возможность для раскрытия содержания понятия «метод» И выделения компонентов метода.
3. В соответствии с перечисленными выше компонентами метода конкретизация общего понятия «метод» при обращении к методу математики, изучаемому в школе, может идти по следующим линиям: уточнение цели метода; установление системы знаний, составляющих гносеологическую основу метода; указание определенной последовательности действий, средств осуществления деятельности, реализация которых приведет к достижению цели.
Но раскрытие только содержания методов математики недостаточно для того, чтобы установить хотя бы некоторые общие положения методики их формирования у учащихся. Следует также определить, формирование каких компонентов конкретного метода должно предшествовать усвоению других, какие средства при этом целесообразно использовать и т.д.
Решение указанной методической задачи связано с теми функциями, которые выполняют методы математики в процессе обучения: с одной стороны, методы математики выступают как цель изучения, а с другой, как средство изучения математического материала (в том числе средство решения задач). Очевидно, что некоторый метод может стать одним из средств изучения математики лишь в том случае, если школьники умеют применить его при решении конкретно-практических задач. А это означает; что в процессе формирования метода математики учитель и учащиеся неизбежно сталкиваются с необходимостью решения, по крайней мере, двух задач (для учащихся это учебные задачи). Первая состоит в том, чтобы школьники овладели содержательной стороной метода, а вторая заключается в обучении применению метода.
Поскольку с любым методом связаны его компоненты, то появляется возможность выделения тех из них, которые в большей мере должны быть «задействованы» в процессе решения двух указанных задач.
По нашему мнению, решение первой задачи предполагает усвоение школьниками деятельностных компонентов метода (соответствующей системы действий) и тех гносеологических компонентов, без опоры на которые не могут быть реализованы деятельностные компоненты. Вторая задача (обучение применению метода) может быть решена при условии, если школьники усвоят гносеологические компоненты метода, связанные с установлением новых свойств исследуемого объекта, видов задач, их особенностей, научатся выбирать метод, который целесообразно использовать при решении конкретной задачи: поэтому обучение методу — это обучение выбору метода.
Заметим, что решение двух указанных задач осуществляется во взаимосвязи и представляет собой достаточно длительный процесс, в котором нельзя четко выделить этапы решения каждой задачи. Результатом этого процесс а должно быть усвоение школьниками методов математики на уровне применения, что предусмотрено программой для средней школы.
Лабораторные работы, посвященные данной теме, показывают, как некоторые общие методы математики реализованы в школьных учебниках математики и как возможно раскрыть их сущность учащимся.
Целесообразность рассмотрения вопроса об обучении учащихся методам математики объясняется, с одной стороны, тем, что методической литературе этот вопрос в достаточно полном объеме практически не освещается; с другой стороны, изучение опыта работы учителей показывает, что они не всегда могут выделить содержание методов математики, изучаемых в школе, а это отрицательно сказывается на выводах о вариантах методики их формирования.
Следует также отметить и методический аспект значения математических методов: обращение к ним способствует формированию ряда методических умений, связанных, например, с целеполаганием и планированием деятельности учителя и деятельности учащихся (в частности, постановка учебной задачи, выделение действий, которыми должны овладеть учащиеся, и др.), переосмыслением имеющихся знаний по математике, методике преподавания математики, их систематизацией и обобщением.
Одна из основных целей обучения математическим методам (и вообще обучения математике в средней школе) состоит в показе возможностей использования математики для решения практических задач, в обучении школьников реализации этих возможностей на производстве, в научной работе, в быту.
Самым существенным компонентом процесса решения практических задач методами математики является математическое моделирование. Поэтому достижение указанной цели должно быть обязательно связано с формированием у учащихся умений строить и исследовать математические модели.
Целенаправленная работа по реализации поставленной цели будет способствовать овладению моделированием не только как методом решения практических задач, но и как методом научного познания, будет решать вопросы формирования у учащихся диалектико-материалистического мировоззрения, понимания значимости абстрактных научных понятий (иначе научных моделей) в познании реальной действительности.
В настоящее время моделирование очень широко при меняется не только в научных исследованиях, но и при решении задач, возникающих в технике, экономике, геологии, медицине и т.д. Поэтому понятия «моделирование» и «модель» рассматривают в широком смысле.
Моделью некоторого объекта А (оригинала) называют объект В, в каком-то отношении подобный (аналогичный) оригиналу А, выбранный или специально построенный человеком для одной (по крайней мере) из следующих целей:
1) заменить оригинал А в мысленном или реальном действии. Такая замена производится тогда, когда для действия в данных условиях объект В более удобен (в этом случае мы имеем дело с моделью-заместителем);
2) создать представление об оригинале А с помощью объекта В (модель-представление);
3) истолковать объект А в виде объекта В (модель-интерпретация);
4) исследовать объект А с помощью объекта В, посредством объекта В (исследовательская модель).
Обычно человек выбирает или строит модель для одной из перечисленных целей, поэтому вид модели именно этой целью и определяется. Но модель может быть использована, как правило, одновременно и для других целей. Например, для решения текстовой задачи строим модель той ситуации, которая в задаче отражена, - уравнение. Это уравнение является исследовательской моделью (оно дает нам возможность установить ряд свойств, характеризующих заданную ситуацию). Но эта модель одновременно служит и моделью-заместителем (в процессе решения задачи она замещает ситуацию), и моделью-представлением (дает нам обобщенное представление о рассматриваемой задаче), и моделью-интерпретацией (уравнение на языке алгебры фиксирует и истолковывает существенные особенности предложенной в задаче ситуации).
Говоря о моделировании, имеют в виду деятельность по построению (или выбору) моделей для указанных выше целей.
Математическая модель — это специальное описание (часто приближенное) некоторой проблемы, ситуации, которое дает возможность в процессе ее анализа применять формально-логический аппарат математики. При математическом моделировании имеем дело с теоретической копией (копия построена нами), которая в математической форме выражает основные закономерности, свойства изучаемого объекта.
В процессе математического моделирования выделяют три этапа:
I. Формализация — перевод предложенной задачи (ситуации) на язык математической теории (построение математической модели задачи).
II. Решение задачи в рамках математической теории (говорят: решение внутри модели).
III. Перевод результата математического решения задачи на тот язык, на котором была сформулирована исходная задача (интерпретация полученного математического решения).
Чаще всего математическая модель представляет собой несколько упрощенную схему (описание) оригинала, а значит, обладает определенным уровнем погрешности.
Одна и та же модель может описывать различные процессы, объекты; поэтому результаты внутримодельного исследования одного явления зачастую могут быть перенесены на другое. В этом состоит одно из основных достоинств математического моделирования.
Как уже указывалось, формировать у учащихся умения, связанные с построением и исследованием моделей (в том числе и математических), необходимо. А для этого нужно говорить об использовании моделирования в обучении, причем речь может идти о различных аспектах такого использования:
первый — моделирование выступает и как содержание, которое должно быть усвоено учащимися в результате обучения, и как способ познания, которым должны овладеть школьники;
второй — моделирование является одним из учебных средств, с помощью которого формируется учебная деятельность учащихся.
Реализация первого аспекта использования моделирования в обучении предполагает:
- формирование у учащихся представлений о модельном характере изучаемых закономерностей, введение в содержание обучения понятий «математическая модель», «моделирование», установление сущности, роли моделирования в познании и т.д.;
- обучение школьников построению моделей, т.е. обучение действию моделирования.
Рассматривая второй аспект использования моделирования в обучении, необходимо подчеркнуть следующее. Моделирование, модели служат средством, с помощью которого происходит познание изучаемых объектов; значит, учащиеся должны уметь строить эти модели и пользоваться ими.
По цели использования в обучении учебное моделирование можно условно разделить на два вида:
- моделирование объектов изучения;
- моделирование действий и операций по изучению этих объектов.
Первый из указанных видов служит для выявления и
фиксации (иногда в наглядно-действенной форме) тех общих отношений, которые
отражают сущность, изучаемых явлений, объектов, процессов. Например, ![]() - теоретическая модель понятия «квадратное
уравнение с одной переменной». Эта модель и ее конкретизации используются как
для изучения теории квадратных уравнений вообще, так и для решения задач практического
содержания.
- теоретическая модель понятия «квадратное
уравнение с одной переменной». Эта модель и ее конкретизации используются как
для изучения теории квадратных уравнений вообще, так и для решения задач практического
содержания.
Второй вид учебного моделирования применяется для выявления и фиксации (чаще в обозримой, наглядной форме) общей схемы действий и операций, связанных с решением определенного круга задач. В учебной модели этого вида показывается, какие действия, операции, в каком порядке (при каких условиях) нужно произвести, чтобы изучить определенный объект данного вида. По сути каждая такая модель — это схема деятельности по решению учебной задачи, связанной с изучением некоторого вида объектов.
Например, любое алгоритмическое предписание выполнения определенного действия есть соответствующая модель, которая выступает в роли учебной, если ставится задача изучения сущности, свойств и т.п. этого действия. А получение предписания, фиксация его — учебное моделирование второго вида.
Можно говорить, что первый вид учебного моделирования отражает предметную сторону учебной деятельности школьников, а второй — оперативную сторону. Так как в реальной учебной деятельности эти две стороны всегда выступают в единстве, то в подавляющем большинстве случаев учебные модели используются и как модели изучаемых объектов, и как модели действия для этого изучения.
Выделим умения, на основе которых школьники смогли бы самостоятельно строить модели, а затем, имея в виду результат работы с моделью и соотнося его с условием предложенной задачи, делать обоснованный вывод о решении исходной задачи. К таким умениям прежде всего следует отнести группы умений, связанных с выявлением, фиксацией тех общих отношений, которые отражают сущность изучаемых объектов, явлений;
записью выявленных отношении на языке той теории, в рамках которой будет решаться задача (с учетом конкретных условий, в которых эти отношения рассматриваются);
переводом полученных в ходе исследования модели результатов на язык, в котором была предложена исходная задача.
Метод математического моделирования находит непосредственное отражение в методах математики, конкретизируется в них.
Лабораторная работа № 14
Тема. Аксиоматический метод доказательства в школьном курсе математики.
Цель. Систематизировать знания и умения по основному методу доказательства в математике: раскрыть его содержание применительно к школьному уровню строгости доказательств и процесс доказательства; проследить этапы и конкретные приемы формирования данного метода в школе.
Оборудование. Таблицы, диафильм «Как устроена теорема» В.Г. Болтянского, кодопозитивы.
Основное содержание
I. Формирование аксиоматического метода
3адание 1. Систематизируйте знания по аксиоматическому методу доказательства математических утверждений.
1. «Аксиоматический метод — способ построения научной теории, при котором в ее основу кладутся некоторые исходные положения (суждения) — аксиомы, или постулаты, из которых все остальные утверждения этой науки (теоремы) должны выводиться чисто логическим путем, посредством доказательств» (БСЭ.- 3-е изд. -1969. - Т. 1. - С. 345).
Так как в традиционной логике одной из форм доказательства было дедуктивное доказательство, т.е. доказательство, когда единичный тезис подводился под общее правило с учетом видов дедуктивного умозаключения и логических правил вывода, то иногда аксиоматический метод называют дедуктивным методом, выделяя тем самым в нем построение доказательств или процесс проведения доказательств.
2. Доказательства «...представляют собой цепочки умозаключений (правильных), ведущих от истинных посылок (исходных для данного доказательства суждений) к доказываемым (заключительным). Истинность посылок не должна обосновываться в доказательстве, а должна каким-либо образом устанавливаться заранее» (БСЭ.-3-е изд.-1977.- Т. 8. - С. 399).
Посредством доказательства удостоверяется истинность или ложность данного суждения.
3. Структура доказательства.
Доказательство включает в себя три основных элемента:
а) Тезис (главная цель доказательства — установить истинность тезиса). Форма выражения тезиса — суждение.
б) Аргументы (основания) доказательства — положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов — суждения. Связывая аргументы, приходим к умозаключениям, которые строятся по определенным правилам. Аргументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы.
в) Демонстрация — логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.
4. Правила доказательства. Они опираются на соответствующие законы.
5. Умозаключение — логическое действие, в результате которого из одного или нескольких известных нам и определенным образом связанных суждений получается новое суждение, в котором содержится новое знание. Существуют различные типы умозаключений:
- индуктивные (процесс рассуждения идет от знания частных фактов к знанию общего правила);
- дедуктивные (рассуждение идет от знания общего правила к знанию о каком-либо единичном, частном факте, на который общее правило распространяется).
6. Под методом доказательства будем понимать способ связи аргументов от условия к заключению суждения. Методы доказательства, используемые в школьном курсе математики, можно выделить по двум основаниям:
- по тому, как строится обоснование тезиса (прямое и косвенное);
- по тому, какой математический аппарат используется для доказательства.
Назовем несколько общих приемов проведения доказательства по первому основанию, т.е. с учетом того, как строится обоснование тезиса.
Прямые приемы поиска доказательства:
а) прием преобразования условия суждения (синтетический);
б) прием преобразования заключения суждения:
- отыскание достаточных оснований справедливости заключения (восходящий анализ);
- отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений (нисходящий анализ);
в) прием последовательного преобразования то условия, то заключения суждения.
Косвенные приемы поиска доказательства:
а) «метод от противного» (истинность доказываемого тезиса устанавливается посредством опровержения противоречащего ему суждения);
б) разделительный (тезис рассматривается как один из возможных вариантов предположений, когда все предположения отвергаются, кроме одного).
Методы доказательства, выделенные по второму основанию, т.е. когда способ связи аргументов согласуется с определенной математической теорией в школьном курсе математики, следующие:
а) метод геометрических преобразований, при реализации которого наряду с логической основой используется аппарат геометрических преобразований;
б) алгебраические методы (уравнений, неравенств, тождественных преобразований);
в) векторный, использующий аппарат векторной алгебры;
г) координатный, позволяющий устанавливать переход от геометрических отношений к аналитическим.
При доказательстве математических утверждений используются разные математические методы. Иногда интересно проверить силу и оригинальность разных методов для доказательства одного и того же утверждения.
3адание 2. Докажите разными методами, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам. равны.
1 способ. Дедуктивный (рис. 16)
Дано: ![]() равнобедренный, АС
— основание, АЕ и СК — медианы.
равнобедренный, АС
— основание, АЕ и СК — медианы.
Доказать: АЕ=СК.
Доказательство. Так как ![]() равнобедренный с основанием АС, то
равнобедренный с основанием АС, то ![]() (по определению равнобедренного
треугольника) и
(по определению равнобедренного
треугольника) и ![]() (по свойству углов при основании
равнобедренного треугольника). Так как CK — медиана, то АВ=2АК (по
определению медианы). Аналогично BC=2CE. Из того, что AB=BC, АВ=2АК,
ВС=2СЕ, следует, что АК=СЕ. В треугольниках АКС и СЕА имеем
АК=CЕ, АС=АС (общая сторона двух треугольников),
(по свойству углов при основании
равнобедренного треугольника). Так как CK — медиана, то АВ=2АК (по
определению медианы). Аналогично BC=2CE. Из того, что AB=BC, АВ=2АК,
ВС=2СЕ, следует, что АК=СЕ. В треугольниках АКС и СЕА имеем
АК=CЕ, АС=АС (общая сторона двух треугольников), ![]() . Эти треугольники равны (по двум сторонам
и углу между ними). Отсюда АЕ=СК (по определению равных треугольников).
. Эти треугольники равны (по двум сторонам
и углу между ними). Отсюда АЕ=СК (по определению равных треугольников).
2 способ. Векторный (рис. 17).
Введем векторы: ![]() . Тогда
. Тогда ![]()

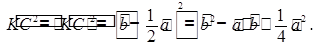
Так как ![]() равнобедренный, то
АВ=ВС, т.е.
равнобедренный, то
АВ=ВС, т.е. ![]()
Следовательно, ![]() тогда
тогда ![]() а значит, АЕ=СK.
а значит, АЕ=СK.
3 способ. Координатный (рис. 18).
Введем систему координат. Ось х проходит по стороне АС, ось у — по высоте, проведенной к основанию. Тогда вершины треугольника будут иметь следующие координаты:
![]()
Так как отрезки АЕ и СК — медианы, то точки К и Е — середины отрезков АВ и СВ. Тогда точки Е и К будут иметь следующие координаты:
![]() . Найдем длины
отрезков АЕ и СК:
. Найдем длины
отрезков АЕ и СК:
![]() ;
;
![]() .
.
Длины отрезков АЕ и СК равны, значит, и сами отрезки равны. Анализируя каждый из способов доказательства, нетрудно выяснить, что в основе каждого из них объективно лежит логическая основа доказательства; поэтому научить понимать дедуктивное доказательство и овладевать приемами его поиска и выполнения есть одна из существенных особенностей обучения курсу математики.
Для того чтобы учащиеся овладели прямым и косвенным доказательствами, необходимо сформировать у них определенную последовательность умений.
Умение доказывать — сложное умение, оно состоит из
умения искать доказательство (анализировать утверждение); получать продуктивные следствия из условия; выяснять условия, при которых возможно заключение; высказывать правдоподобную гипотезу и т.п.;
умения проводить доказательство (на основе полученной гипотезы, возникшей как результат поиска доказательства), выполнять последовательность умозаключений и обосновывать правомерность полученных выводов;
умения оформлять доказательство теоремы.
II. Формирование умений искать доказательство
1. Тенденция построения учебников по геометрии для средней школы в основном ориентирована сейчас на аксиоматическую теорию. Сразу ли в начале курса (как в учебнике [113]) излагаются все аксиомы школьного предмета геометрии или по мере содержательной необходимости в них (как в [44] - [47] или в учебнике [16]), но подход такой стал объективной реальностью. А коль такой подход стал определяющим, то и знакомство с аксиоматическим методом, доказательства методически оправданнее относить к школьному курсу геометрии. Поэтому формирование основных компонентов данного метода осуществляется в основном на учебном материале курса геометрии.
В обучении аксиоматическому методу, как это было отмечено выше можно выделить несколько этапов.
Первый этап направлен на формирование общих приемов поиска и проведения доказательства, которые затем будут использоваться на всех последующих этапах. Этот этап необходимо осуществлять во время изучения первых тем школьного курса геометрии. Данный этап включает в себя следующее:
- анализ текста утверждения;
- развертывание условия;
- последовательный анализ заключения и условия утверждения;
- раскрытие содержания прямого и косвенного методов доказательства.
Второй этап включает освоение специфических приемов поиска и проведения доказательства утверждений в зависимости от конкретного их содержания и собственно математических методов, используемых при доказательстве утверждений.
Третий этап включает в себя раскрытие сущности построения школьного предмета на основе аксиоматической теории.
В построении школьных курсов математики можно выделить три подхода:
- построение курса на содержательной основе, когда материал располагается в систематическом порядке. Причем система эта определяется как принятыми математическими трактовками фундаментальных понятий (число, фигура, функция и т.п.), так и развертыванием последующих определений объектов и доказательством отдельных свойств этих объектов. Система аксиом при таком построении не вводится. Для аргументации используются и ранее доказанные теоремы, и свойства, «прочитанные» на чертеже;
- построение курса основано на дедуктивном подходе, т.е. на определенной аксиоматике, которая вводится постепенно. Степень доказательности утверждений постепенно усиливается;
- построение курса на дедуктивной основе. Система аксиом вводится в начале курса. Раскрывается смысл терминов: аксиома, теорема, доказательство. Оговариваются аргументы доказательства. В начале курса доказательства строятся по возможной для этого возраста учащихся и особенностей школьного предмета строгости с целью раскрытия некоторых положений дедуктивного метода в математике.
Осмыслить третий этап понимания аксиоматического метода можно либо в завершение курса планиметрии, либо при раскрытии логического построения курса стереометрии.
Наиболее существенный и трудный первый этап обучения аксиоматическому методу в школе, поэтому отметим некоторые наиболее важные его особенности.
2. Формирование общих приемов доказательства математических утверждений.
Первый этап в начале изучения курса геометрии может быть реализован в основном на репродуктивно-алгоритмическом уровне. Этот уровень характеризуется умением узнавать ранее изученное доказательство, раскрывать его структуру и воспроизводить чаще всего по тому же рисунку, который приведен в учебнике. Ученик должен уметь воспроизвести доказательство в аналогичной ситуации.
При формировании отдельных общих приемов обучения доказательству математических утверждений необходимо раскрыть его операционный состав, способы формирования операций и критерии сформированности.
1*. Анализ текста утверждения имеет следующий операционный состав:
- прочитайте утверждение;
- выделите условие(я) и заключение(я);
- уточните заключение: назовите его, о каких фигурах идет речь, по какому свойству можно их установить, что в условии есть для того, чтобы получить заключение;
- уточните условие: перечислите фигуры, о которых идет речь, сколько их, какими свойствами они обладают, что в них есть для того, чтобы прийти к заключению;
- сделайте чертеж (если он необходим) и краткую запись;
- если после выполнения анализа доказательство найдено, запишите его.
Чтобы научить учащихся читать математические утверждения. необходимо по казать возможные конструкции утверждении.
Например:
![]()
объект свойства объектов
(объекты) (взаимосвязь между объектами)
3адание 3. Прочитайте всеми приведенными выше способами:
-
Смежные
углы ![]() сумма углов равна 180°.
сумма углов равна 180°.
-
Два
отрицательных числа ![]() сумма чисел есть
число отрицательное.
сумма чисел есть
число отрицательное.
-
Два
числа с разными знаками ![]() произведение чисел
есть число отрицательное.
произведение чисел
есть число отрицательное.
Выражение имеет значение ![]() знаменатель выражения не равен нулю.
знаменатель выражения не равен нулю.
Чтобы выделить условие, ученик должен ответить на вопрос, о чем говорится в утверждении. Для выделения заключения надо ответить на вопрос, что говорится о данном объекте в утверждении. Хорошим средством для формирования умения выделять условие и заключение является составление списков свойств основных (первичных), зафиксированных в определении, и вторичных.
Например:
![]() По мере изучения угла появляются новые
свойства и список значительно расширяется:
По мере изучения угла появляются новые
свойства и список значительно расширяется:
Угол ![]()
3адание 4. а) Выделите, о чем говорится в следующих предложениях и что говорится о выделенном объекте:
- если знаменатель выражения не равен нулю, то данное выражение имеет смысл;
- сумма смежных углов равна 180°;
- вертикальные углы равны.
б) Составьте список свойств следующих объектов: луч, отрезок треугольник.
2*. При формировании приема развертывания условия необходимо раскрыть его операционный состав, который можно представить в виде схемы
Так как большинство умозаключений в школьном курсе математики делается по правилу заключения и правилу отрицания, то на содержательном уровне возможно познакомить с ними учащихся.
а) Если А, то В ![]()
![]() выполняется А.
выполняется А.
Вывод: выполняется В;
б) Если А, то В ![]()
![]() не выполняется В.
не выполняется В.
Вывод: не выполняется А.
3адание 5. а) Известно, что точки А и К лежат в разных полуплоскостях относительно данной прямой. Какие выводы можно сделать из этого условия?
б) Известно, что выполняется равенство ![]() Как расположены точки М, Р и К?
Какие еще утверждения можно доказать, имея данное условие?
Как расположены точки М, Р и К?
Какие еще утверждения можно доказать, имея данное условие?
в) По данному чертежу сформулируйте утверждение, которое можно доказать.
3адание
6.
Используя прием развертывания условия, осуществите доказательство утверждения.
Если прямая, не проходящая ни через одну из вершин треугольника, пересекает
одну из сторон треугольника, то она пересекает только одну из двух других
сторон треугольника.
3*. При формировании приема последовательного анализа заключения и условия утверждения операционный состав его может быть раскрыт в схеме
Для формирования умения находить достаточные основания можно использовать, например, следующие задачи:
1) Даны две полупрямые. Что должно быть известно, чтобы можно было утверждать, что дан угол? что дан развернутый угол?
2) Что достаточно знать для того, чтобы утверждать, что данный треугольник равнобедренный?
3) Известно, что выполняются следующие равенства: АВ=МР,
ВС=РК. Дополните это условие так, чтобы можно было сделать вывод, что ![]() .
.
4) Найдите условия, недостающие в тексте задачи, для того, чтобы можно было прийти к заключению:
а) Дано: α и β — углы.
?
Доказать: ![]()
б) Дано: a, b и c — прямые,
![]() . ?
. ?
Доказать: ![]()
Хорошим средством для решения приведенных задач является составление карточек вида
|
Для того чтобы доказать |
достаточно доказать |
|
равенство треугольников |
1) равенство двух пар соответственных сторон и равенство углов между ними; 2) равенство трех пар соответственных сторон; 3) и т.д. |
Задание 7. Составьте карточку достаточных условий:
- что данный треугольник равнобедренный;
- что данные прямые параллельные.
Задание 8. Раскройте в виде схемы прием развертывания условия и заключения на примере следующей задачи: в треугольнике проведены две биссектрисы. Докажите, что если их отрезки от точки пересечения до вершин равны, то этот треугольник равнобедренный.
4*. Содержание прямого метода умозаключения раскрыто в ранее приведенных общих приемах поиска доказательства утверждений.
Раскроем операционный состав косвенного метода:
- делаем предположение (строим отрицание того, что требуется доказать);
- рассматриваем вместе условие утверждения и предположение и делаем вывод;
- ищем противоречие с известным истинным утверждением (аксиомой, ранее доказанной теоремой, условием утверждения);
- найдя противоречие, делаем вывод, что наше предположение неверно, а верно его отрицание, т.е. то, что требуется доказать.
Для формирования всех операций приема необходимо показать, что такое противоречие и как строится отрицание.
Задание 9. а) Выясните, могут ли быть одновременно истинными или ложными следующие высказывания:
2+11=13 и 2+11≠13.
Прямые а и b пересекаются и Прямые а и b не пересекаются.
б) Постройте отрицания следующих высказываний:
Числовое значение данного выражения равно 5.
Число 586 делится на 3.
Велосипедист не имеет права ехать на красный и желтый свет.
в) Установите, какие из предложенных утверждений в следующих парах являются отрицаниями друг друга:
x=5; х≠5.
Он мой друг. Он мой враг.
Он мой друг. Он друг моего врага.
![]() остроугольный;
остроугольный; ![]() тупоугольный.
тупоугольный.
![]()
Хорошим условием, позволяющим говорить о сформированности метода, является решение логических задач.
Второй этап формирования аксиоматического метода осуществляется на протяжении изучения всего курса математики.
Задание 10. Выберите учебный материал учебника, на котором более эффективно можно раскрыть содержание первого этапа обучения аксиоматическому методу. Дайте педагогические обоснования вашего выбора (доступность, логическая возможность достижения цели).
Задание 11. Посетите школу и в беседе с учителем (желательно опытным) выясните наиболее характерные затруднения учащихся, возникающие при изучении аксиоматического метода на всех трех этапах его формирования. В соответствии с этим предложите свои варианты формирования данного метода в школе.
Задание 12. Разработайте формы контроля сформированности этапов изучения метода, наиболее характерных приемов и их операционных составов. Предложите реальные задачи и задания к ним, по выполнению которых можно судить о сформированности отдельных приемов и их операций.
Задание 13. Разработайте различные формы записи доказательства математических утверждений с разной степенью обоснованности проводимых доказательств.
Задание 14. Разработайте итоговую лекцию по третьему этапу формирования аксиоматического метода в школе.
Итоговое задание. Напишите реферат на тему «Аксиоматический метод в школьном курсе математики и возможные методики его формирования».
Литература к написанию реферата:
Лабораторная работа № 15
Тема. Метод уравнений и неравенств в курсе математики средней школы.
Цель. Установить связь между методом математического моделирования и методом уравнений и неравенств, выделить этапы формирования метода уравнений и неравенств в курсе математики средней школы.
Оборудование. Набор моделей изучаемых объектов, набор кодопозитивов: этапы математического моделирования; примеры учебных моделей действий, операций; примеры схем, графических интерпретаций, которые могут быть использованы на этапе составления решающей модели задачи.
Основное содержание
Метод уравнений и неравенств — метод математики, в котором наиболее выпукло и ярко отражаются характерные черты, находят четкую реализацию этапы процесса математического моделирования. Этот метод можно считать конкретизацией метода моделирования и с точки зрения тех основных действий, которые характеризуют метод моделирования и которые необходимо выполнять в процессе использования этого метода для решения конкретных практических задач.
Какие вопросы следует осветить в связи с обучением методу уравнений и неравенств? Выделим основные:
- цели изучения метода уравнений и неравенств;
- суть и содержание метода;
- возможности формирования метода в курсе математики средней школы;
- этапы формирования метода;
- задачи, стоящие перед учителем и учащимися.
1*. Так как уравнения, неравенства, их конструкции являются математическими моделями очень многих явлений (физических, химических и др.), то решение различных задач (в том числе и тех, с которыми мы сталкиваемся на практике) в конечном счете сводится к решению уравнений, неравенств, их конструкций. Поэтому цели указанного метода состоят в познании явлении, процессов действительности и в получении способа (часто наиболее рационального, особенно если учесть возможности современных ЭВМ) решения многих практических и научных задач.
Указанные цели метода уравнений и неравенств являются и целями его изучения. Но помимо их можно говорить и о других, которые имеют как образовательное, мировоззренческое, так и дидактическое значение.
Наиболее значимая среди них состоит в возможности формирования у учащихся умения математизации реальных ситуаций, а это, как указывалось выше, связано с формированием такого важного действия, как действие моделирования. Изучение метода уравнении и неравенств в определенной мере преследует цель установления межпредметных и внутрипредметных связей, а значит, формирования системности знаний. Кроме того, создаются благоприятные условия для обобщения и систематизации знаний, связанных с рядом тем курсов алгебры и геометрии (равносильность уравнений, неравенств; способы решения уравнений, неравенств, их систем; описание уравнением, неравенством, конструкцией уравнений, неравенств заданного множества точек и др.).
Задание 1. Приведите примеры, иллюстрирующие положение о том что изучение метода уравнений и неравенств способствует установлению: а) межпредметных связей (например, с курсами физики, химии, географии); б) внутрипредметных связей.
Задание 2. Продумайте возможности систематизации знании при изучении темы «Тригонометрические уравнения». По каким направлениям может осуществляться систематизация знании учащихся?
2*. Суть, основная идея метода уравнений и неравенств заключается в
установлении основных связей, зависимостей между элементами, характеризующими изучаемое явление (процесс), т.е. в построении словесной модели явления (процесса);
переводе словесной модели на язык математики: выявленные связи, зависимости между характеристиками явления записываются в виде уравнений, неравенств или их конструкций. В данном случае имеем дело с построением математической (иногда ее называют решающей) модели;
решении поставленной задачи внутри математической модели: решение уравнения, неравенства или их конструкции (аналитический, графический способы);
переводе полученного результата на тот язык, на котором была сформулирована исходная задача (имеется в виду установление соответствия полученного результата исходному явлению, процессу).
Раскрытие сущности метода уравнений и неравенств фактически связано с выделением этапов деятельности человека, его применяющего (сравнить с этапами процесса математического моделирования).
При изучении курса математики средней школы учащиеся, как правило, не сталкиваются с необходимостью осуществления деятельности, соответствующей первому этапу (в учебниках и различного рода пособиях обычно уже представлены словесные модели исследуемых явлений). Поэтому в дальнейшем, раскрывая содержание метода уравнений и неравенств, не будем учитывать этап построения словесной модели.
Задание 3. Задайте практическую ситуацию (задачу), для решения которой требуется построить ее словесную модель. Какие величины и их значения, необходимые для получения словесной модели, потребовалось выделить?
Перечислим деятельностные компоненты метода уравнений и неравенств:
- выбор и обозначение одного или нескольких основных неизвестных;
- введение обозначений для других неизвестных с учетом:
а) связей и зависимостей, зафиксированных в словесной модели исследуемой ситуации; б) обозначений основных неизвестных;
- составление решающей модели (уравнения, неравенства или конструкции уравнений, неравенств);
- решение полученной модели;
- исследование результата (решения уравнения, неравенства и т.п.) в соответствии с условием поставленной задачи.
Деятельность, основу которой составляют указанные действия, осуществляется, как правило, с помощью интеллектуальных средств; реже используются предметные (например, схемы, графические интерпретации и т.п.).
Задание 4. Укажите те интеллектуальные средства, которые используются при выполнении действий, являющихся компонентами метода уравнений и неравенств. Охарактеризуйте особенности использования этих средств.
Задание 5. Проиллюстрируйте возможности использования предметных средств в деятельности, реализующей метод уравнений и неравенств (приведите конкретные примеры).
Задание 6. Соотнесите действия, входящие в метод уравнений и неравенств, с этапами деятельности по применению этого метода для решения задач.
Содержание гносеологических компонентов метода уравнений и неравенств определяется следующим образом:
1) Знание основных зависимостей между величинами, которые присутствуют в описании явления, процесса, выступающего в качестве объекта применения метода (например, зависимости между путем, временем, скоростью; объемом работы, временем, производительностью труда; стоимостью, ценой, количеством продукции и т.п.), и способов их математического выражения.
2) Результат исследования явления, процесса, который характеризует одну или несколько величин, находящихся в определенной зависимости; следствия из этого результата.
3) В круге задач, решаемых данным методом, выделим типы по признаку «тип решающей модели»: задачи на составление уравнений, задачи на составление неравенств, задачи на составление систем уравнений, задачи на составление систем неравенств, задачи на составление систем уравнения (уравнений) и неравенства (неравенств). Каждый из указанных типов может быть разделен на виды в соответствии, например, с видом решающей модели (задачи на составление линейных, квадратных, дробно-рациональных уравнений и т.д.).
Среди всех видов задач особо отметим задачи на оптимизацию, а среди них — задачи на нахождение: а) наибольшего или наименьшего значения функции, непрерывной на отрезке и имеющей на этом отрезке конечное число критических точек; б) наибольшего или наименьшего значения линейной функции в некоторой области, заданной системой линейных неравенств и линейных уравнений (задача линейного программирования). Указанные задачи относятся к типу «Задачи на составление системы уравнений и неравенств», первая из них рассматривается в курсе алгебры и начал анализа X-XI классов.
Решение каждой из этих задач связано с получением уравнения, задающего некоторую функцию (на отрезке в первом случае и на подмножестве точек координатной плоскости во втором).
4) Особенности использования метода в зависимости от сферы его приложения связаны с необходимостью рационального выбора вида решающей модели предложенной -задачи и проявляются в действиях по применению метода уравнений и неравенств.
Это и рациональный выбор неизвестного, и особенности построения решающей модели (например, получение уравнения, задающего некоторую функцию, и использование производной для нахождения ее критических точек), и особенности решения отдельных видов уравнений, неравенств, конструкций уравнений и неравенств, в частности применение аналитического и графического способов решения, и особенности интерпретации полученного результата в соответствии, с одной стороны, с видом решающей модели, а с другой — с условием конкретной задачи.
Наиболее ярко особенности использования метода уравнений и неравенств проявляются в процессе решения задач геометрического, физического и т.п. содержания, так как выбор вида решающей модели бывает связан с предварительным установлением и использованием «чисто» геометрических, физических и т.п. свойств рассматриваемых объектов, явлений.
Задание 7. В чем достоинства и недостатки деления задач, решаемых методом уравнений и неравенств, на типы по признаку «тип решающей модели»?
Можно ли предложить другую типологию? В чем ее достоинства, недостатки?
Задание 8. Приведите пример конкретной задачи линейного программирования. Выделите этапы ее решения, укажите действия, которые должен выполнить ученик на каждом этапе. Отметьте те особенности, которые характеризуют рассматриваемый вид задач и данную задачу в частности.
При выполнении задания можно обратиться к следующим публикациям:
Малкова Т.В., Монахов В.М. Математическое моделирование — необходимый компонент современной подготовки школьников // Математика в шк.- 1984.- № 3.- С. 46-49.
Рейтман М.И. Транспортная задача // Квант.- 1974.-№ 7.- С. 13-20.
Задание 9. Подберите задачу, которая допускала бы построение различных решающих моделей в зависимости от выбора неизвестного.
Какую модель и почему целесообразно (или возможно) рассматривать на определенном этапе (этап специально оговорить) изучения школьниками курса математики средней школы? Каким образом может быть обоснован учащимся выбор этой модели?
3*. Чтобы установить возможности для формирования метода уравнений и неравенств в курсе математики средней школы, нужно установить, во-первых, те знания и умения, которые являются базовыми по отношению к деятельностными гносеологическим компонентам метода; во-вторых, место и содержание, материала, связанного с методом, в учебниках математики; в-третьих, возможности этого материала с точки зрения формирования отдельных компонентов метода.
Для успешного применения метода уравнений и неравенств учащимся необходимы следующие знания и умения:
- знания об уравнениях, неравенствах, их конструкциях: понятия (уравнения, неравенства и т.д.; корня, решения уравнения, неравенства, системы уравнений, неравенств; равносильности уравнений, неравенств и т.д.; графика уравнения, неравенства); свойства числовых равенств, неравенств; виды уравнений, неравенств; способы решения уравнений, неравенств, их конструкций (аналитический, графический);
- знания зависимостей между основными величинами, свойств геометрических и других объектов, изучаемых в курсе математики средней школы, способов математического выражения этих зависимостей, свойств;
- умения, связанные с решением отдельных видов уравнений, неравенств, их конструкций: получение уравнения, неравенства и т.д., равносильных исходному, с помощью основных теорем равносильности уравнений, неравенств на базе использования свойств функций и т.п.; выбор рационального для каждого конкретного случая способа решения (в том числе аналитического или графического); построение множества точек по его аналитическому заданию; описание уравнением, неравенством и т.п. заданного множества и др.;
- умение осуществлять перевод задачи с языка словесной модели на язык математической модели (т.е. составлять уравнение, неравенство и т.п. В соответствии с указанными в условии задачи свойствами, зависимостями величин);
- умение интерпретировать результат решения математической модели в соответствии с условием предложенной задачи и др.
3адание 10. Познакомьтесь с материалом, связанным с методом уравнений, в следующих школьных учебниках математики: [2З], [24], [З9], [40]. С какими понятиями знакомятся учащиеся, вводятся ли определения этих понятий? Какого вида уравнения решаются в V классе, в VI классе? Какие способы при этом используют учащиеся? Предлагаются ли задачи, решение которых связано с составлением уравнения? Можно ли утверждать, что в этих классах проводится целенаправленная, систематическая работа по формированию метода уравнений?
3адание 11. Ориентируясь на учебники алгебры для VII класса [3], [7], [107], установите, какие виды уравнений, неравенств, их конструкций изучают учащиеся, каковы способы их решения (особое внимание обратите на связь вопросов, связанных с темами «Уравнения» и «Функция»).
Можно ли утверждать, что в курсе алгебры VII класса метод уравнений становится предметом специального рассмотрения? Если да, то в чем это конкретно проявляется? Какие виды задач учащиеся решают методом уравнений (ориентируйтесь на вид решающей модели)?
3адание 12. При изучении какого вида уравнений в курсе алгебры восьмилетней школы впервые появляется необходимость обязательной реализации этапа интерпретации результата решения математической модели в соответствии с условиями поставленной задачи?
Приведите пример задачи, в процессе решения которой методом уравнений мы обязаны обратить внимание учащихся на этап интерпретации. Как методически правильно организовать деятельность учащихся на этом этапе реализации метода уравнений?
3адание 1З. В каком классе и при изучении материала какой темы учащиеся знакомятся с элементами метода неравенств, с какими именно элементами (понятия, их свойства, способы действий с ними)?
Рассматриваются ли задачи, решающей моделью которых являются неравенства, системы неравенств? Приведите примеры.
Обращается ли специальное внимание на особенности использования метода неравенств при решении практических задач?
3адание 14. Проанализируйте учебники алгебры [4], [5], [8], [9] и установите виды уравнений, неравенств, систем уравнений, неравенств, способы их решения, с которыми знакомятся учащиеся.
Какие предлагаются новые виды задач, входящие в компоненты метода уравнений и неравенств? Обращается ли в процессе работы с ними специальное внимание на особенности применения метода уравнений и неравенств?
3адание 15. Имея в виду выполненный анализ материала школьных учебников, сопоставив результаты этого анализа с компонентами метода уравнений и неравенств, а также с теми знаниями и умениями, которые лежат в основе его использования, ответьте на вопросы:
1) Имеются ли в школьном курсе математики возможности для формирования не только отдельных компонентов, но и метода в целом?
2) Реализованы ли эти возможности, формируется ли метод уравнений и неравенств (в принятой нами трактовке) у выпускников средней школы?
4*. Реализация возможностей усвоения школьниками метода уравнений и неравенств связана с решением двух задач. Первая состоит в том, чтобы добиться понимания учащимися сути метода и овладения действиями по его применению (деятельностные компоненты). Вторая задача заключается в обучении применению метода для решения различных видов задач (в процессе ее решения происходит и дальнейшее усвоение деятельностных компонентов, и раскрытие объективной стороны, гносеологической основы метода).
Обе эти задачи должны стать целью деятельности не только учителя, но и учащихся. Их решение предполагает обязательное выделение в процессе формирования метода уравнений и неравенств следующих этапов:
I. Этап принятия учащимися поставленной учебной задачи. Основная цель этого этапа состоит в том, чтобы показать учащимся значение метода уравнений и неравенств и «выйти» на понимание школьниками цели последующей деятельности — усвоение специального метода решения многих задач (в том числе и задач практического содержания).
Основным средством, которое учитель использует на этом этапе, могут быть задачи, причем такие, в процессе решения которых наиболее ярко будет проявляться целесообразность использования именно рассматриваемого метода.
II. Этап усвоения школьниками сути метода. На этом этапе учащиеся под руководством учителя выделяют действия, определяющие операционный состав метода уравнений и неравенств; устанавливают их последовательность; отмечают, что нужно знать и уметь для того, чтобы применять метод.
III. Этап формирования компонентов метода уравнений и неравенств. Используя в качестве основного средства задачи, на этом этапе учитель должен обратить внимание в первую очередь на формирование у учащихся таких действий, как выбор и обозначение одного или нескольких основных неизвестных, введение обозначений для других неизвестных и интерпретация результата в соответствии с условием поставленной задачи.
В действии «составление решающей модели» следует выделить операцию, связанную с выделением основного отношения данной задачи, которое и используется в конечном счете для получения уравнения (неравенства и т.п.).
Замечание. Здесь не указывается на необходимость формирования действия «решение полученной модели», так как оно специально формируется в процессе изучения определенных видов уравнений, неравенств, их систем.
IV. Этап обучения школьников применению метода для решения задач определенного вида. Этот этап основной своей целью имеет формирование у учащихся умений, связанных не с реализацией отдельных компонентов метода, а с применением метода в целом (при этом вид задачи, а значит, и вид решающей модели определен однозначно).
V. Этап обучения школьников применению метода для решения широкого круга математических задач. Основная цель этого этапа формирование у учащихся умения осуществлять рациональный выбор вида решающей модели предложенной задачи.
Выделение в процессе формирования метода уравнений и неравенств перечисленных этапов дает возможность утверждать, что формирование деятельностных компонентов метода (решение первой учебной задачи) в большей мере осуществляется на первом — четвертом этапах, а гносеологических компонентов — на четвертом — пятом этапах. Следует иметь в виду, что предложенное членение анализируемого процесса условно, так как отделить решение одной учебной задачи от другой невозможно. В противном случае не сможем говорить о формировании всех компонентов, а значит, и метода уравнений и неравенств в целом.
Задание 16. Имея в виду курс алгебры (или геометрии) VII класса, подберите две задачи практического содержания, работа над решением которых убедит учащихся в целесообразности специального изучения метода уравнений как метода решения задач (решающие модели задач: линейное уравнение с одной переменной: система двух линейных уравнений с двумя переменными).
Задание 17. Опишите методику организации учителем этапа усвоения школьниками сути метода уравнений и неравенств (на примере задачи, решающей моделью которой будет система линейных неравенств с одной переменной).
Задание 18. Составьте наборы задач, направленных на формирование у учащихся операций:
- введения обозначений для неизвестных, если основное неизвестное установлено;
- выделения основного отношения данной задачи, использующегося для получения уравнения.
Ориентируйтесь на курс математики V-VI классов.
Задание 19. Опишите методику формирования умения применять метод уравнений и неравенств при решении задач определенного вида.
Сделайте это на примере задачи: в 5 л раствора, содержащего 30% кислоты, начали вливать раствор, содержащий 70% кислоты. Сколько нужно влить второго раствора в первый, чтобы их смесь содержала не менее 60% кислоты?
3адание 20. Ориентируясь на курс математики IX класса составьте набор задач, который можно использовать с целью формирования у учащихся умений осуществлять рациональный выбор вида решающей модели предложенной задачи.
Самостоятельная работа
1. Укажите конкретные особенности, связанные с применением метода уравнений и неравенств к решению следующих задач.
Задача 1. Основания трапеции относятся как 2:3, а средняя линия трапеции равна 5 м. Найти основания.
Задача 2. Средняя линия трапеции равна 7 см, а одно из основании больше другого на 4 см. Найти основания трапеции.
Задача 3. Лодка находится на расстоянии 3 км от ближайшей точки А берега озера. Пассажир лодки хочет попасть в село В, находящееся на берегу на расстоянии 5 км от А. Лодка движется со скоростью 4 км/ч, а пассажир, выйдя из лодки, может в час пройти 5 км. К какому пункту берега должна пристать лодка, чтобы пассажир достиг села в кратчайшее время?
Какими знаниями, умениями должны владеть учащиеся, чтобы использовать метод уравнений и неравенств при решении каждой из этих задач?
2. Составьте конспект урока по теме «Системы двух линейных уравнений с двумя переменными. Решение задач».
3. Составьте итоговую контрольную работу по теме «Квадратные уравнения», включив в нее задачу, для решения которой потребуется применить метод уравнений.
Предложите нормы оценки этой контрольной работы, указав конкретно, правильность выполнения каких действий учащихся и каким образом будет оцениваться.
4. Имея в виду конкретную задачу (набор задач), разработайте средства наглядности (например, набор кодопозитивов), которые целесообразно использовать в процессе обучения школьников реализации каждого из этапов процесса математического моделирования при решении задач методом уравнений и неравенств.
Литература: [2], [3], [4], [5], [8], [9], [95], [39], [40], [23], [24], [107], [108], [96], с. 91-122.
Лабораторная работа № 16
Тема. Методика формирования и использования координатного метода в школе.
Цели и учебные задачи. 1. Определить цели и учебные задачи введения и использования координатного метода в школе.
2. Систематизировать понятийный аппарат и основное содержание знаний по координатному методу применительно к школе.
3. Раскрыть специфику использования координатного метода в школьных курсах алгебры и геометрии.
4. Проанализировать школьные учебники по вопросам формирования и использования координатного метода в школе.
5. Разработать конкретную методику формирования отдельных компонентов метода и использования координатного метода в школе.
Оборудование. Учебники, диафильмы «Координатная прямая», «Координатная плоскость», координатная доска, магнитная доска.
I. Цели и учебные задачи изучения координатного метода в школе:
1. Показать, что координатный метод имеет свой язык, свои приемы, используя которые можно выражать свойства геометрических фигур на аналитическом языке в виде уравнений и неравенств и уравнения, функции, неравенства переводить на геометрический язык (графиков).
2. Сформировать понятийный аппарат координатного метода (координатная прямая и координатная плоскость, координаты точки, уравнение прямой, окружности, параболы, гиперболы, уравнение отрезка, координаты середины отрезка).
3. Сформировать конкретные приемы использования координатного метода при изучении курсов алгебры и геометрии.
II. Понятийный аппарат координатного метода для прямоугольной системы координат:
1. Абсцисса (лат. «отсекать») - отрезок, отсекаемый на оси иксов.
2. Ордината (лат. «упорядоченный») - первоначально была только одна ось и ординаты были отрезки, параллельные друг другу, т.е. (рис. 19) в каждой абсциссе строился свой перпендикуляр, если система координат была прямоугольная.
3. Координаты (точки) - числа, взятые в определенном порядке и характеризующие положение точки на линии, на плоскости, в пространстве (КОО совместное).
4. Прямая, на которой указан способ изображения действительных чисел, называется координатной.
3амечание 1. В математике есть теорема (аксиома), вводящая координатную прямую или координаты на прямой. В школе координатная прямая вводится постепенным «присвоением» точкам прямой определенных чисел в связи с расширением числовых множеств и осмыслением операции откладывания отрезка (измерения отрезка).
5. Координатная плоскость — плоскость, на которой
рассматривается два семейства несамопересекающихся линий, таких, что каждая
линия одного семейства пересекается с каждой линией другого семейства только в
одной точке. Начальные линии выбрали x=0 и у=0 (их назвали
осями координат). Линии ![]() и
и ![]() координатные линии.
координатные линии.
6. Координатный метод — способ определения положения точки (на прямой, на плоскости, в пространстве) с помощью чисел (для декартовой системы координат). Используя координатный метод, алгебраические уравнения можно истолковать в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул (уравнений и их систем).
III. Основные знания и учебные задачи, формирующие координатный метод:
- знать запись точки в координатной форме и по данной координатной форме строить ее на координатной плоскости (прямой).
А (x; y) и А(х) — координатные
формы задания точки на плоскости и на прямой.
Геометрическое изображение точки, заданной своими координатами на плоскости и на прямой, показано на рисунках 20 и 21;
- знать задание прямой в координатной форме и по данной координатной форме строить прямую на координатной плоскости.
Прямая однозначно определяется уравнением, если: а) ему удовлетворяют координаты (х; у) любой точки этой прямой, и наоборот; б) любая пара чисел (х; у), удовлетворяющая уравнению прямой, представляет собой координаты соответствующей точки прямой. Любая прямая на координатной плоскости имеет уравнение вида ах+bу+с=0 (или принятое для школьного курса алгебры y=kx+b). Найдя координаты двух точек (рис. 22), можно получить геометрический образ прямой на координатной плоскости. Используя аналитический и геометрический языки, можно описать свойства прямой на аналитическом и геометрическом языках (см. задание для самостоятельной работы).
Аналогично уравнение окружности с центром C (а; b) и
радиусом r будет ![]() (если центр
окружности в начале координат, то уравнение окружности
(если центр
окружности в начале координат, то уравнение окружности ![]() ); уравнение параболы
); уравнение параболы ![]() (путем сдвигов осей координат можно
перейти и к уравнению вида
(путем сдвигов осей координат можно
перейти и к уравнению вида ![]() ).
).
В аналитической геометрии канонический вид гиперболы ![]() если
если ![]() , то гипербола
равнобочная и ее уравнение
, то гипербола
равнобочная и ее уравнение ![]() . Если за оси
координат принять асимптоты равнобочной гиперболы, то уравнение будет
. Если за оси
координат принять асимптоты равнобочной гиперболы, то уравнение будет ![]() или, полагая
или, полагая ![]() получим школьное уравнение гиперболы
получим школьное уравнение гиперболы ![]()
Замечание 2. Необходимо помнить основное требование к уравнению любой линии. Уравнение будет уравнением линии, если ему удовлетворяют координаты (х; у) любой точки этой линии, и наоборот: любая пара чисел (х; у), удовлетворяющая уравнению линии, представляет собой координаты точки.
Данное обстоятельство в школьных математических задачах выражается в заданиях: а) выяснить, принадлежит ли данная точка линии (прямой, параболе, окружности, гиперболе), и б) дана точка на линии, уравнение которой известно, найти ее координаты.
Знание уравнений основных линий, изучаемых в школьном курсе геометрии, сводится к решению двух учебных задач: а) по заданным геометрическим свойствам линии составить ее уравнение; б) по заданному уравнению линии выяснить ее геометрические свойства. В курсе алгебры вторая задача выражается иначе: по заданному уравнению построить график (изобразить график) линии и с помощью графического языка выяснить свойства функции, а затем по возможности выясненные свойства перевести на аналитический язык. Первая задача решается в случае применения координатного метода в геометрии и обычно называется «составление уравнения линии».
В школьном курсе математики используется еще одна группа фактов из аналитической геометрии:
- расстояние между точками;
- деление отрезков в данном отношении (частный случай — нахождение координат середины отрезка).
Данная группа фактов в основном применяется в геометрии для нахождения расстояния между точками и координат середины отрезка.
Задание 1. 1) Выражение «точка принадлежит прямой (кривой}» осмыслите в терминах координатного метода.
2) Как соотносятся с геометрическим образом координаты, задаваемые одним числом?
3) Найдите периметр
треугольника АBC, если А (-7; -3), В (3; -7), C (5; -2).
Докажите, что ![]() прямоугольный.
прямоугольный.
4) Что такое уравнение фигуры в декартовых координатах?
5) Найдите
геометрическое место точек декартовой системы координат, для которых ![]() .
.
6) Составьте уравнение линии, точки которой равноудалены от двух данных точек (0; 1), (1; 2).
IV. Обоснование целесообразности использования координатного метода в школе и основные его этапы.
В качестве примера, способствующего достижению поставленной цели, рассмотрим две математические задачи.
Задача 1. Дана прямоугольная трапеция с основаниями а и b.
Найти расстояние между серединами ее диагоналей.
Дано: ![]() .
.
Найти: ![]()
Сущность
использования координатного метода сводится к нескольким наиболее существенным
действиям: а) написанию (составлению) уравнения линии (прямой, окружности,
параболы и др.); б) нахождению расстояния между точками (написанию уравнения
отрезка), нахождению координат точек на отрезке (чаще середины отрезка; иногда
точки, делящей отрезок в данном отношении).
Этапы использования координатного метода при решении задач геометрии (на материале конкретной математической задачи) следующие:
I этап. Разместить фигуры на координатной плоскости так, чтобы более рационально можно было выразить в координатной форме отрезки фигуры (как данные, так и искомые) и «увидеть» использование координатного метода для нахождения искомого элемента.
У нас это длина отрезка ![]() Чтобы определить
длину
Чтобы определить
длину ![]() , надо найти координаты точек О и
, надо найти координаты точек О и ![]() , а они — середины диагоналей. Значит, надо
иметь координаты концов диагоналей, т.е. вершин трапеции. В нашем примере лучше
прямой угол трапеции совместить с прямым углом системы координат.
, а они — середины диагоналей. Значит, надо
иметь координаты концов диагоналей, т.е. вершин трапеции. В нашем примере лучше
прямой угол трапеции совместить с прямым углом системы координат.
II этап. Записать в координатной форме с учетом данных задачи точки вершины трапеции: А (0; 0), В (0; у), С (b; у), D (а; 0).
III этап. Записать исходя из плана решения задачи уравнение линий, расстояние между точками, координаты середин отрезка и т.п.
В нашем примере надо записать координаты середин отрезка АС и BD:
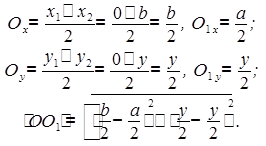
IV этап. Выполнить преобразование полученного в координатной форме выражения
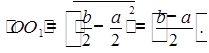
V этап. Осмыслить полученные результаты на том языке, на котором была написана задача.
Так как длина отрезка не может быть меньше 0, то это
возможно только в случае ![]()
Вывод: если ![]() , то
, то ![]()
![]() В решении задачи использовались этапы
моделирования: перевод на другой язык (координатный); работа над выражением в
координатной
форме; перевод с координатного языка на геометрический, осмысление результатов
на этом языке.
В решении задачи использовались этапы
моделирования: перевод на другой язык (координатный); работа над выражением в
координатной
форме; перевод с координатного языка на геометрический, осмысление результатов
на этом языке.
Задача 2. Решить систему
уравнений![]()
Попытка решить уравнение аналитическим путем при водит
к уравнению ![]() которое
элементарными приемами решить невозможно. Для нахождения пар решений данной
системы можно воспользоваться тоже координатным методом, только в ином порядке.
которое
элементарными приемами решить невозможно. Для нахождения пар решений данной
системы можно воспользоваться тоже координатным методом, только в ином порядке.
I этап. Изображаем графики данных в системе уравнении и обозначаем точки пересечения графиков. Координаты этих точек и есть. пары решений данной системы.
Задание 2. Обоснуйте данный вывод.
II этап. Графическим методом находим координаты точек пересечения графиков уравнений и получаем решение системы уравнений.
Задание 3. дайте методическое обоснование преимуществ применения координатного метода для объяснения смысла решения системы уравнений на примере модификации этой задачи.
Задача 3. Сколько решений имеет каждая из систем:
V. Анализ
школьных учебников по вопросам формирования и применения координатного метода в
восьмилетней школе.
Для того чтобы осуществить анализ, выделим: а) основные знания и умения, необходимые для того, чтобы можно было утверждать, что метод сформирован; б) задания, показывающие, что метод применяется осознанно.
К числу знаний. и умений, говорящих о том, что понятийный аппарат метода усвоен, необходимо отнести: 1) понимание двух основных задач метода (построение точки по ее координатам и нахождение координат заданной точки на луче, прямой и плоскости); 2) знание формул, наиболее часто встречающихся в школе фигур (прямой, параболы, гиперболы, окружности) и приемов их построения по характеристическим свойствам; 3) знание формулы расстояния между точками и умение найти это расстояние (сюда же примыкает задача о середине отрезка); 4) умение выполнить перевод с аналитического языка на графический и наоборот.
Об осознанности применения координатного метода можно судить, если учащиеся: а) дают обоснование применения графического или аналитического языка в зависимости от конкретной ситуации задачи; б) умеют наиболее рационально разместить фигуру на координатной плоскости для применения координатного метода при решении математической задачи.
На основе названных знаний и умений результаты анализа учебников можно свести в одну таблицу (табл. 14). Таблица более зримо дает возможность проследить временную последовательность изучения и применения координатного метода и установить связи между курсами математики, алгебры и геометрии, разработать целостную методику формирования метода в школе. По материалам таблицы можно дать ряд познавательных и методических задач.
Таблица 14
Анализ содержания учебного материала по координатному методу
в школьных учебниках математики
|
Знания и умения |
Учебник |
|||
|
[39] |
[40] |
[7] |
[113] |
|
|
1. Построение точки на координатном луче по ее координате 2. Сравнение чисел (натуральных и дробных) с помощью координатного луча 3. Иллюстрация действий сложения и вычитания натуральных чисел с помощью координатного луча 4. Построение точки на координатной прямой и нахождение на координатной прямой координат данной точки 5. Сравнение чисел с помощью координатной прямой. Обоснование действий сложения над положительными и отрицательными числами с помощью координатной прямой 6. Построение точки на координатной плоскости и нахождение на координатной плоскости координат данной точки 7. Чтение графиков процессов по картинкам учебника 8. Построение графиков функций и выяснение свойств функций на основе их графического изображения 9. Построение графиков уравнений и систем уравнений. Графическое решение уравнений и их систем 10. Введение координат на плоскости, координаты середины отрезка, расстояния между точками 11. Уравнение прямой и окружности и т.д. |
§ 1, п. 5
гл. I, § 1, п. 6; гл. II, § 7, п. 46 гл. II, § 2, § 7, п. 22
гл. I, § 3, п. 2
|
гл. I, § 1, п. 2
гл. I, § 1, пп.5, 6, 7 и 10
гл. I, § 1, п. 10
гл. II, § 5, пп. 14, 15, 17
гл. IV, § 16, пп. 40, 41 и др. |
§ 8
§ 8 |
|
Задание 4. Закончите анализ содержания учебного материала по координатному методу в школьных учебниках [7], [8] и [113] с целью: а) выяснения объема и последовательности его изучения и применения в восьмилетней школе; б) выявления связи изложения этого материала в курсе алгебры и в курсе геометрии. Результаты анализа запишите в таблицу (см. табл. 14).
Задание 5. На основе анализа учебного материала учебников выясните, какие знания являются «ядерными» в формировании координатного метода, в каких классах эти знания формируются, какие содержательные связи между ними установлены.
Задание 6. Проанализируйте задачи из § 8 учебника [113] и из гл. II, § 5, п. 10 учебника [8] и выберите по одной наиболее «представительной» математической задаче, эффективно иллюстрирующей все этапы реализации координатного метода в школе.
Напомним основные этапы изучения в школе координатного метода: а) перевод с аналитического языка на графический основного отношения задачи (с графического на аналитический, если задача дана на графическом языке); б) преобразование или исследование объекта на новом языке, более удобном и результативном для изучения объекта; в) перевод результата преобразования или исследования на язык решаемой задачи; г) осмысление полученного результата.
VI. Разработка конкретной методики формирования отдельных компонентов координатного метода в школе.
В формировании координатного метода в школе можно выделить несколько этапов:
1. Усвоение основного понятийного аппарата.
Это усвоение осуществляется в основном в V-VI классах и систематизируется в курсе геометрии, если этот курс активно использует данный метод, как это сделано в учебнике А.В. Погорелова.
2. Введение на основе этого понятийного аппарата уравнений линий и графиков функций.
Две эти учебные задачи решаются в разных предметах (геометрии и алгебре), с разной содержательной целью; поэтому учащиеся часто не видят между ними связи, а значит, и не усваивают главной сути метода.
3. Раскрытие основных этапов применения метода в курсах алгебры и геометрии.
4. Использование координатного метода для решения различных математических задач.
Первый этап из названных наиболее детально разработан в учебниках и не представляет трудности для учащихся.
Задание 7. Разработайте методику использования диафильма Ю. Гладкова «Координатная прямая. Координатная плоскость» (07-3-270) для формирования основного понятийного аппарата координатного метода.
3адание 8. В учебнике [113] в содержательном смысле основной понятийный аппарат координатного метода вводится вновь в VIII классе. Есть ли в этом необходимость? Если есть, то какими приемами актуализировать знания по данному вопросу, полученные в курсе алгебры, и как построить изучение этого вопроса в курсе геометрии? Предложите вариант методики изучения этого вопроса в VIII классе.
Наиболее трудным является второй этап формирования координатного метода. И трудности эти связаны с тем, что в курсе алгебры VII класса графики основных функций вводятся путем построения ряда точек, координаты которых вычисляются по аналитическому заданию функции. В курсе геометрии уравнение прямой и окружности вводится на основе геометрических характеристических свойств как множества точек, обладающих определенным свойством (равноудаленности от двух точек — для прямой и для окружности — от одной).
Строгих обоснований в курсе алгебры , что график прямой
пропорциональности есть прямая, не дается. Впервые к этому обращаются в курсе
геометрии. Разные учебники эту проблему решают методически по-разному: в одних
используется явно подобие, в других — равноудаленность от двух точек, что в
конечном счете тоже сводится к подобию, в третьих для частного случая ![]() рассматривается биссектриса первого и
третьего координатных углов и т.п.
рассматривается биссектриса первого и
третьего координатных углов и т.п.
3адание 9. Проанализируйте
учебники [6], [2] и [131] по вопросу обоснований того факта, что функции вида ![]() где k и b — числа, а х —
любое, имеют графиком прямую линию.
где k и b — числа, а х —
любое, имеют графиком прямую линию.
Оцените эффективность каждого из вариантов изложения этого материала с учетом связи с курсом геометрии и преемственности с другими вопросами алгебры.
3адание 10. Разработайте методику обобщающего урока на тему «Уравнения линий, изучаемых в школьном курсе математики». В материале урока предусмотрите, где впервые и на каком языке (алгебраическом или геометрическом) вводится каждая из линий (прямая, парабола, гипербола, окружность). Как аргументируется вид каждой линии? Какие ее свойства и на каком языке изучаются? Какие известны приемы перевода каждой из линий с одного языка на другой?
Обстоятельное рассмотрение этого этапа формирования метода дает учащимся в руки ряд приемов, помогающих использовать более эффективно координатный метод.
Третий этап может быть раскрыт на примере двух конкретных задач, аналогичных тем, которые приведены в IV разделе настоящей работы.
3адание 11. На примере задачи
«В треугольнике ![]() — медиана. Докажите, что
— медиана. Докажите, что ![]() .» разработайте методику использования
координатного метода для решения задач по геометрии.
.» разработайте методику использования
координатного метода для решения задач по геометрии.
3адание 12. Выясните специфику применения координатного метода для изучения векторов в школе.
Итоговое задание. Подберите набор математических задач из курсов алгебры и геометрии, на при мере решения которых можно будет проверить сформированность координатного метода в школе с учетом целей, поставленных в начале лабораторной работы. Выделите основные учебно-познавательные действия, владение которыми учащиеся должны показать при решении этих задач. Разработайте содержательные критерии оценки владения этими действиями и соотнесите их с обязательными результатами обучения по этому вопросу.
Результат выполнения итогового задания может быть представлен к зачету по теме «Координатный метод в школе».
Литература: [19], [20], [47], [84], [10], [11], [93], [114], [125].
Лабораторная работа № 17
Тема. Методика обучения учащихся векторному методу в школьном курсе геометрии.
Цель. Рассмотреть цели изучения векторного метода в школе, выделить основные компоненты решения задач этим методом, рассмотреть понятийный аппарат (перечислить основные понятия, которые должен знать ученик,и основные действия, которыми он должен овладеть) векторного метода решения задач, рассмотреть методику обучения учащихся векторному методу по разным учебным пособиям.
Основное содержание
1. Вектор — одно из фундаментальных понятий современной математики и широко используется в различных ее областях. В работах Г. Бесселя, Ж. Аргана и К. Ф. Гаусса по теории комплексных чисел установлена связь между арифметическими операциями над комплексными числами и геометрическими операциями над векторами в двумерном пространстве. В работах В. Гамильтона, Г. Грассмана, Ф. Мёбиуса понятие вектора нашло широкое применение при изучении свойств трехмерного и многомерного пространств. В настоящее время на векторной основе излагаются линейная алгебра, аналитическая и дифференциальная геометрия, функциональный анализ и др.
К понятию вектора как направленного отрезка приводят многие задачи механики и других областей физики: теории упругости, теории электромагнитных полей и т.д.
В методике преподавания математики вектор выступает как связующее звено между метрикой и направлением.
Цели изучения векторного метода в средней школе:
- дать эффективный метод решения различных геометрических задач (как аффинных; так и метрических) и доказательства теорем;
- по казать широкое применение векторного аппарата в других областях знаний: технике, физике, химии, лингвистике и т.д. - и на базе этого формировать у учащихся диалектико-материалистическое мировоззрение;
- использовать векторный метод при решении задач с целью формирования у учащихся умения выполнять обобщение и конкретизацию;
- формировать у учащихся такие качества мышления, как гибкость (нешаблонность), целенаправленность, рациональность, критичность и др.
2. На занятиях практикума по решению задач векторному методу уделяется большое внимание. В процессе анализа решения некоторой задачи выделяются основные компоненты решения этой задачи векторным методом.
В качестве примера можно рассмотреть решение следующей задачи:
Задача. В треугольной пирамиде DABC плоские углы при вершине D равны по 90°. Боковые ребра АD=6, DB=8, DC=24. Точка М равноудалена от всех вершин пирамиды. Найти расстояние DM.
Решение. Выберем направление осей прямоугольной
системы координат так, как показано на рисунке 23, поместив в ее начало вершину
D. Пусть М (х; у; z). Выберем базисные векторы ![]() . Тогда разложение векторов
. Тогда разложение векторов ![]() по базисным запишется так:
по базисным запишется так:

Запишем условие равноудаленности точки М от
вершин на векторном языке: ![]() или
или
![]()
![]()
![]()


![]()
![]()
![]()
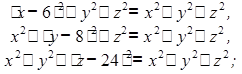



Ответ: DM=13.
Основные компоненты векторного метода решения задач
1) Перевод условия задачи на язык векторов, в том числе:
- введение в рассмотрение векторов;
- выбор системы координат (если это необходимо);
- выбор базисных векторов;
- разложение всех введенных векторов по базисным.
2) Составление системы векторных равенств (или одного равенства). Заметим, что в школе чаще используются векторные тождества и их преобразования, реже — векторные уравнения. Поэтому нами используется термин «равенство».
3) Упрощение векторных равенств.
4) Замена векторных равенств алгебраическими уравнениями и их решение.
5) Объяснение геометрического смысла полученного решения этой системы (или одного уравнения).
3. Понятийный аппарат и умения, которыми должен овладеть ученик, чтобы научиться решать задачи векторным методом:
- основные понятия: вектор, начало вектора, конец вектора, одинаково направленные векторы, противоположно направленные векторы, абсолютная величина вектора (модуль вектора), равные векторы, нулевой вектор, координаты вектора, проекция вектора на ось, коллинеарные векторы, неколлинеарные векторы, единичный вектор, координатные векторы (орты), скалярное произведение векторов, угол между ненулевыми векторами;
- основные действия, умение выполнять которые должно быть сформировано у учащихся: сложение векторов (пользуясь «правилом треугольника», «правилом параллелограмма». «правилом параллелепипеда»): вычитание векторов; умножение вектора на число; представление вектора в виде суммы, разности двух векторов, в виде произведения вектора на число; замена вектора ему равным при помощи параллельного переноса; представление вектора в виде его разложения по двум неколлинеарным векторам; переход от соотношения между векторами к соотношению между их длинами и выполнение обратного действия; выражение длины вектора через его скалярный квадрат; выражение величины угла между векторами через скалярное произведение векторов и длины этих векторов;
- действия для овладения компонентами метода: перевод геометрических терминов на язык векторов и решение обратной задачи; перевод условия задачи на язык векторов, т.е. составление системы векторных равенств по условию задачи; выбор базисных векторов, разложение всех введенных в рассмотрение векторов по базисным векторам; упрощение системы векторных равенств; замена векторных равенств алгебраическими.
4. Основные этапы формирования векторного метода у учащихся:
Подготовительный этап. Его цель — овладение перечисленными основными понятиями и основными действиями.
Мотивационный этап. Его задача — показать необходимость овладения этим методом и добиться осознания того факта, что на следующих этапах целью деятельности учащихся будет именно усвоение этого метода решения задач. Прием, используемый при этом,- решение таких задач, которые векторным методом решаются проще, чем любым другим, или другим вообще решить невозможно.
Ориентировочный этап. Его цель — разъяснить суть метода и выделить его основные компоненты на примере анализа решенной этим методом задачи.
Этап овладения компонентами метода. Цель — используя специально подобранные задачи, формировать отдельные компоненты метода (сначала задачи на формирование одного компонента, потом — двух, трех и т.д.):
Этап формирования метода «в целом». Цель — решение задач, в которых работают все или большинство компонентов метода (в том числе и на материале физики, химии и других предметов).
Деление формирования метода на этапы здесь условно, так как они тесно взаимосвязаны. Очевидно, не стоит разделять ученикам четко задачи на формирование компонентов, но сам учитель должен четко знать, какой компонент с помощью какой из задач он будет формировать у учащихся. Однако цель каждого этапа должна быть ясна и учителю, и учащимся.
Задание 1. Проанализируйте § 1О и § 17 учебника А.В. Погорелова.
1) Выполните логико-математический анализ теоретического материала.
2) Выясните, позволяет ли система задач учебника сформировать у учащихся векторный метод решения задач. (При подготовке ответа на этот вопрос учтите, что среди задач этого учебника отсутствуют такие, при решении которых необходимо все введенные векторы разлагать по базисным; нет задач, на которых можно было бы показать приложение векторного аппарата в других областях знаний, кроме математики и др.)
3) Выясните, достаточно ли в данной системе задач для формирования каждого из вводимых (например, в § 10) понятий при обучении теоремам, содержащимся в этом параграфе. Назовите номера задач и укажите, на формирование какого понятия и выработку какого умения «работает» та или иная задача.
Задание 2. На основе анализа выполненного задания 1, сформулируйте цели изучения векторного метода в IX и XI классах.
Задание 3. Какая математическая трактовка понятия вектора принята в учебнике А.В. Погорелова? Напишите реферат по статье А.Д. Александрова (см. [14]). Оцените достоинства и недостатки каждого из подходов для изучения математики и ее приложений.
Методика формирования векторного метода решения задач
I. Подготовительный этап формирования метода (понятийный аппарат, основные понятия и основные действия) имеется в каждом из рассматриваемых учебных пособий, хотя он и не сосредоточен на каком-либо коротком промежутке времени.
II. На мотивационном этапе можно рассмотреть с учащимися решение следующей задачи:
Задача. В трапеции ABCD углы А и В равны по 90°, а стороны АВ=2, ВС=1, AD=4.·Докажите, что диагонали этой трапеции взаимно перпендикулярны.
Задача решается несколькими способами и показывается, что векторный метод решения задачи более прост.
1 способ (рис. 24)
![]()
![]() что и требовалось доказать.
что и требовалось доказать.
Задание 4. Разработайте другие способы решения этой задачи, не связанные с использованием векторного метода. Сравните эти способы решения и оцените эффективность каждого.
Задание 5. Решите задачу:
«Точки ![]() и
и ![]() являются
соответственно точками пересечения медиан граней ABD и BCD тетраэдра ABCD. Доказать разными
методами, что
являются
соответственно точками пересечения медиан граней ABD и BCD тетраэдра ABCD. Доказать разными
методами, что ![]() : а) векторным; б) координатным; в)
традиционным; г) геометрических преобразований. Какой из методов решения этой
задачи эффективнее?
: а) векторным; б) координатным; в)
традиционным; г) геометрических преобразований. Какой из методов решения этой
задачи эффективнее?
Задание 6.
III. На примере решения первой задачи проведите ориентировочный этап, т.е. разъясните суть метода и покажите его основные компоненты:
1) Выясняется, что нужно доказать на геометрическом языке.
- Что для этого достаточно доказать на векторном языке?
- Какую операцию осуществили?
2) Есть ли в условии
задачи векторы ![]() и
и ![]() ?
?
-
Каким
образом можно получить векторы ![]() и
и ![]() ?
?
3) Записывается скалярное произведение векторов.
4) Выполняются
преобразования и получается, что ![]() .
.
5) Переводится векторное равенство на геометрический язык.
Показывается, как можно формировать выделенные компоненты векторного метода.
Первое действие, которому необходимо научить учащихся, - это перевод геометрических соотношений на векторный язык. Для формирования умения выполнять это действие целесообразно с учащимися решать задачи типа
1. Точка А принадлежит отрезку ВС. Запишите
это соотношение в векторной форме. ![]()
2. Прочитайте запись на геометрическом языке ![]() . (Точка М принадлежит прямой АВ.)
. (Точка М принадлежит прямой АВ.)
3. Отрезки АВ и МК параллельны. Запишите
это соотношение в векторной форме. ![]()
4. Точка С — середина отрезка АВ. Как
это соотношение записать в векторной форме? ![]()
5. Прямые АС и МР параллельны. Как записать это соотношение в векторной форме? Есть ли разница в записи решений задач 3 и 5? Почему?
6. Запишите в векторной форме условие
перпендикулярности прямых АВ и РK. ![]()
Решение этих и других подобных задач желательно оформить в виде таблицы в кабинете и первое время ею пользоваться при решении задач векторным методом.
Учащимся показывается наиболее целесообразный выбор системы координат (в том случае, когда это необходимо) и выбор базисных векторов.
Это действие формируется у учащихся с помощью задач:
Замечание. В задачах 1 и 2 система координат выбирается произвольно, после чего строятся точки по координатам и условие задачи записывается в векторной форме.
Самостоятельная работа
1. Проанализируйте пробные учебники по геометрии Л.С. Атанасяна и др. [45], [46], [47] и А.Д. Александрова и др. [17], [18], [19], [20], [16] и ответьте на вопросы:
1) Какова трактовка понятия «вектор», принятая каждым авторским коллективом?
2) Какие элементы векторного аппарата и в каких классах вводятся?
3) Позволяет ли система задач сформировать понятийный аппарат, отдельные компоненты векторного метода и векторный метод решения задач в целом?
2. Пользуясь указанной ниже литературой, подберите системы задач на формирование каждого компонента векторного метода.
Литература: [45], [65], [92], [113], [118], [129], [127].
Лабораторная работа № 18
Тема. Метод геометрических преобразований при изучении математики в школе.
Цели. Выделить характеристические признаки метода геометрических преобразований и рассмотреть особенности его изучения по различным школьным учебникам математики.
План
Основное содержание
Сущность любого математического метода, в том числе и метода геометрических преобразований, состоит в построении модели одной теории (в нашем случае традиционной евклидовой геометрии) в объектах другой (группы геометрических преобразований). Существенным признаком математической модели является наличие изоморфизма между моделью и моделируемой теорией. Установим наличие указанного изоморфизма между множеством точек и прямых евклидовой плоскости и множеством инволюционных элементов группы движений, т.е. множеством осевых и центральных симметрий. Каждой точке А ставится в соответствие центральная симметрия с центром в данной точке А, каждой прямой а — осевая симметрия с осью а.
Различные отношения между точками и прямыми евклидовой плоскости могут быть интерпретированы с помощью композиций осевых и центральных симметрий. Например, отношение «точка А принадлежит прямой а» соответствует тому, что композиции центральной симметрии относительно центра А и осевой с осью а, осевой относительно прямой а и центральной с центром А представляют собой одно и то же преобразование плоскости, т.е.
![]()
Наличие указанного выше изоморфизма и позволяет применять метод геометрических преобразований при решении задач, сформулированных в терминах евклидовой геометрии.
Метод геометрических преобразований в школе используется как средство обоснования некоторых отношений между элементами евклидовой геометрии (например, конгруэнтности, параллельности и т.д.). При этом его применение обычно предполагает выполнение следующей последовательности шагов:
- выбирается геометрическое преобразование, обладающее свойством, которое позволяет обосновать наличие указанного отношения между объектами евклидовой геометрии;
- выполняется преобразование, при котором один объект переходит в другой;
- обосновывается наличие указанного отношения между объектами с помощью свойств выбранного геометрического преобразования.
Выделенные шаги использования метода геометрических преобразований обусловливают необходимость актуализации основных понятий теории геометрических преобразований и свойств (общих и специфических) отдельных видов преобразований и овладение умением строить образы фигур при том или ином преобразовании.
Покажем реализацию выделенной последовательности шагов при решении следующей задачи методом геометрических преобразований:
3адача. На высоте BD треугольника АBC имеется точка К, такая, что АK=KC. Докажите, что треугольник АBC равнобедренный (рис. 25).
В задаче необходимо установить конгруэнтность отрезков АB и BC (или равенство их длин).
Первый шаг состоит в выборе геометрического преобразования, которое обладает свойством сохранять расстояние. Именно это свойство позволит обосновать отношение конгруэнтности между отрезками АВ и BC. В качестве такого преобразования целесообразно выбрать осевую симметрию относительно прямой BD.
Второй шаг состоит в том, чтобы доказать, что при симметрии относительно прямой BD отрезок АВ перейдет в отрезок СВ. Это можно доказать довольно просто. Точка В перейдет сама в себя при выбранной симметрии, так как она является точкой оси симметрии. Точка А перейдет в C при данной симметрии, так как эти точки на перпендикуляре к оси симметрии и АK=CK (К — точка оси симметрии).
Третий шаг — заключительный этап решения задачи. Так как отрезки АВ и СВ симметричны относительно оси BD, а симметрия является перемещением (движением), то длины отрезков АВ и СВ (или BC) равны.
К основным понятиям теории геометрических преобразований можно отнести понятия отображения, преобразования, перемещения (движения), обратного преобразования, способа задания геометрического преобразования, конкретные виды геометрических преобразований.
К общим свойствам геометрических преобразований относятся следующие:
- композиция перемещений (движений) есть перемещение (движение);
- преобразование, обратное перемещению (движению), есть перемещение (движение);
- при перемещении (движении), а также при преобразовании подобия прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки; при указанных преобразованиях сохраняются углы между полупрямыми.
- при перемещении (движении) точки, лежащие на прямой, переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Выделяются специфические свойства каждого из конкретных видов геометрических преобразований (осевой и центральной симметрий, поворота, параллельного переноса, гомотетии, преобразования подобия), рассматриваемых в школьном курсе математики.
Для каждого вида преобразования актуализируется способ построения образа фигуры при соответствующем преобразовании.
Геометрические преобразования в школе рассматриваются, во-первых, как объект изучения и, во-вторых, как основной инструмент метода.
В систематическом курсе геометрии изучаются преобразования фигур на плоскости и в пространстве. При этом преобразование фигуры понимается как ее смещение. Среди преобразований выделяются движения и преобразование подобия. Рассматриваются частные виды движении: осевая симметрия, центральная симметрия, поворот, параллельный перенос. Частным видом преобразования подобия является гомотетия.
Выделим основные понятия и свойства, связанные с частными видами геометрических преобразований (на основе анализа учебника [113]).
Результатом этой работы может быть заполнение таблицы (табл. 15).
Таблица 15
|
Название вида геометрического преобразования |
Основные понятия, связанные с его изучением |
Свойства геометрического преобразования |
|
Центральная симметрия
. . . |
Центр симметрии. Центрально-симметричные фигуры (точки) относительно центра. Центрально-симметричная фигура
|
Преобразование симметрии относительно точки является движением. (Все свойства движения применимы к центральной симметрии)
|
Необходимо обращать внимание на задание того или иного вида преобразования, отдельно оговаривать набор умений, которые формируются у учащихся при рассмотрении видов преобразований.
Затем необходимо выяснить, какие виды преобразований рассматриваются в пропедевтическом курсе геометрии (V — VI классы), какие знания и умения формируются при их рассмотрении.
Задание 1. Выполните анализ системы задач, помещенных после пунктов «Центр симметрии» и «Ось симметрии» (см. [40]).
Итогом работы может быть заполнение таблицы (табл. 16).
Таблица 16
|
Вид преобразования |
Способ задания (на координатной плоскости, в пространстве) |
Теоретический материал, при рассмотрении которого используются свойства прео6разования |
|
|
|
|
Задание 2. Выполните анализ решения задачи, текст которой приведен в задании 3 для самостоятельной работы.
Выделите этапы решения этой задачи методом геометрических преобразований. Выделите умения, которыми должны овладеть учащиеся, чтобы использовать метод при решении данной задачи.
Разработайте методику поиска решения данной задачи.
После этого переходите к анализу системы задач, помещенных после § 9 учебника [113]. Выделите задачи, направленные на усвоение знаний о геометрических преобразованиях; задачи, решаемые методом геометрических преобразований.
Определите количественное соотношение этих задач и обоснуйте его.
Для получения необходимых обобщений об изучении метода геометрических преобразований в школе выполните логико-дидактический анализ материала, связанного с геометрическими преобразованиями в неполной средней школе.
Самостоятельная работа
1. Составьте список основных понятий, используемых в теории геометрических преобразований, и основных свойств отдельных геометрических преобразований, рассматриваемых в школьном курсе математики.
2. Выделите понятия в пропедевтическом и систематическом курсах геометрии, которые вводятся с помощью геометрических преобразований (см. [113]).
Выделите теоретический материал, при изучении которого используется метод геометрических преобразований.
3. Решите задачу, использовав метод геометрических преобразований, и выделите основные этапы ее решения.
Задача. Точка В лежит между точками А и С. По одну сторону от прямой АС построены равносторонние треугольники АЕВ и BFC. Доказать, что треугольник с вершинами в серединах отрезков AF и ЕС и точке В равносторонний.
4. Выполните логико-математический анализ теоретического материала § 9 из учебника [113].
5. Выполните анализ системы задач к § 9 учебника [113]. Выделите и решите задачи, в которых целесообразно использовать метод геометрических преобразований.
Индивидуальные задания
1. Выделите типы задач, используемые для формирования понятия о геометрических преобразованиях фигуры: а) в учебнике [23]; б) в учебнике [24].
2. Установите особенности изучения метода геометрических преобразований по учебнику [45].
3. Приведите примеры использования метода геометрических преобразований при изучении курса алгебры.
Литература: [40], [45], [113], [125], [18].
Лабораторная работа № 19
Тема. Методы дифференциального исчисления в школьном курсе математики.
Цели. 1. Актуализировать знания о методе дифференциального исчисления.
2. Определить место, цели и значение изучения метода дифференциального исчисления в школе.
3. Показать, что рассматриваемый метод — важнейший аппарат изучения естественных наук и математики.
4. Рассмотреть возможность применения метода при изучении математики.
5. Установить межпредметные связи.
Оборудование. Диафильмы «Непрерывные функции», 07-3-446; «Предел функции. Производная», 07-3-139.
Основное содержание
I. Для достижения поставленных целей необходимо решить следующие методические задачи:
1. Установить содержание метода дифференциального исчисления.
2. Установить цели изучения этого метода в школьном курсе «Алгебра и начала анализа».
3. Определить знания и умения, которыми должны овладеть учащиеся при изучении метода.
4. Уточнить содержание и уровень изложения соответствующего учебного материала, выделив «ядерный» и сопутствующий (неосновной) материал.
Одна из задач курса «Алгебра и начала анализа» заключается в завершении изучения функциональной линии курса алгебры неполной средней школы, где учащиеся знакомятся с основными понятиями, результатами, методами математического анализа в объеме, который позволяет исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи.
Общая учебная задача, которая может быть поставлена при изучении элементов математического анализа, - изучить метод, позволяющий применять понятие производной к решению различных учебно-практических задач.
Без понимания метода математического анализа невозможно разобраться в естественных науках, в технической и научно-популярной литературе. Это обусловлено тем, что математика проникает во все области деятельности человека.
Фундаментальным методом математического анализа является дифференциальное исчисление.
Основная идея метода дифференциального исчисления состоит в том, что, зная функцию и указав точку (или не указывая ее), можно дать локальную характеристику изменения функции при изменении аргумента.
Метод дифференциального исчисления выступает методом математического анализа, так как с его помощью изучаются свойства различных классов функций. Кроме того, производная выступает инструментом и языком, на котором описываются многие процессы естествознания и техники, исследуются и изучаются многие явления реального мира.
Математика применяется в естествознании и технике для расчетов и количественных характеристик. Но получить расчетную формулу, например, траектории ракеты или прочности балки трудно Здесь и используется аппарат математического анализа, который дает возможность по исследованию бесконечно малых элементов линий (поверхностей) — дифференциальное исчисление — в результате получить требуемые формулы для объекта в целом — интегральные исчисления.
Обращение к бесконечно малым дает возможность «кусок» кривой заменить отрезком (секущей или касательной), установить какие-либо закономерности, используя отрезки, проще, чем дуги кривых.
II. Выяснив суть метода дифференциального исчисления, необходимо обратить внимание на образовательные, развивающие и воспитательные цели изучения рассматриваемого метода:
- систематизировать знания о функциях, которые имеются у учащихся к началу изучения темы;
- ознакомить с новым методом исследования свойств функции;
- показать применение нового метода исследования свойств функций к решению различных прикладных задач;
- разъяснить учащимся, что метод дифференциального исчисления — мощнейший аппарат познания законов природы, и раскрыть роль этого аппарата для практики;
- выявить широкие возможности более глубокого и всестороннего воспитания диалектико-материалистического мировоззрения.
Указанных целей можно достичь после самостоятельного анализа соответствующих разделов программы по математике для средней общеобразовательной школы [119].
III. Анализ программы и учебного пособия по математике дает основание дать правильные ответы на следующие вопросы:
Задание 1.
1) Каков понятийный аппарат метода дифференциального исчисления?
2) В чем специфика этого метода математического анализа?
3) Какие знания и умения необходимо актуализировать для сознательного и прочного овладения методом дифференциального исчисления?
4) Какие знания и умения формируются при изучении метода?
Детальное обсуждение поставленных вопросов приводит к следующим выводам:
Сознательное усвоение метода дифференциального исчисления невозможно без введения фундаментальных понятий, таких, как приращение аргумента и приращение функции, отношение этих приращении, производная, тангенс угла наклона касательной, проведенной к графику функции в указанной точке, предельный переход.
Метод дифференциального исчисления является основным методом исследования различных процессов, решения различного класса задач, поэтому учащимся необходимо знание всех названных понятии. Решение задач позволяет сделать интуитивно ясными такие понятия, как непрерывность функции, производная, геометрический и механический смысл производной и применение ее к приближенным вычислениям; сформулировать критерии возрастания и убывания функции, признаки минимума и максимума. Весьма важным является решение учебно-практических задач средствами математического анализа, так как на этом материале учащихся знакомят с построениями математических моделей и их решениями.
Для успешного и сознательного овладения методом необходимо актуализировать знания и умения учащихся.
Знания:
- функции числового аргумента;
- приращения аргумента и функции;
- скорости неравномерного движения, средней скорости, мгновенной скорости;
- таблицы производных элементарных функций.
Умения:
- находить значение функции в точке;
- находить приращение функции по заданному приращению аргумента;
- находить отношение приращения функции к приращению аргумента при заданных условиях;
- находить среднюю скорость неравномерного движения.
В результате изучения метода учащиеся должны приобрести знания:
- определений понятия производной, точки максимума, точки минимума;
- алгоритма нахождения производной, составления уравнения касательной к кривой в указанной точке;
- плана исследования функций и построения графика;
- основных формул дифференцирования, включая сложную функцию;
- геометрического смысла производной и интеграла;
- физического смысла производной;
- достаточного условия возрастания (убывания) функции.
Считается, что учащиеся овладели методом, если в результате изучения материала у них удалось сформировать умения:
- находить производную функцию в точке и на отрезке;
- использовать понятие производной для исследования свойств функции;
- устанавливать характер изменения функции по знаку производной;
- выявлять точки, подозрительные на экстремум;
- вычислять наибольшее (наименьшее) значение функции на отрезке;
- применять метод дифференциального исчисления для решения сюжетных задач (математических и физических);
- применять понятие производной для приближенных вычислений.
IV. Указанные выше цели и поставленные задачи дают возможность выделить «ядерный» и сопутствующий материал, который позволит учащимся усвоить рассматриваемый метод.
«Ядерным» материалом являются определения понятия производной и алгоритм нахождения производной.
Сопутствующим материалом в первом случае — примеры вычисления производных элементарных функций, дифференцируемость функций.
Обучение методу дифференциального исчисления не должно сводиться к сообщению определения производной и на основе определений вычислениям производной. Чтобы учащиеся убедились, что дифференцирование действительно является методом математического анализа, необходимо рассмотреть различные по фабуле и требованиям задачи из разных областей знаний.
Приведем примеры таких задач:
Задача 1. Определить
скорость тела, движущегося прямолинейно по закону ![]() (м), в момент времени t=5 с.
(м), в момент времени t=5 с.
Задача 2. В тонком
неоднородном стержне длиной 35 см масса (в граммах) распределена по закону ![]() , где l — длина части стержня,
отсчитываемая от начала. Найти плотность в точке, отстоящей от начала на 3 см.
, где l — длина части стержня,
отсчитываемая от начала. Найти плотность в точке, отстоящей от начала на 3 см.
Задача 3. Закон свободного
падения тела в пустоте определяется формулой ![]() , где g — постоянная
величина. Найти скорость этого движения в некоторый фиксированный момент
времени
, где g — постоянная
величина. Найти скорость этого движения в некоторый фиксированный момент
времени ![]() .
.
Анализ решения приведенных задач позволяет обнаружить, что при поиске ответов на поставленные требования каждый раз выполнялась одна и та же последовательность операций. Можно привести еще много задач из техники, физики, для решения которых необходимо вычислять предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю. Оказалось целесообразным выделить такой предел, дать ему термин «производная» и изучить его основные свойства. После введения термина формулируется определение производной, которое является конструктивным, что позволяет «построить» алгоритм вычисления производной в точке.
На основе определения производной формулируются теоремы о дифференцировании суммы, произведения, частного двух функций, рассмотрен частный случай дифференцирования сложной функции («внутренняя» функция — линейная) и постулируется, что это верно и в общем случае.
3адание 2.
1) Установите, какие знания необходимо актуализировать для понимания геометрического смысла производной.
2) Составьте серию задач, с помощью которой раскрывается геометрический смысл производной.
3) Выясните, какие свойства функций изучаются с помощью производной.
4) Составьте серию задач, с помощью которой вырабатывается аппарат данного метода.
5) Выясните, какие формы контроля эффективно использовать для определения сформированности метода.
Перечисленные задания для самостоятельной работы предполагают групповую форму работы.
V. Далее рассматривается возможность применения метода дифференциального исчисления при изучении различных вопросов математики, раскрывается методика установления межпредметных связей.
Реализовать эти цели можно при решении следующих методических задач:
3адание 3.
1) Разработайте серию тестовых задач на экстремум, которая позволит выяснить алгоритмическое предписание, с помощью которого в дальнейшем будет осуществляться решение таких задач.
2) Разработайте методику формирования умения применять изученный метод для составления уравнения касательной к графику функции в указанной точке, определите шаги алгоритма.
3) Установите, на каких задачах целесообразно показать применение метода дифференциального исчисления для приближенных вычислений значений функции.
4) Приведите примеры физических, технических задач, на которых можно показать установление межпредметных связей.
В результате анализа нескольких серий задач формулируется предписание решения текстовых задач на нахождение наибольшего (наименьшего) значения. Предписание имеет следующие шаги:
- установить переменные и постоянные, используемые в задаче, и установить, какая из переменных исследуется;
- составить математическую модель задачи (в данном случае функцию, наибольшее или наименьшее значение которой требуется определить);
- найти производную функции;
- вычислить критические точки функции;
- выбрать критические точки, которые принадлежат промежутку;
- вычислить значение функции в критических точках, лежащих внутри промежутка и на его концах;
- установить вид экстремума в критических точках внутри промежутка с помощью достаточного-условия экстремума;
- из всех полученных чисел выбрать наименьшее (наибольшее);
- записать ответ.
Следует обратить внимание на то, что полученное предписание не будет усвоено учащимися формально, если оно является следствием решения серии математических задач.
Результатом решения второй методической задачи является предписание, состоящее из шагов:
- найти производную функции;
- вычислить значение производной в указанной точке;
- сравнить значение производной с нулем;
а) если значение производной в данной точке вычислить
нельзя, то либо касательную в этой точке провести нельзя, либо касательная
перпендикулярна оси x, ее уравнение ![]() ;
;
б) если значение производной равно нулю, то
касательная в данной точке параллельна оси x, ее уравнение ![]() ;
;
в) если производная существует и ее значение отлично от нуля, то в этой точке можно провести касательную к кривой, наклоненную к оси x;
- вычислить значение функции в указанной точке;
-
составить
выражения ![]() и
и ![]() ;
;
- из полученных выражений составить равенство.
Остановиться необходимо на частичном решении четвертой методической задачи, привести примеры только применения производной к решению физических и технических задач.
3адание 4. Какими математическими задачами можно продолжить предложенный список математических задач и какова должна быть методика их решения, чтобы можно было считать, что учащиеся понимают значение метода математического анализа для других областей знаний?
Примеры задач:
1. Вычислить работу электрического тока, напряжение которого меняется со временем.
2. Длина стержня равна 10 см, а его линейная плотность
в точке, находящейся на расстоянии x см от левого конца, равна ![]() (г/см). Определить массу стержня.
(г/см). Определить массу стержня.
Итоговое задание. Разработайте содержание учебного материала с при влечением данных из истории развития математического анализа, на основе которого можно показать различие методов изучения свойств функций элементарными средствами (с помощью уравнений и неравенств) и с помощью методов математического анализа.
Литература: [5], [9], [10], [50], [96], [115], [37], [70].
Глава III
ПРАКТИЧЕСКИЕ PAБОТЫ ПО МЕТОДИКЕ ПРЕПОДАВАНИЯ МА ТЕМАТИКИ
§ 8. ЛОГИКО-ДИДАКТИЧЕСКИЙ АНАЛИЗ ТЕМЫ
Существенной особенностью практических работ по сравнению с лабораторными является выполнение логико-дидактического анализа тем школьных учебников и на основе этого анализа решение различных методических задач.
Выполнение лабораторных работ позволяет осмыслить структуру отдельных компонентов учебного материала, систематизировать основные формы организации учебного процесса, средства обучения, формы контроля и оценки.
На основе этих знаний и умений можно приступать к логико-дидактическому анализу завершенных в математическом отношении тем. Тема школьного учебника — именно та единица учебного материала, которая позволяет раскрыть логическую и математическую организацию и трактовку взаимосвязанных между собой вопросов, выяснить уровень строгости рассматриваемых фактов, сравнительно четко выделить и сформулировать цели изучения основных вопросов, очертить возможные варианты средств обучения, продумать систему контроля и оценки законченной системы знаний и умений.
Так как вся последующая методическая работа на практических занятиях строится на основе выполненного логико-дидактического анализа тем школьных учебников, то дадим более подробную трактовку этого вопроса.
Логико-дидактический анализ темы представляет последовательность действий: определение цели обучения теме; логический и математический анализ содержания темы (теоретического и задачного материала); постановка основных учебных задач и выбор соответствующих учебно-познавательных действий; отбор основных средств, методов и приемов обучения; определение форм контроля и оценки процесса и результата учебной деятельности учащихся.
Рассмотрим более подробно каждое из действий логико-дидактического анализа темы.
Определение цели обучения теме. В ситуации обучения в классе цель изучения темы задается учителем. Следовательно, стоит методическая проблема — обеспечение принятия цели учеником, так как цель, сформулированная учителем, далеко не всегда становится целью деятельности ученика В таких условиях, как отмечают психологи, связь формируется от цели к мотиву. Эта ситуация отлична от той, когда у самого человека возникает потребность что-то узнать, и тогда он ставит перед собой цель — достичь желаемого результата. В этом случае мотив порождает цель. Будем понимать цель как предвидение результатов и тех действий (в основном учащегося), которые ведут к достижению этих результатов. Под результатами понимаются не только содержательные факты, но и умения выполнять действия, ведущие к осознанному и глубокому владению фактами в разнообразной учебной деятельности.
Чтобы цель, поставленная учителем, стала целью ученика, она должна приобрести личностный смысл для него. А последнее становится возможным, если она будет соответствовать мотиву его деятельности. Другими словами, эта цель должна осмыслиться каждым учащимся, т.е. каждый должен понять, зачем надо изучать ту или иную тему.
Между мотивами и целью существует очень сложная зависимость и тесная связь. В процессе целеобразования, т.е. принятия субъектом цели, необходимо, чтобы осознание будущего результата осмысливалось с пониманием, зачем этот результат нужен учащемуся, и происходило слияние цели и мотива. Поэтому часто в практике мотивы и цели не разделяются. Чисто в учебных целях ниже приведем примеры возможного четкого разделения целей и мотивов и их связь и примеры, где цели и мотивы сразу выступают во взаимосвязи.
Если подвести итог этому очень краткому анализу проблемы «цель — мотив», то следует заметить: цель направлена на результат деятельности, мотив — на то, где этот результат может быть использован.
Действие целеполагания очень сложное действие, так как оно связано со многими фактами и явлениями. Чтобы выполнить постановку цели обучения теме и ее мотивацию, необходимо:
- ознакомиться с целями изучения курса (в состав которого входит анализируемая тема), которые записаны в программе по математике;
- ознакомиться с примерным тематическим планированием, обычно предлагаемым журналом «Математика в школе»;
- ознакомиться с примерными межпредметными связями внутри предмета;
- на основе логико-математического анализа темы знать ее «ядерный» и сопутствующий ему материал и уровень логической строгости изучения «ядерного» материала.
Выполнив названные выше действия, можно высказать предвидимый результат обучения в форме теоретических фактов и умений. Для создания положительного мотива необходимо показать:
- возможные практические приложения знаний и умений, приобретенных в результате изучения темы;
- интересные факты из истории получения и использования фактов и методов темы;
- широкую или красивую применимость методов и приемов, рассматриваемых в теме;
- занимательную задачу, софизм и т.п., разрешение которых станет возможным благодаря изучению данной темы и т.п.
Материал для создания отдельных элементов мотивации положительного отношения к предмету можно найти почти по всем темам в журнале «Квант», в книгах Г.И. Глейзера ([48], [49], [50]), в «Энциклопедическом словаре юного математика» ([141]) и др. Кроме того, полезным средством для мотивации и целеполагания является ознакомление с реальными трудностями учащихся при изучении темы путем непосредственного посещения школы и беседы с учителями и учащимися. В целях слияния мотива и цели в ходе изучения темы необходимо постоянно стремиться к созданию подлинно познавательного интереса, в основе которого применительно к предмету математики лежит овладение учебно-познавательными действиями и математическими методами и приемами.
Логико-математический анализ содержания темы. Логический анализ темы прежде всего сводится к установлению логической организации учебного материала в ней с учетом специфики аксиоматического метода. Ранее (см. § 7) мы отмечали возможных три способа логической организации материала: на содержательной основе, дедуктивный подход к построению курса, построение на дедуктивной основе.
Установив логическую организацию учебного материала в теме, необходимо выяснить, какие утверждения доказываются, какие вводятся как иллюстрированные факты, каков уровень логической строгости доказательств, какой метод используется для доказательства, какие новые теоретические утверждения вводятся при решении математических задач.
Математический анализ сводится к выяснению основной математической идеи темы (ответ на вопрос, о чем в этой теме узнаем), к выяснению математических обоснований выполняемых преобразований исследований доказательств, к осмыслению применяемых в теме математических методов и приемов.
Результатом выполнения логико-математического анализа будет определение «ядерного» материала, логической строгости его изучения и математических методов и приемов изучения этого материала. Во второй главе настоящей работы были показаны различные приемы логико-математического анализа основных компонентов учебного материала: определений, теорем, алгоритмов, математических методов и математических задач. Ими возможно воспользоваться и при анализе тем. Кроме того, вузовские курсы математики направлены на оказание помощи в раскрытии трактовок тем школьного курса математики. Учебные пособия по курсу методики преподавания математики (в особенности частные методики) также содержат материал, на основе которого возможно выполнять логико-математический анализ тем.
На основе логико-математического анализа теоретического материала темы выполняется анализ математических задач.
При анализе математических задач темы необходимо получить ответ на ряд основных вопросов:
1) Какое количество задач способствует раскрытию, конкретизации, углублению «ядерного» материала темы?
2) Как сгруппированы задачи в соответствии с «ядерным» материалом темы (все ли задачи, соответствующие одному вопросу, собраны в одну группу или перемежаются задачами на повторение)?
3) Объединив задачи в группы только с целью анализа, если этого нет в учебнике, можно ли назвать несколько задач, «представителей» группы, на решении которых должно быть сосредоточено внимание в классе с последующим закреплением приемов и методов решения таких задач?
4) Как связаны группы задач, направленных на изучение «ядерного» материала, с задачами из обязательных результатов обучения по теме?
5) Есть ли в общем наборе задач задачи на осуществление поиска решения, т.е. задачи как средство формирования математической деятельности на школьном уровне? Сколько таких задач? Достаточно ли их для достижения поставленных целей?
6) Есть ли математические задачи, показывающие приложение изучаемых вопросов в ранее изученных темах математики и других дисциплин?
7) Есть ли задачи, учитывая возраст учащихся, изучающих тему, на основе которых можно создавать положительную мотивацию учения (занимательные, с нестандартной фабулой, проблемные и т.п.)?
Результатом анализа математических задач будет в каждой теме своя типология; основные задачи, которые необходимо решать в классе; методическое отношение к остальным задачам.
Постановка основных учебных задач. Как отмечалось ранее (гл. I, § 3), учебная задача включает в себя результат (в обобщенном виде) и действия, к нему ведущие. Поэтому в ходе логико-дидактического анализа темы необходимо сформулировать основные теоретические результаты изучения темы, учитывая их уровень обобщенности. Причем теоретические результаты меньше всего включают в себя знание отдельных конкретных фактов как объектов, на усвоение которых направлены усилия учащихся, а в значительной мере — типы (виды) определений с их логическими структурами, типы теорем, специфику методов и приемов, типологию математических задач.
Это первая особенность постановки учебных задач.
Так как,для достижения отмеченных результатов необходимо отобрать адекватные учебно-познавательные действия, то второй существенной особенностью постановки учебных задач при изучении темы будет отбор и определение приемов выполнения учебных действий.
Обычно для обучения конкретным темам ставится две-три общие учебные задачи. При планировании уроков по изучению темы эти учебные задачи конкретизируются, выделяются подзадачи, решения которых в целом позволяют решить и общую учебную задачу. В конкретных темах на основе поставленной цели и выполненного логико-математического анализа их содержания будут показаны примеры постановки учебных задач.
Отбор основных средств и методов обучения. Когда поставлена учебная задача, то выбор средств и методов обучения в значительной мере предопределен. Действия решения учебной задачи входят в ее постановку. Специфика формирования этих действий зависит от их операционного состава, от уровня подготовки класса в предшествующем обучении, от тех средств, которыми располагает школа (ТСО, ЭВМ, таблицы, дидактические материалы, тетради с печатной основой, магнитная доска и т.п.), от личных умений и способностей учителя. Поэтому решать вопрос отбора средств обучения можно только вариативно с учетом объективных возможностей материала. Все остальное будет уточняться в конкретной школе, классе и у конкретного учителя.
Несколько иначе решается вопрос о выборе приемов и методов обучения. Учитель должен в зависимости от содержания учебного материала варьировать методы как по источникам обучения, так и по учету видов деятельности учащихся. Во время изучения темы ученики могут и с учебником поработать, могут и послушать объяснение учителя или товарища. Одни темы лучше изучать алгоритмическими методами (действия над числами, тождественные преобразования и др.), в других больше удельный вес исследовательских методов (исследование функций, решение неравенств, решение задач по геометрии и др.).
Окончательный ответ на этот вопрос тоже может дать только анализ конкретной темы.
Формы контроля и оценки процесса и результатов деятельности учащихся при обучении теме. Поскольку в цели изучения темы входит предвидение результатов и действий, к нему ведущих, то и оцениваться должны не только результаты, но и действия.
Одной из особенностей учебной деятельности в отличие, например, от трудовой является то, что в равной, если не в большей мере, ее результатом должно быть овладение действиями учения, а не только присвоенными фактами (теоретическими чаще всего). Естественно, в ходе присваивания фактов происходит в разной мере овладение действиями учения. Но коль скоро мы оцениваем знание фактов и конечный результат решения математических задач, то и усилия учеников чаще всего направлены на запоминание факта и получения результата математической задачи любыми средствами: угадать, подогнать под ответ, обратиться к помощи родителей или старших или списать готовое решение у товарища.
Поскольку чаще всего оцениваем результат, ученик и стремится любыми средствами получить результат и предъявить его для оценки.
В учебном процессе в равной мере должно оцениваться овладение действиями, как учебно-познавательными, так и собственно математическими.
В постановке учебной задачи обязательно должны указываться действия, которыми должны овладеть при решении этой задачи учащиеся. В организацию контроля должны войти задания, проверяющие уровень сформированности тех или иных действий. Особенно важно продумывать действия, направленные на достижение обязательных результатов обучения теме. Таким образом, учебно-познавательные действия, спрогнозированные в целях обучения теме, конкретизировались в учебной задаче, в методах и приемах изучения темы и должны получить оценку в контролируемых результатах.
Выполнение всех пяти компонентов логико-дидактического анализа темы позволяет составить тематический план изучения темы, определить конкретно цели каждого отдельного урока как звена в общей цепи изучения темы, организовать деятельность учащихся на уроке и т.п.
На фоне выполненного логико-дидактического анализа темы или хотя бы основных ее компонентов: постановка цели и логико-математический анализ содержания — можно решать частные методические задачи. Если же анализа темы нет, вся последующая работа будет малоэффективна. Подготовить план урока вне контекста его в теме невозможно, подобрать средства обучения вне анализа содержания невозможно и т.п. Поэтому-то главным профессиональным умением учителя считаем умение выполнять логико-дидактический анализ тем. Все остальные профессиональные умения формируются на его основе.
В настоящей главе на основе логико-дидактического анализа ряда тем школьных учебников будет показано решение некоторых методических задач.
8.1. Логико-дидактический анализ темы «Многоугольники»
Анализ темы «Многоугольники» будет выполнен по учебнику А.В. Погорелова [113].
1. Цели образовательные и воспитательные изучения темы «Многоугольники». 1. Продолжить раскрытие содержания геометрии как дедуктивной системы знаний:
а) построить систему определений основных фигур темы на основе логической связи их между собой;
б) раскрыть конструктивную природу определений многоугольника и угла с учетом нового подхода (как части плоскости);
в) раскрыть операционный состав единого математического приема неполной индукции, используемого при доказательстве основных утверждений темы, и степень строгости проводимых доказательств.
2. Систематизировать и обобщить некоторые метрические свойства многоугольников, рассмотренные ранее для треугольников и четырехугольников и в связи с окружностью.
3. Типизировать математические задачи, раскрыть операционный состав поиска решений задач определенных типов, показать практические приложения изучаемой в данной теме теории.
Непосредственными мотивами изучения этой темы могут быть следующие:
1) Весь понятийный аппарат темы составит основу понятийного аппарата темы «Многогранники» в курсе стереометрии.
2) Изучаемые свойства правильных многоугольников применяются при конструировании различных деталей (гайки восьмиугольные и шестиугольные) и сооружений (можно решить задачи № 21, 22, 40).
3) Теория и практика паркетов построена на свойствах многоугольников и особенно правильных многоугольников (статья А.Н. Колмогорова «Паркеты и правильные многоугольники», [72]).
4) На основе свойств правильных многоугольников можно решать интересные задачи на разбиение фигур (см.: Квант.-1982. - № 12). Решение таких задач развивает логическое и конструктивное мышление учащихся.
2. Логико-математический анализ темы. Материал в теме организован на дедуктивной основе, так как всем фигурам, вводимым в теме, даются определения. Можно проследить логическую цепочку в конструировании определений фигур.
Выстроенная цепочка позволяет решать вопросы раскрытия логического действия — конструирования определений объектов.
Математический анализ этой цепочки связанных понятий показывает, что наиболее трудными для объяснения будут понятия плоского и выпуклого многоугольников, так как здесь используются такие объекты, как часть плоскости и принадлежность прямой полуплоскости. Названные понятия вводятся на основе иллюстраций, и этот факт накладывает определенные требования на использование наглядности. Существенно новым и важным для данного курса геометрии является вводимое здесь понятие плоского угла. Так как по современной программе вопросы, связанные с длиной дуги и радианной мерой угла, изучаются в связи с изучением тригонометрических функций, то 'здесь данные понятия можно только актуализировать.
В теме доказывается четыре утверждения. Одно — о длине ломаной — фактически есть обобщение неравенства треугольника. Второе — о сумме углов выпуклого многоугольника — есть обобщение утверждения о сумме углов треугольника. Третье — конструктивная теорема существования правильного многоугольника. И четвертое дает в определенной мере обоснование числа π.
В основе доказательства первых двух утверждений лежит идея обобщения неравенства треугольника и суммы углов треугольника, она же используется и как прием доказательства. От одного неравенства треугольника переходим к следующему звену и т.д. и индуктивно делаем общий вывод. Аналогичный прием и в двух следующих теоремах. Поэтому необходимо раскрыть операционный состав приема и суть умозаключения по индукции, чтобы были усвоены и действия, приводящие к обоснованию утверждения.
Значительные содержательные сложности скрыты в доказательстве теоремы об отношении длины окружности к диаметру, так как здесь неявно используется понятие предела. Опять важно использование средств наглядности, особенно здесь хорошо использовать мультфильм.
Факты, связывающие длину стороны правильного многоугольника с радиусом окружности, устанавливаются в значительной мере алгебраически.
Математические задачи, приведенные в учебнике, можно по соответствию теоретическим сведениям объединить в пять групп: первая группа задачи - № 1-7, вторая - № 8-18, третья - № 19-29, четвертая - № 30-40, пятая - № 41-47.
В соответствии с обязательными результатами решение «типичных» задач второй, третьей и четвертой групп должно быть хорошо отработано в классе и со всеми учащимися. для определения «типичных» задач необходимо наборы групп задач учебника сравнить с обязательными результатами и выделить их пересечение. В каждой из групп есть задачи, решая которые можно формировать основные элементы математической деятельности на школьном уровне. Из первой группы это задачи № 5, 7; из второй - № 9, 13, 14, 15, 16, 18; из третьей - № 23, 24, 25; из четвертой - № 38, 39.
Выделение основного («ядерного») материала темы, установление групп математических задач, соответствующих основному материалу, выделение «типичных» задач группы и задач, позволяющих обучать математической деятельности, позволяют определить основные учебные задачи и действия по их решению.
3. Учебные задачи и действия, им адекватные. Основной учебной задачей темы, как вытекает из целей обучения теме и анализа содержания учебного материала, может быть формирование нового понимания геометрической фигуры как части плоскости и раскрытие некоторых ее конструктивных и метрических свойств на основе решения математических задач.
При решении этой учебной задачи можно решить следующие подзадачи:
а) Раскрыть логическую структуру взаимосвязи определений фигур темы от ломаной до правильного многоугольника. Результатом решения этой подзадачи будет «цепочка» взаимосвязанных определений и умения конструировать их, выделяя родовое свойство и видовые отличия. Материал темы позволяет (сконцентрировано в одном месте восемь взаимосвязанных объектов) действие конструирования определений фигур сделать актуально значимым.
б) Раскрыть структуру приема доказательства утверждений по индукции. Результат решения — овладение последовательностью действий, составляющих прием доказательства по индукции.
в) Раскрыть соотношение между линейными и угловыми элементами правильных многоугольников и радиусами вписанной и описанной окружностей и конкретизировать его при решении математических задач. Результат решения — последовательность действий при применении формул к решению математических задач, так как эти действия в значительной мере однообразны во всех задачах. А именно эти задачи составляют основное содержание задач обязательных результатов обучения.
г) Раскрыть специфику получения формулы длины окружности (на основе интуитивного понимания понятия «близко» между периметрами вписанного и описанного правильных многоугольников) и применить ее к нахождению длин окружностей и их частей. Результат решения — понимание особого приема доказательства теоремы и последовательность операций по применению формулы в аналогичных задачах.
д) Овладеть приемами поиска решения математических задач путем использования общих приемов решения задач на доказательство и конкретных эвристик, использующих выведенные в теме свойства фигур. Результат решения — актуализированные общие приемы поиска решения задач на доказательство и специфические эвристики.
4. Средства и приемы обучения. Средства: модели плоских и неплоских ломаных; модели и чертежи многоугольников (выпуклых, невыпуклых, правильных, вписанных и т.п.); магнитная доска, складной метр; динамическая модель описанного и вписанного многоугольников; математические задачи как средство подведения под понятие фигуры и конкретизации теоретического факта; математические задачи как цель реализации математической деятельности на школьном уровне.
Приемы: использование графов для
построения «родословной» понятия; составление пошагового доказательства теоремы
12.1 для создания возможностей переноса структуры доказательства на
доказательство последующих теорем: 12.2 и 12.3; работа с учебником при
доказательстве теорем 12.2 и 12.3; составление таблиц формул для ![]() и
и ![]() через R и r
и представление их в классе для постепенного, непроизвольного запоминания;
набор эвристик при обучении поиску решения задач.
через R и r
и представление их в классе для постепенного, непроизвольного запоминания;
набор эвристик при обучении поиску решения задач.
5. Формы контроля и оценки. Контролироваться и
оцениваться при обучении данной теме будет следующее: 1) знание основных («ядерных»)
фактов: определения правильного многоугольника; теоремы существования
правильного многоугольника (возможности вписания (описания) правильного
многоугольника в окружность); формулы, выражающей зависимость ![]() от R и r,
обоснования числа π, плоского угла; 2) владение методом доказательства
по индукции, приемом составления «родословной» взаимосвязанных определений
фигур; приемом обоснования числа π; общими приемами решения задач,
конкретизирующих теоретические факты на уровне обязательных результатов
обучения; общими приемами поиска решения нестандартных математических задач.
от R и r,
обоснования числа π, плоского угла; 2) владение методом доказательства
по индукции, приемом составления «родословной» взаимосвязанных определений
фигур; приемом обоснования числа π; общими приемами решения задач,
конкретизирующих теоретические факты на уровне обязательных результатов
обучения; общими приемами поиска решения нестандартных математических задач.
На основе логико-дидактического анализа темы, который возможно выполнять с разной степенью детализации и конкретизации, можно далее решать различные методические задачи.
В частности, на первых практических занятиях, после того как будут усвоены общие подходы выполнения логико-дидактического анализа тем, необходимо решить методическую задачу: «Составить таблицу — развернутый тематический план изучения темы «Многоугольники» (табл. 17)».
Дадим комментарий к каждой графе.
1. Количество уроков взять пока такое же, как в программе, так как нет учета работы реального класса и конкретного учителя (см.: Математика в шк.- 1985. - № 6).
2. Темы уроков сформулировать на основе логико-дидактического анализа темы, но каждый урок должен иметь свою тему.
3. Цели уроков детерминированы только содержанием материала и получат корректировку в реальном классе. Сформулированные ранее учебные задачи и подзадачи существенно помогают постановке целей урока.
4-5. Распределение математических задач по урокам и на домашние и классные детерминируется целями урока и обязательными результатами обучения (см.: Математика в шк.- 1985. - № 3).
6. Самостоятельные работы зависят от реализуемых целей и вида деятельности учащихся на уроке. Их содержание приведено в журнале «Математика в школе».- 1985. - № 1. В этой графе важно предусмотреть степень самостоятельности выполнения учащимися каждой самостоятельной работы: работа проводится с указанием общих рекомендаций о ее выполнении, с использованием учебников и тетрадей, с использованием консультаций учителей или товарищей, полностью самостоятельно без какой-либо помощи и т.п.
Таблица 17
Методическое планирование темы «Многоугольники»
|
№ урока |
Тема урока |
Цель урока |
Распределение задач |
Самостоятельные работы |
ТСО и наглядные пособия |
Повторение |
Материал для мотивации |
|
|
в классе |
дома |
|||||||
|
1 |
Ломаная и выпуклый многоугольник |
Сформировать действие распознавания фигур |
Построение и распознавание фигур |
№ 8 |
Все учащиеся распознают фигуры под руководством учителя |
Складной метр, картинки, кодопозитивы |
Неравенство треугольника ([113]) Сумма углов треугольника ([113]) |
[53], с. 26; [53], с. 27, № 72 и 7.8 |
|
2 |
Свойства ломаной и выпуклого многоугольника |
Раскрыть сущность метода доказательства по индукции на теореме 12.1 |
- |
№ 4, № 5 |
Разобрать по учебнику в классе под руководством учителя теорему 12.2 |
На кодопозитиве основные этапы доказательства теоремы 12.2 |
Вопросы № 1 и 3 |
[53], К.27, № 72 и 7.8 |
|
3 |
Правильный многоугольник и его свойства |
Формировать действие конструирования определений |
№ 11, № 12 |
№ 14 и формулы на с. 156-157 |
По учебнику разобраться в доказательстве теоремы 12.3 |
Диафильм «Многоугольник и его свойства» |
Диафильм «Многоугольник и его свойства» |
[49], с. 95 |
|
4 |
Построение правильных многоугольников. Решение задач |
Раскрыть операции способов построения правильных многоугольников |
№ 13,30,31, 17 |
№ 18,19,23 |
С -10 (№ 41) с целью проверки сформированности свойств ломаной |
Кодопозитив с рис. 191 ([113]) |
|
[110], с. 53; [49], с. 96 |
|
5 |
Решение задач на прямое применение изученных теорем |
Раскрыть приемы использования теорем 12.1, 12.2, 12.3 при решении задач |
№ 2,19,24, 26 |
№ 21, № 28 |
Все решают задачи в классе |
Алгоритм по поиску решения задач |
Теоремы 12.1, 12.2, 12.3 |
|
|
6 |
Решение задач по изученному материалу |
Актуализировать общие приемы решения задач и учиться пользоваться эвристиками |
№ 15, № 25 |
№ 16, № 26 |
С-11 с использованием учебника и рабочих тетрадей |
Кодопленки с эвристиками и схемами поиска решения |
Систематизация свойств вписанных (описанных) многоугольников |
[110], с. 54 |
|
7 |
Центральный угол. Длина окружности |
Раскрыть прием доказательства теоремы 12.4, сконструировать новое определение угла |
— |
№ 32, № 41 |
Самостоятельно вычленять этапы доказательства теоремы 12.4 |
Модель разъемной окружности. Диафильм «Длина окружности» |
Угол, окружность, свойство 6 правильного многоугольника |
Задачи с практическим содержанием |
|
8 |
Радианная мера угла. Длина окружности |
Ввести новую меру угла и на ее основе показать алгоритм нахождения углов и длины дуг |
№ 47 (1-3), № 44 (1-3) |
№ 44 (4-6), № 42 (4-6) |
С-12 с целью контроля умения применять формулы |
На кодопленке варианты С-12 и результаты решения для проверки в классе |
Измерение угла градусной мерой |
[49], с. 98 |
|
9 |
Решение задач по урокам 7 и 8 |
Раскрыть возможности применения формул с переносом в новые ситуации |
№ 45 (1-3), № 46 (1-2) и на нахождение длины окружности |
№ 4, № 45 (3), и по записи |
Все решают задачи в классе |
Кодопозитивы для проверки решения задач |
|
|
|
10 |
Решение задач по теме «Многоугольники» |
Показать решение нестандартных задач, подготовиться к контрольной работе |
№ 38, 39, 9 |
№ 38 (3), № 10 |
С-13 с использованием учебника |
Кодопозитивы для проверки решения задач |
|
|
|
11 |
Контрольная работа |
Проверить умения использовать материал темы |
|
|
Два варианта из [57] |
|
|
|
|
12 |
Анализ контрольной работы и урок-обобщение |
Обобщить цепочку определений и метод доказательства. Проанализировать ошибки |
Аналоги контрольной работы |
По выбору две задачи |
|
|
|
|
7. В графе «ТСО и наглядность» можно использовать результаты анализа темы и конкретные изготовленные наглядные пособия. а также диафильмы и диапозитивы.
8. Повторение необходимо спланировать с учетом целей обучения.
9. Материал, способствующий созданию положительной мотивации, можно найти в книгах для внеклассной работы.
Составленное примерное методическое планирование темы не является обязательным и предметом обсуждения на занятиях.
Достоинствами предложенного планирования можно считать объединение в один урок всего понятийного аппарата правильных многоугольников, объединение в один урок доказательства двух теорем, так как метод доказательства их одинаков, концентрацию на небольшом числе уроков изучения теории с целью выделения большего времени для решения различных задач, а не только задач из группы, принадлежащей изучаемой теории, и т.п.
На материале этого планирования можно поставить следующие методические задачи:
3адача 1. Разработайте план урока по введению всего понятийного аппарата темы. Предложите систему наглядности и набор вопросов, помогающих установить существенные свойства объектов и логические связи между определениями объектов темы.
3адача 2. Проанализируйте группу математических задач с № 19 по 29. Расположите их по степени нарастания сложности. Предложите методику решения «типичной» задачи группы. Как «типичная» задача связана с обязательными результатами обучения и как это учтено в методике ее обучения?
3адача 3. Разработайте методику использования исторического материала при изучении данной темы. Предложите приемы вовлечения учащихся в ознакомление с историческим материалом.
3адача 4. Разработайте таблицу, в которой были бы представлены в обобщенном виде (вариант опорного конспекта) основные факты темы. Такую же таблицу можно составить по методам, используемым в теме, и по приемам поиска решения математических задач.
3адача 5. Предложите формы контроля и критерии оценки сформированности учебных и математических действий и операций по итогам изучения темы «Многоугольники».
8.2. Логико-дидактический анализ темы «Неравенства»
1. Обучение теме можно начать с создания положительных мотивов ее изучения. Широким познавательным мотивом здесь могут выступать изучение свойств числовых неравенств, методы решения линейных неравенств с одной переменной и их систем. Учебно-познавательным мотивом может быть интерес к анализу доказываемых неравенств, получению выводов. Примером мотивации может служить разбор «доказательства» софизма «Положительное число меньше нуля».
Пусть а и b произвольные положительные числа, удовлетворяющие неравенству
![]()
Умножим (1) на b-a:

Однако ![]() где
где ![]() есть число положительное, так как квадрат
числа, отличного от 0,
положителен.
есть число положительное, так как квадрат
числа, отличного от 0,
положителен.
Соотношение (2) позволяет утверждать, что положительное число меньше 0.
Или другой пример мотивации:
Какое из выражений принимает большее значение при всех значениях переменной:
![]() или
или ![]() ?
?
Как сравнить два выражения? Укажите основные операции сравнения.
Третий пример: Укажите значения площади боковой поверхности прямоугольного параллелепипеда, если его линейные измерения найдены в границах
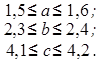
В технике используются понятие «допуски», допускаемые отклонения числовой характеристики каких-либо параметров (например, в деталях машин и механизмов) от их расчетного значения в соответствии с заданным классом точности. Допуски широко используются в машиностроении, строительстве и многих других областях. Вычисление допусков требует знания действий с числовыми неравенствами, которые выполняются на основании свойств числовых неравенств.
Кроме указанных познавательных мотивов, очень важны для учащихся этого возраста узкие социальные мотивы, в частности, может быть использован мотив овладения способом налаживания сотрудничества в учебном труде.
2. Известно, что неравенства. как условные, так и безусловные, широко используются в трудовой деятельности человека, а также в самой математике. Исходя из этого перед учащимися ставится учебная задача: сформировать общие и специфические учебные действия доказательства безусловных неравенств решения линейных неравенств и их систем для получения общего способа выяснения интервалов знакопостоянства, возрастания и убывания изучаемых функций.
Эту задачу можно считать решенной, если будут решены такие учебные подзадачи:
- выяснить способ доказательства безусловных неравенств, выделив специфические учебные действия;
- раскрыть характеристики оценки результатов действий над переменными, значения которых находятся в заданных границах;
- определить компоненты учебного действия «перевод задания числового промежутка с одного «языка» на другой»;
- раскрыть алгоритм решения линейного неравенства с одной переменной;
- выявить алгоритм решения системы линейных неравенств с одной переменной;
- сформировать предписание, которое позволяло бы устанавливать промежутки знакопостоянства, возрастания, убывания функций определенного вида.
3. Решение названных подзадач будет осуществляться в ходе выполнения учащимися соответствующих учебных действий, общих и специфических.
Такими специфическими действиями, характерными для сформулированных задач, будут:
- составление разности выражений, стоящих в левой и правой частях неравенств;
- выполнение тождественных преобразований;
- установление знака разности выражений;
- подведение под понятия «больше», «меньше»;
- изображение промежутка, заданного его концами, на координатной прямой и запись промежутка на «языке» неравенств;
- алгоритм решения линейного неравенства с одной переменной;
- алгоритм решения системы линейных неравенств с одной переменной;
- определение границ выражения, если переменные заданы своими границами.
Операционный состав этого действия может быть фиксирован в такой последовательности:
а) установить границы каждой переменной. входящей в выражение;
б) выяснить, с помощью каких действий над переменными и числами получено выражение;
в) определить порядок действий;
г) вычислить последовательно границы результата каждого действия, используя свойства неравенств;
д) записать, в каких границах находится данное выражение;
- установление характера изменения функции при заданных значениях аргумента.
Операционный состав этого действия следующий:
а) выбрать два произвольных значения аргумента из указанного промежутка;
б) сравнить значения ![]() и
и ![]()
в) найти значения ![]() и
и ![]()
г) сравнить соответствующие значения функции (**);
д) выяснить одинаковость смысла числовых неравенств (*) и (**);
е) получить вывод о характере изменения функции на указанном промежутке;
- найти промежутки знакопостоянства.
Здесь отмечены только специфические учебные действия, однако при решении подзадач будут использоваться и такие учебно-познавательные действия, как, например, распознавание, выведение следствии, сравнение и сопоставление, конкретизация общего способа решения для данной задачи и др.
4. Логический анализ темы «Неравенства» дает основание
сделать вывод, что тема организована дедуктивно-индуктивно, так как дано
определение понятии «больше», «меньше»; свойства числовых неравенств
сформулированы в виде теорем, которые доказаны; сформулированные теоремы
равносильности (названные свойствами) не доказываются. Алгоритмы доказательства
безусловных неравенств, решения линейных неравенств с одной переменной и
решения систем линейных неравенств введены индуктивно на конкретных примерах,
анализ решения которых и позволяет учителю, сделав обобщение, сформулировать
алгоритмы. Структура вводимых определении (решения неравенств, равносильных
неравенств, решения системы неравенств) одинакова, а следовательно, их изучение
может осуществляться по одному плану, т.е. на уровне теоретического обобщения.
Теоремы о свойствах неравенств имеют одну и ту же структуру: ![]() , а это позволяет осуществить перенос
знаний, так как с теоремами такой структуры учащиеся работали уже в предыдущем
классе.
, а это позволяет осуществить перенос
знаний, так как с теоремами такой структуры учащиеся работали уже в предыдущем
классе.
Вводятся понятия нестрогого и строгого неравенств, линейного неравенства, системы неравенств.
5. «Ядерным» материалом темы являются:
- понятия «больше», «меньше», неравенства, решения неравенства, решения системы неравенств, равносильных неравенств;
- свойства числовых неравенств, равносильных неравенств;
- операции над числовыми неравенствами;
- алгоритмы решения неравенств с одной переменной и решения системы неравенств;
- прием доказательства безусловных неравенств и прием использования неравенства для выяснения возрастания, убывания функции.
Изложение материала опирается на алгебраические операции, тождественные преобразования, понятие координатной прямой, законы арифметических действий.
При доказательстве свойств числовых неравенств используются логические правила вывода, определения «больше», «меньше».
При изучении темы могут быть выбраны информационно-словесный, репродуктивный методы, а в некоторых случаях — метод проблемного изложения (например, решения системы неравенств с одной переменной).
6. К средствам обучения математике можно отнести все, что будет способствовать реализации целей обучения данной теме, в первую очередь серии задач (вопросов). (Здесь задачи могут выступать и как средство обучения, и как цель изучения.) Так, учебная подзадача «Выяснить способ доказательства безусловных неравенств, выделив специфические учебные действия» может быть решена обобщением решения типичной конкретно-практической задачи. Учащимся предлагается типичная задача:
«Докажите неравенство ![]() ».
».
Учащиеся знают, что сравнить выражения возможно, составив разность и определив знак этой разности, что для этого следует упростить полученную разность, выполнив тождественные преобразования.
В данном случае разность тождественно равна выражению ![]() , значение которого при всех значениях а
положительно. Значит, при любых значениях а верно данное
неравенство, т.е.
, значение которого при всех значениях а
положительно. Значит, при любых значениях а верно данное
неравенство, т.е.
![]()
Анализ решения задач дает возможность установить операции и их последовательность.
Решение одной задачи не позволяет говорить о сформированности умения доказывать неравенства; поэтому учащимся предлагается серия задач, которая может быть, например, такой:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Предложенный набор задач охватывает все возможные случаи, а следовательно, можно утверждать, что позволяет сформировать учебное действие «доказывать неравенства».
При решении учебных подзадач «Определить компоненты учебного действия "перевод задания числового промежутка с одного языка на другой" и «Выявить алгоритм решения системы линейных неравенств с одной переменной» может быть использована магнитная координатная прямая с двумя-тремя прозрачными цветными полосками (целлофан, лавсан, полиэтилен).
Естественно, что решения можно показать, пользуясь только доской и мелом, но магнитная координатная прямая имеет ряд преимуществ: не надо вычерчивать координатную прямую, не надо заштриховывать, переход к новому заданию не занимает много времени (не надо стирать с доски и вычерчивать новый чертеж). Кроме того, яркий зрительный образ позволяет повысить активность и внимательность.
Здесь же может быть использована подвижная модель координатной прямой с двумя цветными полосками. Такая модель индивидуального пользования может быть изготовлена самими учащимися и использована на уроке при фронтальной работе.
Смена средств обучения способствует активизации деятельности учащихся, что в свою очередь позволяет улучшить усвоение материала.
При решении учебных задач «Установление характера изменения функции при заданных значениях аргумента», «Нахождение промежутков знакопостоянства» целесообразно использовать рабочие таблицы с подвижной координатной осью. Такие таблицы позволяют активизировать внимание учащихся, улучшить запоминание. Применение таких таблиц способствует интенсификации обучения, так как учитель не тратит время на вычерчивание графиков, а сразу приступает к работе с классом. Аналогом таблицы может служить кодопозитив, на котором изображена кривая, а координатная плоскость, выполненная на оргстекле, накладывается на изображение кривой. Такое пособие дает возможность предлагать учащимся серию задач (вариации получаются за счет перемещения координатной плоскости).
При изучении этой темы целесообразно использовать диафильм «Числовые неравенства и их свойства» (07-3-094), который является важным средством обучения, так как дает возможность иллюстрировать объяснение учителя, организовывать учебную деятельность учащихся, проверку их знаний, уровня сформированности умений.
7. При изучении темы «Неравенства» можно использовать различные приемы организации учебной деятельности учащихся. Укажем некоторые из них.
(А) Прием заполнения пустых мест таблицы (табл. 18).
Таблица 18
|
№ п/п |
Неравенство |
Изображение решения на координатной прямой |
Запись решения |
|
1
2
3
4
5
6 |
3<x<6
... x<5
- 4<x ... 3 |
(3; 6)
...; 10]
[-3; ...
[4; ∞) |
(Б) Сравнение решения задачи с помощью алгоритма и без него. Этот прием дает возможность воспитывать творческий подход, показывать важность анализа условия задачи.
Например, доказать неравенство
![]()
Решение
![]() или
или ![]()
(В) Прием составления серии задач с нарастающей сложностью преобразований. Этот прием может быть использован при формировании умения решать линейные неравенства.
Например, можно предложить учащимся такую серию задач:
![]()
(Г) Прием поиска ошибки в данном «решении» позволяет воспитывать критичность мышления, более глубоко осознавать теоретический материал.
Например, найти ошибку в «решении» и сформулировать правила или свойства неравенств, на которые допущены ошибки:
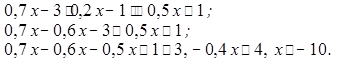
(Д) Прием, который
позволяет сформировать потребность самоконтроля, объяснить, почему данные
решения неверны.
Например:
а) ![]() б)
б) ![]() в)
в) ![]()
Решения отвергаются обоснованно, учащиеся должны аргументировать свои ответы.
(Е) Могут быть использованы задания с выборочными ответами, а также прием работы с книгой, прием. построения алгоритма решения определенного класса задач. В нашем случае это алгоритмы решения неравенств и системы неравенств с одной переменной.
Остановимся на приеме построения алгоритма как результата теоретического обобщения решения задач. Здесь эффективно может быть использована групповая форма работы на первом этапе построения алгоритма.
Класс разделить на четыре группы, каждой группе дать одно из заданий:
а) ![]()
б)![]()
в)![]()
г)![]()
1-й шаг — упростить выражение каждой части неравенства (воспользоваться сопоставлением решения уравнения и неравенства).
2-й шаг — перенести члены неравенства, содержащие переменную, в одну часть, числа — в другую с изменением знака на противоположный (используются свойства равносильности неравенств).
3-й шаг — привести подобные члены.
После третьего шага работа ведется фронтально.
4-й шаг — разделить (если возможно) обе части неравенства на коэффициент при переменной (используются свойства равносильности неравенств), получить простейшие неравенства:
а) ![]() б)
б) ![]()
в) нет решений; г) у - любое число.
5-й шаг — отметить решения на координатной прямой.
При разборе решения выделяются существенные и несущественные связи с уже изученным материалом. Анализ решения позволяет записать алгоритм решения линейного неравенства:
- раскрыть скобки в обеих частях неравенства;
- перенести слагаемые, содержащие переменную, в одну часть, а не содержащие — в другую;
- привести подобные члены в каждой части;
-
разделить
обе части неравенства на коэффициент при переменной (с учетом свойств
равносильности при ![]() );
);
- записать ответ в виде простейшего неравенства;
- отметить соответствующие промежутки на координатной прямой;
- записать числовой промежуток.
Алгоритм решения неравенства вида ![]() который является составной частью
приведенного выше алгоритма, записывается в виде схемы (рис. 26).
который является составной частью
приведенного выше алгоритма, записывается в виде схемы (рис. 26).
В результате
аналогичной работы учащиеся под руководством учителя составляют алгоритм
решения системы линейных неравенств с одной переменной:
- решение каждого неравенства системы (по алгоритму решения линейного неравенства);
- нанесение на координатную прямую числового промежутка, являющегося решением каждого неравенства;
- выделение промежутка, который удовлетворяет одновременно всем неравенствам системы;
- запись общего промежутка.
8. При изучении темы «Неравенства» могут быть использованы различные формы организации учебной деятельности учащихся.
О групповой форме организации учебной деятельности уже упоминалось. Здесь отметим, что такая форма весьма эффективна, так как, во-первых, воспитывает потребность в общении и взаимопомощи; во-вторых, формирует умение аргументировать свои действия, что способствует осознанности и прочности усвоения изучаемого материала.
Одной из разновидностей групповой формы является работа учащихся парами. Например, каждый учащийся выполняет задание партнера, а затем они вместе обсуждают решения, оценивают друг друга.
Индивидуальная форма работы реализуется при самостоятельном изучении теоретического материала о свойствах равносильных неравенств с одной переменной. В этом случае закрепляется общеучебное действие — чтение учебного материала, выделение главной мысли, установление связи с ранее изученным материалом.
Учащиеся должны ответить на вопросы:
1) Какие из пар неравенств равносильны и почему:
а) ![]() б)
б) ![]() в)
в) ![]() ?
?
2) Какие из неравенств ![]() равносильны неравенству
равносильны неравенству ![]() ? Почему?
? Почему?
3) Какой вид имеет неравенство, равносильное неравенству
![]() ?
?
Усвоение материала проверяется фронтально, учитель по изученному материалу и выполненным заданиям проводит беседу с учащимися.
9. Контроль знаний учащихся проводится в различных формах.
В частности, при изучении темы «Неравенства» могут быть использованы такие формы контроля:
1) Устная контрольная работа. Она дает возможность учителю установить, сформировано ли учебное действие «доказательство неравенства» и усвоены ли знания свойств числовых неравенств. Такую работу лучше проводить в начале урока с последующим разбором. Задания оформляются на кодопленке в двух вариантах.
2) Самостоятельные работы учащихся (2-3 человека). Решение оформляется на кодопленке для самопроверки правильности выполнения работы каждым учащимся.
3) Самостоятельная работа для всего класса в нескольких вариантах. Таких работ должно быть несколько для выяснения знания «ядерного» материала и умений при менять изученные алгоритмы. Например, самостоятельная работа может быть предложена для выяснения уровня сформированности умения «решать системы линейных неравенств с одной переменной». В эту работу включаются задания с учетом обязательных результатов обучения.
Учитель может использовать самостоятельные работы № 47-55 (см. [79]).
В теме «Неравенства» тематическим планированием предусматривается три контрольные работы, в содержание которых уже заложены обязательные результаты обучения.
При изучении материала, при проведении самостоятельных и контрольных работ учитель может ознакомиться со статьей Л. В. Кузнецовой и С. С. Минаевой «Об организации учебного процесса с учетом обязательных результатов обучения» (см.: Математика в шк.- 1986.- № 4).
Рассмотрим один из вариантов типизации задач по теме «Неравенства» по учебнику [7] (табл. 19).
Таблица 19
|
№ пункта учебника |
Основное понятие |
Тип задачи |
|
26 |
а больше b а меньше b |
Сравнение значений выражений при заданных значениях переменной (№ 617-621) Доказательство безусловных неравенств (№ 622-629) |
|
27 |
Свойства числовых неравенств |
Использование свойств неравенств (№ 635-643). Оценка значений выражений (№ 645-648) |
|
28 |
Сложение и умножение числовых неравенств |
Задачи как средство обучения действиям над неравенствами (№ 651-653) Задачи как цель математической деятельности по вычислению границ выражения (№ 654-660) |
|
29 |
Числовые промежутки, двойное неравенство |
Задачи как средство обучения: а) переводу с «языка промежутка» на «язык» геометрический (№ 667-669); б) осмыслению неравенства, двойного неравенства (№ 664-666, 671); в) изображению простейших неравенств (№ 670) и принадлежности числа промежутку (№ 672-678) |
|
30 |
Равносильность неравенств, свойства равносильности, алгоритм решения линейного неравенства |
Задачи как средство обучения: а) свойствам равносильности (№ 683-685); б) понятию решения неравенства (№ 686-687); в) сравнению двух выражений (№ 690-691). Задачи как цель математической деятельности: а) по решению неравенств (№ 688, 692-693, 695-696, 698-700); б) по решению текстовых задач на составление неравенств (№ 707-710) |
|
31 |
Решение системы неравенств, алгоритм решения системы неравенств |
Задачи как средство обучения: а) понятию решения системы (№ 715-716); б) понятию двойного неравенства (№ 722, 730, 731) Задачи как цель математической деятельности по формированию алгоритма (№ 717-721, 723-730, 734-736) |
|
32 |
Нули функции, интервалы знакопостоянства |
Задачи как средство обучения: а) на сравнение значений функции (№ 722-724); б) на нахождение значений функции (№ 741, 745-746); в) на нахождение интервалов знакопостоянства по графику (№ 747-749) и по аналитическому заданию функции |
|
33 |
Возрастание, убывание функции, характер изменения линейной функции |
Задачи как средство обучения: а) на осмысление понятия возрастания (убывания) функции (№ 759-763); б)на применение теоретического материала о характере изменения линейной функции (№ 764-766, 767) |
По данному материалу могут быть решены следующие методические задачи:
3адача 1. Разработайте методическое планирование темы, аналогичное приведенному в § 8 настоящей главы.
3адача 2. Составьте обучающую программу для использования ЭВМ по вопросу решения линейных неравенств.
3адача 3. На основе анализа темы выделите возможные исследовательские действия и разработайте методику их формирования.
3адача 4. Подберите систему практических задач, на основе решения которых возможно показать применение систем линейных неравенств для решения задачи оптимизации.
3адача 5. Разработайте конспект урока. на котором будет формироваться алгоритм решения системы линейных неравенств.
§ 9. МЕТОДИКА ИЗУЧЕНИЯ ТЕМЫ «ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ»
В КУРСЕ АЛГЕБPЫ И НАЧАЛ АНАЛИЗА
План изучения темы
Задания для самостоятельной работы
(Цель. Подготовка к реализации первой части плана)
1. Установите цели и содержание обучения алгебре и началам анализа [126].
2. Познакомьтесь с тематическим планированием учебного материала по алгебре и началам анализа в XI классе, специально выделив при этом планирование материала по теме «Первообразная и интеграл» (см.: Математика в школе.- 1986.- № 3.- С. 44).
I. Введение понятий «первообразная», «интеграл»
Цель. Установить место, цели изучения понятий «первообразная», «интеграл» в курсе алгебры и начал анализа XI класса; выявить некоторые особенности введения указанных понятий.
Оборудование. 1. Набор кодопозитивов с условиями задач для введения понятия «первообразная», задач, которые целесообразно использовать для установления связей между понятиями «первообразная», «интеграл».
2. Схема взаимосвязей между понятиями, свойствами понятий темы «Первообразная и интеграл».
План реализации первой части работы
1. Установление цели, места изучения вопросов, связанных с понятием «интеграл».
2. Изложение содержания учебного материала темы.
3. Выполнение практических заданий, связанных с анализом материала темы в школьных учебных пособиях.
4. Выводы.
Основное содержание
1. Основная образовательная цель изучения темы «Первообразная и интеграл» может быть сформулирована следующим образом:
- познакомить учащихся с операцией, которая является обратной по отношению к операции дифференцирования функций;
- познакомить с использованием метода интегрального исчисления для решения геометрических задач, некоторых задач практического содержания.
Воспитательная и развивающая цели изучения указанной темы связаны с формированием диалектико-материалистического мировоззрения («Развитие у учащихся правильных представлений о природе математики, сущности и происхождении математических абстракций, соотношении реального и индивидуального, ... месте математики в системе наук и роли математического моделирования в научном познании и в практике ... » [119]):
- ввести новый метод решения ряда задач (в частности, нахождение площади, объема фигуры), показать известную универсальность математических методов;
- продемонстрировать основные этапы решения прикладных задач средствами математики.
Теме «Первообразная и интеграл» предшествует тема «Производная и ее применение». Такая последовательность изучения материала создает предпосылки для
во-первых, понимания учащимися взаимосвязи между операциями дифференцирования и интегрирования функции, а также основной идеи метода дифференциального и интегрального исчислений (зная функцию, можно установить характер локальной ее изменяемости в зависимости от изменения аргумента, и наоборот: зная характер локальной изменяемости функции, можно найти либо саму функцию (при заданных начальных условиях), либо семейство функций);
во-вторых, осознания учащимися того факта, что аппарат производной и интеграла — основа метода математического анализа: с одной стороны, он выступает как язык, описывающий многие явления, процессы мира; с другой — как инструмент, с помощью которого с учетом особенностей языка исследуются эти явления и процессы.
2. Основу содержания темы составляют два круга вопросов, каждый из которых группируется около двух понятий: «первообразная», «интеграл».
В связи с понятием первообразной рассматриваются определение этого понятия, основное свойство первообразной (в том числе его геометрический смысл), правила нахождения первообразных.
Поскольку «задача отработки навыков нахождения
первообразных не ставится» (Математика в шк.- 1986.- № 3.- С. 44), то
упражнения, которые учащиеся должны уметь решать, ограничиваются несложными
задачами на применение правил нахождения первообразных. Программа по математике
для средней школы предполагает знание учащимися первообразных степенной функции
с целым (![]() ) показателем, функций синус и косинус.
) показателем, функций синус и косинус.
С понятием «интеграл» связано рассмотрение вопросов о площади криволинейной трапеции, приближенном вычислении интегралов, получении формулы Ньютона-Лейбница.
В качестве примеров, иллюстрирующих применение интеграла к решению различных задач, в основном рассматриваются задачи на нахождение площадей криволинейных трапеций. Вопросу вычисления объемов тел с помощью интеграла уделяется внимание, но этот материал становится предметом специального изучения в курсе геометрии (в учебном пособии А.В. Погорелова [113] общая формула для нахождения объемов тел вращения используется для получения формулы, позволяющей найти объем шара и его частей).
Таким образом, основное внимание при изучении темы уделяется, во-первых, нахождению первообразных и вычислению интегралов на базе таблицы первообразных и правил нахождения первообразных; во-вторых, вычислению площадей криволинейных трапеции.
3амечание. Еще раз хотим обратить внимание, что поскольку программа по математике не предусматривает формирование у учащихся навыков интегрирования, а нацеливает лишь на обращение к простейшим случаям применения формул для нахождения интеграла данной функции, то овладение техникой интегрирования не предполагается.
3. Выделим ряд практических заданий, на выполнение которых целесообразно ориентироваться в процессе анализа материала темы «Первообразная и интеграл» и которые связаны с ответом на следующие вопросы:
1) Каковы задачи изучения рассматриваемой темы?
Ответ на поставленный вопрос предполагает обращение к целям изучения темы «Первообразная и интеграл» в курсе математики средней школы и учет основного содержания этой темы. В качестве таких задач можно указать следующие:
- ввести понятия первообразной и интеграла;
- познакомить учащихся с основными свойствами первообразных и правилами нахождения первообразных (правилами интегрирования);
- раскрыть смысл операции интегрирования как операции, обратно по отношению к операции дифференцирования заданной функции;
- выделить типы задач (нахождение площади криволинейной трапеции, нахождение объема тела, задачи с физическим содержанием); показать, каким образом реализуется метод интегрального исчисления. При этом обратить внимание на выделение в процессе их решения этапов, характеризующих процесс математического моделирования.
2) Какой теоретический материал следует считать основным с учетом сформулированных выше целей и задач изучения темы «Первообразная и интеграл»?
В этот материал необходимо включить:
- понятие первообразной, основное свойство первообразной;
- понятие интеграла функции;
- связь между понятиям и «интеграл» и «первообразная», которая устанавливается с помощью формулы Ньютона-Лейбница;
- формула Ньютона-Лейбница как аппарат вычисления интеграла данной функции.
Каковы особенности изучения основного материала темы?
Ответ на этот вопрос предполагает раскрытие сущности рассматриваемых понятий; установление связей между вводимыми элементами материала и теми, которые уже изучены и помогают усвоению нового; выявление роли задач на этапах введения новых понятий, их применения, установления связей между введенными понятиям и и т.п. При этом естественно обратиться к изложению (или различным вариантам изложения, предложив их сравнительный анализ) материала темы в имеющихся в настоящее время учебных пособиях [5], [9], [13].
Предложим схемы ответов на поставленный вопрос, имея в виду указанные выше основные элементы материала темы.
3) Понятие первообразной, основное свойство первообразной.
Оба учебных пособия используют следующую схему изложения материала:
а) Создание установки на введение нового понятия и изучение свойств этого понятия. С этой целью внимание обращается на две взаимно обратные задачи: нахождение скорости и ускорения тела при свободном падении (к определенному моменту времени), если известен закон изменения пути; установление закона изменения скорости (пути), если задан закон изменения ускорения (скорости). Вторая задача формулируется в общем виде, а именно: дана производная некоторой функции, нужно на заданном промежутке найти саму функцию.
В связи с необходимостью решения этой задачи вводим новую операцию — интегрирование.
б) С операцией интегрирования (восстановления функции по ее производной) связаны:
- понятие первообразной;
- основное свойство первообразной;
- правила нахождения первообразных.
Указанные вопросы вводятся дедуктивно, дается иллюстрация использования определения основного понятия, его свойств с помощью конкретных примеров.
Задачи, помимо использования их как средства иллюстрации вводимого в рассмотрение теоретического материала, служат средством его закрепления. Об этом свидетельствуют и формулировки задач: «доказать, что функция F является первообразной для функции f на заданном промежутке», «Найти первообразную для данной функции на указанном промежутке», «Найти такую первообразную функции, график которой проходит через данную точку» и т.п.
К каким выводам приводит анализ материала учебных пособий, связанного с понятием «первообразная»?
Во-первых, учитель должен подготовить изучение темы: он должен четко представлять себе, что для этого нужно сделать, какой материал повторить, какие приемы целесообразно использовать.
Очевидно, целесообразно обратиться к
таблице производных изученных функций;
геометрическому и физическому смыслу производной;
правилам дифференцирования.
При этом можно использовать вопросы теоретического и практического содержания, специально подобранные задачи.
Во-вторых, введение понятия первообразной и изучение основного свойства первообразной полезно предварить работой с конкретными задачами.
Приведем примеры:
Задача 1. Тело движется
прямолинейно со скоростью ![]() . Найти закон
изменения пути в зависимости от времени.
. Найти закон
изменения пути в зависимости от времени.
Задача 2. Найти уравнение кривой, угловой
коэффициент касательной к которой в любой точке некоторого промежутка задается
следующим образом: ![]() .
.
В процессе решения этих задач внимание учащихся
обращается на связь данного и искомого (данная функция есть производная
искомой). В первом случае скорость движения тела в каждый момент времени
известна, она является производной соответствующего пути; значит, требуется
найти такую функцию, производная которой равна 2t. Во втором случае дана
формула, определяющая производную некоторой функции в каждой точке
фиксированного промежутка, а нужно найти функцию (производная функция равна ![]() );
);
Какие выводы следует сделать в результате анализа решений обеих задач?
- Решение состояло в нахождении функции по известной производной.
- Функций, которые удовлетворяют условиям предложенных задач, бесконечно много.
Таким образом, мы, с одной стороны, создали базу для введения понятия первообразной и операции интегрирования как обратной операции дифференцирования функции, а с другой, оказываемся в условиях целесообразности формулирования и доказательства теоремы, которая выражает основное свойство первообразной.
В-третьих, целесообразно обратить внимание учащихся на следующее: запись F(х)+C (общий вид первообразных для функции f(х) на заданном промежутке) связывает нас, с одной стороны, с произвольным значением постоянной С, а с другой, в зависимости от условия предложенной для решения задачи — с конкретным. С этой целью можно вернуться к анализу решений уже рассмотренных задач.
В первой из них в качестве искомой могла быть указана
, например, функция вида ![]() , во второй
—
, во второй
— ![]() (С —
некоторая постоянная). Чтобы показать, что учет конкретных условий задачи
влечет обращение к вполне определенной первообразной, можно предложить учащимся
найти уравнение пути, если за 2 с тело прошло 15 м (найти уравнение кривой,
проходящей через фиксированную точку А (1; 2)). Решение обеих задач
связано с нахождением тех первообразных заданных функций, которые удовлетворяют
указанным начальным условиям. Каждая из таких первообразных определяется
однозначно:
(С —
некоторая постоянная). Чтобы показать, что учет конкретных условий задачи
влечет обращение к вполне определенной первообразной, можно предложить учащимся
найти уравнение пути, если за 2 с тело прошло 15 м (найти уравнение кривой,
проходящей через фиксированную точку А (1; 2)). Решение обеих задач
связано с нахождением тех первообразных заданных функций, которые удовлетворяют
указанным начальным условиям. Каждая из таких первообразных определяется
однозначно: ![]()
Работа с задачами убеждает учащихся в том, что их решение связано с выделением из множества первообразных данной функции вполне определенных конкретных первообразных (именно с этим мы сталкиваемся при решении задач практического содержания).
Заметим, что обращение к указанным задачам дает возможность создать базу для раскрытия геометрического смысла основного свойства первообразной.
В-четвертых, изучение вопроса о правилах отыскания первообразных естественно связать с обращением к двум взаимнообратным операциям: дифференцированию и интегрированию.
Например, введение третьего правила (если F (х)
— первообразная для функции f (х), а ![]() и b — постоянные,
то
и b — постоянные,
то ![]() есть первообразная для функции
есть первообразная для функции ![]() ), можно предварить рассмотрением с
учащимися следующих задач:
), можно предварить рассмотрением с
учащимися следующих задач:
-
найти
производные функций ![]()
-
найти
хотя бы одну первообразную для функции ![]()
Анализ решений этих задач и приводит к формулировке указанного правила нахождения первообразных, доказательство которого можно предложить учащимся провести самостоятельно.
4. Введение понятия интеграла. Установление связи между понятиями «интеграл» и «первообразная».
Следует обратиться к схемам изложения материала, связанного с указанным вопросом, в учебном пособии [9] и пробном учебнике [5], и установить, в чем их отличие.
Учебное пособие [9] рассматривает:
1) Площадь криволинейной трапеции как приращение первообразной непрерывной функции, заданной на отрезке:
- понятие криволинейной трапеции;
-
теорема,
дающая один из подходов к задаче нахождения площади криволинейной трапеции (![]() где F — первообразная для
непрерывной, неотрицательной на отрезке [a; b] функции f);
где F — первообразная для
непрерывной, неотрицательной на отрезке [a; b] функции f);
- утверждение: любая непрерывная на данном промежутке функция имеет на нем первообразную.
2) Интеграл:
- второй подход к задаче нахождения площади криволинейной трапеции (фактически рассмотрение предела интегральных сумм);
-
понятие
интеграла как числа, к которому стремятся интегральные суммы (при ![]() );
);
- связь между интегралом непрерывной, неотрицательной на отрезке [a; b] функции и площадью соответствующей криволинейной трапеции.
3) Формулу Ньютона-Лейбница:
-
сравнение
результатов решения задачи о площади криволинейной трапеции при двух
рассмотренных подходах (вывод:  где F —
первообразная для непрерывной, неотрицательной на отрезке [a; b] функции
f);
где F —
первообразная для непрерывной, неотрицательной на отрезке [a; b] функции
f);
- вывод о справедливости полученной формулы для любой непрерывной на отрезке функции (без доказательства).
Изложение соответствующего материала в пробном учебнике [5] принципиально не отличается от изложения в пособии [9], хотя есть расхождения в последовательности рассмотрения отдельных вопросов. Схема изложения может быть условно представлена следующим образом: понятие криволинейной трапеции — площадь криволинейной трапеции как предел соответствующих интегральных сумм (площадь под графиком некоторой функции, заданной на отрезке) — интеграл от функции на отрезке как предел интегральных сумм — связь между интегралом непрерывной неотрицательной на отрезке функции и площадью криволинейной трапеции — получение формулы Ньютона-Лейбница, устанавливающей связь между интегралом и первообразной и позволяющей вычислить интеграл (так же, как и в пособии [9], формула Ньютона-Лейбница выводится на основе наглядных представлений в процессе решения задачи на нахождение площади криволинейной трапеции как приращения первообразной).
С рассматриваемым теоретическим материалом связаны два основных вида задач. Они, как правило, предлагаются в следующих формулировках: вычислить площадь фигуры, ограниченной линиями; вычислить интеграл.
Замечание. К понятию интеграла, как известно, приводит не только задача о площади криволинейной трапеции, но и другие задачи, например задача о работе силы, задача о количестве электричества, протекающем за данный промежуток времени через поперечное сечение проводника. С методикой использования этих задач для введения понятия «интеграл» можно познакомиться в книге [70].
Анализ материала учебных пособий, связанного с введением понятия «интеграл» и получением способа вычисления интегралов, приводит к ряду важных в методическом отношении выводов, которые полезно иметь в виду, разрабатывая методику изучения отдельных вопросов рассматриваемой темы. Что это за выводы?
Во-первых, определение интеграла и формула Ньютона-Лейбница дают возможность доказать ряд часто применяемых свойств интеграла. Понятно, что в процессе их доказательства понятие интеграла, его геометрический смысл будут глубже усваиваться учащимися. Можно предложить, например, установить справедливость следующих утверждений:

-
если
функция f имеет на отрезке [a; b] первообразную, то  (с — некоторая постоянная);
(с — некоторая постоянная);
-
если
функции ![]() и
и ![]() имеют на отрезке [a; b] первообразные,
то
имеют на отрезке [a; b] первообразные,
то 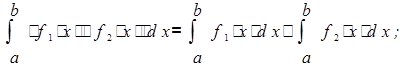
-
если
![]() то
то  (№ 455, [9]);
(№ 455, [9]);
-
доказать
формулу вычисления производной от интеграла с переменным верхним пределом
интегрирования  где f(х)
— функция, непрерывная на интервале, содержащем точки а и х (№
457, [9]).
где f(х)
— функция, непрерывная на интервале, содержащем точки а и х (№
457, [9]).
Предложенные упражнения полезны еще и потому, что в процессе их решения устанавливаются (и используются) связи между операциями дифференцирования и интегрирования, между понятиями «производная», «первообразная», «интеграл» и их свойствами.
Следует подумать о месте включения этих упражнений в учебный материал и методике работы с ними.
Во-вторых, понятие интеграла вводится для функции, непрерывной на некотором отрезке (такая функция имеет на этом отрезке первообразную). Сознательному усвоению учащимися этого понятия (и понятия первообразной) будет способствовать специальное привлечение внимания школьников к этому факту. С этой целью могут быть использованы задачи, например, такие:
Задача 1. Возможно ли
вычислить  (подынтегральная функция имеет
точку разрыва
(подынтегральная функция имеет
точку разрыва ![]() , принадлежащую отрезку
, принадлежащую отрезку ![]() )?
)?
Задача 2. Найти ошибку в вычислении интеграла
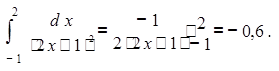
(О том, что ошибка действительно допущена, свидетельствует результат: интеграл от положительной функции оказался отрицательным числом.)
Задача 3. При каких значениях пределов интегрирования интеграл существует
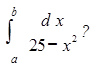
(В точках ![]() подынтегральная
функция терпит разрыв; поэтому можно говорить о следующих условиях, которым
должны удовлетворять значения пределов интегрирования:
подынтегральная
функция терпит разрыв; поэтому можно говорить о следующих условиях, которым
должны удовлетворять значения пределов интегрирования:
Задача 4. Вычислить:
а) 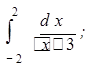 б)
б) 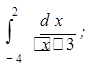 в)
в)  .
.
(В двух последних случаях интегралы не могут быть вычислены, так как подынтегральная функция не определена в каждой точке отрезка, заданного пределами интегрирования.)
В-третьих, установление связей между понятиям и «интеграл» и «первообразная» (точнее приращение первообразной) происходит через обращение к площади соответствующей криволинейной трапеции. Следовательно, значительное внимание при изучении материала нужно уделить геометрическому смыслу интеграла, не ограничиваясь при этом только использованием геометрических иллюстраций в процессе решения задач на вычисление интегралов.
Целесообразно специально подчеркнуть, что, опираясь на геометрический смысл интеграла, иногда получаем возможность
установить существование более простого по сравнению с рассмотренным способа вычисления интегралов (например, по симметричному относительно точки О промежутку от четной или нечетной функции). Сделать это можно, обратившись к задачам:
Задача 1. Показать, что
если f — непрерывная, четная на отрезке [-а; а] функция,
то 
Задача 2. Показать, что
если f — непрерывная, нечетная на отрезке [-а; а] функция,
то 
Задача 3. Вычислить:
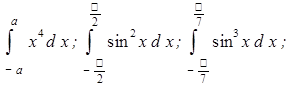
не только вычислять площади фигур, но и находить числовые значения интеграла, вычисление которых по известным учащимся формулам выполнить не удается.
Например:

Замечание. Можно предложить следующую схему введения понятия «интеграл»:
понятие криволинейной трапеции — площадь криволинейной трапеции как приращение первообразной соответствующей непрерывной функции, заданной на отрезке, - понятие интеграла (интеграл непрерывной функции на отрезке есть приращение первообразной для этой функции:
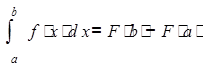 ).
).
В чем достоинства и недостатки предложенной схемы введения понятия «интеграл»? Возможно ли следовать ей при изучении материала соответствующей темы школьного курса математики? Как должно быть организовано в этом случае изучение материала?
5. Какова схема, отражающая связи между понятиям и, свойствами понятий темы «Первообразная и интеграл»?
Эту схему наглядно можно представить, например, следующим образом:
Анализ предложенной схемы убеждает в правомерности методических выводов, которые сделаны на основе обращения к материалу учебных пособий [5], [9], [13] и отражены в этом параграфе.
6. Обратимся к задачам, которые предложены учебными пособиям и [5] и [9] в теме «Первообразная и интеграл».
Можно ли утверждать, что, рассматривая с учащимися способы решения этих задач, организуя самостоятельную работу школьников с ними, мы реализуем основные цели изучения темы?
Ответ на этот вопрос предполагает выделение трех групп задач:
- задачи, которые непосредственно направлены на формирование понятий, использование свойств понятий, закрепление способов деятельности с введенными понятиям и (задачи, которые в большей мере несут дидактическую функцию);
- задачи, в результате решения которых получаем либо новый факт (он может быть полезен в будущем), либо новый способ решения задач определенного вида (познавательные задачи);
- задачи, в процессе решения которых формируются операции, приемы мышления, создаются предпосылки для осуществления творческой деятельности, в том числе и математической (задачи, основная функция которых развивающая).
Очевидно, что с группой общеобразовательных целей изучения темы в большей мере должна соотноситься группа задач с дидактическими функциями, ряд познавательных задач при определенных условиях тоже может быть использован для реализации указанных целей.
Воспитательная и развивающая цели изучения материала достигаются в процессе решения всех трех групп задач, но наибольшую значимость в данном случае имеют развивающие и познавательные задачи.
Ориентируясь на материал пособий [5], [9], следует отнести предлагаемые задачи к одной из указанных выше групп и указать, какова конкретная «нагрузка» отдельных задач или их серий.
7. Какими знаниями и умениями должны владеть учащиеся к моменту изучения темы «Первообразная и интеграл», какие знания, умения формируются в процессе изучения темы?
Ответ на указанный вопрос должен определяться программой по математике для средней школы, целями изучения темы, а также обязательными результатами, которые должны быть достигнуты всеми без исключения учащимися в результате работы с учебным материалом (обязательные результаты обучения учащихся по теме «Первообразная и интеграл» приведены в журнале «Математика в школе».- 1985.- № 4.- С. 28).
8. Выводы:
- понятие интеграла в курсе математики средней школы вводится на основе понятия предела соответствующих интегральных сумм;
- вычисление интегралов связано с использованием приращения соответствующих первообразных (формула Ньютона-Лейбница);
- площадь криволинейной трапеции является основным звеном, с помощью которого устанавливается связь между понятием интеграла функции и приращением соответствующей первообразной. Установление этой связи приводит и к способу (одному из возможных) вычисления интеграла;
- большое внимание в процессе изучения материала темы нужно уделить работе, связанной с разъяснением учащимся геометрического смысла интеграла и показом возможностей его использования для решения ряда конкретных задач.
Задания для самостоятельной работы
1. Ориентируясь на методические указания, приведенные в настоящих материалах, разработайте методику введения понятия «первообразная» и основного свойства первообразной.
Литература: [5], [9], [13], [70], [38].
2. Продумайте методику использования задач при введении понятия «интеграл» и установлении его свойств, связей с понятием «первообразная».
Литература: [61], [70], [74], [38].
3. Проанализируйте материалы контрольной работы по теме «Первообразная и интеграл» (см.: Математика в шк.- 1986.- 4.- С. 20; контрольная работа № 3) и соотнесите предложенные задания с заданиями соответствующего раздела «Обязательные результаты обучения» (см.: Математика в шк.- 1985.- № 4.- С. 28).
4. Познакомьтесь с примерным поурочным планированием материала темы «Первообразная и интеграл» (см.: Математика в шк.- 1986.- № 3.- С. 47).
II. Поурочное планирование изучения материала темы «Первообразная и интеграл»
Цель. Установить круг задач, в процессе решения которых находят применение понятие интеграла и способ вычисления интеграла конкретной функции; с учетом целей и задач темы, а также конкретного содержания учебника выполнить поурочное разбиение учебного материала.
План реализации второй части работы
1. Виды задач, для решения которых используется метод интегрального исчисления.
2. Составление подробного плана изучения материала темы «Первообразная и интеграл».
Основное содержание
1. Программа по математике не ставит цели научить школьников применять метод интегрального исчисления при решении задач; предполагается лишь знакомство с использованием метода, иллюстрация применения интеграла к решению задач.
Какие виды задач, в основе решения которых лежит метод интегрального исчисления, можно выделить? Какие из этих видов рассматриваются в процессе изучения темы?
для ответа на поставленные вопросы целесообразно обратиться к следующей литературе: [5], [9], [1], [13], [22], [64], [68], [70], [83].
Основной вид задач, при решении которых мы имеем возможность реализовать цели изучения темы, и особенно воспитательную и развивающую,- это задачи на нахождение площадей плоских фигур.
Следует продумать:
- каким образом реализуются в данном случае основные этапы решения прикладных задач средствами математики;
- как, имея в виду рассматриваемый вид задач, показать учащимся универсальность математических методов.
2. Составляя тематический план изучения вопросов, связанных с понятиями «первообразная», «интеграл», нужно особое внимание уделить:
- формулированию цели, конкретных задач каждого урока;
- обоснованию отбора учебного материала на урок (как теоретического, так и набора задач);
- четкому указанию тех конкретных связей, которые должны установиться между элементами нового и уже изученного материала (внутрипредметные связи), между элементами материала данного предмета и других предметов, например физики (межпредметные связи).
Задание для самостоятельной работы
Закончите составление плана изучения со школьниками материала темы «Первообразная и интеграл».
Литература: [5], [9], [13], [22], [64], [61], [68], [70], [74], [83], [96], [125].
§ 10. МЕТОДИКА И3УЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
В КУРСЕ АЛГЕБРЫ И НАЧАЛ АНАЛИ3А
План
1. Образовательные, воспитательные и развивающие цели изучения тригонометрических функций в Х классе.
2. Содержание учебного материала, связанного с изучением тригонометрических функций в курсе алгебры и начал анализа.
3. Выполнение практических заданий, связанных с разработкой отдельных методических вопросов изучения тригонометрических функций в Х классе.
При разработке методики . изучения этой темы необходимо поставить следующие цели:
1. Разработать один из вариантов введения понятия тригонометрических функций числового аргумента. 2. Проанализировать набор задач, направленных на формирование понятия о периодичности тригонометрических функций.
Задания, предваряющие занятия по указанной теме
1. Выделить ключевые вопросы развертывания функциональной линии в школьном курсе математики и указать класс, в котором рассматривается соответствующий вопрос (на основе анализа учебников алгебры, алгебры и начал анализа).
2. Указать основные этапы введения понятия о тригонометрических функциях числового аргумента (на основе анализа учебников геометрии, алгебры, алгебры и начал анализа).
3. Познакомиться с требованиями программы по изучению тригонометрических функций в Х-ХI классах (см.: Математика в шк.- 1985.- № 6.- С. 12-13).
4. Установить, какие свойства тригонометрических функций рассматриваются в Х-ХI классах.
Основное содержание
1. Основные образовательные цели изучения тригонометрических функций в курсе алгебры и начал анализа могут быть сформулированы исходя из характерной особенности курса, выделенной в программе по математике.
Характерной особенностью курса является систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков, полученных в курсе алгебры, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения (см.: Математика в шк.- 1985.- № 6.- С. 12).
Основные образовательные цели изучения тригонометрических функций в Х классе:
1) систематизировать знания учащихся о тригонометрических функциях числового аргумента;
2) обобщить и расширить знания о свойствах тригонометрических функций;
3) закрепить и развить умения проводить тождественные преобразования тригонометрических выражений, используя формулы, указанные в программе.
4) познакомить с решением простейших тригонометрических уравнений и неравенств, а также рассмотреть некоторые приемы решения тригонометрических уравнений и их систем.
2. Анализ учебного материала курса алгебры и начал анализа позволяет выделить следующее основное содержание:
- радианная система измерения углов;
- определение синуса, косинуса, тангенса и котангенса углов, измеренных в радианной системе измерения;
- определение тригонометрических функций числового аргумента;
- свойства тригонометрических функций (четность и периодичность), существенные для построения графиков функций, и построение графиков тригонометрических функций;
(Заметим, что перечисленные выше элементы содержания, за исключением графиков функций, в Х классе лишь актуализируются. Они ранее рассматривались в курсе алгебры IX класса.)
- основные тригонометрические формулы и их использование для выполнения тождественных преобразований тригонометрических выражений;
- на базе основных свойств функций исследуются тригонометрические функции, при этом отдельно изучается характеристическое свойство тригонометрических функций — периодичность;
- обратные тригонометрические функции;
- решение простейших тригонометрических уравнений и неравенств;
- приемы решения некоторых видов тригонометрических уравнений и их систем;
- производные тригонометрических функций;
-
функция
вида ![]() , описывающая гармонические колебания.
, описывающая гармонические колебания.
Анализ содержания учебного материала показывает, что среди перечисленных вопросов наиболее существенное значение имеют:
- определение тригонометрических функций числового аргумента;
- характеристическое свойство тригонометрических функций — периодичность;
- обратные тригонометрические функции и использование их для решения простейших тригонометрических уравнений и неравенств.
Остановимся на подробном рассмотрении первых двух вопросов.
Оба они важны для понимания особенностей тригонометрических функций по сравнению с ранее изученными учащимися функциями.
3. Тригонометрические функции являются первым примером трансцендентных функций, рассматриваемых в школе. При первоначальном введении этих функций они рассматриваются как функции угла. Другими словами, аргументом этих функций служит геометрический объект. Однако как потребности самой математики, так и ее приложений требуют рассмотрения тригонометрических функций числового аргумента.
Наиболее полно раскрывается понятие о тригонометрических функциях числового аргумента в IX классе.
На занятии выделяются основные этапы введения понятия
о тригонометрических функциях числового аргумента на примере функции ![]() и формулируются ведущие методические
положения, на которых основано конкретное изучение данного вопроса.
и формулируются ведущие методические
положения, на которых основано конкретное изучение данного вопроса.
Этапы:
Исходя из особенностей этапа формирования понятия о
тригонометрических функциях числового аргумента формулируем цель изучения
указанного понятия в Х классе: повторение известных из IX класса сведений о
тригонометрических функциях числового аргумента с целью выделения всех
существенных признаков понятия; знакомство с графиками тригонометрических
функций (![]() ).
).
Работа по выделению существенных признаков понятия «тригонометрические функции числового аргумента» может быть построена двумя путями:
а) анализ текста учебника ([4], § 1, п. 1) и последовательное выделение и определение «методической нагрузки» отдельных отрезков текста;
б) анализ термина «тригонометрические функции числового аргумента» и получение существенных признаков на основе этого анализа.
Второй путь кажется более плодотворным. Он предполагает актуализацию понятий
«числовые функции» и «тригонометрические функции углового аргумента»,
а также сравнение этих понятий.
В результате сравнения усматривается, что при рассмотрении тригонометрических функций углу сопоставляется число, в то время как при рассмотрении ранее известных функций (числовых) числу сопоставлялось число.
Поскольку для исследования тригонометрических функций и построения графиков необходимо пользоваться общими приемами, известными для числовых функций, то целесообразно (если это возможно) рассматривать тригонометрические функции числового аргумента.
Далее устанавливается возможность перехода от углового к числовому аргументу при рассмотрении тригонометрических функций и роль при этом радианного измерения углов.
Идею сопоставления каждому действительному числу
значения тригонометрической функции (например, ![]() ) целесообразно
проиллюстрировать на модели (рис. 27).
) целесообразно
проиллюстрировать на модели (рис. 27).
Заметим, что рисунок 28 иллюстрирует идею наматывания числовой оси на единичную окружность.
При рассмотрении модели необходимо обратить внимание,
что в качестве единицы (единичного отрезка) по оси ![]() выбирается один радиан (длина
соответствующей дуги).
выбирается один радиан (длина
соответствующей дуги).
Требует дополнительного обоснования и тот факт, что ![]() является функцией с областью определения
и областью значении [-1; 1].
является функцией с областью определения
и областью значении [-1; 1].
После такого обзора содержания предлагается представить свой вариант рассмотрения в Х классе понятия о тригонометрических функциях числового аргумента. Он обсуждается с точки зрения обеспечения глубины усвоения формируемого понятия.
Второй вопрос, который целесообразно рассмотреть в связи с изучением тригонометрических функций в Х классе, — это вопрос о свойствах этих функций.
После перечисления всех свойств из набора, рассматриваемого в школе, необходимо более подробно остановиться на методике изучения свойства, характеристического для тригонометрических функций, — периодичности.
В ходе обсуждения можно остановиться на следующих вопросах:
1) Пропедевтика понятия о периодичности функции (IX-Х классы).
2) Использование свойства периодичности при знакомстве с построением графиков тригонометрических функций.
3) Анализ определения понятия «периодическая функция».
4) Аналитическая и геометрическая интерпретации периодической функции.
5) Период и наименьший положительный период функции.
Для введения общих формул решения простейших
тригонометрических уравнений и неравенств при рассмотрении тригонометрических
функций в Х классе вводятся понятия «арксинус», «арккосинус», «арктангенс» и «арккотангенс
числа а». Каждое из этих понятий вводится как число — корень
соответствующего уравнения (![]() ) - на
определенном интервале. Вопрос о существовании и единственности такого числа
решается на основе рассмотрения теоремы о корне.
) - на
определенном интервале. Вопрос о существовании и единственности такого числа
решается на основе рассмотрения теоремы о корне.
Целесообразно подробно рассмотреть доказательство указанной выше теоремы о корне ([9], с. 44) и введение, например, понятия арксинуса а.
В заключение анализа пункта 10 учебника [9] ответьте на вопрос: вводится ли в тексте учебника (явно или неявно) понятие об обратных тригонометрических функциях? Повторите основные сведения об обратных тригонометрических функциях (определения, свойства, графики).
Существенное внимание необходимо уделить анализу задач, помещенных после пункта учебника, в котором рассматривается свойство периодичности тригонометрических функций.
В ходе анализа системы математических задач
выделите задачи (группы задач) на отработку определенного элемента теории, представленного в тексте учебника;
выделите математические задачи, связанные с формированием практических умений;
оцените представленный в учебнике набор задач с точки зрения формирования исследовательских умений учащихся;
определите возможности дополнения представленного набора задач (учитывая рассмотренный теоретический материал).
4. Выводы:
- понятие о тригонометрических функциях числового аргумента рассматривается в Х классе на основе повторения известных учащимся сведений из курса алгебры IX класса;
- в Х классе важно выделить все существенные признаки понятия «тригонометрические функции числового аргумента» исходя из двух понятий: «числовая функция» и «тригонометрическая функция углового аргумента»;
- при рассмотрении понятия «тригонометрические функции числового аргумента» важно сделать актуально осознаваемой учащимися идею соответствия каждому действительному числу (значению аргумента) другого действительного числа (значения тригонометрической функции);
- использовать определение тригонометрической функции числового аргумента и известные свойства этих функций для построения графиков;
- отработать существенные признаки понятия «периодическая функция» в ходе решения задач;с этой целью (и на основе анализа набора задач учебника) составить систему задач.
Самостоятельная работа
1. Выделите прием решения задачи № 86 из [9] и оформите его в виде алгоритмического предписания.
2. Предложите методический подход для работы с задачами типа № 87-89 из [9].
3. Составьте серию задач на распознавание периодических функций при графическом способе их задания.
4. Подготовьте методическую разработку по введению
понятия о тригонометрических функциях числового аргумента (на примере функций ![]() ).
).
Индивидуальное задание
Выполните сравнительный анализ введения понятия тригонометрических функций числового аргумента по разным учебникам.
Литература: [9], [8], [5], [37].
§ 11. ЛОГИКО-ДИДАКТИЧЕСКИЙ АНАЛИЗ ЛИНИИ УРАВНЕНИЯ
В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ
В школьном курсе математики можно проследить несколько математических линии, которые из класса в класс получают развитие, углубление и конкретизацию. Одним из профессиональных умений учителя будет умение устанавливать содержательные связи по реализации линий между материалом разных классов. Учитель должен знать специфику доказательств (обоснований) действий и операций в зависимости от класса, в котором изучается определенная часть учебного материала, уметь оформить изучаемый материал и решение математических задач в зависимости от места его изучения в школе. Это одно из сложных методических умений, и приходит оно с опытом работы в школе. Но первое приобщение к данному умению необходимо осуществить в вузе на примере 2-3 линий. Чтобы поставить методические задачи, связанные с осмыслением реализации той или иной математической линии, необходимо проанализировать учебники и отобрать «ядерный» материал линии, его логическую организацию, математические трактовки и связи с другими предметами.
На примере линии уравнений покажем результаты анализа, оформив их в таблицу (табл. 20). По математической линии можно поставить ряд познавательных и методических задач.
Задача 1. Выясните различия в математическом обосновании решения уравнений в V и VI классах.
3адача 2. На какой логической и математической основе решаются линейные и квадратные уравнения в школе?
3адача 3. С какими (логическими или алгебраическими) преобразованиями связана потеря корней уравнения? Разработайте наборы задач для предупреждения ошибки — потеря корня.
3адача 4. На основе анализа содержания учебного материала определите специфические действия по формированию понятия квадратного уравнения с целью сознательного усвоения и применения формул корней квадратного уравнения.
3адача 5. Проанализируйте математические задачи по теме «Решение иррациональных уравнений» и выясните математические и учебные действия, используемые для их решения. Разработайте методику обучения поиску решения иррациональных уравнений.
3адача 6. Укажите логические и
функциональные обоснования, лежащие в основе решения трансцендентных уравнений
(![]() и
и ![]() ).
).
Предложите методику введения этих обоснований в школе.
Разработайте систему наглядности для установления
связи между областями определения и значений прямой и обратной функций ![]() , обоснованиями решения трансцендентных
уравнений.
, обоснованиями решения трансцендентных
уравнений.
Литература: [2] — [9], [36] — [38], [94], [95], [107], [108], [131].
Таблица 20
Анализ линии уравнений в курсе математики средней школы
|
Класс |
Тема |
Содержание, основное понятие, факт |
Обоснование решений уравнений |
Опорные знания |
Приложение |
|
|
в математике |
в смежных дисциплинах |
|||||
|
V |
Натуральные числа и действия над ними
Проценты |
Понятие об уравнении. Нахождение неизвестного компонента действия
Понятия о дроби, форме записи дроби, проценте |
На основе зависимости между компонентами и результатами действий
-»- |
Зависимость между компонентами и результатами действий. Взаимосвязь между величинами (знания по природоведению из начальных классов) Десятичные дроби, запись десятичной дроби. Основное свойство дроби |
Решение сюжетных задач
Решение сюжетных задач на проценты с помощью уравнений |
Природоведение — климат Трудовое обучение — различные расчеты
Природоведение — цифровой материал о составе атмосферы, компонентов состава почвы и др. |
|
VI |
Арифметические действия над обыкновенными дробями
Пропорции
Линейные уравнения с одним неизвестным |
Решение простейших линейных уравнений, свойства действий над обыкновенными дробями. Нахождение неизвестного компонента действия Составление и решение простейших уравнений; отношение, равенство отношений, пропорция, свойство пропорции
Понятие об уравнении, решение уравнения на основе свойств равенств, приведение подобных членов, составление и решение уравнений |
-»-
-»-
На основе свойств равенств и определений понятий «модуль числа» и «степень» |
Основное свойство дроби. Законы арифметических действий. Возникновение дробей
Взаимосвязь между величинами. Основное свойство дроби
Действия над рациональными числами, приведение подобных членов, свойства равенств |
Решение сюжетных задач с помощью уравнений, нахождение дроби числа и числа по его дроби Решение сюжетных задач составлением уравнения с использованием понятия пропорции Решение сюжетных задач составлением уравнений |
География — формы поверхности суши Трудовое обучение — расчеты
Трудовое обучение — расчетные таблицы География — масштаб
География — составление простейших математических моделей явлений Трудовое обучение — расчетные таблицы |
|
VII |
Линейные уравнения |
Понятия о линейном уравнении; о решении линейного уравнения с двумя неизвестными, о системе двух уравнений с двумя неизвестными, о графике линейного уравнения с двумя неизвестными. Геометрическая интерпретация линейного уравнения с двумя неизвестными, способы решения системы двух уравнений с двумя неизвестными |
На основе алгебраических преобразований и свойств равенств |
Решение линейного уравнения с одним неизвестным. Координатная плоскость. График уравнения. Принадлежность и непринадлежность точек графику |
Решение сюжетных задач на составление систем линейных уравнений с двумя неизвестными |
Физика — плотность, сила тяжести, равномерное движение и др. География — шкалы, графики |
|
VIII |
Квадратные уравнения
Рациональные уравнения |
Понятия о квадратном уравнении, о видах квадратных уравнений, о формулах корней квадратного уравнения. Теорема Виета. Система двух уравнений с двумя неизвестными выше первой степени, Способы решения таких систем Понятия о дробно-рациональном уравнении, о постороннем корне, о проверке корней. Способы решения дробно-рационального уравнения |
На основе тождественных преобразований и свойств равенств
На основе тождественных преобразований |
Корень уравнения. решение системы, арифметический корень, извлечение корня, формулы сокращенного умножения, тождественные преобразования рациональных выражений
Свойство алгебраических дробей, тождественные преобразования дробно-рациональных выражений |
Решение сюжетных задач, исследование функций элементарными средствами
Решение сюжетных задач. Связь с геометрией. Построение математических моделей |
Физика — давление в жидкости и газе, работа, мощность География — вопросы экономики Химия — расчеты в лабораторных работах |
|
IX |
Решение уравнений и неравенств |
Понятие о равносильности уравнений. Неравенство второй степени с одним неизвестным. Решение дробно-рациональных неравенств методом интервалов и замены неизвестных |
На основе тождественных преобразований и понятий равносильности уравнений |
Свойства квадратичной функции, свойства ранее изученных функций, корень уравнения, решение неравенств |
Исследование функции элементарными средствами. Решение сюжетных задач на арифметическую и геометрическую прогрессии |
Физика — электромагнитные явления, давление жидкости и газа, работа и мощность |
|
X |
Тригонометрические уравнения |
Понятие о тригонометрическом уравнении, о решении простейших уравнений (неравенств). Способы решения уравнений. Приближенное решение уравнений |
На основе понятий тригонометрической функции, основных тригонометрических тождеств, тождественных преобразований. Понятие о равносильности уравнений |
Свойства тригонометрических функций, метод интервалов. Основные тригонометрические тождества, понятие о равносильности уравнений |
Решение треугольников, приложение тригонометрии к геометрии. Нахождение расстояния в пространстве. Вычисления на микрокалькуляторе |
Информатика — составление алгоритмов Физика — механические колебания. Угловая и линейная скорости |
|
XI |
Степень с рациональным показателем
Показательная и логарифмическая функции |
Корень степени и его свойства. Решение простейших уравнений. Понятие об иррациональном уравнении, виды уравнений и способы их решения Понятие о показательном и логарифмическом уравнениях. Виды уравнений. Способы решения показательных и логарифмических уравнений |
На основе тождественных преобразований иррациональных выражений, понятия равносильности уравнений На основе определения функции, действий со степенями, тождественных преобразований, понятий равносильности |
Свойства изучаемых функций, корень уравнения, равносильность уравнений, свойства степени с рациональным показателем Свойства степеней, свойства показательной и логарифмической функций, равносильность уравнений |
Определение степени с произвольным показателем. Вычисления на микрокалькуляторе Вычисления на микрокалькуляторе |
Физика — электростатика Химия — расчеты реакций
Физика — элементы квантовой механики Биология — распространение популяций |
Рекомендуемая литература
ОГЛАВЛЕНИЕ
Глава I. Деятельность учителя математики и практическая система ее организации..............5
§ 1. Основные профессиональные умения учителя математики...............................................................-
§ 2. Цели и система проведения лабораторных и практических работ при формировании профессиональных умений учителя математики......................................................................................12
§ 3. Математические, учебные и методические задачи............................................................................22
Глава II. Лабораторные работы по методике преподавания математики...................................34
§ 4. Основные компоненты содержания учебного материала по математике в школе и их логико-математический анализ..................................................................................................................................-
§ 5. Лабораторные работы по логико-математическому анализу основных компонентов учебного материала.......................................................................................................................................................37
§ 6. Лабораторные работы по организационным вопросам обучения математике................................78
§ 7. Лабораторные работы, раскрывающие методические особенности обучения математическим методам в школе.........................................................................................................................................114
Глава III. Практические работы по методике преподавания математики................................166
§ 8. Логико-дидактический анализ темы......................................................................................................-
§ 9. Методика изучения темы «Первообразная и интеграл» в курсе алгебры и начал анализа.........190
§ 10 Методика изучения тригонометрических функций в курсе алгебры и начал анализа................203
§ 11 Логико-дидактический анализ линии уравнений в школьном курсе математики...............................209
Рекомендуемая литература........................................................................................................................214
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.