Колебания

К о л е б а н и я

 Уравнение колебательного движения  можно получить из аналогии вращательного и колебательного движений.

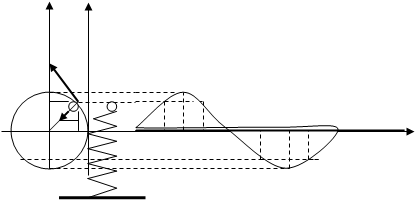                      y

                 V

Проекцию точки А на ось Х можно определить как   R× Cos  φ, где  φ = ×t. Следовательно,  уравнение движения можно записать  x = R× Cos t, где R - наибольшее отклонение от положения равновесия – амплитуда колебаний. Вектор скорости v направлен по касательной к окружности, а вектор а ускорения – по радиусу.  Учитывая направление вектора скорости и то, что линейная скорость определяется  как    v = , получим   v = - R× Sin t. Для ускорения соответственно  а = ² R   и   a = -²R ×Cos t . Знак «минус» свидетельствует о том, что направления векторов  v и a  противоположны направлению х.

 Так как гармонические колебания происходят при действии силы, пропорциональной смещению, подчиняющейся закону Гука, запишем закон сохранения энергии  . Но  v = R , имеем   k x² = m ² x², откуда ²=    или,  так как   =     имеем       Т = 2 π .

                 В Е Л И Ч И Н Ы

Смещение – отклонение    x = f(t)     Мгновенное перемещение относительно                                                                y = f(t)      положения равновесия

Амплитуда  x_m , y_m  - максимальное отклонение, размах колебаний
         Период    длительность полного колебания
         частота     число колебаний в единицу времени
         угловая частота  w = 2 π f  = - число колебаний за 2π секунд.

Фаза  φ  = w t + φ_o     Начальная фаза  φ_o – начало колебаний, значение фазы при t = 0  Время отсчитывается от момента начала колебаний

Пример: Во сколько раз изменится период колебаний железного шарика, привязанного  к длинной нити, при погружении его в воду? Сопротивление воды не учитывать.

В воздухе Т₁ = 2π  в воде  Т₂ = 2π , где 

Следовательно 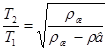 =  = 1,07 раз.

Задачи для самостоятельного решения

1.              В неподвижном лифте период колебаний математического маятника 1 с. С каким ускорением стал двигаться лифт, если период колебаний маятника стал 1,1 с?

2.              Найти период колебаний маятника длиной l м в вагоне поезда, едущего с ускорением а.

3.              В однородном электрическом поле на тонкой нити, длиной 35 см, подвешена материальная точка массой 15 г с зарядом 3,0 10^-6 Кл. Найти период собственных колебаний точки, если напряженность электрического поля          4.0 10⁴ В/м.

4.              Период  колебаний железного шарика массой 10г, привязанного к длинной нити 1,1 с. Когда снизу поставили магнит, период колебаний уменьшился до 1с. Определить силу притяжения магнита.

5.              Ведро, имеющее массу m и сечение S, совершает гармонические колебания малой амплитуды А_о. Начинает идти вертикальный дождь поверхностной плотностью μ (μ – масса воды, приносимая на единицу поверхности в единицу времени). Скорость U падения капель велика по сравнению с максимальной скоростью движения ведра. Определите зависимость координаты колебательного движения ведра от времени для случаев: а) ведро висит на длинной нити ( l >> A_o);  в) ведро висит на пружине жесткостью k и совершает колебания в вертикальной плоскости