Частное учреждение

профессиональная образовательная организация

ТЕХНИКУМ «БИЗНЕС И ПРАВО»

 

 

 

	Рассмотрено На заседании цикловой комиссии общеобразовательных и гуманитарных дисциплин Протокол № 1 «29» августа 2022г. Председател комиссии Назаров С.С.. _________		Утверждаю Заместитель директора по учебной работе   ___________ Н.В. Бакуменко                              «29» августа 2022г

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Комплект контрольно-оценочных средств

для оценки результатов освоения  дисциплины

ЕН.01 Математика

 

Программы подготовки специалистов среднего звена

44.02.02 Преподавание в начальных классах

 

 

 

 

 

 

 

 

 

 

Белореченск 2022г.

Комплект контрольно-оценочных средств разработан на основе рабочей программы учебной дисциплины ЕН.01 Математика, разработанной в соответствии с Программой подготовки специалистов среднего звена по специальности 44.02.01Дошкольное образование, 44.02.01 Преподавание в начальных классах базовой подготовки, введенной за счет часов вариативной части ФГОС.

 

 

 

 

Разработчик:

 

Косяченко А.Н. – преподаватель ЧУПОО ТЕХНИКУМ «БИЗНЕС И ПРАВО»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СОДЕРЖАНИЕ

 

1. Паспорт комплекта оценочных средств

     1.1 Область применения комплекта оценочных средств

     1.2 Результаты освоения учебной дисциплины, подлежащие проверке

2. Оценка освоения учебной дисциплины

     2.1 Формы и методы оценивания

3. Контрольно- оценочные средства

3.1Задания для проведения входного контроля

      3.2Задания для текущего контроля

      3.3 Задания для проведения промежуточной  аттестации по дисциплине

      3.4Пакет экзаменатора

 

 

1.      ПАСПОРТ КОМПЛЕКТА КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ

1.1    Область применения комплекта оценочных средств

           

Контрольно-оценочные средства (КОС) предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины ЕН.01Математика.

КОС включают контрольные материалы для проведения входного, текущего контроля и промежуточной аттестации в форме дифференцированного зачета.

Контрольно-оценочные средства разработаны в соответствии с документами:

·         ФГОС СПО 44.02.01 Дошкольное образование, 44.02.01 Преподавание в начальных классах;

·         Учебным планом и программой подготовки специалистов среднего звена специальности СПО 44.02.01 Дошкольное образование, 44.02.01 Преподавание в начальных классах;

·         программой учебной дисциплины ЕН.01 Математика.

1.2 Результаты освоения учебной дисциплины, подлежащие проверке

В результате аттестации по учебной дисциплине осуществляется комплексная проверка следующих умений и знаний:

Таблица 1

 

 

 

 

 

2.      ОЦЕНКА ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

2.1    Формы и методы оценивания

Предметом оценки служат умения и знания, предусмотренные ФГОС по дисциплине ЕН.01 Математика, направленные на формирование общих и профессиональных компетенций.

Элемент учебной дисциплины	Формы и методы контроля
	Текущий контроль		Промежуточная аттестация		Входной контроль
	Форма контроля	Проверяемые   У, З	Форма контроля	Проверяемые   У, З	Форма контроля	Проверяемые   У, З
Раздел 1.  Элементы логики	Устный опрос Письменные задания Практические работы №1-4 Самостоятельная работа	У1, У2У4, З1, З6, З10	Дифференцированный зачет	У1,У2,У3,У4 З1,З2,З3,З4,З5, З6,З7,З8,З9	Провероч ная работа	У1,У2, У3,У4 З1,З2,З3, З4,З5,З6, З7,З8,З9
Раздел 2.  Натуральные числа и нуль	Устный опрос Письменные задания Практические работы №5-10 Самостоятельная работа	У1, У3, З2, З3,З4,З5, З9
Раздел 3. Геометрические фигуры	Устный опрос Письменные задания Практические работы №11-14 Самостоятельная работа	У1, З7, З8

Контроль и оценка освоения учебной дисциплины по темам (разделам) Таблица 2

3.      КОНТРОЛЬНО-ОЦЕНОЧНЫЕМАТЕРИАЛЫ

3.1    Задания для проведения текущего контроля

 

Текущий контроль освоения обучающимися дисциплины ЕН. 02 Математика осуществляется преподавателем в процессе проведения практических занятий, устного и письменного опроса различных форм, а также выполнения обучающимися индивидуальных заданий, проектов, исследований и др. Задания для текущего контроля представлены в соответствии с логической последовательностью, выстроенной в рабочей программе дисциплины и календарно-тематическом плане.

 

3.2  Задания для проведения входного контроля

 

ВХОДНОЙ КОНТРОЛЬ:

 

Оцениваемые знания: остаточные знания по дисциплине.

Инструкция:

Внимательно прочитайте и решите задание.

Максимальное время выполнения задания –  45 мин.

                                                              

Вариант № 1

1. B 1 № 77346. Мо­биль­ный те­ле­фон стоил 3500 руб­лей. Через не­ко­то­рое время цену на эту мо­дель сни­зи­ли до 2800 руб­лей. На сколь­ко про­цен­тов была сни­же­на цена?

 

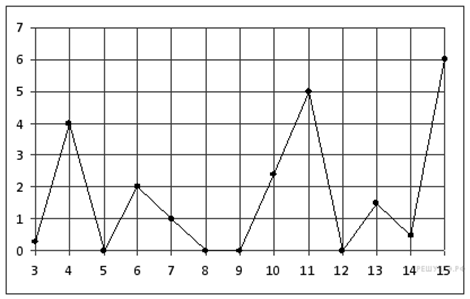
2. B 2 № 27523. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­но су­точ­ное ко­ли­че­ство осад­ков, вы­па­дав­ших в Ка­за­ни с 3 по 15 фев­ра­ля 1909 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство осад­ков, вы­пав­ших в со­от­вет­ству­ю­щий день, в мил­ли­мет­рах. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, сколь­ко дней из дан­но­го пе­ри­о­да не вы­па­да­ло осад­ков.

 

3. B 3 № 246381.

Вася за­гру­жа­ет на свой ком­пью­тер из Ин­тер­не­та файл раз­ме­ром 30 Мб за 29 се­кунд. Петя за­гру­жа­ет файл раз­ме­ром 28 Мб за 26 се­кунд, а Миша за­гру­жа­ет файл раз­ме­ром 32 Мб за 29 се­кунд. Сколь­ко се­кунд будет за­гру­жать­ся файл раз­ме­ром 496 Мб на ком­пью­тер с наи­боль­шей ско­ро­стью за­груз­ки?

4. B 4 № 58749. Пря­мая a про­хо­дит через точки с ко­ор­ди­на­та­ми (0; 2) и (2; 0). Пря­мая b про­хо­дит через точку с ко­ор­ди­на­та­ми (0; 4) и па­рал­лель­на пря­мой a. Най­ди­те абс­цис­су точки пе­ре­се­че­ния пря­мой b с осью Ox.

5. B 5 № 1007. Маша вклю­ча­ет те­ле­ви­зор. Те­ле­ви­зор вклю­ча­ет­ся на слу­чай­ном ка­на­ле. В это время по трем ка­на­лам из трид­ца­ти по­ка­зы­ва­ют те­ле­вик­то­ри­ны. Най­ди­те ве­ро­ят­ность того, что Маша по­па­дет на канал, где те­ле­вик­то­ри­ны не идут.

6. B 6 № 77373. Ре­ши­те урав­не­ние .

7. B 7 № 29575. 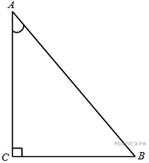В тре­уголь­ни­ке  угол  равен 90°, , . Най­ди­те .

8. B 10 № 26859. Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 54799.

Ко­эф­фи­ци­ент по­лез­но­го дей­ствия (КПД) не­ко­то­ро­го дви­га­те­ля опре­де­ля­ет­ся фор­му­лой , где  — тем­пе­ра­ту­ра на­гре­ва­те­ля (в гра­ду­сах Кель­ви­на),  — тем­пе­ра­ту­ра хо­ло­диль­ни­ка (в гра­ду­сах Кель­ви­на). При какой ми­ни­маль­ной тем­пе­ра­ту­ре на­гре­ва­те­ля  КПД этого дви­га­те­ля будет не мень­ше , если тем­пе­ра­ту­ра хо­ло­диль­ни­ка  К? Ответ вы­ра­зи­те в гра­ду­сах Кель­ви­на.

10. B 13 № 39257. Ве­ло­си­пе­дист вы­ехал с по­сто­ян­ной ско­ро­стью из го­ро­да А в город В, рас­сто­я­ние между ко­то­ры­ми равно 154 км. На сле­ду­ю­щий день он от­пра­вил­ся об­рат­но со ско­ро­стью на 3 км/ч боль­ше преж­ней. По до­ро­ге он сде­лал оста­нов­ку на 3 часа. В ре­зуль­та­те он за­тра­тил на об­рат­ный путь столь­ко же вре­ме­ни, сколь­ко на путь из А в В. Най­ди­те ско­рость ве­ло­си­пе­ди­ста на пути из А в В. Ответ дайте в км/ч.

11. B 14 № 245184. Най­ди­те наи­боль­шее зна­че­ние функ­ции 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 2

1. B 1 № 80181.

Пачка сли­воч­но­го масла стоит 66 руб­лей. Пен­си­о­не­рам ма­га­зин де­ла­ет скид­ку 5%. Сколь­ко руб­лей за­пла­тит пен­си­о­нер за пачку масла?

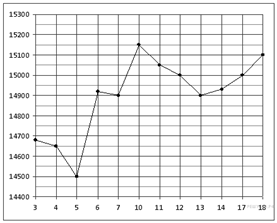
2. B 2 № 26875. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена олова на мо­мент за­кры­тия бир­же­вых тор­гов во все ра­бо­чие дни с 3 по 18 сен­тяб­ря 2007 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена тонны олова в дол­ла­рах США. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, ка­ко­го числа цена олова на мо­мент за­кры­тия тор­гов была наи­боль­шей за дан­ный пе­ри­од.

 

 

3. B 3 № 5551. Те­ле­фон­ная ком­па­ния предо­став­ля­ет на выбор три та­риф­ных плана.

 

 

Або­нент вы­брал наи­бо­лее де­ше­вый та­риф­ный план, ис­хо­дя из пред­по­ло­же­ния, что общая дли­тель­ность те­ле­фон­ных раз­го­во­ров со­став­ля­ет 600 минут в месяц. Какую сумму он дол­жен за­пла­тить за месяц, если общая дли­тель­ность раз­го­во­ров в этом ме­ся­це дей­стви­тель­но будет равна 600 минут? Ответ дайте в руб­лях.

4. B 4 № 244995. Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

5. B 5 № 320184. Иг­раль­ный кубик бро­са­ют два­жды. Сколь­ко эле­мен­тар­ных ис­хо­дов опыта бла­го­при­ят­ству­ют со­бы­тию «А = сумма очков равна 5»?

6. B 6 № 26651. Най­ди­те ко­рень урав­не­ния .

7. B 7 № 27305. 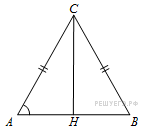В тре­уголь­ни­ке  , вы­со­та  равна 7, . Най­ди­те .

8. B 10 № 69155.

Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 41691.

Де­та­лью не­ко­то­ро­го при­бо­ра яв­ля­ет­ся вра­ща­ю­ща­я­ся ка­туш­ка. Она со­сто­ит из трeх од­но­род­ных со­ос­ных ци­лин­дров: цен­траль­но­го мас­сой  кг и ра­ди­у­са  см, и двух бо­ко­вых с мас­са­ми  кг и с ра­ди­у­са­ми . При этом мо­мент инер­ции ка­туш­ки от­но­си­тель­но оси вра­ще­ния, вы­ра­жа­е­мый в , даeтся фор­му­лой . При каком мак­си­маль­ном зна­че­нии  мо­мент инер­ции ка­туш­ки не пре­вы­ша­ет пре­дель­но­го зна­че­ния ? Ответ вы­ра­зи­те в сан­ти­мет­рах.

10. B 13 № 26593. Заказ на 156 де­та­лей пер­вый ра­бо­чий вы­пол­ня­ет на 1 час быст­рее, чем вто­рой. Сколь­ко де­та­лей в час де­ла­ет пер­вый ра­бо­чий, если из­вест­но, что он за час де­ла­ет на 1 де­таль боль­ше?

11. B 14 № 287503.

Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 3

1. B 1 № 504246. Уста­нов­ка двух счётчи­ков воды (хо­лод­ной и го­ря­чей) стоит 2500 руб. До уста­нов­ки счётчи­ков Алек­сандр пла­тил за воду (хо­лод­ную и го­ря­чую) еже­ме­сяч­но 1700 руб. После уста­нов­ки счётчи­ков ока­за­лось, что в сред­нем за месяц он рас­хо­ду­ет воды на 1000 руб. при тех же та­ри­фах на воду. За какое наи­мень­шее ко­ли­че­ство ме­ся­цев при тех же та­ри­фах на воду уста­нов­ка счётчи­ков оку­пит­ся?

2. B 2 № 27529. На ри­сун­ке изоб­ра­жен гра­фик осад­ков в г. Ка­ли­нин­гра­де с 4 по 10 фев­ра­ля 1974 г. На оси абс­цисс от­кла­ды­ва­ют­ся дни, на оси ор­ди­нат — осад­ки в мм. Опре­де­ли­те по ри­сун­ку, сколь­ко дней из дан­но­го пе­ри­о­да вы­па­да­ло от 2 до 8 мм осад­ков.

 

 

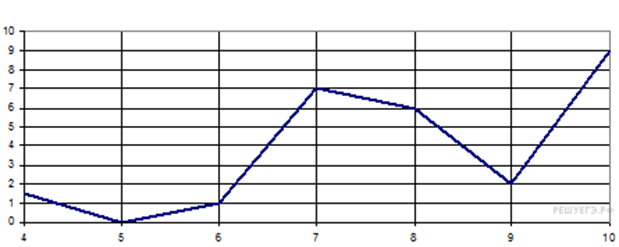
3. B 3 № 26683. 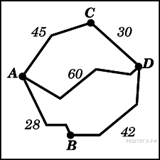Из пунк­та А в пункт D ведут три до­ро­ги. Через пунктВ едет гру­зо­вик со сред­ней ско­ро­стью 35 км/ч, через пункт С едет ав­то­бус со сред­ней ско­ро­стью 30 км/ч. Тре­тья до­ро­га — без про­ме­жу­точ­ных пунк­тов, и по ней дви­жет­ся лег­ко­вой ав­то­мо­биль со сред­ней ско­ро­стью 40 км/ч. На ри­сун­ке по­ка­за­на схема дорог и рас­сто­я­ние между пунк­та­ми по до­ро­гам, вы­ра­жен­ное в ки­ло­мет­рах.

Все три ав­то­мо­би­ля од­но­вре­мен­но вы­еха­ли из А. Какой ав­то­мо­биль до­брал­ся до D позже дру­гих? В от­ве­те ука­жи­те, сколь­ко часов он на­хо­дил­ся в до­ро­ге.

4. B 4 № 27649. 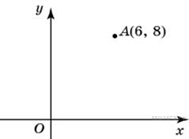Най­ди­те рас­сто­я­ние от точки A с ко­ор­ди­на­та­ми (6; 8) до оси абс­цисс.

5. B 5 № 1016. Мак­сим с папой решил по­ка­тать­ся на ко­ле­се обо­зре­ния. Всего на ко­ле­се 30 ка­би­нок, из них 11 – синие, 7 – зе­ле­ные, осталь­ные – оран­же­вые. Ка­бин­ки по оче­ре­ди под­хо­дят к плат­фор­ме для по­сад­ки. Най­ди­те ве­ро­ят­ность того, что Мак­сим про­ка­тит­ся в оран­же­вой ка­бин­ке.

6. B 6 № 3185. Най­ди­те ко­рень урав­не­ния .

7. B 7 № 27871. 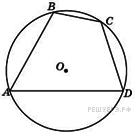Угол  че­ты­рех­уголь­ни­ка , впи­сан­но­го в окруж­ность, равен . Най­ди­те угол  этого че­ты­рех­уголь­ни­ка. Ответ дайте в гра­ду­сах.

8. B 10 № 26749. Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 41987.

По за­ко­ну Ома для пол­ной цепи сила тока, из­ме­ря­е­мая в ам­пе­рах, равна , где  — ЭДС ис­точ­ни­ка (в воль­тах),  Ом — его внут­рен­нее со­про­тив­ле­ние,  — со­про­тив­ле­ние цепи (в омах). При каком наи­мень­шем со­про­тив­ле­нии цепи сила тока будет со­став­лять не более  от силы тока ко­рот­ко­го за­мы­ка­ния ? (Ответ вы­ра­зи­те в омах.)

10. B 13 № 26597. Пер­вая труба про­пус­ка­ет на 1 литр воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет пер­вая труба, если ре­зер­ву­ар объ­е­мом 110 лит­ров она за­пол­ня­ет на 1 ми­ну­ту доль­ше, чем вто­рая труба?

11. B 14 № 287103. Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 4

1. B 1 № 77342. Пачка сли­воч­но­го масла стоит 60 руб­лей. Пен­си­о­не­рам ма­га­зин де­ла­ет скид­ку 5%. Сколь­ко руб­лей за­пла­тит пен­си­о­нер за пачку масла?

 

2. B 2 № 27510.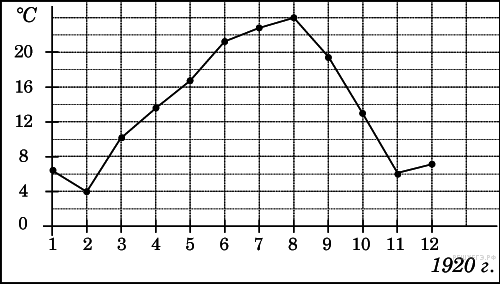

На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра воз­ду­ха в Сочи за каж­дый месяц 1920 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся ме­ся­цы, по вер­ти­ка­ли — тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Для на­гляд­но­сти жир­ные точки со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку наи­мень­шую сред­не­ме­сяч­ную тем­пе­ра­ту­ру в пе­ри­од с мая по де­кабрь 1920 года. Ответ дайте в гра­ду­сах Цель­сия.

 

3. B 3 № 505395. В трёх са­ло­нах со­то­вой связи один и тот же те­ле­фон продаётся в кре­дит на раз­ных усло­ви­ях. Усло­вия даны в таб­ли­це.

 

Салон	Цена те­ле­фо­на (руб.)	Пер­во­на­чаль­ный взнос (в % от цены)	Срок кре­ди­та (мес.)	Сумма еже­ме­сяч­но­го пла­те­жа (руб.)
Эп­си­лон	15 400	25	12	1390
Дель­та	16 200	5	6	3240
Омик­рон	16 000	25	12	1350

 

Опре­де­ли­те, в каком из са­ло­нов по­куп­ка обойдётся де­шев­ле всего (с учётом пе­ре­пла­ты). В от­ве­те за­пи­ши­те эту сумму в руб­лях.

4. B 4 № 27596. Най­ди­те пло­щадь круга, длина окруж­но­сти ко­то­ро­го равна .

5. B 5 № 283477. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют три­жды. Най­ди­те ве­ро­ят­ность того, что орел вы­па­дет все три раза.

6. B 6 № 3185. Най­ди­те ко­рень урав­не­ния .

7. B 7 № 27899. 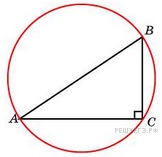В тре­уголь­ни­ке  , угол  равен 90°. Ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка равен 5. Най­ди­те .

8. B 10 № 69485.

Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 41493. За­ви­си­мость тем­пе­ра­ту­ры (в гра­ду­сах Кель­ви­на) от вре­ме­ни для на­гре­ва­тель­но­го эле­мен­та не­ко­то­ро­го при­бо­ра была по­лу­че­на экс­пе­ри­мен­таль­но и на ис­сле­ду­е­мом ин­тер­ва­ле тем­пе­ра­тур опре­де­ля­ет­ся вы­ра­же­ни­ем , где t — время в ми­ну­тах,  К,  К/мин,  К/мин. Из­вест­но, что при тем­пе­ра­ту­ре на­гре­ва­те­ля свыше 1600 К при­бор может ис­пор­тить­ся, по­это­му его нужно от­клю­чать. Опре­де­ли­те, через какое наи­боль­шее время после на­ча­ла ра­бо­ты нужно от­клю­чать при­бор. Ответ вы­ра­зи­те в ми­ну­тах.

10. B 13 № 99605. Первую треть трас­сы ав­то­мо­биль ехал со ско­ро­стью 60 км/ч, вто­рую треть – со ско­ро­стью 120 км/ч, а по­след­нюю – со ско­ро­стью 110 км/ч. Най­ди­те сред­нюю ско­рость ав­то­мо­би­ля на про­тя­же­нии всего пути. Ответ дайте в км/ч.

11. B 14 № 505151. Най­ди­те точку мак­си­му­ма функ­ции 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 5

1. B 1 № 26621. Ма­га­зин за­ку­па­ет цве­точ­ные горш­ки по опто­вой цене 120 руб­лей за штуку и про­да­ет с на­цен­кой 20%. Какое наи­боль­шее число таких горш­ков можно ку­пить в этом ма­га­зи­не на 1000 руб­лей?

 

2. B 2 № 27518. На диа­грам­ме по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра воз­ду­ха в Ека­те­рин­бур­ге (Сверд­лов­ске) за каж­дый месяц 1973 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся ме­ся­цы, по вер­ти­ка­ли — тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Опре­де­ли­те по диа­грам­ме наи­боль­шую сред­не­ме­сяч­ную тем­пе­ра­ту­ру во вто­рой по­ло­ви­не 1973 года. Ответ дайте в гра­ду­сах Цель­сия.

 

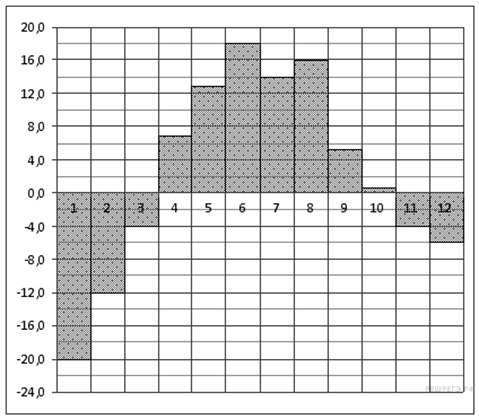
3. B 3 № 41085.

Стро­и­тель­ная фирма пла­ни­ру­ет ку­пить 70 м³ пе­нобло­ков у од­но­го из трех по­став­щи­ков. Цены и усло­вия до­став­ки при­ве­де­ны в таб­ли­це. Сколь­ко руб­лей будет сто­ить самая де­ше­вая по­куп­ка с до­став­кой?

 

 

 

4. B 4 № 248697. Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см × 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

 

 

 

 

 

 

 

 

5. B 5 № 320189. В не­ко­то­ром го­ро­де из 5000 по­явив­ших­ся на свет мла­ден­цев 2512 маль­чи­ков. Най­ди­те ча­сто­ту рож­де­ния де­во­чек в этом го­ро­де. Ре­зуль­тат округ­ли­те до ты­сяч­ных.

6. B 6 № 26665. Най­ди­те ко­рень урав­не­ния: . Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.

7. B 7 № 27363. 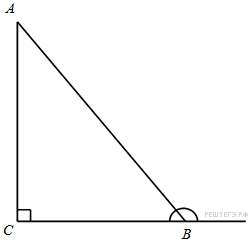В тре­уголь­ни­ке  угол  равен 90°, . Най­ди­те ко­си­нус внеш­не­го угла при вер­ши­не .

8. B 10 № 77418. Вы­чис­ли­те зна­че­ние вы­ра­же­ния: .

9. B 11 № 27970. Для по­лу­че­ния на экра­не уве­ли­чен­но­го изоб­ра­же­ния лам­поч­ки в ла­бо­ра­то­рии ис­поль­зу­ет­ся со­би­ра­ю­щая линза с глав­ным фо­кус­ным рас­сто­я­ни­ем  см. Рас­сто­я­ние  от линзы до лам­поч­ки может из­ме­нять­ся в пре­де­лах от 30 до 50 см, а рас­сто­я­ние  от линзы до экра­на – в пре­де­лах от 150 до 180 см. Изоб­ра­же­ние на экра­не будет чет­ким, если вы­пол­не­но со­от­но­ше­ние. Ука­жи­те, на каком наи­мень­шем рас­сто­я­нии от линзы можно по­ме­стить лам­поч­ку, чтобы еe изоб­ра­же­ние на экра­не было чeтким. Ответ вы­ра­зи­те в сан­ти­мет­рах.

10. B 13 № 506102. Вес­ной катер идёт про­тив те­че­ния реки в  раза мед­лен­нее, чем по те­че­нию. Летом те­че­ние ста­но­вит­ся на 1 км/ч мед­лен­нее. По­это­му летом катер идёт про­тив те­че­ния в  раза мед­лен­нее, чем по те­че­нию. Най­ди­те ско­рость те­че­ния вес­ной (в км/ч).

11. B 14 № 287303.

Най­ди­те наи­боль­шее зна­че­ние функ­ции .

Вариант № 6

1. B 1 № 26643. Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. За­ра­бот­ная плата Ивана Кузь­ми­ча равна 12 500 руб­лей. Сколь­ко руб­лей он по­лу­чит после вы­че­та на­ло­га на до­хо­ды?

 

2. B 2 № 263977.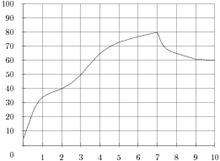

На гра­фи­ке по­ка­зан про­цесс разо­гре­ва дви­га­те­ля лег­ко­во­го ав­то­мо­би­ля. На оси абс­цисс от­кла­ды­ва­ет­ся время в ми­ну­тах, про­шед­шее от за­пус­ка дви­га­те­ля, на оси ор­ди­нат — тем­пе­ра­ту­ра дви­га­те­ля в гра­ду­сах Цель­сия. Опре­де­ли­те по гра­фи­ку, до сколь­ки гра­ду­сов Цель­сия дви­га­тель на­грел­ся за пер­вые 7 минут.

3. B 3 № 26679. Стро­и­тель­ной фирме нужно при­об­ре­сти 40 ку­бо­мет­ров стро­и­тель­но­го бруса у од­но­го из трех по­став­щи­ков. Ка­ко­ва наи­мень­шая сто­и­мость такой по­куп­ки с до­став­кой (в руб­лях)? Цены и усло­вия до­став­ки при­ве­де­ны в таб­ли­це.

 

4. B 4 № 5255.

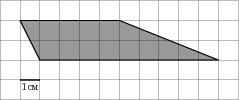На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см  1 см изоб­ра­же­на тра­пе­ция (см. ри­су­нок). Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

5. B 5 № 286119.

Кон­курс ис­пол­ни­те­лей про­во­дит­ся в 5 дней. Всего за­яв­ле­но 80 вы­ступ­ле­ний — по од­но­му от каж­дой стра­ны. В пер­вый день 16 вы­ступ­ле­ний, осталь­ные рас­пре­де­ле­ны по­ров­ну между остав­ши­ми­ся днями. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что вы­ступ­ле­ние пред­ста­ви­те­ля Рос­сии со­сто­ит­ся в тре­тий день кон­кур­са?

6. B 6 № 13687.

Най­ди­те ко­рень урав­не­ния: 

7. B 7 № 27445. 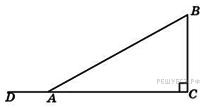В тре­уголь­ни­ке  угол  равен 90°, угол равен . Най­ди­те синус угла .

8. B 10 № 26827. Най­ди­те зна­че­ние вы­ра­же­ния  при .

9. B 11 № 41313.

За­ви­си­мость объeма спро­са  (еди­ниц в месяц) на про­дук­цию пред­при­я­тия-мо­но­по­ли­ста от цены  (тыс. руб.) задаeтся фор­му­лой . Вы­руч­ка пред­при­я­тия за месяц  (в тыс. руб.) вы­чис­ля­ет­ся по фор­му­ле . Опре­де­ли­те наи­боль­шую цену , при ко­то­рой ме­сяч­ная вы­руч­ка  со­ста­вит не менее 350 тыс. руб. Ответ при­ве­ди­те в тыс. руб.

10. B 13 № 39507. От при­ста­ни А к при­ста­ни В от­пра­вил­ся с по­сто­ян­ной ско­ро­стью пер­вый теп­ло­ход, а через 8 часов после этого сле­дом за ним со ско­ро­стью, на 8 км/ч боль­шей, от­пра­вил­ся вто­рой. Рас­сто­я­ние между при­ста­ня­ми равно 209 км. Най­ди­те ско­рость пер­во­го теп­ло­хо­да, если в пункт В оба теп­ло­хо­да при­бы­ли од­но­вре­мен­но. Ответ дайте в км/ч.

11. B 14 № 286903. Най­ди­те наи­боль­шее зна­че­ние функ­ции .

 

 

           

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 7

1. B 1 № 26632. Так­сист за месяц про­ехал 6000 км. Сто­и­мость 1 литра бен­зи­на — 20 руб­лей. Сред­ний рас­ход бен­зи­на на 100 км со­став­ля­ет 9 лит­ров. Сколь­ко руб­лей по­тра­тил так­сист на бен­зин за этот месяц?

 

2. B 2 № 28763. На диа­грам­ме по­ка­за­но ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти во все дни с 10 по 29 но­яб­ря 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся дни ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство по­се­ти­те­лей сайта за дан­ный день. Опре­де­ли­те по диа­грам­ме, сколь­ко раз ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти при­ни­ма­ло наи­боль­шее зна­че­ние.

 

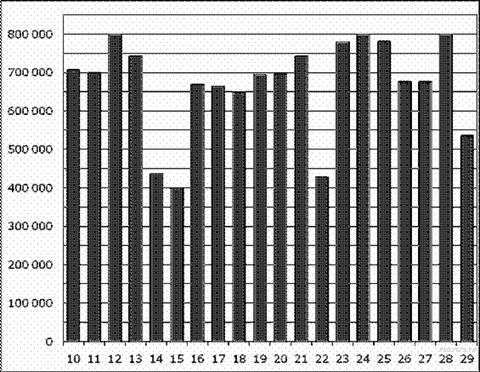
3. B 3 № 505374. В трёх са­ло­нах со­то­вой связи один и тот же те­ле­фон продаётся в кре­дит на раз­ных усло­ви­ях. Усло­вия даны в таб­ли­це.

 

Салон	Цена те­ле­фо­на (руб.)	Пер­во­на­чаль­ный взнос (в % от цены)	Срок кре­ди­та (мес.)	Сумма еже­ме­сяч­но­го пла­те­жа (руб.)
Эп­си­лон	11 100	20	12	870
Дель­та	12 500	15	6	1820
Омик­рон	12 700	25	6	1620

 

Опре­де­ли­те, в каком из са­ло­нов по­куп­ка обойдётся де­шев­ле всего (с учётом пе­ре­пла­ты). В от­ве­те за­пи­ши­те эту сумму в руб­лях.

4. B 4 № 244991. 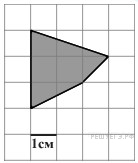Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

 

5. B 5 № 286381.

В сбор­ни­ке би­ле­тов по ис­то­рии всего 20 би­ле­тов, в 12 из них встре­ча­ет­ся во­прос о смут­ном вре­ме­ни. Най­ди­те ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку не до­ста­нет­ся во­про­са о смут­ном вре­ме­ни.

6. B 6 № 77368. Ре­ши­те урав­не­ние .

7. B 7 № 27843. 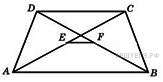Ос­но­ва­ния тра­пе­ции равны 3 и 2. Най­ди­те от­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны диа­го­на­лей тра­пе­ции.

8. B 10 № 26811. Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 27953. При тем­пе­ра­ту­ре  рельс имеет длину  м. При воз­рас­та­нии тем­пе­ра­ту­ры про­ис­хо­дит теп­ло­вое рас­ши­ре­ние рель­са, и его длина, вы­ра­жен­ная в мет­рах, ме­ня­ет­ся по за­ко­ну, где  — ко­эф­фи­ци­ент теп­ло­во­го рас­ши­ре­ния,  — тем­пе­ра­ту­ра (в гра­ду­сах Цель­сия). При какой тем­пе­ра­ту­ре рельс удли­нит­ся на 3 мм? Ответ вы­ра­зи­те в гра­ду­сах Цель­сия.

10. B 13 № 107387. В 2008 году в го­род­ском квар­та­ле про­жи­ва­ло 40 000 че­ло­век. В 2009 году, в ре­зуль­та­те стро­и­тель­ства новых домов, число жи­те­лей вы­рос­ло на 3%, а в 2010 году  — на 9% по срав­не­нию с 2009 годом. Сколь­ко че­ло­век стало про­жи­вать в квар­та­ле в 2010 году?

11. B 14 № 287203.

Най­ди­те наи­мень­шее зна­че­ние функ­ции .

 

           

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 8

1. B 1 № 282957. На ав­то­за­прав­ке кли­ент отдал кас­си­ру 1000 руб­лей и залил в бак 22 литра бен­зи­на по цене 33 руб. 20 коп.за литр. Сколь­ко руб­лей сдачи он дол­жен по­лу­чить у кас­си­ра?

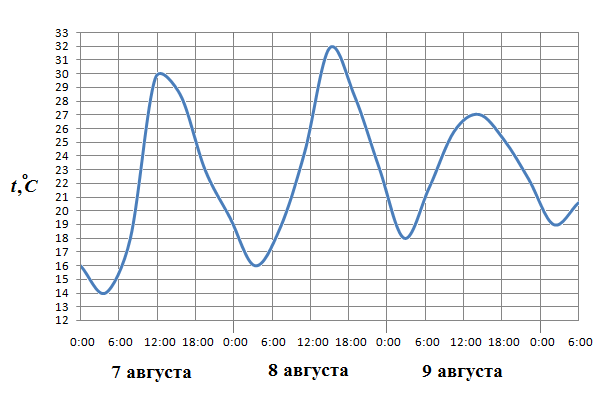
2. B 2 № 5373.

На ри­сун­ке по­ка­за­но из­ме­не­ние тем­пе­ра­ту­ры воз­ду­ха на про­тя­же­нии трех суток. По го­ри­зон­та­ли ука­зы­ва­ет­ся дата и время суток, по вер­ти­ка­ли — зна­че­ние тем­пе­ра­ту­ры в гра­ду­сах Цель­сия. Опре­де­ли­те по ри­сун­ку наи­мень­шую тем­пе­ра­ту­ру воз­ду­ха 7 ав­гу­ста. Ответ дайте в гра­ду­сах Цель­сия.

 

3. B 3 № 26685. В таб­ли­це даны та­ри­фы на услу­ги трех фирм такси. Пред­по­ла­га­ет­ся по­езд­ка дли­тель­но­стью 70 минут. Нужно вы­брать фирму, в ко­то­рой заказ будет сто­ить де­шев­ле всего. Сколь­ко руб­лей будет сто­ить этот заказ?

 

 

*Если по­езд­ка про­дол­жа­ет­ся мень­ше ука­зан­но­го вре­ме­ни, она опла­чи­ва­ет­ся по сто­и­мо­сти ми­ни­маль­ной по­езд­ки.

4. B 4 № 27603. Най­ди­те пе­ри­метр пря­мо­уголь­ни­ка, если его пло­щадь равна 18, а от­но­ше­ние со­сед­них сто­рон равно 1:2.

5. B 5 № 321399. На олим­пиа­де по рус­ско­му языку участ­ни­ков рас­са­жи­ва­ют по трём ауди­то­ри­ям. В пер­вых двух по 120 че­ло­век, остав­ших­ся про­во­дят в за­пас­ную ауди­то­рию в дру­гом кор­пу­се. При подсчёте вы­яс­ни­лось, что всего было 400 участ­ни­ков. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ный участ­ник писал олим­пи­а­ду в за­пас­ной ауди­то­рии.

 

6. B 6 № 100787. Ре­ши­те урав­не­ние . (По­вто­ря­ет­ся с №77369)

7. B 7 № 51343. Дуга окруж­но­сти AC, не со­дер­жа­щая точки B, со­став­ля­ет . А дуга окруж­но­сти BC, не со­дер­жа­щая точки A, со­став­ля­ет . Най­ди­те впи­сан­ный угол ACB. Ответ дайте в гра­ду­сах.

8. B 10 № 26883. Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 41471.

Кам­не­ме­та­тель­ная ма­ши­на вы­стре­ли­ва­ет камни под не­ко­то­рым ост­рым углом к го­ри­зон­ту. Тра­ек­то­рия полeта камня опи­сы­ва­ет­ся фор­му­лой , где  м,  — по­сто­ян­ные па­ра­мет­ры,  (м) — сме­ще­ние камня по го­ри­зон­та­ли,  (м) — вы­со­та камня над землeй. На каком наи­боль­шем рас­сто­я­нии (в мет­рах) от кре­пост­ной стены вы­со­той 19 м нужно рас­по­ло­жить ма­ши­ну, чтобы камни про­ле­та­ли над сте­ной на вы­со­те не менее 1 метра?

10. B 13 № 99597. Пер­вый ве­ло­си­пе­дист вы­ехал из по­сел­ка по шоссе со ско­ро­стью 15 км/ч. Через час после него со ско­ро­стью 10 км/ч из того же по­сел­ка в том же на­прав­ле­нии вы­ехал вто­рой ве­ло­си­пе­дист, а еще через час после этого – тре­тий. Най­ди­те ско­рость тре­тье­го ве­ло­си­пе­ди­ста, если сна­ча­ла он до­гнал вто­ро­го, а через 2 часа 20 минут после этого до­гнал пер­во­го. Ответ дайте в км/ч.

11. B 14 № 287703.

Най­ди­те наи­боль­шее зна­че­ние функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 9

1. B 1 № 26633. Кли­ент взял в банке кре­дит 12 000 руб­лей на год под 16%. Он дол­жен по­га­шать кре­дит, внося в банк еже­ме­сяч­но оди­на­ко­вую сумму денег, с тем чтобы через год вы­пла­тить всю сумму, взя­тую в кре­дит, вме­сте с про­цен­та­ми. Сколь­ко руб­лей он дол­жен вно­сить в банк еже­ме­сяч­но?

 

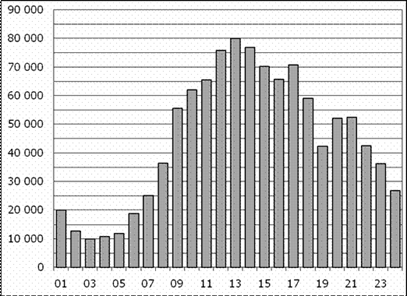
2. B 2 № 77255.

На диа­грам­ме по­ка­за­но ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти в те­че­ние каж­до­го часа 8 де­каб­ря 2009 года. По го­ри­зон­та­ли ука­зы­ва­ет­ся номер часа, по вер­ти­ка­ли — ко­ли­че­ство по­се­ти­те­лей сайта за дан­ный час. Опре­де­ли­те по диа­грам­ме, каким было наи­боль­шее ко­ли­че­ство по­се­ти­те­лей в час с 1:00 до 7:00 в дан­ный день на сайте РИАН.

3. B 3 № 77363. Вася за­гру­жа­ет на свой ком­пью­тер из Ин­тер­не­та файл раз­ме­ром 30 Мб за 28 се­кунд. Петя за­гру­жа­ет файл раз­ме­ром 28 Мб за 24 се­кун­ды, а Миша за­гру­жа­ет файл раз­ме­ром 38 Мб за 32 се­кун­ды. Сколь­ко се­кунд будет за­гру­жать­ся файл раз­ме­ром 665 Мб на ком­пью­тер с наи­боль­шей ско­ро­стью за­груз­ки?

4. B 4 № 27453. 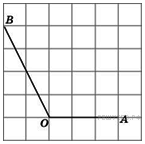Най­ди­те тан­генс угла .

5. B 5 № 285927. В сбор­ни­ке би­ле­тов по ма­те­ма­ти­ке всего 25 би­ле­тов, в 10 из них встре­ча­ет­ся во­прос по не­ра­вен­ствам. Най­ди­те ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку не до­ста­нет­ся во­про­са по не­ра­вен­ствам.

6. B 6 № 103019.

 

Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

7. B 7 № 282851. В ромбе ABCD угол ABC равен 122°. Най­ди­те угол ACD. Ответ дайте в гра­ду­сах.

8. B 10 № 66653.

Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 41955.

Перед от­прав­кой теп­ло­воз издал гудок с ча­сто­той  Гц. Чуть позже издал гудок подъ­ез­жа­ю­щий к плат­фор­ме теп­ло­воз. Из-за эф­фек­та До­пле­ра ча­сто­та вто­ро­го гудка  боль­ше пер­во­го: она за­ви­сит от ско­ро­сти теп­ло­во­за по за­ко­ну  (Гц), где  — ско­рость звука в звука (в м/с). Че­ло­век, сто­я­щий на плат­фор­ме, раз­ли­ча­ет сиг­на­лы по тону, если они от­ли­ча­ют­ся не менее, чем на 7 Гц. Опре­де­ли­те, с какой ми­ни­маль­ной ско­ро­стью при­бли­жал­ся к плат­фор­ме теп­ло­воз, если че­ло­век смог раз­ли­чить сиг­на­лы, а  м/с. Ответ вы­ра­зи­те в м/с.

10. B 13 № 39633. Заказ на 272 де­та­ли пер­вый ра­бо­чий вы­пол­ня­ет на 1 час быст­рее, чем вто­рой. Сколь­ко де­та­лей в час де­ла­ет вто­рой ра­бо­чий, если из­вест­но, что пер­вый за час де­ла­ет на 1 де­таль боль­ше?

11. B 14 № 287103. Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 10

1. B 1 № 26618. Фла­кон шам­пу­ня стоит 160 руб­лей. Какое наи­боль­шее число фла­ко­нов можно ку­пить на 1000 руб­лей во время рас­про­да­жи, когда скид­ка со­став­ля­ет 25% ?

2. B 2 № 263799.

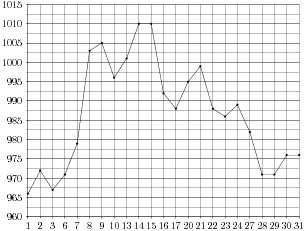
На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена зо­ло­та, уста­нов­лен­ная Цен­тро­бан­ком РФ во все ра­бо­чие дни в ок­тяб­ре 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена зо­ло­та в руб­лях за грамм. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, сколь­ко дней из дан­но­го пе­ри­о­да цена зо­ло­та была между 970 и 980 руб­ля­ми за грамм.

3. B 3 № 26683. 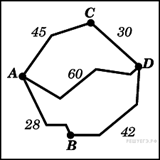Из пунк­та А в пункт D ведут три до­ро­ги. Через пунктВ едет гру­зо­вик со сред­ней ско­ро­стью 35 км/ч, через пункт С едет ав­то­бус со сред­ней ско­ро­стью 30 км/ч. Тре­тья до­ро­га — без про­ме­жу­точ­ных пунк­тов, и по ней дви­жет­ся лег­ко­вой ав­то­мо­биль со сред­ней ско­ро­стью 40 км/ч. На ри­сун­ке по­ка­за­на схема дорог и рас­сто­я­ние между пунк­та­ми по до­ро­гам, вы­ра­жен­ное в ки­ло­мет­рах.

Все три ав­то­мо­би­ля од­но­вре­мен­но вы­еха­ли из А. Какой ав­то­мо­биль до­брал­ся до D позже дру­гих? В от­ве­те ука­жи­те, сколь­ко часов он на­хо­дил­ся в до­ро­ге.

4. B 4 № 322727. На клет­ча­той бу­ма­ге на­ри­со­ва­но два круга. Пло­щадь внут­рен­не­го круга равна 2. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

 

 

5. B 5 № 504533. Из мно­же­ства на­ту­раль­ных чисел от 25 до 39 на­уда­чу вы­би­ра­ют одно число. Ка­ко­ва ве­ро­ят­ность того, что оно де­лит­ся на 5?

6. B 6 № 505398. Най­ди­те ко­рень урав­не­ния 

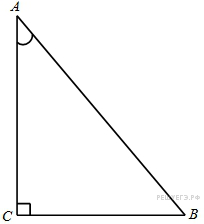
7. B 7 № 27237. В тре­уголь­ни­ке  угол  равен 90°, , . Най­ди­те .

8. B 10 № 92055.

Най­ди­те зна­че­ние вы­ра­же­ния  при .

9. B 11 № 42739.

Ав­то­мо­биль, масса ко­то­ро­го равна  кг, на­чи­на­ет дви­гать­ся с уско­ре­ни­ем, ко­то­рое в те­че­ние  се­кунд остаeтся не­из­мен­ным, и про­хо­дит за это время путь  мет­ров. Зна­че­ние силы (в нью­то­нах), при­ло­жен­ной в это время к ав­то­мо­би­лю, равно . Опре­де­ли­те наи­боль­шее время после на­ча­ла дви­же­ния ав­то­мо­би­ля, за ко­то­рое он пройдeт ука­зан­ный путь, если из­вест­но, что сила , при­ло­жен­ная к ав­то­мо­би­лю, не мень­ше 1440 Н. Ответ вы­ра­зи­те в се­кун­дах.

10. B 13 № 505447. Име­ет­ся два рас­тво­ра. Пер­вый со­дер­жит 10% соли, вто­рой — 30% соли. Из этих двух рас­тво­ров по­лу­чи­ли тре­тий рас­твор мас­сой 200 кг, со­дер­жа­щий 25% соли. На сколь­ко ки­ло­грам­мов масса пер­во­го рас­тво­ра мень­ше массы вто­ро­го?

11. B 14 № 245175. Най­ди­те наи­мень­шее зна­че­ние функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 11

1. B 1 № 77343. Тет­радь стоит 24 рубля. Сколь­ко руб­лей за­пла­тит по­ку­па­тель за 60 тет­ра­дей, если при по­куп­ке боль­ше 50 тет­ра­дей ма­га­зин де­ла­ет скид­ку 10% от сто­и­мо­сти всей по­куп­ки?

 

2. B 2 № 263597.

 

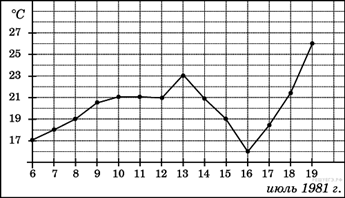На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на сред­не­су­точ­ная тем­пе­ра­ту­ра воз­ду­ха в Бре­сте каж­дый день с 6 по 19 июля 1981 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Для на­гляд­но­сти жир­ные точки со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, какая была тем­пе­ра­ту­ра 15 июля. Ответ дайте в гра­ду­сах Цель­сия.

 

 

 

3. B 3 № 18759.

Для того, чтобы свя­зать сви­тер, хо­зяй­ке нужно 600 грам­мов шер­сти крас­но­го цвета. Можно ку­пить крас­ную пряжу по цене 80 руб­лей за 100 г, а можно ку­пить не­окра­шен­ную пряжу по цене 50 руб­лей за 100 г и окра­сить ее. Один па­ке­тик крас­ки стоит 20 руб­лей и рас­счи­тан на окрас­ку 300 г пряжи. Какой ва­ри­ант по­куп­ки де­шев­ле? В ответ на­пи­ши­те, сколь­ко руб­лей будет сто­ить эта по­куп­ка.

4. B 4 № 505459. 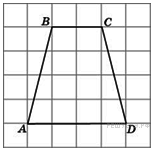На клет­ча­той бу­ма­ге изоб­ра­же­на тра­пе­ция. Найти длину сред­ней линии этой тра­пе­ции (в сан­ти­мет­рах).

5. B 5 № 1012. В фирме такси в дан­ный мо­мент сво­бод­но 16 машин: 4 чер­ных, 3 синих и 9 белых. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­це. Най­ди­те ве­ро­ят­ность того, что к ней при­е­дет чер­ное такси.

6. B 6 № 104691.

 

Ре­ши­те урав­не­ние .

7. B 7 № 27400. 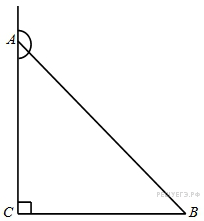В тре­уголь­ни­ке  угол  равен 90°, тан­генс внеш­не­го угла при вер­ши­не  равен -0,1. Най­ди­те .

8. B 10 № 96369.

Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 41691.

Де­та­лью не­ко­то­ро­го при­бо­ра яв­ля­ет­ся вра­ща­ю­ща­я­ся ка­туш­ка. Она со­сто­ит из трeх од­но­род­ных со­ос­ных ци­лин­дров: цен­траль­но­го мас­сой  кг и ра­ди­у­са  см, и двух бо­ко­вых с мас­са­ми  кг и с ра­ди­у­са­ми . При этом мо­мент инер­ции ка­туш­ки от­но­си­тель­но оси вра­ще­ния, вы­ра­жа­е­мый в , даeтся фор­му­лой . При каком мак­си­маль­ном зна­че­нии  мо­мент инер­ции ка­туш­ки не пре­вы­ша­ет пре­дель­но­го зна­че­ния ? Ответ вы­ра­зи­те в сан­ти­мет­рах.

10. B 13 № 99591. Рас­сто­я­ние между го­ро­да­ми  и  равно 470 км. Из го­ро­да  в город  вы­ехал пер­вый ав­то­мо­биль, а через 3 часа после этого нав­стре­чу ему из го­ро­да  вы­ехал со ско­ро­стью 60 км/ч вто­рой ав­то­мо­биль. Най­ди­те ско­рость пер­во­го ав­то­мо­би­ля, если ав­то­мо­би­ли встре­ти­лись на рас­сто­я­нии 350 км от го­ро­да . Ответ дайте в км/ч.

11. B 14 № 245179. Най­ди­те наи­мень­шее зна­че­ние функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 12

    1. Сту­дент по­лу­чил свой пер­вый го­но­рар в раз­ме­ре 800 руб­лей за вы­пол­нен­ный пе­ре­вод. Он решил на все по­лу­чен­ные день­ги ку­пить букет роз для своей учи­тель­ни­цы ан­глий­ско­го языка. Какое наи­боль­шее ко­ли­че­ство роз смо­жет ку­пить сту­дент, если удер­жан­ный у него налог на до­хо­ды со­став­ля­ет 13% го­но­ра­ра, розы стоят 100 руб­лей за штуку и букет дол­жен со­сто­ять из не­чет­но­го числа цве­тов?

2. B 2 № 26876. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­но су­точ­ное ко­ли­че­ство осад­ков, вы­па­дав­ших в Том­ске с 8 по 24 ян­ва­ря 2005 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство осад­ков, вы­пав­ших в со­от­вет­ству­ю­щий день, в мил­ли­мет­рах. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, какое наи­боль­шее ко­ли­че­ство осад­ков вы­па­да­ло в пе­ри­од с 13 по 20 ян­ва­ря. Ответ дайте в мил­ли­мет­рах.

 

 

3. B 3 № 18759.

Для того, чтобы свя­зать сви­тер, хо­зяй­ке нужно 600 грам­мов шер­сти крас­но­го цвета. Можно ку­пить крас­ную пряжу по цене 80 руб­лей за 100 г, а можно ку­пить не­окра­шен­ную пряжу по цене 50 руб­лей за 100 г и окра­сить ее. Один па­ке­тик крас­ки стоит 20 руб­лей и рас­счи­тан на окрас­ку 300 г пряжи. Какой ва­ри­ант по­куп­ки де­шев­ле? В ответ на­пи­ши­те, сколь­ко руб­лей будет сто­ить эта по­куп­ка.

4. B 4 № 27705. Най­ди­те пло­щадь тра­пе­ции, вер­ши­ны ко­то­рой имеют ко­ор­ди­на­ты (2; 2), (8; 4), (8; 8), (2; 10).

5. B 5 № 320851. На кла­ви­а­ту­ре те­ле­фо­на 10 цифр, от 0 до 9. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но на­жа­тая цифра будет боль­ше 2, но мень­ше 7?

 

6. B 6 № 26655. Най­ди­те ко­рень урав­не­ния .

 

 

 

 

 

 

 

 

7. B 7 № 30465.

В тре­уголь­ни­ке ABC угол C равен 90°, , . Най­ди­те вы­со­туCH.

 

8. B 10 № 87483.

Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 27972. По за­ко­ну Ома для пол­ной цепи сила тока, из­ме­ря­е­мая в ам­пе­рах, равна , где  – ЭДС ис­точ­ни­ка (в воль­тах),  Ом – его внут­рен­нее со­про­тив­ле­ние,  – со­про­тив­ле­ние цепи (в Омах). При каком наи­мень­шем со­про­тив­ле­нии цепи сила тока будет со­став­лять не более  от силы тока ко­рот­ко­го за­мы­ка­ния  ? (Ответ вы­ра­зи­те в Омах.)

10. B 13 № 112517. Из го­ро­дов A и B, рас­сто­я­ние между ко­то­ры­ми равно 300 км, нав­стре­чу друг другу од­но­вре­мен­но вы­еха­ли два ав­то­мо­би­ля и встре­ти­лись через 2 часа на рас­сто­я­нии 180 км от го­ро­да B. Най­ди­те ско­рость ав­то­мо­би­ля, вы­ехав­ше­го из го­ро­да A. Ответ дайте в км/ч.

11. B 14 № 245183. Най­ди­те наи­мень­шее зна­че­ние функ­ции 

 

 

 

           

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 13

1. B 1 № 77344. При­зе­ра­ми го­род­ской олим­пи­а­ды по ма­те­ма­ти­ке стало 48 уче­ни­ков, что со­ста­ви­ло 12% от числа участ­ни­ков. Сколь­ко че­ло­век участ­во­ва­ло в олим­пиа­де?

 

2. B 2 № 27516. На диа­грам­ме по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра воз­ду­ха в Санкт-Пе­тер­бур­ге за каж­дый месяц 1999 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся ме­ся­цы, по вер­ти­ка­ли — тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Опре­де­ли­те по диа­грам­ме наи­мень­шую сред­не­ме­сяч­ную тем­пе­ра­ту­ру во вто­рой по­ло­ви­не 1999 года. Ответ дайте в гра­ду­сах Цель­сия.

 

3. B 3 № 5453.

Семья из трех че­ло­век едет из Моск­вы в Че­бок­са­ры. Можно ехать по­ез­дом, а можно — на своей ма­ши­не. Билет на поезд на од­но­го че­ло­ве­ка стоит 930 руб­лей. Ав­то­мо­биль рас­хо­ду­ет 11 лит­ров бен­зи­на на 100 ки­ло­мет­ров пути, рас­сто­я­ние по шоссе равно 700 км, а цена бен­зи­на равна 18,5 руб­лей за литр. Сколь­ко руб­лей при­дет­ся за­пла­тить за наи­бо­лее де­ше­вую по­езд­ку на троих?

4. B 4 № 48913. В тре­уголь­ни­ке ABC , вы­со­та AH равна 42. Най­ди­те угол C. Ответ дайте в гра­ду­сах.

5. B 5 № 315953.

 

В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют че­ты­ре­жды. Най­ди­те ве­ро­ят­ность того, что решка вы­па­дет ровно два раза.

 

6. B 6 № 27466. Най­ди­те ко­рень урав­не­ния .

7. B 7 № 245385. Най­ди­те цен­траль­ный угол , если он на  боль­ше впи­сан­но­го угла , опи­ра­ю­ще­го­ся на ту же дугу. Ответ дайте в гра­ду­сах.

 

8. B 10 № 77393. Най­ди­те зна­че­ние вы­ра­же­ния  при .

9. B 11 № 43097.

Во­до­лаз­ный ко­ло­кол, со­дер­жа­щий в на­чаль­ный мо­мент вре­ме­ни  моля воз­ду­ха объeмом  л, мед­лен­но опус­ка­ют на дно водоeма. При этом про­ис­хо­дит изо­тер­ми­че­ское сжа­тие воз­ду­ха до ко­неч­но­го объeма . Ра­бо­та, со­вер­ша­е­мая водой при сжа­тии воз­ду­ха, опре­де­ля­ет­ся вы­ра­же­ни­ем  (Дж), где  по­сто­ян­ная, а  К — тем­пе­ра­ту­ра воз­ду­ха. Какой объeм  (в лит­рах) ста­нет за­ни­мать воз­дух, если при сжа­тии газа была со­вер­ше­на ра­бо­та в 27 840 Дж?

10. B 13 № 26600. Пер­вая труба про­пус­ка­ет на 5 лит­ров воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет вто­рая труба, если ре­зер­ву­ар объ­е­мом 375 лит­ров она за­пол­ня­ет на 10 минут быст­рее, чем пер­вая труба за­пол­ня­ет ре­зер­ву­ар объ­е­мом 500 лит­ров?

11. B 14 № 245181. Най­ди­те точку мак­си­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 14

1. B 1 № 26643. Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. За­ра­бот­ная плата Ивана Кузь­ми­ча равна 12 500 руб­лей. Сколь­ко руб­лей он по­лу­чит после вы­че­та на­ло­га на до­хо­ды?

 

2. B 2 № 263995.

 

На гра­фи­ке по­ка­зан про­цесс разо­гре­ва дви­га­те­ля лег­ко­во­го ав­то­мо­би­ля. На оси абс­цисс от­кла­ды­ва­ет­ся время в ми­ну­тах, про­шед­шее от за­пус­ка дви­га­те­ля, на оси ор­ди­нат — тем­пе­ра­ту­ра дви­га­те­ля в гра­ду­сах Цель­сия.

Опре­де­ли­те по гра­фи­ку, на сколь­ко гра­ду­сов на­гре­ет­ся дви­га­тель со вто­рой по вось­мую ми­ну­ту разо­гре­ва.

 

3. B 3 № 319857. Рей­тин­го­вое агент­ство опре­де­ля­ет рей­тинг со­от­но­ше­ния «цена-ка­че­ство» мик­ро­вол­но­вых печей. Рей­тинг вы­чис­ля­ет­ся на ос­но­ве сред­ней цены  и оце­нок функ­ци­о­наль­но­сти , ка­че­ства  и ди­зай­на . Каж­дый от­дель­ный по­ка­за­тель оце­ни­ва­ет­ся экс­пер­та­ми по 5-балль­ной шкале це­лы­ми чис­ла­ми от 0 до 4. Ито­го­вый рей­тинг вы­чис­ля­ет­ся по фор­му­ле

 

 

В таб­ли­це даны оцен­ки каж­до­го по­ка­за­те­ля для не­сколь­ких мо­де­лей печей. Опре­де­ли­те, какая мо­дель имеет наи­выс­ший рей­тинг. В ответ за­пи­ши­те зна­че­ние этого рей­тин­га.

 

 

 

 

4. B 4 № 245003. 

Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

5. B 5 № 321035.

 

Перед на­ча­лом фут­боль­но­го матча судья бро­са­ет мо­нет­ку, чтобы опре­де­лить, какая из ко­манд начнёт игру с мячом. Ко­ман­да «Сап­фир» иг­ра­ет три матча с раз­ны­ми ко­ман­да­ми. Най­ди­те ве­ро­ят­ность того, что в этих играх «Сап­фир» вы­иг­ра­ет жре­бий ровно два раза.

 

6. B 6 № 13375. Най­ди­те ко­рень урав­не­ния:  В от­ве­те за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

7. B 7 № 27220. В тре­уголь­ни­ке  угол  равен 90°, . Най­ди­те .

8. B 10 № 77393. Най­ди­те зна­че­ние вы­ра­же­ния  при .

9. B 11 № 42831. В ходе рас­па­да ра­дио­ак­тив­но­го изо­то­па, его масса умень­ша­ет­ся по за­ко­ну , где  — на­чаль­ная масса изо­то­па, t (мин) — про­шед­шее от на­чаль­но­го мо­мен­та время, T — пе­ри­од по­лу­рас­па­да в ми­ну­тах. В ла­бо­ра­то­рии по­лу­чи­ли ве­ще­ство, со­дер­жа­щее в на­чаль­ный мо­мент вре­ме­ни  мг изо­то­па Z, пе­ри­од по­лу­рас­па­да ко­то­ро­го  мин. В те­че­ние сколь­ких минут масса изо­то­па будет не мень­ше 17 мг?

10. B 13 № 6005. Катер в 11:00 вышел из пунк­та А в пункт В, рас­по­ло­жен­ный в 30 км от А. Про­быв в пунк­те В 2 часа 40 минут, катер от­пра­вил­ся назад и вер­нул­ся в пункт А в 19:00. Опре­де­ли­те (в км/час) ско­рость те­че­ния реки, если из­вест­но, что соб­ствен­ная ско­рость ка­те­ра равна 12 км/ч.

 

 

11. B 14 № 287703.

Най­ди­те наи­боль­шее зна­че­ние функ­ции .

 

 

Вариант № 15

1. B 1 № 323516. На бен­зо­ко­лон­ке один литр бен­зи­на стоит 32 руб. 60 коп. Во­ди­тель залил в бак 30 лит­ров бен­зи­на и купил бу­тыл­ку воды за 48 руб­лей. Сколь­ко руб­лей сдачи он по­лу­чит с 1500 руб­лей?

2. B 2 № 263865. В ходе хи­ми­че­ской ре­ак­ции ко­ли­че­ство ис­ход­но­го ве­ще­ства (ре­а­ген­та), ко­то­рое еще не всту­пи­ло в ре­ак­цию, со вре­ме­нем по­сте­пен­но умень­ша­ет­ся. На ри­сун­ке эта за­ви­си­мость пред­став­ле­на гра­фи­ком. На оси абс­цисс от­кла­ды­ва­ет­ся время в ми­ну­тах, про­шед­шее с мо­мен­та на­ча­ла ре­ак­ции, на оси ор­ди­нат – масса остав­ше­го­ся ре­а­ген­та, ко­то­рый еще не всту­пил в ре­ак­цию (в грам­мах). Опре­де­ли­те по гра­фи­ку, сколь­ко грам­мов ре­а­ген­та всту­пи­ло в ре­ак­цию за три ми­ну­ты?

 

 

 

3. B 3 № 41085.

Стро­и­тель­ная фирма пла­ни­ру­ет ку­пить 70 м³ пе­нобло­ков у од­но­го из трех по­став­щи­ков. Цены и усло­вия до­став­ки при­ве­де­ны в таб­ли­це. Сколь­ко руб­лей будет сто­ить самая де­ше­вая по­куп­ка с до­став­кой?

 

4. B 4 № 27811. Най­ди­те диа­го­наль пря­мо­уголь­ни­ка, две сто­ро­ны ко­то­ро­го равны  и .

5. B 5 № 1015. В фирме такси в дан­ный мо­мент сво­бод­но 20 машин: 3 белых, 11 синих и 6 серых. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­це. Най­ди­те ве­ро­ят­ность того, что к ней при­е­дет белое такси.

6. B 6 № 13687.

Най­ди­те ко­рень урав­не­ния: 

7. B 7 № 27917. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в пра­виль­ный ше­сти­уголь­ник со сто­ро­ной .

8. B 10 № 92555.

Най­ди­те зна­че­ние вы­ра­же­ния , если .

9. B 11 № 42519. При дви­же­нии ра­ке­ты еe ви­ди­мая для не­по­движ­но­го на­блю­да­те­ля длина, из­ме­ря­е­мая в мет­рах, со­кра­ща­ет­ся по за­ко­ну , где  м — длина по­ко­я­щей­ся ра­ке­ты,  км/с — ско­рость света, а  — ско­рость ра­ке­ты (в км/с). Ка­ко­ва долж­на быть ми­ни­маль­ная ско­рость ра­ке­ты, чтобы еe на­блю­да­е­мая длина стала не более 68 м? Ответ вы­ра­зи­те в км/с.

10. B 13 № 26581. Ве­ло­си­пе­дист вы­ехал с по­сто­ян­ной ско­ро­стью из го­ро­да A в город B, рас­сто­я­ние между ко­то­ры­ми равно 70 км. На сле­ду­ю­щий день он от­пра­вил­ся об­рат­но в A со ско­ро­стью на 3 км/ч боль­ше преж­ней. По до­ро­ге он сде­лал оста­нов­ку на 3 часа. В ре­зуль­та­те ве­ло­си­пе­дист за­тра­тил на об­рат­ный путь столь­ко же вре­ме­ни, сколь­ко на путь из A в B. Най­ди­те ско­рость ве­ло­си­пе­ди­ста на пути из B в A. Ответ дайте в км/ч.

11. B 14 № 245174. Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 16

1. B 1 № 78793.

 

1 ки­ло­ватт-час элек­тро­энер­гии стоит 1 рубль 90 ко­пе­ек. Счет­чик элек­тро­энер­гии 1 июня по­ка­зы­вал 14700 ки­ло­ватт-часов, а 1 июля по­ка­зы­вал 14892 ки­ло­ватт-часа. Сколь­ко руб­лей нужно за­пла­тить за элек­тро­энер­гию за июнь?

2. B 2 № 263783.

На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена се­реб­ра, уста­нов­лен­ная Цен­тро­бан­ком РФ во все ра­бо­чие дни в ок­тяб­ре 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена се­реб­ра в руб­лях за грамм. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, ка­ко­го числа цена се­реб­ра была мак­си­маль­ной за дан­ный пе­ри­од.

3. B 3 № 77359. В ма­га­зи­не одеж­ды объ­яв­ле­на акция: если по­ку­па­тель при­об­ре­та­ет товар на сумму свыше 10 000 руб., он по­лу­ча­ет сер­ти­фи­кат на 1000 руб­лей, ко­то­рый можно об­ме­нять в том же ма­га­зи­не на любой товар ценой не выше 1000 руб. Если по­ку­па­тель участ­ву­ет в акции, он те­ря­ет право воз­вра­тить товар в ма­га­зин. По­ку­па­тель И. хочет при­об­ре­сти пи­джак ценой 9500 руб., ру­баш­ку ценой 800 руб. и гал­стук ценой 600 руб. В каком слу­чае И. за­пла­тит за по­куп­ку мень­ше всего:

 

1) И. купит все три то­ва­ра сразу.

2) И. купит сна­ча­ла пи­джак и ру­баш­ку, гал­стук по­лу­чит за сер­ти­фи­кат.

3) И. купит сна­ча­ла пи­джак и гал­стук, по­лу­чит ру­баш­ку за сер­ти­фи­кат.

 

В ответ за­пи­ши­те, сколь­ко руб­лей за­пла­тит И. за по­куп­ку в этом слу­чае.

 

4. B 4 № 27660. Най­ди­те ор­ди­на­ту точки пе­ре­се­че­ния оси Oy и от­рез­ка, со­еди­ня­ю­ще­го точки A(6; 8) и B(−6; 0).

5. B 5 № 1004. На эк­за­ме­не 40 во­про­сов, Коля не вы­учил 4 из них. Най­ди­те ве­ро­ят­ность того, что ему по­па­дет­ся вы­учен­ный во­прос.

6. B 6 № 315120. Най­ди­те ко­рень урав­не­ния .

7. B 7 № 53619. Най­ди­те сто­ро­ну пра­виль­но­го ше­сти­уголь­ни­ка, опи­сан­но­го около окруж­но­сти, ра­ди­ус ко­то­рой равен 

8. B 10 № 26820. Най­ди­те зна­че­ние вы­ра­же­ния , если .

9. B 11 № 42685. Для под­дер­жа­ния на­ве­са пла­ни­ру­ет­ся ис­поль­зо­вать ци­лин­дри­че­скую ко­лон­ну. Дав­ле­ние P (в пас­ка­лях), ока­зы­ва­е­мое на­ве­сом и ко­лон­ной на опору, опре­де­ля­ет­ся по фор­му­ле , где  кг — общая масса на­ве­са и ко­лон­ны, D — диа­метр ко­лон­ны (в мет­рах). Счи­тая уско­ре­ние сво­бод­но­го па­де­ния  м/с, а , опре­де­ли­те наи­мень­ший воз­мож­ный диа­метр ко­лон­ны, если дав­ле­ние, ока­зы­ва­е­мое на опору, не долж­но быть боль­ше 800 000 Па. Ответ вы­ра­зи­те в мет­рах.

10. B 13 № 99617. Даша и Маша про­па­лы­ва­ют гряд­ку за 12 минут, а одна Маша — за 20 минут. За сколь­ко минут про­па­лы­ва­ет гряд­ку одна Даша?

11. B 14 № 287103. Най­ди­те точку ми­ни­му­ма функ­ции .

 

           

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 17

1. B 1 № 77352. При опла­те услуг через пла­теж­ный тер­ми­нал взи­ма­ет­ся ко­мис­сия 5%. Тер­ми­нал при­ни­ма­ет суммы крат­ные 10 руб­лям. Аня хочет по­ло­жить на счет сво­е­го мо­биль­но­го те­ле­фо­на не мень­ше 300 руб­лей. Какую ми­ни­маль­ную сумму она долж­на по­ло­жить в при­ем­ное устрой­ство дан­но­го тер­ми­на­ла?

2. B 2 № 323024. На диа­грам­ме по­ка­за­но рас­пре­де­ле­ние вы­плав­ки меди в 10 стра­нах мира (в ты­ся­чах тонн) за 2006 год. Среди пред­став­лен­ных стран пер­вое место по вы­плав­ке меди за­ни­ма­ли США, де­ся­тое место — Ка­зах­стан. Какое место за­ни­ма­ла Ин­до­не­зия?

 

3. B 3 № 246261.

В сред­нем граж­да­нин А. в днев­ное время рас­хо­ду­ет 125 кВт  ч элек­тро­энер­гии в месяц, а в ноч­ное время — 155 кВт  ч элек­тро­энер­гии. Рань­ше у А. в квар­ти­ре был уста­нов­лен од­но­та­риф­ный счет­чик, и всю элек­тро­энер­гию он опла­чи­вал по та­ри­фу 2,6 руб. за кВт  ч. Год назад А. уста­но­вил двух­та­риф­ныйсчeтчик, при этом днев­ной рас­ход элек­тро­энер­гии опла­чи­ва­ет­ся по та­ри­фу 2,6 руб. за кВт  ч, а ноч­ной рас­ход опла­чи­ва­ет­ся по та­ри­фу 0,7 руб. за кВт  ч. В те­че­ние 12 ме­ся­цев режим по­треб­ле­ния и та­ри­фы опла­ты элек­тро­энер­гии не ме­ня­лись. На сколь­ко боль­ше за­пла­тил бы А. за этот пе­ри­од, если бы не по­ме­нял­ся счет­чик? Ответ дайте в руб­лях.

4. B 4 № 27582. Най­ди­те пло­щадь квад­ра­та, если его диа­го­наль равна 1.

5. B 5 № 1017. Аня с папой ре­ши­ли по­ка­тать­ся на ко­ле­се обо­зре­ния. Всего на ко­ле­се 22 ка­бин­ки, из них 5 — жел­тые, 6 — белые, осталь­ные — крас­ные. Ка­бин­ки по оче­ре­ди под­хо­дят к плат­фор­ме для по­сад­ки. Най­ди­те ве­ро­ят­ность того, что Аня про­ка­тит­ся в крас­ной ка­бин­ке.

6. B 6 № 39003.

 

Най­ди­те ко­рень урав­не­ния .

7. B 7 № 27364. В тре­уголь­ни­ке  угол  равен 90°, . Най­ди­те тан­генс внеш­не­го угла при вер­ши­не.

8. B 10 № 65765.

Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 505148. При адиа­ба­ти­че­ском про­цес­се для иде­аль­но­го газа вы­пол­ня­ет­ся закон pV^k = const , где p – дав­ле­ние в газе в пас­ка­лях, V – объём газа в ку­би­че­ских мет­рах. В ходе экс­пе­ри­мен­та с од­но­атом­ным иде­аль­ным газом (для него k = ) из на­чаль­но­го со­сто­я­ния, в ко­то­ром const = 3,2·10⁶Па·м⁴ , газ на­чи­на­ют сжи­мать. Какой наи­боль­ший объём V может за­ни­мать газ при дав­ле­нии p не ниже 2·10⁵ Па ? Ответ вы­ра­зи­те в ку­би­че­ских мет­рах.

10. B 13 № 505171. Мо­тор­ная лодка про­шла про­тив те­че­ния реки 135 км и вер­ну­лась в пункт от­прав­ле­ния, за­тра­тив на об­рат­ный путь на 6 часов мень­ше. Най­ди­те ско­рость те­че­ния, если ско­рость лодки в не­по­движ­ной воде равна 12 км/ч.

Ответ дайте в км/ч.

11. B 14 № 287103. Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 18

1. B 1 № 83343.

В доме, в ко­то­ром живет Оля, 9 эта­жей и не­сколь­ко подъ­ез­дов. На каж­дом этаже на­хо­дит­ся по 3 квар­ти­ры. Оля живет в квар­ти­ре № 32. В каком подъ­ез­де живет Оля?

2. B 2 № 28745.

На диа­грам­ме по­ка­за­но ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти во все дни с 10 по 29 но­яб­ря 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся дни ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство по­се­ти­те­лей сайта за дан­ный день. Опре­де­ли­те по диа­грам­ме, ка­ко­во наи­мень­шее су­точ­ное ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти за ука­зан­ный пе­ри­од.

3. B 3 № 18499. Для транс­пор­ти­ров­ки 3 тонн груза на 250 км можно вос­поль­зо­вать­ся услу­га­ми одной из трех фирм-пе­ре­воз­чи­ков. Сто­и­мость пе­ре­воз­ки и гру­зо­подъ­ем­ность ав­то­мо­би­лей для каж­до­го пе­ре­воз­чи­ка ука­за­на в таб­ли­це. Сколь­ко руб­лей при­дет­ся за­пла­тить за самую де­ше­вую пе­ре­воз­ку?

 

4. B 4 № 27948. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в квад­рат , счи­тая сто­ро­ны квад­рат­ных кле­ток рав­ны­ми .

5. B 5 № 505376. Перед на­ча­лом пер­во­го тура чем­пи­о­на­та по бад­мин­то­ну участ­ни­ков раз­би­ва­ют на иг­ро­вые пары слу­чай­ным об­ра­зом с по­мо­щью жре­бия. Всего в чем­пи­о­на­те участ­ву­ет 76 бад­мин­то­ни­стов, среди ко­то­рых 16 участ­ни­ков из Рос­сии, в том числе Игорь Чаев. Ка­ко­ва ве­ро­ят­ность того, что в пер­вом туре Игорь Чаев будет иг­рать с каким-либо бад­мин­то­ни­стом из Рос­сии?

6. B 6 № 101379.

Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

7. B 7 № 27615. Пло­щадь ромба равна 18. Одна из его диа­го­на­лей равна 12. Най­ди­те дру­гую диа­го­наль.

8. B 10 № 26849. Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 41117. При тем­пе­ра­ту­ре  рельс имеет длину  м. При воз­рас­та­нии тем­пе­ра­ту­ры про­ис­хо­дит теп­ло­вое рас­ши­ре­ние рель­са, и его длина, вы­ра­жен­ная в мет­рах, ме­ня­ет­ся по за­ко­ну, где  — ко­эф­фи­ци­ент теп­ло­во­го рас­ши­ре­ния,  — тем­пе­ра­ту­ра (в гра­ду­сах Цель­сия). При какой тем­пе­ра­ту­ре рельс удли­нит­ся на 7,5 мм? Ответ вы­ра­зи­те в гра­ду­сах Цель­сия.

10. B 13 № 99589. Из го­ро­дов  и , рас­сто­я­ние между ко­то­ры­ми равно 330 км, нав­стре­чу друг другу од­но­вре­мен­но вы­еха­ли два ав­то­мо­би­ля и встре­ти­лись через 3 часа на рас­сто­я­нии 180 км от го­ро­да . Най­ди­те ско­рость ав­то­мо­би­ля, вы­ехав­ше­го из го­ро­да . Ответ дайте в км/ч.

11. B 14 № 245177. Най­ди­те точку мак­си­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 19

1. B 1 № 24505.

Боль­но­му про­пи­са­но ле­кар­ство, ко­то­рое нужно пить по 0.5 г 4 раза в день в те­че­ние 3 дней. В одной упа­ков­ке 10 таб­ле­ток ле­кар­ства по 0.5 г. Ка­ко­го наи­мень­ше­го ко­ли­че­ства упа­ко­вок хва­тит на весь курс ле­че­ния?

2. B 2 № 26872. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена нефти на мо­мент за­кры­тия бир­же­вых тор­гов во все ра­бо­чие дни с 17 по 31 ав­гу­ста 2004 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена бар­ре­ля нефти в дол­ла­рах США. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку наи­мень­шую цену нефти на мо­мент за­кры­тия тор­гов в ука­зан­ный пе­ри­од (в дол­ла­рах США за бар­рель).

 

 

3. B 3 № 26685. В таб­ли­це даны та­ри­фы на услу­ги трех фирм такси. Пред­по­ла­га­ет­ся по­езд­ка дли­тель­но­стью 70 минут. Нужно вы­брать фирму, в ко­то­рой заказ будет сто­ить де­шев­ле всего. Сколь­ко руб­лей будет сто­ить этот заказ?

 

 

*Если по­езд­ка про­дол­жа­ет­ся мень­ше ука­зан­но­го вре­ме­ни, она опла­чи­ва­ет­ся по сто­и­мо­сти ми­ни­маль­ной по­езд­ки.

4. B 4 № 27743. В тре­уголь­ни­ке  угол  равен , внеш­ний угол при вер­ши­не  равен . Най­ди­те угол . Ответ дайте в гра­ду­сах.

5. B 5 № 320178. На кла­ви­а­ту­ре те­ле­фо­на 10 цифр, от 0 до 9. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но на­жа­тая цифра будет чётной?

6. B 6 № 77372. Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

 

7. B 7 № 27808. Диа­го­наль па­рал­ле­ло­грам­ма об­ра­зу­ет с двумя его сто­ро­на­ми углы  и . Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма. Ответ дайте в гра­ду­сах.

8. B 10 № 68595.

Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 263861. Рас­сто­я­ние от на­блю­да­те­ля, на­хо­дя­ще­го­ся на не­боль­шой вы­со­те  ки­ло­мет­ров над землeй, до на­блю­да­е­мой им линии го­ри­зон­та вы­чис­ля­ет­ся по фор­му­ле , где (км) — ра­ди­ус Земли. С какой вы­со­ты го­ри­зонт виден на рас­сто­я­нии 28 ки­ло­мет­ров? Ответ вы­ра­зи­те в ки­ло­мет­рах.

10. B 13 № 26596. Двое ра­бо­чих, ра­бо­тая вме­сте, могут вы­пол­нить ра­бо­ту за 12 дней. За сколь­ко дней, ра­бо­тая от­дель­но, вы­пол­нит эту ра­бо­ту пер­вый ра­бо­чий, если он за два дня вы­пол­ня­ет такую же часть ра­бо­ты, какую вто­рой – за три дня?

11. B 14 № 245174. Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 20

1. B 1 № 26644. Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. После удер­жа­ния на­ло­га на до­хо­ды Мария Кон­стан­ти­нов­на по­лу­чи­ла 9570 руб­лей. Сколь­ко руб­лей со­став­ля­ет за­ра­бот­ная плата Марии Кон­стан­ти­нов­ны?

 

 

2. B 2 № 263767.

На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена пла­ти­ны, уста­нов­лен­ная Цен­тро­бан­ком РФ во все ра­бо­чие дни во все ра­бо­чие дни с 1 по 27 ок­тяб­ря 2010 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена пла­ти­ны в руб­лях за грамм. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку наи­боль­шую цену пла­ти­ны в пе­ри­од с 1 по 13 ок­тяб­ря. Ответ дайте в руб­лях за грамм.

3. B 3 № 18435.

 

В таб­ли­це даны усло­вия бан­ков­ско­го вкла­да в трех раз­лич­ных бан­ках. Пред­по­ла­га­ет­ся, что кли­ент кла­дет на счет 40000 руб­лей на срок 1 год. В каком банке к концу года вклад ока­жет­ся наи­боль­шим? В от­ве­те ука­жи­те сумму этого вкла­да в руб­лях.

 

Банк	Об­слу­жи­ва­ние счета*	Про­цент­ная став­ка  (% го­до­вых)**
Банк А	30 руб. в год	2,3
Банк Б	9 руб. в месяц	2,5
Банк В	Бес­плат­но	2,2

 

* В на­ча­ле года или ме­ся­ца со счета сни­ма­ет­ся ука­зан­ная сумма в упла­ту за ве­де­ние счета

 ** В конце года вклад уве­ли­чи­ва­ет­ся на ука­зан­ное ко­ли­че­ство про­цен­тов.

4. B 4 № 27943. К окруж­но­сти, впи­сан­ной в тре­уголь­ник ABC, про­ве­де­ны три ка­са­тель­ные. Пе­ри­мет­ры от­се­чен­ных тре­уголь­ни­ков равны 6, 8, 10. Най­ди­те пе­ри­метр дан­но­го тре­уголь­ни­ка.

5. B 5 № 54903.

Най­ди­те диа­го­наль квад­ра­та, если его пло­щадь равна 364,5.

6. B 6 № 3231.

Най­ди­те ко­рень урав­не­ния .

7. B 7 № 27873. Точки , , , , рас­по­ло­жен­ные на окруж­но­сти, делят эту окруж­ность на че­ты­ре дуги , ,  и , гра­дус­ные ве­ли­чи­ны ко­то­рых от­но­сят­ся со­от­вет­ствен­но как . Най­ди­те угол  че­ты­рех­уголь­ни­ка . Ответ дайте в гра­ду­сах.

8. B 10 № 77398. Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 54799.

Ко­эф­фи­ци­ент по­лез­но­го дей­ствия (КПД) не­ко­то­ро­го дви­га­те­ля опре­де­ля­ет­ся фор­му­лой , где  — тем­пе­ра­ту­ра на­гре­ва­те­ля (в гра­ду­сах Кель­ви­на),  — тем­пе­ра­ту­ра хо­ло­диль­ни­ка (в гра­ду­сах Кель­ви­на). При какой ми­ни­маль­ной тем­пе­ра­ту­ре на­гре­ва­те­ля  КПД этого дви­га­те­ля будет не мень­ше , если тем­пе­ра­ту­ра хо­ло­диль­ни­ка  К? Ответ вы­ра­зи­те в гра­ду­сах Кель­ви­на.

10. B 13 № 26600. Пер­вая труба про­пус­ка­ет на 5 лит­ров воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет вто­рая труба, если ре­зер­ву­ар объ­е­мом 375 лит­ров она за­пол­ня­ет на 10 минут быст­рее, чем пер­вая труба за­пол­ня­ет ре­зер­ву­ар объ­е­мом 500 лит­ров?

11. B 14 № 245184. Най­ди­те наи­боль­шее зна­че­ние функ­ции 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 21

1. B 1 № 505392. Каж­дый день во время кон­фе­рен­ции рас­хо­ду­ет­ся 80 па­ке­ти­ков чая. Кон­фе­рен­ция длит­ся 4 дня. Чай продаётся в пач­ках по 100 па­ке­ти­ков. Сколь­ко пачек чая нужно ку­пить на все дни кон­фе­рен­ции?

2. B 2 № 263677.

На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­зан курс дол­ла­ра, уста­нов­лен­ный Цен­тро­бан­ком РФ, во все ра­бо­чие дни с 22 сен­тяб­ря по 22 ок­тяб­ря 2010 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена дол­ла­ра в руб­лях. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку наи­мень­ший курс дол­ла­ра за ука­зан­ный пе­ри­од. Ответ дайте в руб­лях.

3. B 3 № 40291.

Стро­и­тель­ной фирме нужно при­об­ре­сти 80 ку­бо­мет­ров пе­но­бе­то­на у од­но­го из трех по­став­щи­ков. Цены и усло­вия до­став­ки при­ве­де­ны в таб­ли­це. Сколь­ко руб­лей при­дет­ся за­пла­тить за самую де­ше­вую по­куп­ку с до­став­кой?

4. B 4 № 27767. В тре­уголь­ни­ке   – вы­со­та,  – бис­сек­три­са,  – точка пе­ре­се­че­ния  и  угол  равен . Най­ди­те угол . Ответ дайте в гра­ду­сах.

5. B 5 № 1018. Ки­рилл с папой решил по­ка­тать­ся на ко­ле­се обо­зре­ния. Всего на ко­ле­се 30 ка­би­нок, из них 8 – фи­о­ле­то­вые, 4 – зе­ле­ные, осталь­ные – оран­же­вые. Ка­бин­ки по оче­ре­ди под­хо­дят к плат­фор­ме для по­сад­ки. Най­ди­те ве­ро­ят­ность того, что Ки­рилл про­ка­тит­ся в оран­же­вой ка­бин­ке.

 

6. B 6 № 14673.

Най­ди­те ко­рень урав­не­ния: 

7. B 7 № 27251. В тре­уголь­ни­ке  угол  равен 90°, , . Най­ди­те .

8. B 10 № 26831. Най­ди­те зна­че­ние вы­ра­же­ния  при .

9. B 11 № 42215. Ко­эф­фи­ци­ент по­лез­но­го дей­ствия (КПД) кор­мо­за­пар­ни­ка равен от­но­ше­нию ко­ли­че­ства теп­ло­ты, за­тра­чен­но­го на на­гре­ва­ние воды мас­сой  (в ки­ло­грам­мах) от тем­пе­ра­ту­ры  до тем­пе­ра­ту­ры  (в гра­ду­сах Цель­сия) к ко­ли­че­ству теп­ло­ты, по­лу­чен­но­му от сжи­га­ния дров массы  кг. Он опре­де­ля­ет­ся фор­му­лой , где  Дж/(кгК) — теп­ло­ем­кость воды,  Дж/кг — удель­ная теп­ло­та сго­ра­ния дров. Опре­де­ли­те наи­мень­шее ко­ли­че­ство дров, ко­то­рое по­на­до­бит­ся сжечь в кор­мо­за­пар­ни­ке, чтобы на­греть  кг воды от  до ки­пе­ния, если из­вест­но, что КПД кор­мо­за­пар­ни­ка не боль­ше . Ответ вы­ра­зи­те в ки­ло­грам­мах.

10. B 13 № 6005. Катер в 11:00 вышел из пунк­та А в пункт В, рас­по­ло­жен­ный в 30 км от А. Про­быв в пунк­те В 2 часа 40 минут, катер от­пра­вил­ся назад и вер­нул­ся в пункт А в 19:00. Опре­де­ли­те (в км/час) ско­рость те­че­ния реки, если из­вест­но, что соб­ствен­ная ско­рость ка­те­ра равна 12 км/ч.

 

 

11. B 14 № 287303.

Най­ди­те наи­боль­шее зна­че­ние функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 22

1. B 1 № 77356. Спи­до­метр ав­то­мо­би­ля по­ка­зы­ва­ет ско­рость в милях в час. Какую ско­рость (в милях в час) по­ка­зы­ва­ет спи­до­метр, если ав­то­мо­биль дви­жет­ся со ско­ро­стью 36 км в час? (Счи­тай­те, что 1 миля равна 1,6 км.)

2. B 2 № 323071. На диа­грам­ме по­ка­за­но рас­пре­де­ле­ние вы­плав­ки цинка в 11 стра­нах мира (в ты­ся­чах тонн) за 2009 год. Среди пред­став­лен­ных стран пер­вое место по вы­плав­ке меди за­ни­ма­ло Ма­рок­ко, один­на­дца­тое место — Бол­га­рия. Какое место за­ни­ма­ла КНДР?

 

3. B 3 № 18763.

Для того, чтобы свя­зать сви­тер, хо­зяй­ке нужно 800 грам­мов шер­сти крас­но­го цвета. Можно ку­пить крас­ную пряжу по цене 80 руб­лей за 100 г, а можно ку­пить не­окра­шен­ную пряжу по цене 50 руб­лей за 100 г и окра­сить ее. Один па­ке­тик крас­ки стоит 20 руб­лей и рас­счи­тан на окрас­ку 400 г пряжи. Какой ва­ри­ант по­куп­ки де­шев­ле? В ответ на­пи­ши­те, сколь­ко руб­лей будет сто­ить эта по­куп­ка.

4. B 4 № 248809.

Най­ди­те пло­щадь квад­ра­та, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

5. B 5 № 1009. Люба вклю­ча­ет те­ле­ви­зор. Те­ле­ви­зор вклю­ча­ет­ся на слу­чай­ном ка­на­ле. В это время по шести ка­на­лам из со­ро­ка вось­ми по­ка­зы­ва­ют до­ку­мен­таль­ные филь­мы. Най­ди­те ве­ро­ят­ность того, что Люба по­па­дет на канал, где до­ку­мен­таль­ные филь­мы не идут.

6. B 6 № 38183.

Най­ди­те ко­рень урав­не­ния .

7. B 7 № 27272. В тре­уголь­ни­ке  угол  равен 90°,  – вы­со­та, , . Най­ди­те .

8. B 10 № 26862. Най­ди­те зна­че­ние вы­ра­же­ния .

 

 

 

 

9. B 11 № 42377. При сбли­же­нии ис­точ­ни­ка и при­ем­ни­ка зву­ко­вых сиг­на­лов дви­жу­щих­ся в не­ко­то­рой среде по пря­мой нав­стре­чу друг другу ча­сто­та зву­ко­во­го сиг­на­ла, ре­ги­стри­ру­е­мо­го приeмни­ком, не сов­па­да­ет с ча­сто­той ис­ход­но­го сиг­на­ла  Гц и опре­де­ля­ет­ся сле­ду­ю­щим вы­ра­же­ни­ем:  (Гц), где c — ско­рость рас­про­стра­не­ния сиг­на­ла в среде (в м/с), а  м/с и  м/с — ско­ро­сти приeмника и ис­точ­ни­ка от­но­си­тель­но среды со­от­вет­ствен­но. При какой мак­си­маль­ной ско­ро­сти c (в м/с) рас­про­стра­не­ния сиг­на­ла в среде ча­сто­та сиг­на­ла в приeмнике f будет не менее 135 Гц?

10. B 13 № 115353. Первую треть трас­сы ав­то­мо­биль ехал со ско­ро­стью 90 км/ч, вто­рую треть — со ско­ро­стью 120 км/ч, а по­след­нюю — со ско­ро­стью 45 км/ч. Най­ди­те сред­нюю ско­рость ав­то­мо­би­ля на про­тя­же­нии всего пути. Ответ дайте в км/ч.

11. B 14 № 245178. Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 23

1. B 1 № 82081.

 

В сен­тяб­ре 1 кг ви­но­гра­да стоил 90 руб­лей, в ок­тяб­ре ви­но­град по­до­ро­жал на 25%, а в но­яб­ре еще на 20%. Сколь­ко руб­лей стоил 1 кг ви­но­гра­да после по­до­ро­жа­ния в но­яб­ре?

2. B 2 № 263863. Когда са­мо­лет на­хо­дит­ся в го­ри­зон­таль­ном по­ле­те, подъ­ем­ная сила, дей­ству­ю­щая на кры­лья, за­ви­сит толь­ко от ско­ро­сти. На ри­сун­ке изоб­ра­же­на эта за­ви­си­мость для не­ко­то­ро­го са­мо­ле­та. На оси абс­цисс от­кла­ды­ва­ет­ся ско­рость (в ки­ло­мет­рах в час), на оси ор­ди­нат — сила (в тон­нах силы). Опре­де­ли­те по ри­сун­ку, чему равна подъ­ем­ная сила (в тон­нах силы) при ско­ро­сти 200 км/ч?

3. B 3 № 245761.

В таб­ли­це ука­за­ны сред­ние цены (в руб­лях) на не­ко­то­рые ос­нов­ные про­дук­ты пи­та­ния в трех го­ро­дах Рос­сии (по дан­ным на на­ча­ло 2010 года).

 

 

Опре­де­ли­те, в каком из этих го­ро­дов ока­жет­ся самым де­ше­вым сле­ду­ю­щий набор про­дук­тов: 2 ба­то­на пше­нич­но­го хлеба, 2 кг го­вя­ди­ны, 1 л под­сол­неч­но­го масла. В ответ за­пи­ши­те сто­и­мость дан­но­го на­бо­ра про­дук­тов в этом го­ро­де (в руб­лях).

4. B 4 № 48913. В тре­уголь­ни­ке ABC , вы­со­та AH равна 42. Най­ди­те угол C. Ответ дайте в гра­ду­сах.

5. B 5 № 320183. Перед на­ча­лом фут­боль­но­го матча судья бро­са­ет мо­нет­ку, чтобы опре­де­лить, какая из ко­манд начнёт игру с мячом. Ко­ман­да «Физик» иг­ра­ет три матча с раз­ны­ми ко­ман­да­ми. Най­ди­те ве­ро­ят­ность того, что в этих играх «Физик» вы­иг­ра­ет жре­бий ровно два раза.

6. B 6 № 26651. Най­ди­те ко­рень урав­не­ния .

7. B 7 № 27296. В тре­уголь­ни­ке  , , . Най­ди­те вы­со­ту .

8. B 10 № 62203. Най­ди­те зна­че­ние вы­ра­же­ния .

9. B 11 № 27992. Урав­не­ние про­цес­са, в ко­то­ром участ­во­вал газ, за­пи­сы­ва­ет­ся в виде, где  (Па) – дав­ле­ние в газе,  – объeм газа в ку­би­че­ских мет­рах, a – по­ло­жи­тель­ная кон­стан­та. При каком наи­мень­шем зна­че­нии кон­стан­ты a умень­ше­ние вдвое раз объeма газа, участ­ву­ю­ще­го в этом про­цес­се, при­во­дит к уве­ли­че­нию дав­ле­ния не менее, чем в 4 раза?

10. B 13 № 39799. Двое ра­бо­чих, ра­бо­тая вме­сте, могут вы­пол­нить ра­бо­ту за 2 дня. За сколь­ко дней, ра­бо­тая от­дель­но, вы­пол­нит эту ра­бо­ту пер­вый ра­бо­чий, если он за 1 день вы­пол­ня­ет такую же часть ра­бо­ты, какую вто­рой — за 2 дня?

11. B 14 № 245176. Най­ди­те наи­боль­шее зна­че­ние функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 24

1. B 1 № 25279.

Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. За­ра­бот­ная плата Ивана Кузь­ми­ча равна 13 000 руб­лей. Сколь­ко руб­лей он по­лу­чит после вы­че­та на­ло­га на до­хо­ды?

2. B 2 № 77261.

На диа­грам­ме по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра воз­ду­ха в Ниж­нем Нов­го­ро­де (Горь­ком) за каж­дый месяц 1994 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся ме­ся­цы, по вер­ти­ка­ли — тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Опре­де­ли­те по диа­грам­ме, сколь­ко было ме­ся­цев, когда сред­не­ме­сяч­ная тем­пе­ра­ту­ра пре­вы­ша­ла 4 гра­ду­са Цель­сия.

3. B 3 № 18431.

 

В таб­ли­це даны усло­вия бан­ков­ско­го вкла­да в трех раз­лич­ных бан­ках. Пред­по­ла­га­ет­ся, что кли­ент кла­дет на счет 10000 руб­лей на срок 1 год. В каком банке к концу года вклад ока­жет­ся наи­боль­шим? В от­ве­те ука­жи­те сумму этого вкла­да в руб­лях.

 

Банк	Об­слу­жи­ва­ние счета*	Про­цент­ная став­ка  (% го­до­вых)**
Банк А	30 руб. в год	1,9
Банк Б	9 руб. в месяц	2,2
Банк В	Бес­плат­но	1

 

* В на­ча­ле года или ме­ся­ца со счета сни­ма­ет­ся ука­зан­ная сумма в упла­ту за ве­де­ние счета

 

** В конце года вклад уве­ли­чи­ва­ет­ся на ука­зан­ное ко­ли­че­ство про­цен­тов.

4. B 4 № 27715. Диа­го­на­ли ромба  равны 12 и 16. Най­ди­те длину век­то­ра .

 

5. B 5 № 55153.

Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна 99. Один из его ка­те­тов равен 33. Най­ди­те дру­гой катет.

6. B 6 № 99757.

Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

7. B 7 № 27248. В тре­уголь­ни­ке  угол  равен 90°, , . Най­ди­те .

8. B 10 № 26887. Най­ди­те зна­че­ние вы­ра­же­ния 

9. B 11 № 505382. Рас­сто­я­ние от на­блю­да­те­ля, на­хо­дя­ще­го­ся на не­боль­шой вы­со­те  ки­ло­мет­ров над землёй, до на­блю­да­е­мой им линии го­ри­зон­та вы­чис­ля­ет­ся по фор­му­ле  где  — ра­ди­ус Земли. С какой вы­со­ты го­ри­зонт виден на рас­сто­я­нии 160 ки­ло­мет­ров? Ответ вы­ра­зи­те в ки­ло­мет­рах.

10. B 13 № 117235. По морю па­рал­лель­ны­ми кур­са­ми в одном на­прав­ле­нии сле­ду­ют два су­хо­гру­за: пер­вый дли­ной 140 мет­ров, вто­рой — дли­ной 60 мет­ров. Сна­ча­ла вто­рой су­хо­груз от­ста­ет от пер­во­го, и в не­ко­то­рый мо­мент вре­ме­ни рас­сто­я­ние от кормы пер­во­го су­хо­гру­за до носа вто­ро­го со­став­ля­ет 200 мет­ров. Через 15 минут после этого уже пер­вый су­хо­груз от­ста­ет от вто­ро­го так, что рас­сто­я­ние от кормы вто­ро­го су­хо­гру­за до носа пер­во­го равно 100 мет­рам. На сколь­ко ки­ло­мет­ров в час ско­рость пер­во­го су­хо­гру­за мень­ше ско­ро­сти вто­ро­го?

11. B 14 № 286703.

Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

Вариант № 25

1. B 1 № 505456. Боль­но­му про­пи­са­но ле­кар­ство, ко­то­рое нужно при­ни­мать по 0,5 г 2 раза в день в те­че­ние 7 дней. В одной упа­ков­ке 10 таб­ле­ток по 0,25г. Ка­ко­го наи­мень­ше­го ко­ли­че­ства упа­ко­вок хва­тит на весь курс ле­че­ния?

2. B 2 № 28743.

На диа­грам­ме по­ка­за­но ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти во все дни с 10 по 29 но­яб­ря 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся дни ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство по­се­ти­те­лей сайта за дан­ный день. Опре­де­ли­те по диа­грам­ме, сколь­ко было дней за дан­ный пе­ри­од, когда на сайте РИА Но­во­сти было менее по­лу­мил­ли­о­на по­се­ти­те­лей.

 

3. B 3 № 77360. В ма­га­зи­не одеж­ды объ­яв­ле­на акция: если по­ку­па­тель при­об­ре­та­ет товар на сумму свыше 10 000 руб., он по­лу­ча­ет скид­ку на сле­ду­ю­щую по­куп­ку в раз­ме­ре 10%. Если по­ку­па­тель участ­ву­ет в акции, он те­ря­ет право воз­вра­тить товар в ма­га­зин. По­ку­па­тель Б. хочет при­об­ре­сти курт­ку ценой 9300 руб., ру­баш­ку ценой 1800 руб. и пер­чат­ки ценой 1200 руб. В каком слу­чае Б. за­пла­тит за по­куп­ку мень­ше всего:

1) Б. купит все три то­ва­ра сразу.

2) Б. купит сна­ча­ла курт­ку и ру­баш­ку, а потом пер­чат­ки со скид­кой.

3) Б. купит сна­ча­ла курт­ку и пер­чат­ки, а потом ру­баш­ку со скид­кой.

В ответ за­пи­ши­те, сколь­ко руб­лей за­пла­тит Б. за по­куп­ку в этом слу­чае.

4. B 4 № 27582. Най­ди­те пло­щадь квад­ра­та, если его диа­го­наль равна 1.

5. B 5 № 322497. В кар­ма­не у Коли было че­ты­ре кон­фе­ты — «Гри­льяж», «Ла­сточ­ка», «Взлётная» и «Василёк», а так же ключи от квар­ти­ры. Вы­ни­мая ключи, Коля слу­чай­но вы­ро­нил из кар­ма­на одну кон­фе­ту. Най­ди­те ве­ро­ят­ность того, что по­те­ря­лась кон­фе­та «Ла­сточ­ка».

6. B 6 № 26658. Най­ди­те ко­рень урав­не­ния .

7. B 7 № 27424. В тре­уголь­ни­ке  , . Най­ди­те тан­генс внеш­не­го угла при вер­ши­не .

8. B 10 № 65919. Най­ди­те , если  при 

9. B 11 № 41987.

По за­ко­ну Ома для пол­ной цепи сила тока, из­ме­ря­е­мая в ам­пе­рах, равна , где  — ЭДС ис­точ­ни­ка (в воль­тах),  Ом — его внут­рен­нее со­про­тив­ле­ние,  — со­про­тив­ле­ние цепи (в омах). При каком наи­мень­шем со­про­тив­ле­нии цепи сила тока будет со­став­лять не более  от силы тока ко­рот­ко­го за­мы­ка­ния ? (Ответ вы­ра­зи­те в омах.)

10. B 13 № 99607. Пер­вые 190 км ав­то­мо­биль ехал со ско­ро­стью 50 км/ч, сле­ду­ю­щие 180 км — со ско­ро­стью 90 км/ч, а затем 170 км — со ско­ро­стью 100 км/ч. Най­ди­те сред­нюю ско­рость ав­то­мо­би­ля на про­тя­же­нии всего пути. Ответ дайте в км/ч.

11. B 14 № 245177. Най­ди­те точку мак­си­му­ма функ­ции .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант № 26

1.  Роз­нич­ная цена учеб­ни­ка 180 руб­лей, она на 20% выше опто­вой цены. Какое наи­боль­шее число таких учеб­ни­ков можно ку­пить по опто­вой цене на 7900 руб­лей?

2. На диа­грам­ме по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра воз­ду­ха в Санкт-Пе­тер­бур­ге за каж­дый месяц 1999 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся ме­ся­цы, по вер­ти­ка­ли - тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Опре­де­ли­те по диа­грам­ме наи­боль­шую сред­не­ме­сяч­ную тем­пе­ра­ту­ру в пе­ри­од с ян­ва­ря по май 1999 года. Ответ дайте в гра­ду­сах Цель­сия.

 

3. В таб­ли­це даны усло­вия бан­ков­ско­го вкла­да в трех раз­лич­ных бан­ках. Пред­по­ла­га­ет­ся, что кли­ент кла­дет на счет 40000 руб­лей на срок 1 год. В каком банке к концу года вклад ока­жет­ся наи­боль­шим? В от­ве­те ука­жи­те сумму этого вкла­да в руб­лях.

 

Банк	Об­слу­жи­ва­ние счета*	Про­цент­ная став­ка  (% го­до­вых)**
Банк А	30 руб. в год	2,4
Банк Б	9 руб. в месяц	2,5
Банк В	Бес­плат­но	1,7

 

* В на­ча­ле года или ме­ся­ца со счета сни­ма­ет­ся ука­зан­ная сумма в упла­ту за ве­де­ние счета

 

** В конце года вклад уве­ли­чи­ва­ет­ся на ука­зан­ное ко­ли­че­ство про­цен­тов.

4. Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

 

5. В клас­се 26 че­ло­век, среди них два близ­не­ца — Ан­дрей и Сер­гей. Класс слу­чай­ным об­ра­зом делят на две груп­пы по 13 че­ло­век в каж­дой. Най­ди­те ве­ро­ят­ность того, что Ан­дрей и Сер­гей ока­жут­ся в одной груп­пе.

6. Ре­ши­те урав­не­ние . В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.

7. В тре­уголь­ни­ке  угол  равен 90°, угол равен , . Най­ди­те .

10. Най­ди­те зна­че­ние вы­ра­же­ния .

11. Ам­пли­ту­да ко­ле­ба­ний ма­ят­ни­ка за­ви­сит от ча­сто­ты вы­нуж­да­ю­щей силы, опре­де­ля­е­мой по фор­му­ле , где  – ча­сто­та вы­нуж­да­ю­щей силы (в ),  – по­сто­ян­ный па­ра­метр,  – ре­зо­нанс­ная ча­сто­та. Най­ди­те мак­си­маль­ную ча­сто­ту , мень­шую ре­зо­нанс­ной, для ко­то­рой ам­пли­ту­да ко­ле­ба­ний пре­вос­хо­дит ве­ли­чи­ну  не более чем на . Ответ вы­ра­зи­те в .

13. № 109059. Сме­ша­ли 8 лит­ров 25-про­цент­но­го вод­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с 12 лит­ра­ми 20-про­цент­но­го вод­но­го рас­тво­ра этого же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

14. Най­ди­те наи­боль­шее зна­че­ние функ­ции .

 

 

 

 

 

 

 

 

Пакет преподавателя

Показатели оценки результатов освоения программы учебной дисциплины:

 

 

Вариант № 1
№ п/п	№ задания	Ответ
1	77346	20
2	27523	4
3	246381	449,5
4	58749	4
5	1007	0,9
6	77373	-2,5
7	29575	20
8	26859	0
9	54799	500
10	39257	11
11	245184	9

 

Вариант № 2
№ п/п	№ задания	Ответ
1	80181	62,7
2	26875	10
3	5551	180
4	244995	3
5	320184	4
6	26651	4
7	27305	0,28
8	69155	1
9	41691	3
10	26593	13
11	287503	-15

 

Вариант № 3
п/п	№ задания	Ответ
1	504246	4
2	27529	3
3	26683	2,5
4	27649	8
5	1016	0,4
6	3185	20
7	27871	122
8	26749	20
9	41987	9
10	26597	10
11	287103	15

 

Вариант № 4
п/п	№ задания	Ответ
1	77342	57
2	27510	6
3	505395	20200
4	27596	0,25
5	283477	0,125
6	3185	20
7	27899	8
8	69485	144
9	41493	4
10	99605	88
11	505151	6

 

Вариант № 5
1	26621	6
2	27518	16|16,0
3	41085	198900
4	248697	2
5	320189	0,498
6	26665	5
7	27363	-0,1
8	77418	3
9	27970	36
10	506102	5
11	287303	-7

 

Вариант № 6
№ п/п	№ задания	Ответ
1	26643	10875
2	263977	80
3	26679	178200
4	5255	14
5	286119	0,2
6	13687	-5
7	27445	0,5
8	26827	3,5
9	41313	7
10	39507	11
11	286903	13

 

Вариант № 7
№ п/п	№ задания	Ответ
1	26632	10800
2	28763	3
3	505374	12660
4	244991	5
5	286381	0,4
6	77368	-1,5
7	27843	0,5
8	26811	-25
9	27953	25
10	107387	44908
11	287203	7

 

Вариант № 8
№ п/п	№ задания	Ответ
1	282957	269,6
2	5373	14
3	26685	1230
4	27603	18
5	321399	0,4
6	100787	-6
7	51343	58
8	26883	9
9	41471	110
10	99597	25
11	287703	4
Вариант № 9
№ п/п	№ задания	Ответ
1	26633	1160
2	77255	25000
3	77363	560
4	27453	-2
5	285927	0,6
6	103019	5
7	282851	29
8	66653	1
9	41955	3,5
10	39633	16
11	287103	15

 

Вариант № 10
№ п/п	№ задания	Ответ
1	26618	8
2	263799	7
3	26683	2,5
4	322727	6
5	504533	0,2
6	505398	-3
7	27237	4
8	92055	6
9	42739	25
10	505447	100
11	245175	2

 

Вариант № 11
№ п/п	№ задания	Ответ
1	77343	1296
2	263597	19
3	18759	340
4	505459	3
5	1012	0,25
6	104691	-2
7	27400	0,1
8	96369	900
9	41691	3
10	99591	70
11	245179	2

 

Вариант № 12
№ п/п	№ задания	Ответ
1	83785	5
2	26876	3|3,0
3	18759	340
4	27705	36
5	320851	0,4
6	26655	12,5
7	30465	25,2
8	87483	31
9	27972	4
10	112517	60
11	245183	16
Вариант № 13
№ п/п	№ задания	Ответ
1	77344	400
2	27516	-2
3	5453	1424,5
4	48913	30
5	315953	0,375
6	27466	31
7	245385	30
8	77393	0,0001
9	43097	3,5
10	26600	25
11	245181	3

 

Вариант № 14
№ п/п	№ задания	Ответ
1	26643	10875
2	263995	60
3	319857	25
4	245003	1
5	321035	0,375
6	13375	-1
7	27220	0,1
8	77393	0,0001
9	42831	30
10	6005	3
11	287703	4

 

Вариант № 15
№ п/п	№ задания	Ответ
1	323516	474
2	263865	12
3	41085	198900
4	27811	10
5	1015	0,15
6	13687	-5
7	27917	1,5
8	92555	225
9	42519	180000
10	26581	10
11	245174	3

 

Вариант № 16
№ п/п	№ задания	Ответ
1	78793	364,8
2	263783	15
3	77359	10100
4	27660	4
5	1004	0,9
6	315120	2
7	53619	94
8	26820	-12
9	42685	0,2
10	99617	30
11	287103	15
Вариант № 17
№ п/п	№ задания	Ответ
1	77352	320
2	323024	5
3	246261	3534
4	27582	0,5
5	1017	0,5
6	39003	226
7	27364	-0,25
8	65765	62,5
9	505148	8
10	505171	3
11	287103	15

 

Вариант № 18
№ п/п	№ задания	Ответ
1	83343	2
2	28745	400000
3	18499	4000
4	27948	2
5	505376	0,2
6	101379	-6,5
7	27615	3
8	26849	-3
9	41117	62,5
10	99589	50
11	245177	1

 

Вариант № 19
№ п/п	№ задания	Ответ
1	24505	2
2	26872	39
3	26685	1230
4	27743	62
5	320178	0,5
6	77372	1
7	27808	120
8	68595	-1
9	263861	0,06125
10	26596	20
11	245174	3

 

Вариант № 20
№ п/п	№ задания	Ответ
1	26644	11000
2	263767	1645
3	18435	40889,31
4	27943	24
5	54903	27
6	3231	-13
7	27873	60
8	77398	7
9	54799	500
10	26600	25
11	245184	9
Вариант № 21
№ п/п	№ задания	Ответ
1	505392	4
2	263677	29,6
3	40291	240900
4	27767	116
5	1018	0,6
6	14673	733
7	27251	0,28
8	26831	6
9	42215	21
10	6005	3
11	287303	-7

 

Вариант № 22
№ п/п	№ задания	Ответ
1	77356	22,5
2	323071	4
3	18763	440
4	248809	37
5	1009	0,875
6	38183	4
7	27272	4,8
8	26862	16
9	42377	821
10	115353	72
11	245178	3

 

Вариант № 23
№ п/п	№ задания	Ответ
1	82081	135
2	263863	1
3	245761	620
4	48913	30
5	320183	0,375
6	26651	4
7	27296	2
8	62203	3
9	27992	2
10	39799	3
11	245176	3

 

Вариант № 24
№ п/п	№ задания	Ответ
1	25279	11310
2	77261	7
3	18431	10159,43
4	27715	12
5	55153	6
6	99757	2
7	27248	7
8	26887	2
9	505382	2
10	117235	2
11	286703	14

 

 

 

Вариант № 25
№ п/п	№ задания	Ответ
1	505456	3
2	28743	3
3	77360	12120
4	27582	0,5
5	322497	0,25
6	26658	-42
7	27424	-0,25
8	65919	0
9	41987	9
10	99607	72
11	245177	1

 

Вариант № 26
№ п/п	№ задания	Ответ
1	77147	52
2	77251	8
3	18425	40929,28
4	244997	1,5
5	320192	0,48
6	104015	4
7	27783	2
8	77398	7
9	27974	120
10	109059	22
11	287703	4

 

 

 

Шкала оценки образовательных достижений

 

Количество правильных ответов	Оценка уровня подготовки
	балл (отметка)	вербальный аналог
10,11 заданий	5	отлично
8,9 заданий	4	хорошо
6,7 заданий	3	удовлетворительно
1-5 заданий	2	неудовлетворительно

 

 

 

 

 

Контроль проверяемых умений и знаний: У1, З1,З2, З3, З4

осуществляется по результатам выполнения практических заданий:

 

	Форма контроля	Приложения к КОС
Раздел 1. Элементы логики	Практическая работа №№1-4	Методические рекомендации по организации и проведению практических занятий для студентов
Раздел 2. Натуральные числа и нуль	Практическая работа  №5-10	Методические рекомендации по организации и проведению практических занятий для студентов
Раздел 3. Геометрические фигуры	Практическая работа №11-14	Методические рекомендации по организации и проведению практических занятий для студентов

 

 

 

 

 

 

 

 

 

 

Раздел 1. Элементы логики.

Тема 1.1. Множества и операции над множествами

Вопросы к изучению

1.     Понятие множества и элемента множества.

2.     Пустое множество. Способы задания множеств.

3.     Отношения между множествами: включение, равенство, пересечение. Подмножество.

4.       Изображение отношений между множествами при помощи кругов Эйлера.

5.     Пересечение множеств.

6.     Объединение множеств.

7.     Законы пересечения и объединения множеств.

8.     Вычитание множеств. Дополнение одного множества до другого.

9.     Понятие разбиения множества на классы.

10. Некоторые задачи, связанные с операциями над конечными множествами.

11. Декартово произведение множеств.

12. Свойства операции декартова произведения.

13. Кортеж. Длина кортежа.

14. Понятие соответствия между  множествами.

15. Способы задания соответствий.

16. Соответствие обратное  данному. Взаимно однозначное соответствие.

17. Равномощные множества. Счетные множества.

 

Письменные задания

 

По теме: «Понятие множества»

1.       Назовите три элемента множества: а) учебных предметов, изучаемых в начальной школе; б) четных натуральных чисел; в) четырехугольников.

2.       В – множество четных чисел. Зная это, запишите с помощью символов следующие предложения: 1) число 20 четное; 2) число 17 не является четным.

3.       Запишите, используя символы: а) Число 14 – натуральное; б) Число – 7 не является натуральным; в) Число 0 – рациональное; г)  - число действительное.

4.       Даны числа: 325, 0, - 17, -3,8, 7. Установите, какие из них принадлежат множеству: 1) натуральных чисел; 2) целых чисел; 3) рациональных чисел; 4) действительных чисел.

5.       Прочитайте следующие высказывания и укажите среди них истинные:  1) 100 Î N; 2) –8 Î Z; 3) –8 Ï N; 4) 5,36 Î Q; 5) 102 Ï R;  6) ÎQ; 7) –7 Î R; 8)ÎN; 9) 0 Î Z.

6.       Р – множество натуральных чисел, больших 7 и меньше 14. Выясните, какие из чисел 13, 10, 5, 7, 14 ему принадлежат, а какие не принадлежат. Ответ запишите, используя знаки Î и Ï.

7.       А – множество решений уравнения х² + 1 = 0. Верно ли, что А – пустое множество? Приведите примеры уравнения, множество решений которого состоит из: а) одного элемента; б) двух элементов; в) трех элементов.

8.       Запишите с помощью знака равенства и фигурных скобок предложения: 1) Х – множество чисел 0, 1, 2, 3, 4, 5; 2) У - множество букв в слове «математика».

9.       Множество С состоит из квадрата, круга и треугольника. Принадлежит ли этому множеству диагональ квадрата?

10.   Перечислите элементы следующих множеств: А – множество нечетных однозначных чисел; В - множество натуральных чисел, не меньших 5; С – множество двузначных чисел, делящихся на 10.

11.   Укажите характеристическое свойство элементов множества: а) {а, е, е, и, о, у, э, ю, я, ы};  б) {23, 22, 21, 20, 19, 18, 17, 16, 15 };  в) {11, 22, 33, 44, 55, 66, 77, 88, 99}.

12.   Изобразите на координатной прямой  множество решений неравенства ( х- действительное число): 1) х > 5,3; 2) х  £ -3,8; 3) – 4,5£ х < 4; 4) 2,7 £ х £ 9.

13.   Найдите множество действительных корней уравнения: 1)3х=х+8;                         2) 3х+5=3(х+1); 3) 3(5х+10)=30+15х; 4)  х (х+16)=0.

14.   А - множество двузначных чисел, запись которых оканчивается цифрой 1. Принадлежит ли этому множеству числа 28, 31, 321, 61?

15.   Дано множество А = {5, 10, 15, 25}. Укажите два подмножества, равные множеству А.

16.   Известно, что элемент а содержится в множестве А  и в множестве В. Следует ли отсюда, что: 1) А Ì В; 2) В Ì А; 3) А = В?

17.   Известно, что каждый элемент множества А  содержится в  множестве В. Верно ли, что тогда: 1) А Ì В; 2) А = В?

18.   Из множества К = {216, 546, 153, 171, 234} выпишите числа, которые: 1) делятся на 3; 2) делятся на 9; 3) не делятся на 4; 4) не делятся на 5. Есть ли среди полученных подмножеств такое, которое равно множеству К?

19.   Установите, в каком отношении находятся множества решений неравенств и сами неравенства: 1) х < 12 и х < 10; 2) х < 12 и х > 15;  3) х < 12 и х>10; 4) х < 12 и –3х > -36.

20.   Изобразите при помощи кругов Эйлера отношения между множествами А и В, если: 1) А – множество четных чисел, В – множество чисел, кратных 3; 2) А - множество квадратов, B- множество прямоугольников; 3) А – множество квадратов, В – множество прямоугольных треугольников; 4) А – множество квадратов, B – множество прямоугольников с равными сторонами.

21.   Изобразите при помощи кругов Эйлера отношения между множествами А, В и С, если известно, что: 1) А Ì В и В Ì А; 2) А Ì В, С пересекается с В, но не пересекается с А; 3) А, В и С пересекаются, но ни одно не является подмножеством другого.

 

 

По теме: «Операции над множествами»

1.       Сформулируйте условия, при которых истинны следующие высказывания: 1) 5 Î А Ç В; 2) 7Î А Ç В.

2.       Известно, что х Î А. Следует ли из этого, что х Î А ÇВ?

3.       Известно, что х Î А ÇВ.  Следует ли из этого, что х Î А?

4.       Изобразите при помощи кругов Эйлера пересечение множеств А и В, если: 1) А Ì В; 2) В Ì А; 3) А Ç В = Æ.

5.       Найдите пересечение множеств А и В, если: 1) А = {a, b, c, d, e, f};  B = {b, e, f, k, l}; 2) А = {26, 39, 5, 58, 17, 81};  В = {17, 26, 58}; 3) А = {26, 39, 5, 58, 17, 81};  В = {2, 6, 3, 9, 1, 7}.

6.       М – множество однозначных чисел, Р – множество нечетных натуральных чисел. Из каких чисел состоит пересечение данных множеств? Содержатся ли в нем числа – 7 и 9?

7.       А – множество точек окружности, B – множество точек прямой а. Из скольких элементов может состоять пересечение данных множеств? Может ли оно быть пустым?

8.       Начертите два треугольника так, чтобы их пересечением: а) был треугольник; б) был отрезок; в) была точка.

9.       Используя координатную прямую, найдите пересечение множеств решений неравенств, в которых переменная  х – действительное число: 1) х >-2 и х > 0; 2) х >- 3,7 и  х £ 4; 3) х ³ 5 и х <- 7,5; 4) – 2< х< 4 и х ³ -1; 5) –7£х £ 5 и - 6 £ х £2.

10.   Начертите две фигуры, принадлежащие пересечению множеств С и D, если: а) С – множество ромбов, D – множество прямоугольников; б) С  - множество равнобедренных треугольников, D – множество прямоугольных треугольников.

11.   Сформулируйте условия, при которых истинны следующие высказывания: 1) 5ÎAÈB; 2) 7Î А È В.

12.   Известно, что х Î А. Следует ли из этого, что х Î А È В?

13.   Известно, что х Î А ÈВ.  Следует ли из этого, что х Î А?

14.   Изобразите при помощи кругов Эйлера объединение множеств А и В, если: 1) А Ì B;  2) B Ì A.

15.   Найдите объединение множеств А и В, если: 1) А = {a, b, c, d, e, f}; B = {b, e, f, k, l}; 2) А = {26,39,5,58,17,81}; B = {17,26,58}; 3) А = {26,39,5,58,17,81}; B = {2,6,3,9,1,7}. 

16.   М – множество однозначных чисел, Р – множество нечетных натуральных чисел. Из каких чисел состоит объединение данных множеств? Содержатся ли в нем числа – 7 и 9?

17.   Используя координатную прямую, найдите объединение множеств решений неравенств, в которых переменная  х – действительное число: 1) х >-2 и х > 0; 2) х > - 3,7 и  х  £ 4; 3) х ³ 5 и х < - 7,5; 4) – 2 < х < 4 и х ³ - 1; 5) – 7 £ х £ 5 и - 6 £ х £ 2.

18.   Известно, что х Î А ÇВ. Следует ли из этого, что  а) х Î В Ç А; б) х Î А È В;   в) х Î В È А ?

19.   Принадлежит  ли  элемент  х  объединению  множеств A,  B  и  С, если: 1) хÎA; 2)  х ÎА  и  х ÎB; 3) х ÎА, х ÎВ  и  х ÎС;  4) х ÏA,  но  х ÎС; 5) х ÏA,  но  х ÎС   и  х ÎB?

20.   Определите порядок выполнения действий в следующих выражениях: а)  А È В È С; б) А  Ç В  È С Ç D; в) А Ç В Ç С; г) А  È В  Ç С È D.

21.   Постройте три круга, представляющие попарно пересекающиеся множества А, В и С, и отметьте штриховкой области, изображающие множества: а) А Ç В Ç С; б) (А  Ç В)  È С; в) А  Ç В  È С; г) А È В È С; д) (А  È В)  Ç С; е) (А  È С) Ç (В  È С). Для каждого случая сделайте отдельный рисунок.

22.   Х – множество двузначных чисел, Y - множество четных  чисел, Р- множество чисел, кратных 4. Каковы характеристические свойства элементов множеств А = C ÇUÇR и B = (CÈU)ÇR?  Изобразите множества C, U, R, А и В при помощи кругов Эйлера. Назовите три числа, принадлежащие множеству А, и три числа, принадлежащие множеству В.

23.   А – множество ромбов, В – множество треугольников, С – множество многоугольников, содержащих угол 60°. Начертите две фигуры, принадлежащие множеству Х = AÇСÈBÇС.

24.      Проиллюстрируйте, используя круги Эйлера, следующие свойства: а) ассоциативности пересечения множеств; б) дистрибутивности пересечения относительно объединения множеств; в) дистрибутивности объединения относительно пересечения множеств.

25.   Среди следующих выражений найдите такие, которые представляют собой равные множества: а) Р Ç М Ç К; б) Р  Ç (М  È К); в) Р  Ç  М È Р Ç К; г) (Р  È М) È К; д) Р  È (М  Ç К); е) (М  È Р ) Ç (Р  È К).

26.   Найдите разность множеств А и В, если: а)  А =   {1, 2, 3, 4, 5, 6}, В =   { 2, 4, 6, 8, 10}; б) А =   {1, 2, 3, 4, 5, 6}, В = Æ; в) А =   {1, 2, 3, 4, 5, 6}, А =  {1, 2, 3, 4, 5, 6}; г) А =   {1, 2, 3, 4, 5, 6}, В =  {6, 2, 3, 4, 5, 1}.

27.   В какие случаях, выполняя предыдущее упражнение, вы находите дополнение множества В до множества А?

28.   Найдите дополнение множества С до множества D, если: 1) С = {а, б, в, г, д, е}; D  = {а, б, в, г, д, е, ж, и}; 2)  С = {41, 42}; D  = {40, 41, 42, 43, 44}; 3). С = {9, 10, 11, 12}; D  = {11, 9, 12, 10}.

29.   Даны множества: А – натуральных чисел, кратных 3, В – натуральных чисел, кратных 9. а) Сформулируйте характеристическое свойство элементов множества В’_А ;  б) Верно ли, что 123 Î В’_А, а 333 Ï В’_А ?

30.   Проиллюстрируйте при помощи кругов Эйлера, что для любых множеств А, В и С верны равенства: а) А \ (В È С) = (А \ В) Ç (А \ С); б) А \ (В Ç С) = (А \ В) È (А \ С); в) (А È В) \ С= (А \ С) È (В \ С); г) (А \ В) Ç С = (А Ç С) \ (В Ç С).

31.   Х – множество равнобедренных треугольников, У – множество равносторонних треугольников. Начертите два треугольника, принадлежащие множеству Х \ У.

32.   Из каких чисел состоит дополнение: 1) множества натуральных до множества целых; 2) множества целых чисел до множества рациональных; 3) множества рациональных чисел до множества действительных?

 

 

По теме: «Разбиение множества на классы»

1.       Выделите из множества К={0, 2, 6, 8, 9, 12, 15} два подмножества. В одно включите числа, кратные 2, а в другое – кратные 3. Произошло ли разбиение множества К на класс чисел, кратных 2, и класс чисел, кратных 3?  Можно ли разбить данное множество К на три класса: К₁=  {0,2,6},  К₂=  {8,9}, К₃=  {12,15}?

2.       Определите классы  разбиения множества Х четырехугольников, если оно осуществляется при помощи: 1) свойства «быть прямоугольником»; 2) свойств «быть прямоугольником» и «быть ромбом»; 3) свойств «быть прямоугольником» и «быть квадратом»; 4) свойств «быть прямоугольником» и «быть трапецией».

3.       Из множества натуральных чисел выделите подмножество чисел, кратных 8. На сколько классов при этом произошло разбиение множества натуральных чисел? Изобразите полученные классы при помощи кругов Эйлера и назовите по два представителя из каждого класса.

4.       На какие классы разбивается множество точек плоскости при помощи: а) окружности; б) круга; в) прямой?

5.       На множестве натуральных чисел рассматривается свойство «быть кратным 7». Сколько классов разбиения множества N оно определяет? Назовите по два элемента из каждого класса.

6.       Из множества четырехугольников выделили подмножество фигур с попарно параллельными сторонами. На какие классы разбивается множество четырехугольников с помощью свойства «иметь попарно параллельные стороны»? Начертите по два четырехугольника из каждого класса.

7.       Изобразите при помощи кругов Эйлера множество N натуральных чисел и его подмножества: четных чисел и чисел кратных 7. Можно ли утверждать, что множество N разбито: а) на два класса: четных чисел и чисел, кратных 7;  б) на четыре класса: четных чисел, кратных 7; в) нечетных чисел, не кратных 7; г) четных чисел не кратных 7; д) нечетных чисел, кратных 7.

8.       На множестве четырехугольников рассматриваются два свойства: «быть прямоугольником» и «быть квадратом». На какие классы разобьется множество четырехугольников при помощи этих свойств? Начертите по два четырехугольника из каждого класса.

9.       Изменится ли ответ в предыдущем упражнении, если на множестве четырехугольников рассмотреть свойства: а) «быть прямоугольником» и «быть ромбом»; б) «быть прямоугольником» и «быть трапецией»?

10.   Можно ли узнать, сколько человек в классе, если в нем: 1) 17 мальчиков и 15 девочек; 2) 17 мальчиков и 23 спортсмена?

11.   Из 50 учащихся 37 изучают английский язык, 17- немецкий. Сколько человек изучают оба языка?

 

 

По теме: «Декартово произведение»

 

1.                     Элементами множеств А и В являются пары чисел:  А = {(1,12), (2, 9), (3,6), (4, 3), (5, 0)}, В = {(1,9), (2,7),(3,6), (4,7), (5,0)}. Найдите пересечение и объединение данных множеств.

2.                     Запишите различные двузначные числа, используя цифры 3, 4 и 5. Сколько среди них таких, запись которых начинается с цифры 3? Как связано решение данной задачи с понятием декартова произведения множеств?

3.                     Перечислите элементы декартова произведения A ´ В, если: а) А = {a,b,c, d}, B = { b, k, l}; б) А = В = {a, b, c}; в) А = {a, b, c}, В = Æ.

4.                     Даны множества А = {1, 3, 5} и  В = {2, 4}. Перечислите элементы множеств A ´ В и В ´ А. Верно ли, что: а) Множества A ´ В и В ´ А содержат одинаковое число элементов; б) Множества A ´ В и В ´ А равны?

5.                     Проверьте справедливость равенства (AÈB) ´ С = (A ´ С) È (B ´ С) для множеств А = {3, 5, 7}, В = {7, 9}, С = {0, 1}. Выполняется ли для них равенство (A \ B) ´ С = (A ´ С) \ (B ´ С) ?

6.                     Сколько букв в слове «барабан»? Сколько различных букв в этом слове? Сформулируйте эту задачу, используя понятия множества и кортежа.

7.                     Чем отличается множество цифр в записи числа 56576 от кортежа цифр в его записи?

8.                     Изобразите в прямоугольной системе координат множество A ´ В, если: а) А = [-2; 2]. В = {2, 3, 4}; б) А = [-2; 2]. В = (2, 4);  в) А = R, В = [2; 4].

 

 

По теме: «Соответствия между двумя множествами»

 

1.       Вычислив длины заданных отрезков, учащийся записал: АВ = 7см, СD = 12 см, KL  = 15cм,  XY= 12см. Соответствие между какими множествами он установил? Задайте это соответствие при помощи предложения с двумя переменными и графа.

2.       Даны множества: Х = {2,5}, Y = {3,6}. Перечислите элементы декартова произведения данных множеств и образуйте все подмножества полученного множества. Какое из подмножеств задает соответствие: а) «больше»; б) «меньше»; в) «меньше на 1»; г) «меньше в 3 раза»?

3.       Соответствие «число х в два раза больше числа у» рассматривается между множествами Х и Y . Каким будет его график, если: а) Х = {2,4,6,8}, Y  = N;  б) Х = [2,8], Y  = R;  в) Х = Y  = R.

4.       Множества Х = {1,3,4,6} и Y = {0,1} находятся в соответствии S = {(1,1), (3,0), (3,1), (4,0), (4,1), (6,1)}. Задайте соответствие S^-1, обратное соответствию S, и постройте на одном чертеже их графики.

5.       Между множествам Х – углов треугольника АВС и множеством Y  – его сторон задано соответствие Т – «угол х лежит против стороны у». Задайте соответствие  Т^-1, обратное соответствию Т, при помощи: а) предложения с двумя переменными; б) графа.

6.       Задайте при помощи графа соответствия между множествами Х = {а, б, с} и Y  = {2, 4, 6} так, чтобы одно из них было взаимно однозначным.

7.       Даны множества: А= {1,2,5}, В = {3,7}. Найдите А´B и В´А. Верно ли, что найденные множества равномощны?

8.       Докажите, что множество А счетно, если: а) А = {9, 10, 11, 12,…}; б) А = {а êа = 3п, п ÎN}; в) А = {а êа = п², п ÎN}.

10.   Покажите, что выполняя нижеприведенные задания, учащиеся начальных классов используют понятие равночисленности множеств: а) У Димы было 28 марок, а у Коли на 7 марок больше. Сколько марок было у Коли? б) У Маши 9 игрушек, а у Риты на 2 меньше. Сколько игрушек у Риты? в) Для детского сада купили 4 зеленых мяча, а красных в 3 раза больше, чем зеленых. Сколько красных мячей купили детям? г) Для детского сада купили 15 красных мячей, а зеленых в 3 раза меньше. Сколько зеленых мячей купили детям? д) Нарисуй на другой фигуре столько же точек, сколько на первой (точки не пересчитывать).

е) Нарисуй, не считая, столько же квадратов и столько же отрезков, сколько на рисунке треугольников.

 

 

 

 

 

КОНТРОЛЬНАЯ (ЗАЧЕТНАЯ) РАБОТА

Группа А

1. Выбери правильный из ответов:

а) множество – это набор объектов определенной природы;

б) под множеством понимают совокупность объектов, отвечающих определенным свойствам;

в) под множеством понимают совокупность элементов, которые можно пересчитать.

2. Среди следующих высказываний укажите истинные: а) 100 Î N; б) -8 Î Z; в) 5,36 Î Q; г)  Î N;  д) 0 Î Z; е) -3ÏN; ж) Î Q; з)102ÏR;  и) 1,3Î N.

3.  Х – множество прямых плоскости. Какое из следующих отношений является отношением эквивалентности на этом множестве: а) «х параллельна у»; б) «х перпендикулярна у»; в) «х пересекает у»? 

Группа Б

1. Найдите АÈB, АÇB, А \ В, если: А = { х | хÎR, -5< х< 5}, В = { х | хÎR, 1£  х < 4}.

2.       Из множества К = {0, 2, 6, 8, 9, 12, 15}выделили два подмножества:  К₁  - числа, кратные 2; К₂  -числа, кратные 3. Произошло ли разбиение множества К на классы? Почему?

3. На множестве Х={0, 3, 6, 9, 12, 15, 18} задано отношение R. Перечислите пары чисел, связанных этим отношением и постройте его граф, если: а) R – « х больше у в 3 раза»; б) R – « х больше у на 3».

Группа В

1.          Даны два множества А ={4, 6, 8} и В ={3, 7}. Найдите множества А ´B и B´A. Можно ли установить взаимно однозначное соответствие между ними?

2. Проверьте справедливость равенства (A \ B)´С=(A´С) \ (B´С) для множеств А = {3, 5, 7}, В = {5, 7}, С   = {1, 4}.

3. На множестве Х = { 12, 13, 14, 15, 16, 17, 18, 19, 20, 21} задано отношение «иметь один и тот же остаток от деления на 4». Показать, что данное отношение есть отношение эквивалентности, записать все классы эквивалентности, на которые разбивается множество Х, построить граф этого отношения.

 

Критерии оценки: Задания группы А оцениваются 1 баллом, группы Б – 2 баллами, группы В – 3 баллами. Выполнение заданий группы А обязательно; за каждое не правильно выполненное задание этой группы от общего количества баллов вычитают 1 балл. За 7-10 баллов студент получает оценку «3» (зачет), за 11-14 – оценку «4», за 15 – 18 – оценку «5».

 

Тема 1.2. Текстовая задача

Вопросы к изучению

1.       Роль и место задач в начальном курсе математики. Функции текстовых задач

2.       Структура процесса решения задач

3.       Методы и способы решения текстовых задач

4.       Этапы решения и приемы их выполнения

5.       Решение типовых задач: “задач на части”, “на движение”(С/Р)

 

Письменные задания:

1.       Решите различными способами (практическим, арифметическим, алгебраическим, графическим) следующую задачу: «В гараже стояло 10 машин. После того, как несколько машин уехало, осталось 6. Сколько машин выехало из гаража?».

2.       С противоположных концов катка длиной 180 м бегут навстречу друг другу два мальчика. Через сколько секунд они встретятся, если начнут бег одновременно и если один пробегает 9 м в секунду, а другой 6 м в секунду?

Объясните, используя условия данной задачи, смысл следующих выражений: а) 9+6; б)180:9; в) 180:6; г) 180:(9+6). Какое из этих выражений является решающей моделью данной задачи?

3.       Запишите решение задачи в виде выражения:

а) Самолет пролетел за 2 ч а км. Сколько километров он пролетит за 5 ч?

б) Из двух городов, расстояние между которыми 9 км, одновременно навстречу друг другу выехали легковой автомобиль и грузовой и встретились через t ч. Скорость легкового автомобиля v км/ч. Найдите скорость грузовика.

в) Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля v₁ км/ч, а скорость мотоцикла v₂ км/ч.

4.       Два пассажира метро, начавшие одновременно один спуск, другой подъем на движущихся лестницах метро, поравнялись через 30 с. Вычислите длину лестницы, если скорость ее движения 1 м/с.Решите задачу двумя арифметическими способами.

5.       Расстояние между городами А и В 520 км. В 8 ч из А в В выехал автобус со скоростью 56 км/ч, а в 11 ч того же дня из В в А выехал грузовой автомобиль со скоростью 32 км/ч. На каком расстоянии от А встретятся машины? Решение задачи запишите по действиям и в виде выражения.

6.       Из двух городов, расстояние между которыми 960 км, вышли одновременно навстречу друг другу два поезда и встретились через 8 ч после выхода. Найдите скорость каждого поезда, если один проходил в час на 16 км больше другого.

7.       Решите нижеприведенные задачи арифметическим методом; решение запишите по действиям с пояснениями.

а) Из А в В выехал мотоциклист, проезжавший в час 48 км. Через 45 мин из В в А выехал другой мотоциклист, скорость которого была 50 км/ч. Зная, что расстояние АВ равно 330 км, найдите, на каком расстоянии от В мотоциклисты встретятся.

б) Из двух городов, расстояние между которыми 484 км, выехали одновременно навстречу друг другу велосипедист и мотоциклист. Через 4 ч расстояние между ними оказалось 292 км. Определите скорость велосипедиста и мотоциклиста, если скорость мотоциклиста в 3 раза больше скорости велосипедиста.

8.       Установите, достаточно ли данных для ответа на требование задачи:

а) Из двух сел, расстояние между которыми 36 км, вышли одновременно навстречу друг другу два пешехода и встретились. Скорость одного пешехода 4 км/ч. С какой скоростью шел другой пешеход?

б) Расстояние между станциями 780 км. Одновременно навстречу друг другу с этих станций вышли два поезда и через 6 ч встретились. Найдите скорость каждого поезда, если скорость одного из них на 10 км/ч больше скорости другого.

В случае если нельзя ответить на требование задачи, дополните ее условие недостающими данными и решите задачу.

9.       Есть ли среди нижеприведенных задачи с лишними данными:

а) Расстояние между плотом и катером, которые движутся по р навстречу друг другу, 52 км. Скорость плота 4 км/ч, а скорость кат 9 км/ч. Как изменится расстояние между ними через час?

б) Почтальон живет на расстоянии 24 км от почтового отделен Путь от дома до почты он проехал за 3 ч на велосипеде со скоростью 8 км/ч, а обратный путь по той же дороге он проехал со скоростью 6 км/ч. На какой путь почтальон потратил меньше времени и на сколько часов?

В случае если в задаче есть лишние данные, то исключите их и запишите получившуюся задачу.

10.   Два теплохода отправились одновременно от пристани в одном и том же направлении. Скорость одного теплохода 25 км/ч, другого 20 км/ч. Первый пришел к конечной остановке на 4 ч раньше, чем второй. Найдите расстояние между пристанью и конечной остановкой.

Постройте вспомогательную модель задачи, используя таблицу. Объясните, используя условие данной задачи, смысл следующих выражений: а) 20 × 4; б)25-20; в) (20 × 4): (25-20). Есть ли среди этих выражений решающая модель задачи? Запишите решение задачи в виде выражения и найдите его значение. Выполните проверку, решив задачу алгебраическим методом.

11.   Решите следующие задачи арифметическим методом; решение запишите по действиям и выполните проверку:

а) Из двух городов, расстояние между которыми 260 км, одновременно выехали два поезда в одном направлении. Скорость шедшего впереди поезда 50 км/ч, а второго - 70 км/ч. Через какое время один поезд догонит другой?

б) Из пункта А выехал автобус со скоростью 40 км/ч и через 12 мин нагнал пешехода, который вышел из пункта В одновременно с началом движения автобуса из пункта А. Скорость пешехода 5 км/ч. Какое  расстояние между пунктами А и В?

в) Скорость одного конькобежца на 2 м/с больше скорости другого. Если второй начнет движение на 20 с раньше первого, то первый стартуя с того же места, что и второй, догонит его через 80 с. Определите скорости спортсменов.

12.   Два самолета вылетели одновременно из одного города  в два различных пункта. Кто из них долетит до места назначения быстрее, если первому из них нужно пролететь вдвое большее расстояние, но зато он летит в два раза быстрее, чем второй?

13.   От двух пристаней, расстояние между которыми по реке 640 км, вышли одновременно навстречу друг другу два теплохода. Собственная скорость теплоходов одинакова. Скорость течения реки 2 км/ч. Теплоход, идущий по течению, за 9 ч проходит 198 км. Через сколько часов теплоходы встретятся?

14.   Есть ли среди следующих задач задачи с недостающими или избыточными данными:

а) Турист проехал поездом и на лошади 288 км, причем на лошади он проехал 48 км. Поездом он ехал 4 ч, а на лошади - 3 ч. С какой скоростью ехал турист на лошади, если скорость поезда 60 км/ч?

б) Турист проехал поездом и на лошади 288 км. Поездом он ехал 4 ч на лошади - 3 ч. С какой скоростью ехал турист на лошади?

в) Турист проехал поездом и на лошади 288 км. Поездом он ехал 4 а на лошади - 3 ч. С какой скоростью ехал турист на лошади, если поезд шел со скоростью 60 км/ч?

Творческие задания

1.       Решите следующие задачи арифметическим методом; решение запишите по действиям с пояснением:

а) На путь по течению реки моторная лодка затратила 6 ч, а на об­ратный путь - 10 ч. Скорость лодки в стоячей воде 16 км/ч. Какова скорость течения реки?

б) Собственная скорость моторной лодки в 8 раз больше скорости течения реки. Найдите собственную скорость лодки и скорость тече­ния реки, если, двигаясь по течению, лодка за 4 ч проплыла 108 км.

в) На школьных соревнованиях по плаванию один ученик проплыл некоторое расстояние по течению реки за 24 с и то же расстояние против течения за 40 с. Определите собственную скорость пловца, считая ее постоянной от начала и до конца заплыва, если скорость течения реки равна 0,25 м/с.

2.       Решите задачи арифметическим методом, установив предварительно, о каких процессах в них идет речь, какие величины рассматриваются и в каких зависимостях они находятся:

а) Длина прямоугольного поля 1536 м, а ширина 625 м. Один тракторист может вспахать это поле за 16 дней, а другой за 12 дней. Какую площадь вспашут оба тракториста, работая вместе в течение 5 дней?

б) В мастерской было два куска ткани: один длиной 104 м, другой -84 м. Из всей ткани сшили одинаковые платья, причем из первого куска получилось на 5 платьев больше, чем из второго. Сколько всего платьев сшили из этой ткани ?

в) Один экскаватор вынимает на 60 м³ в час больше земли, чем дру­гой. Оба экскаватора вынули вместе 10320 м³ земли, причем первый работал 20 ч, а второй - 18 ч. С какой производительностью работал каждый экскаватор?

г) Два человека чистили картофель. Один очищал в минуту 2 картофелины, а второй - 3 картофелины. Вместе они очистили 400 штук. Сколько времени работал каждый, если второй проработал на 25 мин больше первого?

д) Бассейн вмещает 2700 м³ воды и наполняется тремя трубами. Первая и вторая трубы вместе могут наполнить бассейн за 12 ч, а первая и третья наполняют его вместе за 15ч. За сколько часов каждая труба в отдельности наполняет бассейн, если третья труба действует вдвое медленнее второй?

 

 

 

 

 

«Обоснование выбора действий при решении текстовых задач в начальной школе»

 

Теоретическая часть

Вопросы к изучению

1.       Смысл натурального числа, полученного в результате измерения величины.

2.       Смысл суммы, разности, произведения и частного таких чисел.

3.       Обоснование  выбора действий при решении текстовых задач в начальной школе.

 

 

Практическая часть

1.       Какой смысл имеет натуральное число 7, если оно получено в результате измерения: а) длины отрезка; б) площади фигуры; в) массы тела?

2.       Верно ли, что при увеличении единичного отрезка в k раз соответствующие численные значения длин отрезка уменьшаются во столько же раз?

3.       Объясните, почему следующие задачи решаются при помощи сложения:

     а) Когда из ящика взяли 4 кг яблок, то в нем осталось 6 кг. Сколь­ко килограммов яблок было в ящике первоначально?

     б) На пошив кофты израсходовали 2 м ткани, а на платье на 3 м больше. Сколько метров ткани израсходовали на платье?

4.       Объясните, почему следующие задачи решаются при помощи   вычитания:

 а) От ленты длиной 5 м отрезали 2 м. Сколько метров ленты осталось?

 б) С первого участка собрали 10 мешков картофеля, а со второго на 3 мешка меньше.    Сколько мешков картофеля собрали со второго участка?

5.       Обоснуйте выбор действий при решении следующих задач:

а) Мама купила 5 кг огурцов, 2 кг свеклы и помидоры. Сколько килограммов помидоров купила мама, если масса всех овощей 12 кг?

б) На одной полке 30 книг, на другой на 7 книг меньше. Сколько книг на двух полках?

в) От проволоки длиной 15 дм отрезали сначала 2 дм, а потом еще 4дм.  Сколько   дециметров проволоки осталось?

г) За лето первоклассники собрали 8 кг лекарственных трав, второклассники на 4 кг больше первоклассников, а третьеклассники на 3кг меньше второклассников. Сколько килограммов лекарственных  трав собрали третьеклассники?

6.       Объясните различными способами, почему следующие задачи решаются при помощи умножения:

а) В одной корзине 5 кг яблок. Сколько килограммов яблок в трех таких корзинах?

б) За один день Саша прочитывает 4 страницы книги. Сколько страниц в книге, если Саша прочитал ее за 6 дней.

7.       Объясните различными способами, почему следующие задачи решаются при помощи деления:

а) 8 кг варенья надо разложить в банки по 2 кг в каждую. Сколько получится банок?

б) На садовом участке посадили 15 кустов смородины по 5 кустов в каждом ряду. Сколько было рядов?

8.          Обоснуйте выбор действий при решении следующих задач:

а) С трех овец настригли 18 кг шерсти. Сколько шерсти можно получить с 5 таких овец?

б) В пятиэтажном доме 80 квартир. На каждом этаже в подъезде и 4 квартиры. Сколько подъездов в этом доме?                    

Творческие задания

Решите задачи и выполните проверку решения. Какие величины рассматривались в задачах?

1.          Экспедиция высадилась на Северном полюсе 21 мая 1937 года. Какого числа закончилась работа станции “Северный полюс-1”, если исторический дрейф продолжался 8 месяцев и 29 дней?

2.          Первое кругосветное путешествие закончилось 6 сентября 1522 года и продолжалось 2 года 11 месяцев 17 дней. Определите дату отплытия Магеллана из Сен-Лукара (морской порт Севильи).

3.          Старейшие российские университеты - Московский и Ленинградский были основаны 11 января 1755 года и 8 февраля 1819 года. Сколько времени прошло между основаниями Московского и Ленинградского университетов? Сколько времени существует каждый из этих университетов?

4.          В хозяйстве под гречиху и овес отвели 700 га, причем площадь, отведенная под овес, была на 60 га больше площади, отведенной под гречиху. Сколько гектаров было отведено под овес и сколько под гречиху?

5.          Прямоугольный участок с периметром 900 м и отношением длин сторон 1:8 занят под чайную плантацию. С 1 га снимали 50 кг чайного листа. Выход готового чая составляет четвертую часть массы чайного листа. Сколько 50-граммовых пачек чая и на какую сумму получится с чайного листа, собранного с этого участка, если пачка чая стоит 40 коп.?

6.          Из 6 кг свекловицы получается 600 г сахара рафинада. Сколько сахара получится из 500 кг свекловицы?

7.          Делая в среднем по 42 км/час., поезд прошел расстояние между городами за 30 часов. С какой скоростью должен идти поезд, чтобы пройти это же расстояние за 24 часа?

8.          За 125 кВт/час. электроэнергии уплатили 25 грн. Сколько надо уплатить за 75 кВт/час. электроэнергии?

9.          36 рабочих закончили работу за 20 дней, работая по 8 часов в день. За сколько дней 40 рабочих выполнят ту же работу, работая по 6 часов в день?

 

 

Тема1.3. «Методы математической статистики»

Вопросы к изучению:

1.     Роль комбинаторных задач в курсе начальной математики.

2.     Правила суммы и произведения.

3.     Размещения и сочетания.

 

Письменные задания:

1.                     Сколько существует двузначных чисел, которые записываются различными цифрами?

2.                     Сколькими способами из отряда в 20 человек можно выбрать командира и знаменосца?

3.                     Сколькими различными способами можно построить в шеренгу 5 человек?

4.                     Сколько различных двузначных чисел можно записать, используя цифры 3,4, 5 и 6? Сколько различных двузначных чисел можно записать, используя при записи числа каждую из указанных цифр только один раз? Запишите эти числа.

5.                     Сколько трехзначных чисел можно составить из трех различных, не равных нулю цифр? Зависит ли результат от того, какие цифры взяты? Укажите какой-нибудь способ перебора трехзначных чисел, при котором ни одно число не может быть пропущено.

6.                     Сколько всевозможных трехзначных чисел можно составить из цифр 1,2,3 и 4 так, чтобы цифры в записи числа не повторялись? Изменится ли решение этой задачи, если вместо цифры 4 будет дана цифра 0?

7.                     Сколько всевозможных четырехзначных чисел можно составить, используя для записи цифры 1,2.3 и 4? Какова разность между самым большим и самым маленьким из них?

8.                     Покажите, что в нижеприведенных задачах рассматриваются размещения из k элементов по m; определите значения k  и m и найдите число размещений: а) Из 20 учащихся класса надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать? б) В классе изучаются 7 предметов. В среду 4 урока, причем все разные. Сколькими способами можно составить расписание на среду? в) В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места? г) Сколько всевозможных трехзначных чисел можно записать, ис­пользуя цифры 3, 4, 5 и 6?

9.                     Покажите, что в следующих задачах рассматриваются сочетания из k элементов по m, определите значения k и m и найдите число для каждой задачи: а) Сколькими способами можно выбрать из 6 человек комиссию, состоящую из трех человек? б) Сколькими способами можно выбрать 4 краски из 10 различных красок?

10.                 Два человека обменялись своими фотокарточками. Сколько бы­ло всего фотокарточек?

11.                 Два человека пожали друг другу руки. Сколько было рукопожатий? А если 15 человек пожали друг другу руки, то сколько будет рукопожатий?

12.                 Сколькими способами можно расставить на полке 3 различные книги? Переставить три различные буквы, три различные цифры?

13.                 15 человек сыграли друг с другом по одной партии в шахматы. Сколько было сыграно партий?

14.                 На плоскости отметили 7 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?

15.                 Решите следующие задачи, используя формулы. Ответ проверьте с помощью перебора всех возможных вариантов:

а) Сколько словарей необходимо переводчику, чтобы он мог пе­реводить непосредственно с любого из четырех языков - русского, английского, немецкого и французского - на любой другой из этих языков?

б) Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько различных вариантов флагов с белой, синей и красной полосами можно составить?

в) Мальчик выбрал в библиотеке 5 книг. По правилам библиотеки одновременно можно взять только 2 книги. Сколько у мальчика вариантов выбора двух книг из пяти?

г) Четыре друга собрались на футбольный матч. Но им удалось купить только три билета. Из скольких вариантов им надо выбрать тройку счастливцев? Как осуществить выбор, чтобы у всех ребят равные шансы попасть на матч?

д) В классе три человека хорошо поют, двое других играют на  гитаре, а еще один умеет показывать фокусы. Сколькими способами можно составить концертную бригаду из певца, гитариста и фокусника?

е) Задача Леонарда Эйлера. Трое господ при входе в ресторан дали швейцару свои шляпы, а при выходе получили их обратно. Сколько существует вариантов, при которых каждый из них получит чужую шляпу?

ж) Имеется ткань двух цветов: голубая и зеленая, и требуется обить диван, кресло и стул. Сколько существует различных вариантов обивки этой мебели?

16.                 Ниже приведены комбинаторные задачи для учащихся начальных классов. Решите их методом перебора и используя формулы комбинаторики. Выбор формул обоснуйте.

а) Аня, Боря, Вера и Гена - лучшие лыжники школы. На соревнования надо выбрать из них троих. Сколькими способами можно это сделать?

б) Круг разделили на две части и решили раскрасить их карандашами разных цветов. Сколькими способами можно это сделать, имеются красный, зеленый и синий карандаши?

в) При изготовлении авторучки корпус и колпачок могут иметь одинаковый или разный цвет. На фабрике есть пластмасса четырех цветов: белого, красного, синего и зеленого. Какие отличающиеся по цвету ручки можно изготовить?

г) На прямой взяли 4 точки. Сколько всего получилось отрезков, концами которых являются эти точки?

д) За свои рисунки ученик получил две положительные отметки. Какими они могут быть?

е) В соревнованиях участвуют 5 футбольных команд. Каждая команда играет один раз с каждой из остальных команд. Сколько матчей будет сыграно?

 

ВОПРОСЫ ДЛЯ КОЛЛОКВИУМА

1.       Математические понятия. Объем и содержание понятия.

2.       Отношения рода и вида между понятиями.

3.       Определение понятий.

4.       Требования к определению понятий.

5.       Контекстуальные и остенсивные определения.

6.       Высказывания  и высказывательные формы.

7.       Конъюнкция и дизъюнкция высказываний.

8.       Конъюнкция и дизъюнкция высказывательных форм.

9.       Высказывания с кванторами.

10.   Истинность высказываний с кванторами.

11.   Отрицание высказываний и высказывательных форм.

12.   Отношения следования между предложениями.

13.   Отношения равносильности между предложениями.

14.   Структура теоремы.

15.   Отличие теоремы от правила.

16.   Виды теорем.

17.   Роль и место задач в начальном курсе математики. Функции текстовых задач.

18.   Структура процесса решения задач.

19.   Методы и способы решения текстовых задач.

20.   Этапы решения и приемы их выполнения.

21.   Решение типовых задач: «задач на части», «на движение».

22.    Роль комбинаторных задач в курсе начальной математики.

23.    Правила суммы и произведения.

24.    Размещения и сочетания.

 

 

 

 

 

 

 

 

 

 

 

Раздел2.  «Натуральные числа и нуль»

 

Тема 2.1. «Понятие натурального числа»

 

 «История возникновения понятия натурального числа»

Вопросы к изучению

1.     Содержание понятий «множество», «число», «цифра», «счет».

2.     Развитие понятий числа и счета.

3.     Раскрытие сущности счета и измерения.

4.     Виды письменной нумерации и история их развития.

5.     Порядковые и количественные натуральные числа. Счет.

6.     Теоретико-множественный смысл количественного натурального числа и нуля

Вопросы для самоконтроля

1.     Назовите виды множеств, дайте им характеристику. Какие можно производить операции  над множествами?

2.     Что такое «число», «цифра», «счет»?

3.     В чем связь и различие счета и измерения?

4.     Раскройте причины возникновения различных видов записи чисел, дайте им характеристику.

5.     Какое значение имело возникновение понятия натурального числа на развитие математики?  

6.     Раскройте порядковый и количественный смысл натурального числа.

7.     Дайте теоретико-множественную трактовку натурального числа.

Задания для самостоятельной работы

1.       Подготовить короткое сообщение по истории возникновения письменной нумерации  и возникновения понятия натурального числа.

2.       рассматривается Рассмотрите материал учебников математики для начальной школы, где дочисловой период. Приведите примеры различных заданий по формированию у младших школьников счетной деятельности.

3.       Можно ли назвать отрезком натурального ряда множество: а){1,2,3,4}; б){2,3,4, 5}; в){1,3,5,7}; г){1,2,4,5}?

4.     Докажите, что множество В конечное, если: а) В - множество букв в слове «параллелограмм»; б) В - множество учащихся в классе; в) В - множество букв в учебнике математики.

5.       Прочитайте записи: n (А) = 5; n (А) = 7. Приведите примеры множеств, содержащих указанное число элементов.

6.     Что значит сосчитать элементы конечного множества? Сформулируйте правила, которые должны соблюдать учащиеся при счете предметов и которые вытекают из определения счета элементов конечного множества.

7.     Рассмотрите иллюстрации и записи, приведенные на той странице учебника по математике, где учащиеся изучают число «три». Объясните, какие из них приведены с целью раскрыть учащимся порядковое и количественное значение числа «три». Какие бы Вы добавили иллюстрации с этой же целью ?

8.       Найдите в различных учебниках математики для 1 класса задания, которые можно использовать для формирования у учащихся представлений: а) о количественном и порядковом числе; в) о взаимосвязи между количественным и порядковым числами. Ответьте на вопрос: «Почему установление взаимно однозначного соответствия между элементами предметных множеств подготавливает ребенка к овладению счетом?».

9.       Найдите в учебниках различные виды учебных заданий, которые можно предложить детям для усвоения отношений «больше», «меньше», «равно» между однозначными числами. Составьте сами различные задания, которые можно использовать с этой же целью.

10.                 Составьте учебные задания, в процессе выполнения которых у учащихся формируются навыки присчитывания и отсчитывания по единице.

 

 

 «Теоретико-множественный смысл суммы, разности, произведения, частного и отношения «меньше»

 

Вопросы к изучению

1.       Теоретико-множественный смысл натурального числа, нуля и отношения «меньше»

2.       Теоретико-множественный смысл суммы

3.       Теоретико-множественный смысл разности

4.       Теоретико–множественный смысл произведения

5.       Теоретико– множественный смысл частного

 

Письменные задания:

1.       Почему на уроке, где изучается число «четыре», можно исполь­зовать картинку с изображением четырех яблок, четырех тетрадей, а можно воспользоваться и другими примерами четырехэлементных множеств?

2.       Какой подход к определению отношения «меньше» используется при ознакомлении младших школьников с неравенством 3 < 4, если выполняются следующие действия: возьмем три розовых кружка и четыре синих и каждый розовый кружок наложим на синий; видим, что синий кружок остался незакрытым, значит, розовых кружков меньше, чем синих, поэтому можно записать: 3 < 4.

3.       Исходя из различных определений отношения «меньше», объяс­ните, почему 2 < 5?

4.       Как, используя теоретико-множественный подход к числу, объ­яснить, что 4 = 4?

5.       Каков теоретико-множественный смысл суммы: а) 3+5; б) 0+4; в) 0+0.

6.       Дайте теоретико-множественное истолкование суммы k слагаемых и, используя полученный вывод, объясните теоретико-множественный смысл суммы: а) 3 + 4 + 2; б) 1 + 2 + 3 + 4.

7.       Объясните, почему нижеприведенные задачи решаются сложением.

а) Дима сорвал 8 слив, Нина - 4. Сколько всего слив сорвали Дима и Нина вместе?

б) Из коробки взяли 6 красных карандашей и 4 синих. Сколько всего карандашей взяли из коробки?

8.   Объясните с теоретико-множественной точки зрения смысл выражений: а) 8 - 3; б) 4 - 4; в) 4 - 0.

9.       Объясните, почему нижеприведенные задачи решаются при помощи вычитания.

а) В корзине было 7 морковок, 3 из них отдали кроликам. Сколько морковок осталось?

б) На столе 8 чашек, их на 3 больше, чем стаканов. Сколько стаканов на столе?

в) На верхней полке шкафа 7 книг, а на нижней 4. На сколько книг больше на верхней полке, чем на нижней?

10.   Обоснуйте выбор действий при решении задач.

а) На одной полке 5 книг, на другой на 3 больше. Сколько книг на двух полках?

б) Во дворе гуляли 6 мальчиков, а девочек на 2 меньше. Сколько всего детей гуляло во дворе?

11.   Запишите, используя символы, правило вычитания суммы из числа и дайте его теоретико-множественное истолкование.

12.   Используя определение произведения чисел через сумму, объясните, каков теоретико-множественный смысл произведения 2 ´ 4.

13.   Раскройте теоретико-множественный смысл произведения 2 ´ 4, используя определение произведения чисел через декартово произве­дение множеств.

14.   Объясните, почему следующие задачи решаются при помощи умножения.

а) На каждую из трех тарелок положили по 2 яблока. Сколько всего яблок положили?

б) Школьники посадили в парке 4 ряда деревьев, по 5 штук в ряду. Сколько деревьев они посадили?

16.   Используя теоретико-множественный смысл действий над числами, обоснуйте выбор действий при решении задач.

а) Первоклассники заняли в кинотеатре 3 ряда, второклассники - 4 ряда, а третьеклассники - 5 рядов. Сколько учеников начальных клас­сов было в кинотеатре, если в каждом ряду они занимали по 9 мест?

б) В саду 8 рядов деревьев, по 9 в каждом. Из них 39 яблонь, 18 груш, остальные сливы. Сколько сливовых деревьев в саду?

17.   Какие рассуждения учащихся вы будете считать правильными при выполнении ими следующих заданий.

а) Вера и Надя сажали тюльпаны. Вера посадила 8 рядов тюльпанов, по 9 в каждом, а Надя 9 рядов по 8 тюльпанов.

Можно ли, не выполняя вычислений, утверждать, что Вера посадила столько же тюльпанов, сколько Надя?

Пользуясь данным условием, объясните, что означают выражения: 72+ 72; 72×2; 8×9-8.

б) В гараже в 6 рядов стояло по 9 машин. Из каждого ряда выехало 8 машин. Сколько машин осталось в гараже?

18.   Объясните, что означают выражения, составленные по условию данной задачи: 9× 6; 8 × 2; 8 × 6; 9 - 8; (9 - 8) ×2; (9-8) × 6.

19.   Используя теоретико-множественный смысл частного, объясните смысл выражений: а) 10:2; б)5:1;  в) 5:5.

20.   Объясните, почему нижеприведенные задачи решаются при помощи деления. а) 15 редисок связали в пучки по 5 редисок в каждом. Сколько получилось пучков? б) 15 тетрадей раздали поровну 5 ученикам. Сколько тетрадей получил каждый?

21. Назовите отношения, которые рассматриваются в задачах, ре­шите задачи арифметическим методом, выбор действий обоснуйте.

а) Для украшения елки девочка вырезала 4 звездочки, а флажков в 3 раза больше. Сколько флажков вырезала девочка?

б) У Коли в 4 раза больше открыток, чем у Вовы. А у Лены их на 20 меньше, чем у Коли. Сколько открыток у Лены, если у Вовы их 7?

в) Миша поймал 48 окуней, Саша - на 6 меньше, чем Миша, а Коля - в 7 раз меньше, чем Саша. Сколько окуней поймали все мальчики?

22.   Какое правило является обобщением различных арифметических способов решения задачи. а) В коробке лежало 12 зеленых и 20 красных хлопушек. Все хлопушки раздали детям, по 4 каждому. Сколько ребят получили хлопушки? б) В лапту играли 8 девочек и 6 мальчиков. Они разделились на 2 команды. Сколько человек было в каждой команде?

 

Творческие задания

1.                     Докажите, что дистрибутивность умножения относительно сложения вытекает из равенства А ´ (В È С) = (А ´  В) È (А ´ С), а относительно вычитания - из равенства (А \ В) ´ С) = (А ´ В) \ (А ´ С).

2.                     Составьте сценарий практической работы для младших школьников по сравнению численностей множеств без их нахождения.

3.                     Проведите практическую работу, подтверждающую, что сумма 5 + 3 не зависит от выбора множеств, численности которых равны 5 и 3.

4.                     Докажите, что 0+0+…+0=0.

5.                     Докажите важное правило прибавления суммы к сумме, опираясь на теоретико-множественный подход к определению суммы: (a+b)+(c+d)=(a+c)+(b+d), (a+b)+(c+d)=(a+d)+(b+c)

6.                     Придумайте практическую работу по нахождению того, на сколько в одном множестве больше элементов (без нахождения их численности).

7.                     Опишите практическую работу в начальной школе, подтверждающую эквивалентность деления “на” и “по”. 

 

«Отношение делимости и его свойства»

 

Теоретическая часть

Вопросы к изучению

1.       Отношение делимости и его свойства.

2.       Признаки делимости.

3.       Наименьшее общее кратное и наибольший общий делитель.

4.       Простые числа.

5.       Способы нахождения наибольшего общего делителя и наименьшего общего кратного чисел.

 

Практическая часть

Обязательные задания

1.       Объясните, почему число 15 является делителем числа 60 и не яв­ляется делителем числа 70.

2.       Постройте граф отношения «быть делителем данного числа», заданного на множестве Х = {2, 6, 12, 18, 24}. Как отражены на этом графе свойства данного отношения?

3.       Известно, что число 24 - делитель числа 96, а число 96 – делитель числа 672. Докажите, что число 24 делитель числа 672, не выполняя деления.  

4.       Запишите множество делителей числа: а) 24; б)13; в)1.

5.       На множестве Х = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} задано отношение «иметь одно и то же число делителей». Является ли оно отношением эквивалентности?

6.       Докажите или опровергните следующие утверждения:

а) Если сумма двух слагаемых делится на некоторое число, то и каждое слагаемое делится на это число.

б) Если одно из слагаемых суммы не делится на некоторое число, то и сумма не делится на это число.

в) Если ни одно слагаемое не делится на некоторое число, то и сумма не делится на это число.

г) Если одно из слагаемых суммы делится на некоторое число, а другое не делится на это число, то и сумма не делится на это число.

7.       Верно ли, что: а) аM m и bM n Þ а bM mn;  б) аbM n Þ аM n или bM n.

8.       Выпишите из ряда чисел 132, 1050, 1114, 364, 12000 те, которые: а) делятся на 2; б) делятся на 4; в) делятся на 2 и не делятся на 4; г) делятся и на 2 и на 4.

10.   Верно ли утверждение:

а) Для того чтобы число делилось на 2, необходимо и достаточно, чтобы оно делилось на 4?

б) Для того чтобы число делилось на 2, достаточно, чтобы оно делилось на 4?

11.   Из ряда чисел 72,312,522,483, 1197 выпишите те, которые: а) делятся на 3; б) делятся на 9; в) делятся на 3 и не делятся на 9;

г) делятся и на 3 и на 9. Сделайте вывод о взаимосвязи делимости на 3 и на 9. Докажите его.

12.   Не выполняя сложения, установите, делится ли значение выраже­ния на 4:

а) 284+ 1440 + 113;               в)284+ 1441 + 113;

б) 284 + 1440 + 792224;        г)284 + 1441 + 113 + 164.

13.   Не выполняя вычитания, установите, делится ли разность на 9.

а) 360 - 144; б) 946 - 540; в) 30 240 - 97.

14.   Верно ли, что для делимости числа х на 8 в десятичной системе счисления необходимо и достаточно, чтобы на 8 делилось трехзначное число, образованное последними тремя цифрами десятичной записи числа х?

15.   Даны числа 36 и 45.

а) Найдите все общие делители этих чисел.

б) Можно ли назвать все их общие кратные?

в) Найдите три трехзначных числа, которые являются общими кратными данных чисел.

г) Чему равны D(36, 45) и K(36, 45)? Как проверить правильность полученных ответов?

16.   Верны ли записи: а) D(32, 8) =8 и K(32, 8) = 32; б)D (17,35)=1 и K(17,35)=595; в) D(255, 306) = 17 и K(255, 306) = 78030.

17.   Найдите K(а,b), если известно, что:

а) а = 47, b = 105 и D(47, 105) = 1; б) a = 315, b = 385 и D (315, 385) =35.

18.   Из множества чисел 1032, 2964, 5604, 8910, 7008 выпишите те, которые делятся на 12.

19.   Делятся ли на 18 числа 1548 и 942?

20.   К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.

21.   Найдите цифры а и b числа 72а-3 b, если известно, что это число делится на 45.

22.   Не выполняя умножения и деления уголком, установите, какие из следующих произведений делятся на 30: а)105×20;   б)47×12×5;   в)85×33×7.

23. Не выполняя сложения или вычитания, установите, значения каких выражений делятся на 36. а) 72+180+252; б) 612-432; в) 180+252+100; г)180+250+200.

24.   Из множества чисел 13, 27, 29; 51, 67 выпишите простые числа, а составные разложите на простые множители.

25.   Докажите, что число 819 не является простым числом.

26.   Разложите на простые множители числа 124, 588, 2700, 3780.

27.   Какое число имеет разложение: а)2³ × 3²× 7× 13;  б)2²× 3× 5³?

28. Найдите наибольший общий делитель и наименьшее общее кратное данных чисел, представив их в каноническом виде:  а) 948 и 624; б)120,540,418.

 

Творческие задания

1.       Докажите, что при любом натуральном n истинны утверждения:

а) n(n+ 1)(n+2) M 6; б) n(n+1)(n+2)(n+3) M 12.

2.       Сформулируйте признаки делимости на 12,15,18,36,45,75.

3.       Используя алгоритм Евклида, найдите наибольший общий делитель чисел. а) 846 и 246;   б) 585 и 1960;   в) 15283 и 10013.

4.       Верно ли, что: а) D(448, 656) = 16; б) K(578, 8670) = 8670?

5.       Докажите, что числа 432 и 385 взаимно простые.

6.       Найдите наибольший общий делитель всех пятизначных чисел, записанных при помощи цифр 1, 2, 3, 4, 5 (цифры в записи чисел не повторяются).

7.       Узнать, какой день недели будет 1 января 2020 г. (при условии, что действующий календарь сохранится).

8.       Найти остаток от деления на 3 числа А= -

9.       Доказать утверждения: 1) 0:а; 2) а:1; 3) если 1:а, то а=1.

 

 

Тема 2.2. «Системы счисления»

 

Теоретическая часть

1.                     Из истории возникновения и развития способов записи натуральных чисел и нуля.

2.                     Понятие системы счисления.

3.                     Позиционные и непозиционные системы счисления.

Запись и названия чисел в десятичной системе счисления

 

Практическая часть

Обязательные задания

1.   Запишите в десятичной системе счисления: XXVII,  XLIV, XXI,  LXII, LXXVIII, XCV, CDXXIII, MCDVII, MCDXIX, MDCCCLXXI.

2.   Запишите в римской системе счисления: 24, 117, 468, 1941, 1997, 2001.

3.   Запишите число в виде суммы разрядных слагаемых:  а) 4725; б) 3370; в) 10255.

4.   Какие числа представлены следующими суммами:  а) 6·10³+5·10+8; б) 7·10³+ 1·10; в) 8·10⁴+10³+3·10+1; г) 10⁵ + 10²?

5.   Напишите наибольшее трехзначное и десятизначное числа, в ко­торых все цифры различны.

6.   Решите арифметическим методом задачи из начального курса математики:

а) Сумма цифр двузначного числа равна 9, причем цифра десятков вдвое больше цифры единиц. Найдите это число.

б) Сумма цифр двузначного числа равна наименьшему двузначному числу. Цифра десятков обозначает число в 4 раза меньшее, чем цифра единиц. Какое это двузначное число?

Какие некорректности допущены в формулировках данных задач? Следует ли их исправлять?

7.   Каждая цифра пятизначного числа на единицу больше предыдущей, а сумма его цифр равна 30. Какое это число?

Творческие задания

1.       Выполните поиск решения задачи всеми способами. Решите задачу одним способом и проверьте, решив другим. Какие математические знания необходимы для решения данной задачи?  «На фабрике за три смены выработано 12840 м ткани. В первую смену выработали на 594 м больше, чем во вторую, а в третью - на 312 м меньше, чем в первую. Сколько мет­ров ткани выработали в каждую смену?».

2.       Решите задачу. Какой способ поиска арифметического решения задачи вы выбрали? «Рабочий выработал за смену в среднем 432 детали. Применив более рациональные спо­собы работы, он выработал в первый день 1528, а во второй день 2114 и в третий 2838 деталей. На сколько деталей и во сколько раз увеличилась средняя дневная выработка рабочего?».

3.       Постройте модель задачи и решите ее. «Три большие реки России Обь, Лена и Амур имеют общую длину 14206 км. Обь и Лена вместе имеют длину 9852 км, Лена и Амур - 8623 км. Какова длина каждой из этих рек?».

4.       Решите задачу. Какой метод решения задачи выбран? «Два автобуса отправились одновременно из города в спортивный лагерь, расстояние до которого 72 км. Первый автобус прибыл в лагерь на 15 мин. раньше второго. С какой скоростью шел каждый автобус, если скорость одного из них на 4 км в час больше другого?».

5.       Решите задачу и выполните ее проверку. «Двое мужчин купили для посадки 500 штук капустной рассады и заплатила поровну. На огороде у одного поместилось на 40 штук больше, чем у другого и он доплатил второму 8 грн. Сколько рассады посадил каждый и сколько стоил 1 десяток рассады?».

6.       Решите задачу арифметическим методом и выполните ее проверку. Методическое указание: при арифметическом способе решения задачи предположите, что все бревна сосновые. Сколько арифметических способов решения имеет данная задача? «На платформу погрузили 70 сосновых и еловых бревен общей массой 165 ц. Сосновое бревно имело массу 210 кг, а еловое - 250кг. Сколько было тех и других бревен?».

8.   Младшим школьникам предложена задача: «Запиши 5 четырехзначных чисел, используя цифры 2, 5, 0, 6 (одна и та же цифра не должна повторяться в записи числа)». А сколько вообще всевозможных четырехзначных чисел можно записать, используя цифры 2, 5, 0 и 6 так, чтобы одна и та же цифра не повторялась в записи числа?

 

 

«Алгоритмы арифметических действий»

 Теоретическая часть

Вопросы к изучению

1.   Запись числа в десятичной системе счисления

2.   Алгоритм сложения

3.   Алгоритм вычитания

4.   Теоретические основы алгоритмов умножения и деления

5.   Алгоритмы умножения и деления

 

Практическая часть

1.    На примере сложения чисел 237 и 526 покажите, какие теоретические факты лежат в основе алгоритма сложения многозначных чисел.

2.    При изучении алгоритма сложения трехзначных чисел в начальной школе последовательно рассматриваются такие случаи сложения: 231 + 342; 425 + 135; 237 + 526; 529 + 299. Каковы особенности каждого из этих случаев?

3.    Вычислите устно значение выражение; использованный прием обоснуйте:

              а) 2746 + 7254 + 9876;           б) 7238+8978+2768;

              в) (4729 + 8473) + 5271;         г) 4232 + 7419 + 5768 + 2591;

                          д) (357 + 768 + 589) + (332 + 211 + 643).                    

4.    Какие рассуждения школьников вы будете считать правильными при выполнении задания.

а) Можно ли утверждать, что значения сумм в каждом столбике одинаковы:

 2459+121                    53075+2306

 2458+122                    53076+2305

 2457+123                    53006+2375

 2456 + 124                  53306+2075                

б) Можно ли записать значения этих сумм в порядке возрастания:  4583+321       4593+311       4573+331

5.    На примере нахождения разности чисел 469 и 246, 757 и 208 проиллюстрируйте теоретические основы алгоритма вычитания чисел столбиком.

6.    Выполните вычитание, используя запись и объясняя каждый шаг алгоритма: а)84072 - 63894; б)940235-32849; в)935204 - 326435; г) 653481 - 233694.

7.    Сколько пятизначных чисел можно записать, используя цифры 1 и 0? Чему равна разность между наибольшим и наименьшим из этих пятизначных чисел?

8.    Назовите способы проверки правильности вычитания многозначных чисел и дайте им обоснование.

9.    Вычислите (устно) значение выражения, использованные приемы  обоснуйте: а)2362-(839+1362); б)(1241+576)-841 в)(7929+5027+4843)-(2027+3843).

10.                  На примере умножения числа 357 на 4 проиллюстрируйте теоретические основы алгоритма умножения многозначного числа на однозначное.

11.                 На примере умножения 452 на 186 проиллюстрируйте теоретические основы алгоритма умножения многозначного числа на многозначное.

12. Решение задачи запишите в виде числового выражения, а затем найдите его значение:

а) На элеватор отвезли 472 т овса, ржи на 236 т больше, чем овса, пшеницы в 4 раза больше, чем овса и ржи вместе. Сколько тонн пшеницы отвезли на элеватор?

б) Столяр делает в день 18 рам, а его помощник на 4 рамы меньше. Сколько рам они сделают за 24 дня, если каждый день будут работать, вместе?

13. Как могут рассуждать учащиеся, выполняя следующее задание: «Ширина земельного участка прямоугольной формы равна 24 м. Это в 6 раз меньше его длины. Объясни, что обозначают выражения, записанные по условию задачи, и вычисли их значения: 24× 6; 24× (24 × 6); (24 + 24 × 6) × 6; 24 × 2; 24 × 2 + 24 × 6 × 2».

14.      Выполните умножение чисел, используя запись столбиком, и объясняя каждый шаг алгоритма: а) 984 × 27; б)7040 × 234; в)8276 × 73; г)4569 × 357.

15.      Используя свойства умножения, найдите наиболее рациональ­ным способом значение выражения:

а) 8 × 13 × 4 × 125 × 25;            г)124× 4 + 116× 4;

б) 24×(27×125);                        д) (3750-125) ×8;

в) (88 + 48) ×125;                    е)1779×1243 – 779×1243.

16. Зная, что 650×34 = 22100, найдите произведение чисел, не выполняя умножения столбиком: а) 650×36; б)650×32;  в) 649×34.

17. Найдите и обоснуйте приемы умножения 24 на 35 и, пользуясь ими, умножьте на 35 числа: 12, 18, 24, 32, 48, 64.

18.      Вычислите рациональным способом значение выражения:

а) (420-394) × 405 – 25 × 405; б) 105 × 209 + (964 - 859) × 209 × 400.

19.      Найдите значения выражений 13 ×11, 27 ×11, 35 ×11, 43 ×11, 54 ×11. Верно ли: чтобы найти результат умножения двузначного числа на 11 в случае, когда сумма цифр двузначного числа меньше 10, достаточно между цифрами данного числа написать число, равное сумме его цифр?

20.      Найдите значение выражений 29 × 11, 37 × 11, 47 × 11, 85×11, 97 × 11. Верно ли: чтобы найти результат умножения двузначного числа на 11 в случае, когда сумма цифр двузначного числа больше или равна 10, достаточно между цифрой десятков, увеличенной на 1, и цифрой единиц написать число, равное разности между суммой его цифр и чис­лом 10?

21.      Не выполняя деления, определите число цифр частного чисел:

а) 486 и 7;  б) 7243 и 238;в) 5792 и 27; г) 43126 и 543.               

22.      На примере деления числа 867 на 3 проиллюстрируйте теоретические основы алгоритма деления трехзначного числа на однозначное.

23.      Обоснуйте процесс деления уголком а на b , если  а) а = 4066, b = 38; б) а = 4816, b  = 112.  

24.      Как, не вычисляя, можно установить, что деление выполнено неправильно, если: а) 51 054:127 = 42; б) 405945:135 = 307?

25.      Не вычисляя значений выражений, поставьте знаки > или <, чтобы получились верные неравенства. 

а) 1834:7 … 783:9; б) 8554:91 ...7488:72; в) 137532:146 ... 253242:198;            г) 7248:6 ...758547:801.

26. Не производя деления, разбейте данное выражение на классы при помощи отношения «иметь в частном одно и тоже число цифр»: а)20700:300; б)20300:700; в) 5460:60; г) 14 640 : 80; д) 30 720:40;  е) 1500:300.

27. Решение задачи запишите в виде числового выражения, а затем найдите его значение.

а) Туристы совершили экскурсию по реке на катере, проплыв всего 66 км. Сначала 2 ч они плыли со скоростью 18 км/ч, а остальной путь - со скоростью 15 км/ч. Сколько всего часов находились в пути туристы?

б) Печенье упаковали в пачки по 250 г. Пачки сложили в ящик в 4 слоя. Каждый слой имеет 5 рядов по 6 пачек в каждом. Определите массу сложенного в ящик печенья.

28.                 Найдите значение первого выражения, а затем используйте его при вычислении значения второго.

а) 45120: (376×12),  б) 241×(1264:8), в) 45120: (376×3); г) 241×(1264:4).

29.                 Найдите двумя способами значение выражения:  а) (297+405+567):27; б) 56×(378:14); в) (240×23); 48; г) 15120:(14×5×18).

30.                 Найдите значение выражения:

а) 8919:9+114240:21      б)1190-35360:34+271;

в) 8631-(99+44 352:63)   г) 48 600×(5 045-2 040): 243- (86043:43 +504) ×200;

д) 4880×(546+534): 122-6390×(8 004-6924) ×213.

 

Творческие задания

1.          Докажите, что а + (b – с) =   

2.          Используя это правило, вычислите значение выражения:

а) 6420+(3580-1736); б) 5480 + (6290 - 3480).

3.          Докажите, что а – ( b - с) =

4.   Используя это правило, вычислите значение выражения: а) 3720-(1742-2678), б) 2354-(965-1246).

5.          Докажите, что (а – в) – с =

6.   Используя это правило, вычислите значение выражения: а) (4317-1928)-317; б) (5243-1354)-1646.

7.          Объясните, почему нижеприведенные задачи решаются при помощи умножения чисел и решите их.                         

а) Земля при обращении вокруг Солнца за сутки проходит примерно 2 505 624 км. Какой путь проходит Земля за 365 дней?

б) В школу привезли 56 пачек книг, по 24 книги в каждой пачке.  Сколько всего книг привезли в школу?   

8.          Объясните, почему следующие задачи решаются при помощи деления чисел, и решите их.

а) В 125 коробок разложили поровну 3000 карандашей. Сколько карандашей в каждой коробке?

б) Расфасовали 12 кг 600 г конфет в коробки по 300 г в каждой. Сколько коробок конфет получилось?

 

 

 

ВОПРОСЫ К КОЛЛОКВИУМУ

1.       Из истории возникновения понятия натурального числа.

2.       Порядковые и количественные натуральные числа. Счет.

3.       Теоретико-множественный смысл количественного натурального числа и нуля.

4.       Теоретико-множественный смысл отношения «меньше», «равно»

5.       Теоретико-множественный смысл суммы.

6.       Законы сложения.

7.       Теоретико-множественный смысл разности.

8.       Отношения «больше на» и «меньше на».

9.       Правила вычитания числа из суммы и суммы из числа.

10.   Из истории возникновения и развития способов записи натуральных чисел и нуля.

11.   Понятие системы счисления.

12.   Позиционные и непозиционные системы счисления.

13.   Запись и названия чисел в десятичной системе счисления.

14.   Сложение в десятичной системе счисления.

15.   Умножение в десятичной системе счисления

16.   Упорядоченность множества натуральных чисел.

17.   Вычитание в десятичной системе счисления.

18.   Деление в десятичной системе счисления.

19.   Множество целых неотрицательных чисел.

20.   Отношение делимости и его свойства.

 

 

Тема 2.3. «Правила приближенных вычислений»

 

Вопросы к изучению:

1.     Какие числа называются приближенными?

2.     Какие цифры называются значащимися?

3.     Какие цифры называются сомнительными?

4.     Какие дроби называются периодическими?

5.     Способы записи приближенных чисел.

6.      

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ:

Пример 1:  Определите значение 2а, если а=25±0,02

Решение:    2а=25∙2±0,02∙2                     2а=50±0,04

Пример 2: Определите произведение чисел:   а=10±0,1    и    b=100±0,5

Решение:    Р=10+100=110      ∆р=110 ∙                       а∙b= 110 ± 1,65

Пример 3: Вычислите    , если х=47,2±0,5         у=19,4±0,1

Решение:                      ∆u=2,43∙

                   u=2,43±0,039 или  после округления u=2,43±0,04

Вычисление без строгого учета погрешностей

При массовых вычислениях, когда не учитывается погрешность каждого промежуточного результата, используют правило подсчета верных цифр.

Пример 4.  Сложите приближенные числа     

 2,369     17,24       8,653     94,124

Решение: округляем до сотых долей               

 2,37       17,24      8,65        94,12         2,37+17,24+8,65+94,12=122,38≈122,4

Пример 5: Умножьте приближенные числа:    23,41    и    0,0324

Решение:   Выполняется точное умножение     23,41∙0,0324=0,758484≈0,758

Пример 6:  Вычислите   a=2030±40, b=0.042±0.0005, c=2.3047±0.00005, d=21394±70,  k=0.300±0.0005

Решение:

Представим числа в стандартном виде

a=2030±40    b=0.042±0.0005   c=2.3047±0.00005     d=21394±70      k=0.300±0.0005

   2,0∙10³         4,2∙10^-2            2,3047∙10⁰          2,1394∙10⁴        3,00∙10^-1

   2,0∙10³         4,2∙10^-2            2,30∙10⁰              2,14∙10⁴            3,00∙10^-1

 

 

ПРАКТИЧЕСКАЯ ЧАСТЬ:

Задание 1. Найдите сумму, разность, произведение и частное приближенных чисел

a)     а1=25,74±0,2          а2=96,42±0,3

b)    а1=37,375±0,03      а2=3,042±0,004

c)     а1=879,03±0,1        а2=653,84±0,4

 

Задание 2.   Для сторон прямоугольника найдены значения а=2,56±0,005    и    b=1,2±0,02. Найдите его площадь и периметр.

 

Задание 3. Выполните действия, округляя промежуточные результаты до 4 цифр  и сравните результаты:

(0,364+0,423)∙0,125              и            0,364∙0,125+0,423∙0,125

 

Задание 4. Найдите сумму приближенных чисел 3454,70, 386,350,   32,4350,   1,24430 по правилу подсчета цифр.

 

 Задание 5. Вычислите:

a)      a=231,05±0,02, b=43±2, c=27,81±0.003, d=321±20,  k=843,44±0.03

b)     a=2,4∙10^-3, b=2,03∙10⁴, c=4,34∙10^-5, d=8,2∙10³

 

 

 

Тема 2.4.  «Величины и их измерение

 

Теоретическая часть

Вопросы к изучению

1.   Понятие положительной скалярной величины и ее измерения.

2.    Действия с положительными скалярными величинами.

3.   Измерение величин в практической деятельности.

4.   Стандартные единицы величин.

 

Практическая часть

1.   О каких величинах идет речь в следующих предложениях:

а) Груши дороже яблок.

б) Книга тяжелее тетради.

в) Таня выше Светы.

2.   Какие величины могут характеризовать следующие объекты:

а) карандаш;  б) человек; в) озеро?

3.   Имеются два куска проволоки. Каким образом можно сравнить их длины, не прибегая к измерению? Какими могут быть результаты сравнения?

4.   Как можно сравнить массы двух предметов, не определяя массу каждого из них? Какими могут быть результаты сравнения?

5.   На рисунке 1 изображены два прямо­угольника, имеющие площади А и В.

                                А                         В

 

 

 

Постройте прямоугольник, площадь которого равна: а) А+В; б) 3×А;  в)×В; г) В–А.

6.   Разбейте на классы тремя способами сле­дующие величины:

А - высота дерева;        М - площадь доски;

В - 16кг;                          Н – 13с;

С - масса доски;            К - 26м;

Д - 25 см;                        L - длина веревки;

Е - возраст дерева;       Р - толщина доски.

7.   Назовите стандартные единицы, с помощью которых можно измерить величины, указанные в таблице. Запишите их.

8.                     О каких величинах идет речь в следующих предложениях:

а) В одной коробке 25 яблок, а в другой 30 яблок.

б) 15 яблок дороже, чем 8 груш.

в) В одном ящике 20 кг овощей, а в другом 12 кг овощей.

9.                     Какие из данных величин можно сравнить между собой:

1500м;           2,5 км;             18 штук;                8 десятков;

3ц;                 1км 500м;        299 кг;                   18 пар.

10.                 Сравните величины:

а) 56 мин и ч;                           б) м  и   дм;

в) 1,5 см и дм;                            г) кг   и   1250 г.    

11.                 Назовите объект, его величину, численное значение и единицу измерения величины в каждом из следующих предложений:

а) В коробке 8 кг яблок.

б) Глубина оврага 2 м.

в) Площадь садового участка 6 соток.

г) В сервизе 6 тарелок.

д) Рост девочки 1 м 20 см.

12.                 Назовите величины и объекты, о которых говорится в задаче:

а) За тетради заплатили х р., а за карандаши на t р. меньше. Сколько стоили карандаши?

б) Мешок картофеля тяжелее ящика с луком на 2 кг. Какова масса мешка картофеля, если масса ящика с луком z кг?

в) На первой полке стояло х книг. На второй на у книг больше, а на третьей на y книг меньше, чем на первой полке. Сколько книг стояло на трех полках?

13.                 Назовите величины, о которых говорится в задаче, и действия с ними, которые будут выполнены в процессе решения:

а) В ящике было 24 кг апельсинов. Сначала из него взяли 5 кг, а потом в 3раза больше, чем в первый раз. Сколько апельсинов осталось в ящике?

б) Для вышивания первого узора нужно 24 м ниток, для второго в 6 раз меньше, а для третьего - на 16м больше, чем для первого. Хватит ли 7 катушек для вышивания всех узоров, если в каждой катушке по 10 м ниток?

14.                 Решите задачи, предварительно установив, в чем их сходство и различие:

а) Со склада отправили в столовую и в магазин 8 машин с овощами. Магазин получил 24 т овощей, а столовая - в 3 раза меньше. Сколько машин с овощами отправили в магазин и сколько в столовую, если масса овощей в каждой машине была одинаковой?

б) Со склада отправили в столовую и в магазин несколько машин с овощами. Масса овощей в каждой машине была одинаковой. Магазин получил 24 т овощей, а столовая - в 3 раза меньше. Сколько машин с овощами отправили со склада, если в столовую отправили 2 машины?

 

«Геометрические величины»

 

Теоретическая часть

Вопросы к изучению

1.                     Длина отрезка и ее измерение.

2.                     Величина угла и ее измерение.

3.                     Понятие площади фигуры и ее измерение.

4.                     Площадь многоугольника.

5.                     Площадь произвольной плоской фигуры и ее измерение.

 

 

Практическая часть

1.                     Отметьте на прямой три равных отрезка: АВ, ВС и СД. Чему будет равна длина каждого их этих отрезков, если за единицу длины будет выбрана длина отрезка: а) АВ; б) АС; в) АД?

2.                     Из одного куска проволоки, не разрезая его, надо сделать каркас: а) треугольной пирамиды; б) четырехугольной пирамиды; в) куба. Каж­дое ребро этих многогранников равно 1 см. Какова наименьшая длина такой проволоки?

3.                     Существуют ли на плоскости три точки А, В и С, такие, что:

а) АС= 15см, АВ=8см, ВС=7см;

б) АС = 8 см, АВ = 25 см, ВС = 40 см;

в) АС = 14 см, АВ = 30 см, ВС = 40 см?

4.                     Постройте отрезок, длина которого 4,6 Е. Каким будет числен­ное значение длины этого отрезка, если единицу длины Е:

а) увеличить в два раза; б) уменьшить в 1,5 раза?

5.                     Длину стола измеряли сначала в сантиметрах, потом в децимет­рах. В первом случае получили число на 108 больше, чем во втором. Чему равна длина стола?

6.                     Углы а и b- смежные. Чему равен каждый из них, если: а) один из них больше другого на 60°; б) один из них больше другого в 3 раза?

7.                     Внутри прямого угла провели луч. Вычислите градусную меру каждого из полученных при этом углов, если: а) один из них больше другого на 89°; б) один из них в 90 раз больше другого; в) половина одного из них равна трети другого.

8.                     Измерьте величину угла между указательным и средним пальца­ми руки при максимальном отклонении друг от друга.

9.                     Пусть а и b- смежные углы. Запишите формулу, которая связы­вает между собой величины этих углов. Какой функцией является зависимость одной из этих величин от другой? Какова область ее оп­ределения и область значения? Каким будет график этой зависимости?

10.                 Два угла величиной 40° и 50° имеют общую сторону. Какой угол могут образовывать другие их стороны? Ответьте на тот же вопрос, если даны углы 140° и 150°.

11.                 Углы ВАК и САМ - прямые. Угол САК равен 10°. Найдите величину угла ВАМ. Решите задачу в общем виде для произвольного по величине угла САК.

12.                 Площадь фигуры F равна сумме площадей фигур F₁ и F₂. Значит ли это, что фигура F составлена из фигур F₁ и F₂.

13.                 Два треугольника имеют равные площади. Следует ли из этого, что они равны?

14.                 Верно ли, что:

а) Численные значения площади одной и той же фигуры могут быть различными?

б) Численные значения неравных фигур могут быть равными?

в) Равновеликие фигуры равны?

15.                 Известно, что площадь фигуры 34,78 см². Каким будет численное значение площади этой фигуры, если измерить ее в квадратных деци­метрах?

16.                 Докажите, что площадь любого треугольника равна половине произведения его стороны на проведенную к ней высоту.

17.                 Площадь прямоугольника равна 12 см, длины его сторон выражаются натуральными числами. Сколько различных прямоугольников можно построить согласно этим условиям?

18.                 Прямые а и b параллельны. Точка В движется по прямой b, занимая положение B₁,B_2, B₃  и т.д., а точки A и С остаются неподвижными. Равновелики ли треугольники АB₁С, AB₂С и т.д.?

19.                 Длины сторон параллелограмма 6 и 12 см, а высота его, проведенная к меньшей стороне, 10 см. Найдите высоту, проведенную к большей стороне параллелограмма.

20.                 Докажите, что всякая трапеция равносоставлена с прямоугольником, одна сторона которого равна средней линии трапеции, а дру­гая ее высоте.

21.                 На фигуру F наложили палетку и подсчитали, что внутри фигура F содержится фигура, составленная из 28 единичных квадратов, а фигура F содержится внутри фигуры, состоящей из 35 единичных квадратов. Каково приближенное значение площади фигуры F?

22.                 Начертите круг радиуса 2 см на клетчатой бумаге и найдите его площадь, используя клетчатую бумагу как палетку, состоящую из квадратов со стороной, равной: а) 1 см;  б) 0,5 см.

23.                 Вычислите площадь этого круга по формуле, приняв p = 3,14. Сравните полученные результаты.

 

Раздел 3. Геометрические фигуры.

 

Тема 3.1. «Геометрические фигуры на плоскости»

 

Теоретическая часть

Вопросы к изучению

1.       История возникновения и развития геометрии.

2.       Свойства геометрических фигур на плоскости: углы.

3.       Параллельные и перпендикулярные прямые.

4.       Треугольники.

5.       Четырехугольники.

6.       Многоугольники.

7.       Окружность и круг.

8.       Роль геометрических построений в процессе изучения геометрии.

9.       Элементарные задачи на построение.

 

Практическая часть

Углы

1.       Назовите свойства угла, которые включены в его определение. Можете ли вы назвать другие свойства понятия “угол”?

2.       Вспомните определение биссектрисы угла. Как, не используя чертежных инструментов, найти биссектрису угла, вырезанного из бумаги?

3.       Сколько окружностей можно провести через: а) одну точку; б) две точки; в) три точки, не лежащие на одной прямой?

4.       Как расположены центры окружностей одного и того же радиу­са, проходящих через данную точку?

5.       Как расположены центры окружностей, проходящих через две данные точки?

6.       Окружность разделена в отношении 1:2:3, и точки деления соединены между собой отрезками. Определите углы полученного треугольника.

7.       Докажите, что все углы, опирающиеся на диаметр окружности прямые.

8.       Угол между двумя радиусами равен 150°. Определите угол между касательными, проведенными через концы этих радиусов.

9.       Как найти центр окружности, если он неизвестен?

10.   В данной окружности проведены два диаметра и концы их попарно соединены хордами. Докажите, что получившийся четырехугольник - прямоугольник.

11.   В каком месте открытого участка треугольной формы  нужно поместить фонарь, чтобы все три угла были одинаково освещены?

12.   В треугольной пластине нужно так просверлить отверстие, чтобы оно было равноудалено от ее сторон. Где находится центр этого отверстия?

13.   Стекольщику надо вырезать стекло для окна круглой формы. Как и что он должен измерить, чтобы вырезать нужное стекло, располагая только рулеткой.

14.   Острый угол между диагоналями прямоугольника 60°, меньшая его сторона 1,5 дм. Вычислите радиус окружности, описанной около этого прямоугольника.

15.   Угол при вершине равнобедренного треугольника 120°, боковая его сторона 4 дм. Вычислите диаметр окружности, описанной около треугольника.

Параллельные и перпендикулярные прямые

16.   Какие свойства параллельных прямых включены в их определе­ние и в аксиому параллельных?

17.   Как построить параллельные прямые с помощью линейки и чер­тежного треугольника? На каком признаке параллельности основано это построение?

18.   Верны ли следующие утверждения:

а) Если две прямые пересечены третьей, то соответственные углы равны.

б) Если при пересечении двух параллельных прямых третьей накрест лежащие углы равны, то эти две прямые параллельны.

19.   Как практически проверить, параллельны ли две данные пря­мые, начерченные на бумаге?

20.   Докажите, что две прямые, лежащие в одной плоскости и пер­пендикулярные к одной и той же третьей прямой, параллельны между собой.

21.   Углы АВС и СВD - смежные, угол СВD равен . Определите угол между перпендикуляром, проведенным из точки В к прямой АD, и биссектрисой угла АВС.

Треугольники

22.   Можно ли из палочек длиной 10 см, 6 см, 4 см сложить треугольник?

23.   Как установить, равны два треугольника или нет?

24.   Назовите свойства равнобедренного треугольника. Какие из них содержатся в определении, а какие надо доказывать?

25.   Отвечают ли требованиям, предъявляемым к определениям понятий, следующие формулировки: а) Треугольник, у которого две стороны и два угла равны, называется равнобедренным. б) Средней линией треугольника называется прямая, проходящая через середины двух его сторон. в) Средней линией треугольника называется отрезок, соединяющий середины двух его сторон и параллельный основанию.

26.   Могут ли равносторонние треугольники быть: а) прямоугольными; б) тупоугольными? Ответ обоснуйте.

27.   Установите вид треугольника (по углам), если один из его внутренних углов: а) равен сумме двух других; б) больше суммы двух других; в) меньше суммы двух других.

28.   Можно ли какой-нибудь треугольник разрезать на два остроугольных?

29.   Прямая р пересекает отрезок А В в точке О, являющейся его серединой. Докажите, что точки A и В находятся на одинаковом расстоянии от прямой р.

30.   Отрезки АВ и СО пересекаются в точке О, являющейся серединой каждого. Докажите, что АС и ВО параллельны.

31.   Столяру нужно заделать отверстие треугольной формы. Какие он должен снять размеры, чтобы изготовить латку? Что он должен измерить, если отверстие имеет форму: а) прямоугольного треугольника; б) равностороннего треугольника?

Четырехугольники

32.   Постройте параллелограмм АВСD и его высоты, выходящие из вершины С.

33.   Обоснуйте следующий способ построения параллелограмма, предложенный младшим школьникам: «Проведи две пересекающиеся прямые. При помощи циркуля отложи на одной прямой от точки пересечения равные отрезки. Затем на другой прямой таким же образом отложи равные отрезки (не обязательно такой же длины, что и на первой прямой). Получится параллелограмм».

34.   Докажите, что всякий параллелограмм, у которого диагонали равны, есть прямоугольник.

35.   Мастерская изготовила пластины четырехугольной формы. Как проверить, будет ли пластина иметь форму прямоугольника, располагая лишь линейкой с делениями.

36.   Мастеру надо изготовить щит, который должен полностью закрыть нишу прямоугольной формы. Какие он должен снять размеры, чтобы изготовить этот щит?

37.   Докажите, что параллелограмм, диагонали которого взаимно перпендикулярны, является ромбом.

38.   Докажите, что почтовый конверт склеивается из листа бумаги, имеющей форму ромба (припуски на склеивание не учитывать).

39.   Паркетчик, проверяя, имеет ли выпиленный четырехугольник форму квадрата, убеждается, что диагонали равны и пересекаются под прямым углом. Достаточна ли такая проверка?

40.   Столяру нужно изготовить подставку в форме четырехугольника. Какие размеры должен он иметь для выполнения заказа? Что должен измерить столяр, если подставка имеет форму: а) параллело­грамма; б) прямоугольника; в) ромба; г) квадрата?

41.   Докажите, что средняя линия трапеции параллельна основаниям и равна их полусумме.

42.   Докажите, что отрезки прямых, соединяющих середины смежных сторон равнобедренной трапеции, образуют ромб.

43.   Земельный участок, имеющий форму трапеции, отдан под спортивный городок. Какие размеры должен снять землемер, чтобы начертить план этого участка?

Многоугольники

44.   Сформулируйте определение простой замкнутой ломаной и постройте такую фигуру.

45.   Расстояние от пункта А до пункта В равно 3 км, а от пункта В до пункта С вдвое больше. Каково наибольшее и наименьшее расстояние от пункта А до пункта С?

46.   Могут ли все углы выпуклого четырехугольника быть: а) тупыми; б) острыми; в) прямыми?

47.   Сколько прямых углов может иметь: а) параллелограмм; б) трапеция?

48.   Дан квадрат, разрезанный по диагонали на два треугольника. Сколько выпуклых многоугольников, отличных от квадрата, можно составить из этих треугольников?

49.   Квадрат разрезан по своим диагоналям. Сколько выпуклых многоугольников, отличных от квадрата, можно составить из четырех образовавшихся треугольников?

50.   Разрежьте по диагонали произвольный прямоугольник и из полученных треугольников составьте всевозможные выпуклые многоугольники.

51.   Назовите свойства правильного многоугольника. Можете ли вы привести пример многоугольника, не являющегося правильным, но имеющего: а) все равные между собой углы; б) все равные стороны?

52.   Сколько сторон имеет многоугольник, если сумма его внутренних углов равна 40d?

53.   Можно ли сложить паркет из правильных: а) треугольников, б) пятиугольников; в) восьмиугольников; г) восьмиугольников и квадратов?

Круг и окружность

54.   Сколько окружностей можно провести через: а) одну точку; б) две точки; в) три точки, не лежащие на одной прямой?

55.   Как расположены центры окружностей одного и того же радиуса, проходящих через данную точку?

56.   Как расположены центры окружностей, проходящих через две данные точки?

57.   Окружность разделена в отношении 1:2:3, и точки деления соединены между собой отрезками. Определите углы полученного треугольника.

58.   Докажите, что все углы, опирающиеся на диаметр окружности, прямые.

59.   Угол между двумя радиусами равен 150°. Определите угол между касательными, проведенными через концы этих радиусов.

60.   Как найти центр окружности, если он неизвестен?

61.   В данной окружности проведены два диаметра и концы их попарно соединены хордами. Докажите, что получившийся четырехуголь­ник - прямоугольник.

62.   В каком месте открытого участка треугольной формы нужно поместить фонарь, чтобы все три угла были одинаково освещены?

63.   В треугольной пластине нужно так просверлить отверстие, чтобы оно было равноудалено от ее сторон. Где находится центр этого отверстия?

64.   Стекольщику надо вырезать стекло для окна круглой формы. Как и что он должен измерить, чтобы вырезать нужное стекло, располагая только рулеткой.

65.   Острый угол между диагоналями прямоугольника 60°, меньшая его сторона 1,5 дм. Вычислите радиус окружности, описанной около этого прямоугольника.

66.   Угол при вершине равнобедренного треугольника 120°, боковая его сторона 4 дм. Вычислите диаметр окружности, описанной около треугольника.

 

Задачи на построение:

1.       Постройте с помощью циркуля и линейки сумму и разность двух данных: а) отрезков; б) углов.

2.       Разделите данный угол на 4 равные части.

3.       Дан треугольник АВС. Постройте другой, равный ему, треугольник АВС.

4.       Постройте окружность данного радиуса, проходящую через две данные точки.

5.       Постройте с помощью циркуля и линейки треугольник по из­вестным трем сторонам. Всегда ли такое построение возможно?

6.       Даны отрезок р, два угла а и b. Всегда ли можно построить треугольник, у которого сторона равна р, а прилежащие к ней углы равны а и b.

7.       Постройте с помощью циркуля и линейки прямоугольник, у которого известны его стороны а и b.

8.       Пользуясь только циркулем и линейкой, постройте: а) прямоугольник по диагонали и одной из сторон; б) квадрат со стороной p; в) квадрат, диагональ которого задана.

9.       Сколько можно построить параллелограммов с вершинами в трех данных точках, не лежащих на одной прямой?

10.   Постройте параллелограмм, если известны его диагонали и угол между ними.

11.   Сколько параллелограммов можно построить, если известны две его соседние стороны? Ответ обоснуйте.

12.   С помощью циркуля и линейки постройте ромб по: а) известным диагоналям; б) известной стороне и одному из углов при его вершине;  в) углу и диагонали, исходящей из вершины этого угла; г)стороне и диагонали.

13.   Постройте трапецию по основаниям и боковым сторонам.

14.   По каким данным можно построить равнобедренный треугольник? Во всех возможных случаях выполните построения.

 

 

Тема 3.2. «Геометрические фигуры в пространстве»

 

Теоретическая часть

Вопросы к изучению

1.                     Свойства параллельного проектирования.

2.                     Многогранники их изображение.

3.                     Шар, цилиндр, конус и их изображение.

 

Практическая часть

1.                     Верно ли, что при параллельном проектировании проекцией параллелограмма будет произвольный параллелограмм?

2.                     Каким будет при параллельном проектировании изображение прямоугольника? ромба? квадрата?

3.                     Как найти при параллельном проектировании проекцию точки пересечения высот равностороннего треугольника?

4.                     Изобразите на листе бумаги: а) прямую призму, основаниями которой являются правильные шестиугольники; б) параллелепипед; в) правильную пирамиду, основанием которой является квадрат.

5.                     Проверьте, выполняется ли теорема Эйлера для четырехугольной: а) призмы; б)пирамиды.

6.                     Выпуклый многогранник имеет 6 вершин и 8 граней. Найдите число ребер и изобразите этот многогранник.

7.                     Выпуклый многогранник имеет 8 вершин и 6 граней. Найдите число ребер и изобразите его.

8.                     Изобразите на листе бумаги шар и параллельную проекцию шара.

9.                     Изобразите на листе бумаги конус.

10.                 Изобразите на листе бумаги: а) прямую призму, основаниями которой являются правильные шестиугольники; б) параллелепипед; в) правильную пирамиду, основанием которой является квадрат.

11.                 Проверьте, выполняется ли теорема Эйлера для четырехугольной: а) призмы; б) пирамиды.

12.                 Выпуклый многогранник имеет 6 вершин и 8 граней. Найдите число ребер и изобразите этот многогранник.

13.                 Выпуклый многогранник имеет 8 вершин и 6 граней. Найдите число ребер и изобразите его.

 

 

 

3.3Задания для проведения промежуточной аттестации по дисциплине

Оценка освоения дисциплины предусматривает проведение дифференцированного зачета.

 

Комплект тестовых заданий

для проведения дифференцированного зачёта

                                          

 

Билет 1

1. Раскройте понятия: множество, элементы множества, операции над множествами. Перечислите способы задания множеств.

2. Придумайте задания для детей (возраст определите сами), в процессе выполнения которых они будут находить объединение, пересечение, дополнение множеств.

 

Билет 2

1. Раскройте понятия: множество, отношения между множествами.

2. Придумайте задания для детей (возраст определите сами), в процессе выполнения которых они будут устанавливать взаимно-однозначное соответствие между множествами.

 

Билет 3

1. Раскройте понятия: множество, разбиение множества на классы, соответствия между множествами.

2. Придумайте задания для детей (возраст определите сами), в процессе выполнения которых они будут выполнять: а) разбиение множества на классы; б) упорядочивание множества.

 

Билет 4

1. Раскройте понятия: величина, свойства однородных величин, измерение величин, длина, ее измерение, свойства.

2. Придумайте задания для детей (возраст определите сами), в процессе выполнения которых они будут выявлять свойства длины отрезка.

 

Билет 5

1. Раскройте понятия: величина, свойства однородных величин, измерение величин, площадь фигуры, ее измерение, свойства

2. Придумайте задания для детей (возраст определите сами), в процессе выполнения которых они будут выявлять свойства площади фигуры.

 

Билет 6

1. Раскройте понятия: величина, свойства однородных величин, измерение величин, объем, его измерение, свойства.

2. Придумайте задания для детей (возраст определите сами), в процессе выполнения которых они будут выявлять свойства объема тела.

 

Билет 7

1. Раскройте понятие геометрической фигуры на плоскости. Представьте виды величин, свойства величин.

2. Придумайте диалог с детьми (возраст определите сами), раскрывающий существенные свойства плоских геометрических фигур: круга, квадрата, треугольника, прямоугольника.

 

Билет 8

1. Раскройте понятие геометрической фигуры в пространстве, представьте их виды и свойства.

2. Придумайте игровые упражнения и диалоги к ним для детей (возраст определите сами) распознавание геометрических тел (шара, куба, цилиндра, конуса, призмы) и раскрытие их свойств.

 

Билет 9

1. Раскройте понятия: величина, свойства однородных величин, измерение величин, масса, ее измерение, свойства

2. Придумайте задания для детей (возраст определите сами), в процессе выполнения которых они будут выявлять свойства массы тела.

 

Билет 10

1. Раскройте понятия: величина, свойства однородных величин, измерение величин, длина, ее измерение, свойства.

2. Придумайте план обучения старших дошкольников измерению длины предмета (полосками).

 

Билет 11

1. Раскройте понятия: величина, свойства однородных величин, измерение величин, объем, его измерение, свойства.

2. Придумайте план обучения старших дошкольников измерению объема жидких или сыпучих веществ (стаканами).

 

Билет 12

1. Раскройте понятия: величина, свойства однородных величин, измерение величин, системы единых измерений.

2. Придумайте беседу с дошкольниками об общепринятых единицах измерений: метре, килограмме, литре.

 

Билет 13

1. Раскройте понятия: величина, свойства однородных величин, измерение величин. Назовите основные единицы системы единых измерений.

2. Приведите примеры старинных единиц измерений величин, встречающихся в быту и литературе. Расскажите об их происхождении и назовите их численное значение в единицах системы СИ.

 

Билет 14

1. Раскройте понятия: натуральные числа, свойства натурального ряда. Перечислите этапы развития понятия натурального числа.

2. Приведите примеры деятельности дошкольников в соответствии с историческими этапами развития понятия числа.

 

 

Билет 15

1. Раскройте понятия: натуральные числа, свойства натурального ряда, счет.

2. Назовите правила счета для ребенка в начальный период обучения и их изменения в последующем. Какие ошибки в счете, какими правилами вы предупреждаете?

 

Билет 16

1. Раскройте понятия: натурального числа, свойства натурального ряда. В чем заключается теоретико-множественный смысл натурального числа и нуля.

2. Придумайте диалог с дошкольниками для уточнения количественного и порядкового смысла числа.

 

Билет 17

1. Представьте натуральное число как результат измерения величины.

2. Придумайте беседу с дошкольниками о происхождении названий чисел второго десятка и круглых чисел в порядке ста.

 

Билет 18

1. Раскройте понятия: текстовая задача, ее структура. Представьте методы решения задач.

2. Придумайте простую текстовую задачу для дошкольников и раскройте работу над ней по всем этапам.

 

Билет 19

1. Раскройте понятие текстовая задача. Приведите основные этапы решения задач.

2. Придумайте составную текстовую задачу для дошкольников, решите ее различными методами и способами, предложите все возможные модели для ее решения.

 

Билет 20

1. Раскройте понятие математической модели. Приведите примеры моделирования в процессе решения задач.

2. Напишите диалог с ребенком (возраст определите сами), отражающий процесс решения конкретной задачи по этапам.

 

 

 

 Критерии оценивания:

В критерии оценки уровня подготовки студента входят:

·         уровень освоения студентом материала, предусмотренного учебной программой по дисциплине;

·         умения студента использовать теоретические знания при выполнении практических задач;

·         обоснованность, четкость, краткость и культура изложения ответа.

Уровень подготовки студента оценивается в баллах: 5 (отлично), 4 (хорошо), 3 (удовлетворительно), 2 (неудовлетворительно).

Оценка "отлично" ставится за исчерпывающий, точный ответ, демонстрирующий хорошее знание теоретического материала, умение использовать возрастные особенности детей для аргументации и самостоятельных выводов; свободное владение математической терминологией; анализ математического занятия в единстве содержания и формы; умение излагать материал последовательно, делать необходимые обобщения и выводы.

Оценка "хорошо" ставится за ответ, обнаруживающий хорошее знание и понимание теоретического материала, умение анализировать математическое занятие, приводя необходимые примеры, учитывающие возрастные особенности детей; умение излагать материал последовательно и грамотно. В задании может быть недостаточно полно развернута аргументация, возможны отдельные недостатки в формулировке выводов.

Оценка "удовлетворительно" ставится за ответ, в котором материал раскрыт в основном правильно, но недостаточно полно, с отклонениями от последовательности изложения, без учета возрастных особенностей детей. Анализ математического занятия подменяется пересказом, нет полноценных обобщений и выводов.

Оценка "неудовлетворительно" ставится, если ответ обнаруживает незнание теоретического материала и неумение его анализировать, в ответе отсутствуют необходимые математические примеры; нарушена логика в изложении материала, нет необходимых обобщений и выводов.

 

 

Условия организации и проведения дифференцированного зачета

 

Условия проведения дифференцированного зачета:

Дифференцированный зачет проводится одновременно для всей учебной группы. Ответы предоставляются письменно.

Количество вариантов задания для зачета равно числу студентов в группе.

Время выполнения задания - 1 час.

 Оборудование: бумага, ручки.

 

 

Скачано с www.znanio.ru