Муниципальное бюджетное общеобразовательное учреждение

«средняя общеобразовательная школа № 18 им. Р.С. Рамазанова»

Тема: "Угол между прямыми"

Цели:

Обучающие: с помощью практических заданий обеспечить понимание учащимися определения угла между пересекающимися, параллельными и скрещивающимися прямыми;

Развивающие: развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание; вырабатывать самостоятельность в освоении новых знаний.

Воспитательные: воспитывать у учащихся ответственное отношение к учебному труду, волевые качества; формировать эмоциональную культуру и культуру общения.

Тип урока:Изучение нового материала.

Методы: словесный (рассказ), наглядный (презентация), диалогический.

 Формируемые ууд:

 Предметные: владеть понятиями угла между двумя пересекающимися прямыми, угла между двумя параллельными прямыми, угла между двумя скрещивающимися прямыми, применять эти понятия к решению задач, распознавать перпендикулярные прямые. Личностные: формировать умение контролировать процесс своей математической деятельности.

Метапредметные: формировать умение сравнивать, анализировать, строить логическое рассуждение и делать выводы.

Планируемые результаты:

 учащийся овладеет понятиями угла между двумя пересекающимися прямыми, угла между двумя параллельными прямыми, угла между двумя скрещивающимися прямыми, научится применять эти понятия к решению задач, распознавать перпендикулярные прямые. Основные понятия Угол между двумя пересекающимися прямыми, угол между двумя параллельными прямыми, угол между двумя скрещивающимися прямыми, перпендикулярные прямые, перпендикулярные отрезки.

     I.            Организационный момент.

·        Приветствие.

·        Сообщение целей и задач урока.

·        Мотивация изучения нового материала.

·        Психолого-педагогическая настройка учащихся на предстоящую деятельность.

·        Проверка присутствующих на уроке;

 II.            Актуализация знаний.

Метод: фронтальный опрос (устно):

1.     Какие разделы изучает геометрия?

2.     Какие фигуры изучает планиметрия, а какие стереометрия?

3.     Каково взаимное расположение двух прямых в пространстве?

4.     Сколько углов образуется при пересечении двух прямых в пространстве?

5.     Как определить угол между пересекающимися прямыми?

Слад3

6.     Основание призмы ABCDA₁B₁C₁D₁ – трапеция. Какие из следующих пар прямых являются скрещивающими?

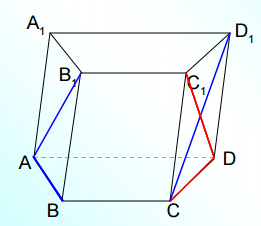
Ответ: ABи CC₁,A₁D₁и CC₁.

III.            Изучение нового материала.

Слайд 4

Расположение прямых в пространстве и угол между ними.

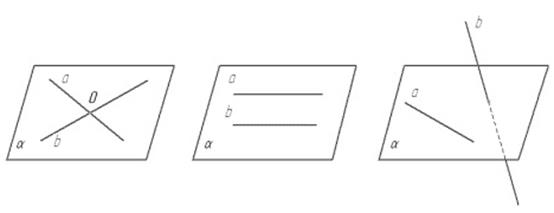
1.     Пересекающиеся прямые.

2.     Параллельные прямые.

3.     Скрещивающиеся прямые.

Слайд 5

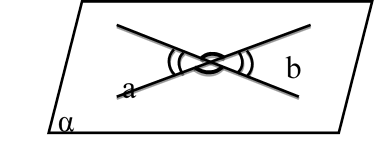
Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.

Слайд 6

Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.

Слайд 7

Угол между двумя параллельными прямыми равен 0°.

Слайд 8

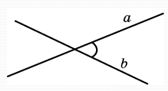Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.

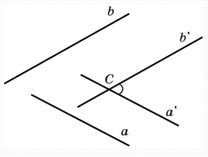
Слайд 9Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми и.

Слайд 10

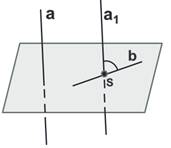Угол между скрещивающимися прямыми, как и между прямыми одной плоскости, не может быть больше 90°. Две скрещивающиеся прямые, которые образуют угол в 90°, называются перпендикулярными.

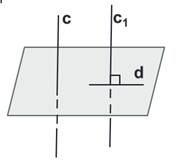
Слайд 11

Угол между скрещивающими прямыми.

Пусть ABи CD – две скрещивающиеся прямые.

Возьмём произвольную точку М₁ пространства и проведём через неё прямые А₁В₁ и C₁D₁, соответственно параллельные прямым AB и CD.

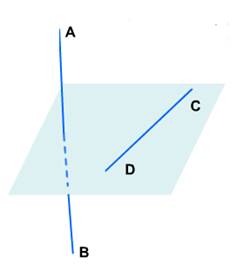
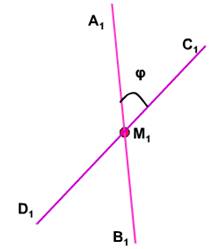
Если угол между прямыми А₁В₁ и C₁D₁равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ.

Слайд 12

Найдём угол между скрещивающимися прямыми ABи CD.

В качестве точки M₁можно взять любую точку на одной из скрещивающихся прямых.

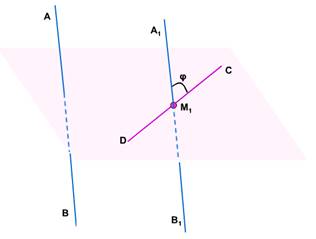
Слайд 13

Физкультминутка

Слайд 14

1. Покажите перпендикулярные скрещивающиеся прямые в окружении.

Слайд 15

2. Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.

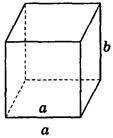а) 90°;  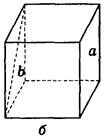                               б) 45°;

Слайд 16

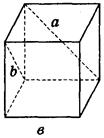в) 60°;  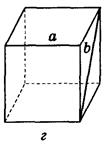                                г) 90°;

Слайд 17

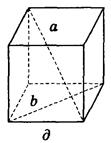д) 90°;  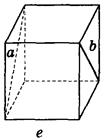                               е) 90°.

IV.            Закрепление нового материала

Слайд 19

Физкультминутка

Слайд 20

№1.

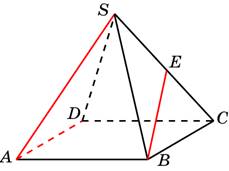В правильной пирамиде SABCD, все ребра которой равны 1, точка E– середина ребра SC.Найдите угол между прямыми ADи BE.

Решение:

Искомый угол = углу CBE.Треугольник SBC-равносторонний.

ВE – биссектриса угла = 60. Угол CBE равен 30.

Ответ:30°.

№263.

Какой угол называется углом между скрещивающими прямыми?

Ответ:

Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a₁и b₁, причем a₁ || a, b₁ || b.

№265.

Угол между прямымиaи bравен 90°. Верно ли, что прямые aи bпересекаются?

Ответ:

Неверно, так как прямые могут либо пересекаться, либо скрещиваться.

№267.

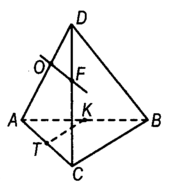DABC – тетраэдр, точка О и F – середины ребра AD и CDсоответственно, отрезок TK – средняя линия треугольника ABC.

a)     Чему равен угол между прямымиOFи CB?

b)    Верно ли, что угол между прямымиOFи TK равен 60°?

c)     Чему равен угол между прямымиTFи DB?

Решение:

Дано: DABC,

О – середина AD,

F – серединаCD,

ТК – средняя линия ∆АВС.

Решение:

a)     В плоскости АВС через точку С проходит прямая АС, параллельная прямой OF(т.к. OF – средняя линия ∆АВС, поэтому АСВ – угол между скрещивающимися прямыми OFт СВ. ∆АВС – правильный, поэтому АСВ=60°.
Ответ: 60°

b)    Т.к. OF || AC и TK || CB, то угол между  прямыми OF и TK равен углу между прямыми AC и CB, т.е. 60°.
Ответ: верно.

c)   Т.к. TF || AD (по свойству средней линии), то ADB=60°.
Ответ: 60°

  V.            Рефлексия

·        Что мы узнали нового?

·        Справились ли мы с теми задачами которые были заданы в начале урока?

·        Какие задачи мы научились решать?

VI.            Домашнее задание.

§4 (стр. 85-89), №268, №269.

Скачано с www.znanio.ru