Конспект "математическая грамотность как компонент функциональной грамотности школьников. Геометрия в природе"

Класс: 8.

Тема  «Геометрия в природе» формирование функциональной грамотности учащихся в ходе преподавания математики.

Тип урока: внеурочное мероприятие

Результаты:

Общеобразовательные:

-  Систематизировать знаний учащихся.

-  Повторить и закрепить сформированные ранее теоретические знания и учебные умения.

- Формирование у учащихся исследовательских умений устанавливать связи между понятиями, а также сравнивать и обобщать.

Развивающие:

-    Развитие устойчивого интереса к изучению математики.

- Формирование следующих качеств знаний учащихся: самостоятельность, глубина, осознанность, гибкость и устойчивость мышления.

- Формирование мыслительных операций (анализ и синтез, сравнение, аналогия, классификация и т.д.).

Воспитательные:

-  Формирование интереса к познанию.

- Формирование учебных умений по планированию, прогнозированию и моделированию результатов своей деятельности.

- Выявление широких возможностей более всестороннего воспитания учащихся на уроках математики.

Оборудование: раздаточный материал

Ход урока.

1 Организационный момент

Приветствие. Сегодня у нас не обычное занятие. Мы отправимся в поход в лес, не выходя из класса, и посмотрим где и как могут пригодиться знания геометрии.

2 Тема, цели и задачи

Вступительное слово учителя (2 мин.) 

экскурсию в лес, не выходя из класса, и посмотрим где и как

могут пригодиться  знания геометрии

Тема нашего сегодняшнего урока  «Геометрия вокруг нас». 

Скажите,  пожалуйста,  как    Вы  думаете,  какова  цель  нашего

урока  (учащиеся  высказывают  свое  мнение,  учитель

резюмирует).

Тема нашего сегодняшнего урока  «Геометрия в природе».

Скажите,  пожалуйста,  как    Вы  думаете,  какова  цель  нашего  урока?

Цель  урока  –  Применение  имеющихся  знании  в

нестандартной ситуации

3 Работа по теме мероприятия

И так,  мы в лесу

(слайд 1.(Лес),

Смотрите, какая высокая сосна, можем ли мы узнать ее высоту не применяя линейки и других измерительных инструментов?(слайд 2)

( слайд  2 (изображение высокой сосны)).

 Конечно, можем. Самый легкий и самый древний способ которым греческий мудрец Фалес в 6 в. до н.э. определил в Египте высоту пирамиды. Он воспользовался ее тенью. Фалес избрал день и час, когда длина его собственной тени равнялась его росту; в этот момент высота пирамиды также равнялась длине отбрасываемой ею тени.(слайд3)

                     слайд 3

Задача 1. В 40 м одна от другой растут две сосны. Вы измерили их высоту (допустим методом Фалеса): одна оказалась 31 м, другая, молодая – всего 6 м. Можете ли Вы вычислить, как велико расстояние между их верхушками. (По теореме Пифагора).

(Решается задача.)

Смотрите мы дошли до реки.(слайд 4)

 Не переплывая реки, измерить ее ширину – так же просто для знающего геометрию, как определить высоту дерева, не взбираясь на вершину. Недоступное расстояние измеряют следующим приемом: искомое расстояние заменяется определением другого расстояния, легко поддающегося непосредственному измерению.

Из многих способов решения этой задачи рассмотрим несколько наиболее простых. Причем первый способ мы разберем вместе, а еще несколько вы должны предложить сами.

Задача 2. Измерить ширину реки.

Решение:

1 способ.

Нам понадобится «прибор» с тремя булавками на вершинах равнобедренного прямоугольного треугольника

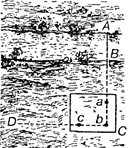Пусть требуется определить ширину АВ (слайд 7), стоя на том берегу, где точка В, и не перебираясь на противоположный. Став где-нибудь у точки С, держите булавочный прибор близ глаз так, чтобы, смотря одним глазом вдоль двух булавок, вы видели, как обе они покрывают точки В и А.

Слайд 7. Первое положение булавочного прибора.

Понятно, что, когда это Вам удастся, Вы будете находиться как раз на продолжении прямой АВ. Теперь, не двигая дощечки прибора, смотрите вдоль других булавок (перпендикулярно к прежнему направлению) и заметьте какую-нибудь точку D, покрываемую этими булавками, т.е. лежащую на прямой, перпендикулярной к АС. После этого воткните в точку С веху; покиньте прежнее место и идите с вашим инструментом вдоль прямой СD, пока не найдете на ней такую точку Е (Слайд 8), откуда можно одновременно покрыть для глаза булавкой b шест точки С, а булавкой a — точку А. Это будет означать, что вы отыскали на берегу третью вершину треугольника АСЕ, в котором угол С— прямой, а угол Е равен острому углу булавочного прибора, т.е.,  прямого. Очевидно, и угол А равен  прямого, отсюда АС = СЕ. Если вы измерите расстояние СЕ хотя бы шагами, вы узнаете расстояние АС, а, отняв ВС, которое легко измерить, определите искомую ширину реки.

2 способ.

Здесь также находят точку С на продолжении АВ и намечают при помощи булавочного прибора прямую СD под прямым углом к СА. Но дальше поступают иначе (Слайд 9).

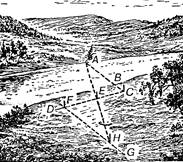
Слайд 9. Пользуемся признаками равенства треугольников.

Этот способ требует больше места, чем первый если местность позволяет осуществить оба приема полезно проверить один результат другим.

3 способ. (слайд10)

Описанный сейчас способ можно видоизменить. Отмерить на прямой СD не равные расстояния, а одно в несколько раз меньше другого.

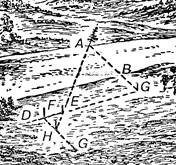
Слайд 10. Пользуемся признаками подобия треугольников.

Этот способ требует, как мы видим, меньше места и потому удобнее для выполнения, чем предыдущий.

Есть и другие способы измерения ширины реки, попробуйте дома найти их. Теперь нам предстоит задача более сложная».

Задача 4. Стоя у реки или озера, вы видите остров (Слайд 11).

Слайд 11

Нам захотелось измерить длину этого острова, не покидая берега. Можно ли выполнить такое измерение?

Хотя в этом случае для нас недоступны оба конца измеряемой линии, задача все же вполне разрешима, притом без сложных приборов.

Решение:

Пусть требуется узнать длину АВ (Слайд 12) острова, оставаясь во время измерения на берегу.

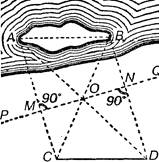
Слайд 12.

Избран на берегу две - произвольные точки Р и Q, втыкают в них вехи и отыскивают на прямой РQ точки М и N так чтобы направления АМ и BN составляли с направлением РQ прямые углы (для этого пользуемся булавочным прибором). В середине О расстояния МN втыкают веху и отыскивают на продолжение АМ такую точку С, откуда веха О кажется покрывающей точку В. Точно так же на продолжении ВN отыскивают точку D, откуда веха О кажется покрывающей конец А острова. Расстояние СD и будет искомой длиной острова.

4 Домашнее задание

Найдите где и как в окружающей Вас природе можно использовать геометрию

5 Итог урока. Рефлексия

Данный урок позволил научиться, осознано находить выход из не стандартной ситуации применяя математику.

Также этот урок способствовал качественному формированию таких мыслительных операций как анализ , сравнение, аналогия и т.д., а также формированию следующих качеств знаний учащихся: самостоятельность ума, глубина ума, осознанность, гибкость ума, устойчивость ума и др.