Конспект на тему "Угол между прямой и плоскостью" 10 класс

Конспект урока № 95

учителя математики Шимек Н.В

10 класс

дата проведения 27.12.2022г.

Тема урока: Угол между прямой и плоскостью.

Цели урока:

         Образовательная – введение нового понятия; отработка знаний, умений и навыков по

         нахождению угла между прямой и плоскостью; умение строить такие углы;

         Развивающая – умение распознавать угол между прямой и  плоскостью; развивать 

         практические навыки путем решения задач на нахождение угла между прямой и плоскостью;

         повышать уровень развития творческого мышления; развитие умения задавать вопрос;

          Воспитательная – слушать и слышать других учеников;  воспитывать вкус и интерес к

          геометрии; умение строить хороший  грамотный чертёж является важнейшим элементом

          геометрической культуры. 

Планируемые результаты:

          Предметные: знать понятия проекции фигуры на плоскость, угла между прямой и

          плоскостью; уметь решать задачи по теме.

Метапредметные:

Ø  коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений;

Ø  регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций;

Ø  познавательные: осуществлять сравнение и классификацию по заданным критериям.

          Личностные: формирование устойчивой мотивации к проблемно-поисковой деятельности.

Тип урока: урок открытия новых знаний

Оборудование:

Ход урока

1.       Организационный момент. Мотивация к учебной деятельности.

Приветствие, записать число, классная работа.

В геометрии, при работе с геометрическими фигурами, нас, прежде всего, интересует их взаимное расположение.

 На­вер­ня­ка вы слы­ша­ли такое вы­ра­же­ние: «Сол­неч­ный луч па­да­ет под углом…».

По сути, здесь идет речь об угле между пря­мой, ча­стью ко­то­рой яв­ля­ет­ся луч, и «плос­ко­стью» зем­ной по­верх­но­сти (хотя она, ко­неч­но, не со­всем плос­кая).

2.       Проверка домашнего задания.

Ученик заранее записывает решение задачи на доске и комментирует решение.

Другой учащийся у доски доказывает теорему о трёх перпендикулярах.

3.       Актуализация знаний учащихся.

·         Каким может быть взаимное расположение двух прямых в пространстве? (Прямые могут быть параллельны, пересекаться или скрещиваться).

·         .Каким может быть взаимное расположение прямой и плоскости в пространстве? (Прямая и плоскость могут пересекаться, быть параллельны или прямая может лежать в плоскости).

·         Если мы говорим о двух прямых, то одной из характеристик их взаимного расположения является угол между ними. Так, если прямые параллельны, то угол между ними считают равным 0°, если они перпендикулярны, то - 90°. А если прямые скрещиваются, то, как найти угол между ними? (Угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, параллельными им).

4.       Определение темы урока.

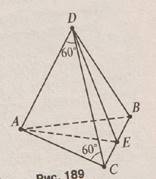Учитель на доске подготовил чертеж (рис.1)

Задание. Рассмотрите рисунок и ответьте на вопросы.

- Найдите ∠DAC.

- ∆ABC – равносторонний. Найдите ∠CAE.

- ∆BED –прямоугольный, ∠DEB=90, EB=BD. Найдите углы ∆BED.

- Найдите угол между прямой DE и плоскостью (АВС).

( Последний вопрос проблемный. Учитель и ученики формулируют тему и цель урока)

                                                                                                                                     рис.1

5.       Изучение нового материала.

   Определение 1. Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка,

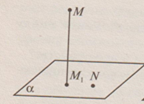если она лежит в плоскости.

      На рис.2 точка М₁ –проекция тоски М на плоскость ,

 а N-проекция самой точки N на ту же плоскость.                         рис.2

      Введем понятие проекции произвольной фигуры

 пространстве. Обозначим буквой  F какую-нибудь фигуру в

пространстве. Если мы построим проекции всех точек этой

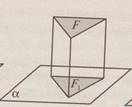фигуры на данную плоскость, то получим фигуру F₁ , которая называется проекцией фигуры F на данную плоскость. На рис.3

∆F₁ является проекцией ∆F на плоскость .                             

    Утверждение. Проекцией   прямой на плоскость, не                 рис.3                                                                                            перпендикулярной к этой прямой, является прямая.

   Задание. Сформулируйте определение угла между прямой и плоскостью, используя новые понятия.

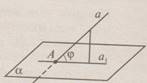    Определение 2. Углом между прямой и плоскостью,

 пересекающей эту прямую и не перпендикулярную к ней, называется угол между прямой и её проекцией на плоскость(рис.4)                    рис.4

     Обратите внимание, что угол между прямой и плоскостью – это

величина, а не фигура.

   - А если искомый угол между прямой и плоскостью будет задаваться прямой, перпендикулярной плоскости?

  - А если искомый угол между прямой и плоскостью будет задаваться прямой, параллельной  плоскости?

   Задание. Оформите эти два случая в виде таблицы.

6.       Первичное закрепление изученного материала

Задание (работа в папах). Решите задачу №165 (учебник)

                                                                            Дано:

                                                                                           А ∉, АО⊥О ∈ , АО=d,

                                                                                                       АВ=АС- наклонные, ∠АВО=∠АСО=30

                                                                                                      ∠ВОС=120

                                                                                        Найти: ВС

                                      Решение

1)       ∆ВАО=∆САО( по катету и острому углу, противолежащему катету).

ОВ=ОС.

Из ∆ВАО:  = tg 30, ОВ = d, ОС = d.

2)     В ВОС по теореме косинусов СВ² =ОВ² + ОС² – 2ОВОСcos120.

ВС²= 9 d² , ВС = 3d

 Ответ:      3d     

7.       Рефлексия учебной деятельности

(Ученики оценивают свою работу на уроке и качество усвоения материала, заполнив анкету.)

Вопросы анкеты

1.       Вспомни и запиши тему урока.

2.       Какие термины, факты, закономерности ты усвоил(а) на уроке?

3.       Считаешь ли ты полезными, интересными полученные знания?

4.       Какую оценку за урок ты бы себе поставил(а)?

(Учитель выставляет и комментирует отметки)

8.       Домашнее задание

- п. 21

- Разобрать решение задачи №162 (учебник)

- Решить задачу № 163