Уравнение, описывающее процессы в колебательном контуре

-Какие колебания называются гармоническими?

-Что такое электромагнитные колебания?

- Что такое колебательный контур?

- Свободные или вынужденные электромагнитные колебания в колебательном контуре? Почему?

- Какие процессы происходят в колебательном контуре?

-Чему равна энергия колебательного контура в любой момент времени?

Полная энергия колебательного контура, в любой момент времени, равна сумме энергий магнитного и электрического полей:  .

Электрический заряд, а значит и сила тока, при свободных колебаниях меняются с течением времени по закону косинуса или синуса, т. е. совершают гармонические колебания.

Колебания заряда описываются уравнением

q=q_mcosω_ot,

где q_m – амплитуда колебаний заряда (модуль наибольшего значения колеблющейся величины),

ω_o = - циклическая или круговая частота. Ее физический смысл – число колебаний за 2π с.

            Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание. Для гармонических колебаний Т=2π с (наименьший период косинуса).

Частота колебаний – число колебаний в единицу времени – определяется так: ν =  .

 Частоту свободных колебаний называют собственной частотой колебательной системы.  Так как ω_o= 2π ν=2π/Т, то Т= .

Циклическую частоту мы определили как ω_o = , значит для периода можно записать

Т=  = - формула Томсона для периода электромагнитных колебаний.

Тогда выражение для собственной частоты колебаний примет вид

.

            Так как , то колебания напряжения можно описать как U=U_mcosω_ot.

По определению ,  но q=q_mcosωt, поэтому

,

где π/2 – сдвиг фаз между силой тока и зарядом (напряжением). Итак, мы выяснили, что сила тока при электромагнитных колебаниях тоже меняется по гармоническому закону.

 (Посмотрим на рисунок 4.7 учебника, там вы видите графики зависимости заряда и напряжения на конденсаторе и силы тока в цепи от времени. На графиках хорошо видно, что сила тока сдвинута относительно заряда на π/2).

Мы рассматривали идеальный колебательный контур, в котором нет потерь энергии и свободные колебания могут продолжаться бесконечно долго за счет энергии, однажды полученной от внешнего источника. В реальном контуре часть энергии идет на нагревание соединительных проводов и нагревание катушки. Поэтому свободные колебания в колебательном контуре являются затухающими

Самостоятельная работа  Вариант 1

1.      Как изменится период колебаний в электрическом контуре, если емкость конденсатора увеличится в 2 раза, а индуктивность катушки уменьшится в 4 раза?

2.      Изменение электрического заряда конденсатора  в колебательном контуре происходит по закону q=0,2cos(πt/25). Чему равна частота колебаний заряда?

3.      Заряд на обкладках конденсатора колебательного контура меняется по закону q = 2 *10 ^-6 cos 10⁴ πt. Найдите амплитуду колебаний заряда, период и частоту колебаний, запишите уравнение зависимости тока в контуре от времени i = i (t).

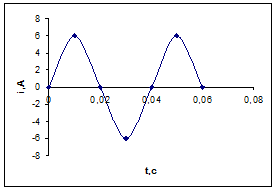
4.      По графику определите амплитудное значение силы тока, период и частоту. Напишите уравнение зависимости i = i (t).

Дома

§30, 31, 37,

Стр 109, упр 4, №1,2

Самостоятельная работа Вариант 2

1.      Как изменится частота колебаний в электрическом контуре, если емкость конденсатора в колебательном контуре увеличится в 2 раза, а индуктивность катушки уменьшится в 8 раз?

2.      Изменение электрического заряда конденсатора в колебательном контуре происходит по закону q = 0,2cos10⁴πt. Чему равен период колебаний заряда?

3.      Колебательный контур состоит из катушки индуктивностью 4 Гн и конденсатора электроемкостью 1 мкФ. Амплитуда колебаний заряда на обкладках конденсатора равна 100 мкКл. Напишите уравнение зависимости q = q (t)  и  i = i (t).

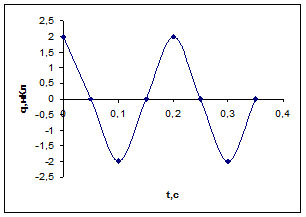
4.      По графику определите амплитудное значение заряда, период и частоту. Напишите уравнение зависимости q = q (t).