Конспект урока алгебры в 11 классе "Обобщение понятия степени""

Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них в них мысли.

А. Д. Александров

Цели урока: систематизировать и обобщить понятие степени с различным показателем;

отрабатывать умение применять указанные знания при решении задач; мотивировать на успешную сдачу экзамена;

формировать метапредметные связи.

Тип урока: обобщение и введение нового понятия.

Предварительная подготовка

Накануне урока выдать учащимся домашнее задание.

1.            Вы взяли кредит в банке 200 тыс. рублей под 13% годовых. Сколько

денег вы должны будете вернуть банку через год? Через два года?

2.            В банке взяли в кредит а рублей под р% годовых. Какую сумму нуж­но выплатить банку через год? Через два года? Через 5 лет?

Ход урока

Приветствие (1 мин.)

— Здравствуйте! Мы с вами написали две мониторинговые работы в рамках проекта «Я сдам ЕГЭ!» и многие из вас показали далеко не желаемые результаты. В экзаменационных работах обоих уровней обязательно встречаются задание на понятие степени и корня, и в них вы довольно часто делаете ошибки, или не знаете как их выполнять. Кроме того в экзаменационной работе профильного уровня задание № 17 предлагает задачу на так называемые сложные проценты, для которой можно составить формулы с использованием степени. Поэтому сегодня в качестве повторения материала и нам нужно будет   как-то осознать и обобщить понятие о показателе степени.  Но перед тем, как мы этим займемся, напишите небольшую диа­гностическую работу.

Актуализация знаний (5 мин.)

Диагностика: Проверить знание свойств степени с целым пока­зателем и свойства корней.

Вариант 1

Базовый уровень

1. Упростите: (ху²z ^–3)^{– 3}.

2. Вычислите:  .

Повышенный уровень

3. Упростите выражение

Высокий уровень

4. Вычислите:

Вариант 2

Базовый уровень

1. Упростите: (xy²z ^–3)².

2. Вычислите: .

Повышенный уровень

3. Упростите выражение

Высокий уровень

4. Вычислите:

 .

Проверка диагностики (1 мин.)

— Поменяйтесь друг с другом листочками. Про­верьте работу одноклассника по ответам. (Ответы проецируются на доску.)

У кого отметка «5»? У кого «4»? Есть те, кто не справился с работой? Сдайте листочки.

Введение понятия (7 мин.)

— А сейчас Вероника нам напомнит понятие степени с целым показателем и познакомит нас с решением домашней задачи.

— Мы с вами умеем вычислять степень числа с любым целочисленным показателем, руковод­ствуясь определением степени с целым показа­телем. А именно (определение степени дают учащиеся, учитель записывает их на доску.):

1) если п = 1, то а¹ = а;

2) если п = 0 и а ≠ 0, то а⁰ = 1;

3) если п = 2, 3, ... , то aⁿ = a · a · ... а;

                                                  п раз

4) если п = 1, 2, ... и а ≠ 0, то а ^{- n} = .

Как вы помните, понятие степени с натураль­ным показателем сформировалось еще у древних народов. Степени некоторых чисел использо­вались при решении отдельных задач учеными Древнего Египта и Вавилона. Но наиболее бур­ное развитие понятие степени получило с разви­тием банковского дела.

На дом вам была задана задача. В банке взяли в кредит а рублей под р% годовых. Какую сум­му нужно выплатить банку через год? Через два года? Через 5 лет?

Кто решил задачу? (Один из учащихся пишет формулу на доске.)

Через год банку нужно выплатить: a + a ·  

Через два года:  

И так далее.

— Хорошо. А если мы берем кредит не на целый год? Сколько мы должны вернуть, допустим, че­рез 3,5 года?

(Один из вариантов ответа учащихся: ис­пользовать степень с показателем 3,5.)

То есть мы видим, что решение этой проблемы привело к необходимости рассматривать не це­лый показатель степени.

— Скажите мне, пожалуйста, какая у нас сегод­ня будет тема урока?

(«Понятие степени с рациональным показа­телем».)

Что мы должны с вами вспомнить?

(Определение степени и ее свойства.)

О возникновении степени с рациональным показателем расскажет Кристина.

— Понятие степени с дробным положительным показателем ввел французский математик Оресли. Рассуждения его были примерно такими:

Рассмотрим, например, число . Существует ли оно? И что обозначает такая запись?

Допустим, что такое число существует. Хо­телось бы, чтобы и для этой степени с дробным показателем выполнялись известные нам свой­ства степени. Например, степень степени. Тогда будет верным следующее равенство:

            )⁵ = 4².

Обозначив  = а, получим равенство а⁵ = 4², откуда по определению корня получим:

 a     или  .

Mожете ли вы дать определение степени с ра­циональным показателем? Сформулируйте его (возможный ответ учащихся):

Степенью числа а с рациональным показате­лем, называется корень степени знаменателя из а в степени числителя. (Учитель записывает опре­деление на доске.)

Если   — обыкновенная дробь (q ≠ 1) и а ≥ 0, то под .

(Аналогично дается определение степени с отрицательным рациональным показателем.)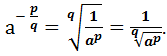

Первичное закрепление (14 мин.)

Фронтальная работа с классом (устно)

1. Представьте в виде степени или произведения степеней с дробными показателями:

а)                      б)                       в) 

г)                    д)                   е) 

ж)                 з)                    и^*)

2. Представьте в виде корня или произведения корней:

а)  ;                     б) ;                          в) ;

г)  ;   д*) ;             е*)  .

3. Вычислите (письменно, один ученик реша­ет первые два примера, второй — остальные):

a) ;             б)  ;             в) ;              г) .

Решение учащихся:

Работа в парах со взаимопроверкой

(Номера «а — г» можно решить несколькими способами — в зависимости от используемых свойств степени и корня.)

А теперь две минуты поработайте в парах. У вас на карточках два задания, выполнив зада­ния, проверьте друг друга.

Работа в парах с взаимопроверкой

1. Представьте в виде корня:

а)  ;                               б) .

2. Вычислите:

а);                  б) ;            в);            г) .

— А теперь, пользуясь определением степени рациональным показателем, решите уравнения (один ученик решает у доски):

  а)   = 1;  б)  = 4.

При решении первого уравнения обратите внимание на лишние корни, если таковые появятся.

Запись ученика на доске:  = 1, х² = 1³,  х = 1, х = – 1

Ответ: х = 1, х = – 1.

После ответа следует спросить у класса, где ошибка. Обратить внимание, что по определе­но степени с рациональным показателем х ≥ 0.

Динамическая пауза

Работа в группах (4 мин.)

Вспомните свойства степени с целым показателем.

(Учащиеся выписывают на доске свойства степени с целым показателем.)

     а^х · а^у = а^{х +у};        =а^{х – у};             (а^х)^у = а^ху.

Можем ли мы пользоваться этими свойствами и для степени с рациональным показателем?  

Закрепление материала (4 мин.)

Упростить выражение:

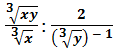а)               б);              в*). 

Дозированное домашнее задание (1 мин.)

В зависимости от своей оценки за диагностики, запишите себе домашнее задание.

Итоги урока

— В чём полезность сегодняшнего урока?

— На каком уровне вы оцениваете свои знания по данной теме?

Открытый урок

по алгебре и началам анализа

в 11 классе

подготовила и провела

учитель математики

МБОУ «СОШ № 2 ст. Архонская»

Уймина Т. А.

2016-2017 уч. год

Скачано с www.znanio.ru