
План-конспект урока по теме
Линейное уравнение с одной переменной
Тип урока: изучение и первичное закрепление нового материала
Цели:
Образовательные: организовать деятельность учащихся, направленную на изучение понятий: уравнение, линейное уравнение, корень уравнения, решить уравнение; закрепление умений тождественных преобразований; изучения алгоритма решения линейного уравнения с одной переменной.
Развивающие: создать условия для развития и обогащения словарного запаса, расширения кругозора, логического мышления и математической грамотной речи.
Воспитательные: содействовать воспитанию познавательной активности, ответственности, культуры общения и ведения диалога.
Методы и формы обучения: фронтальный, в парах, индивидуально;
«лови ошибку», игровой момент.
Оборудование: презентация Power Point, карточки с номерами, рабочий листок для каждого ученика, тесты, учебник, рабочая тетрадь.
План: (Структура урока)
I. Организационный этап
II. Проверка домашнего задания
III. Этап целеполагания
IV. Актуализация опорных знаний и способов действий
V. Изучение нового материала
VI. Физкультминутка
VII. Практическое применение полученных знаний
VIII. Подведение итогов урока. Рефлексия
IX. Информирование о домашнем задании
Ход урока
I. Организационный этап (1 мин)
1. Приветствие
2. Дальнейшие действия.
|
Учитель уточняет информацию об отсутствующих, делает записи в журнале. Знакомит учащихся с работой с оценочными листами: «Внимательно просмотрите оценочный лист. Запишите свою фамилию, имя, класс. Ознакомьтесь с содержанием первого столбца (вид деятельности) и второго (задание) – это какие виды работы вам предстоит выполнить на уроке. А в третьем столбце (баллы) – количество баллов, которые вы можете поставить себе за верный ответ. В конце урока, суммировав все баллы и используя приведенную ниже таблицу, вы сможете узнать свою отметку за наш урок». |
Учащиеся записывают в тетрадях дату и вид учебной деятельности: классная работа. Учащиеся слушают, при необходимости на них делают пометки |
II. Проверка домашнего задания (2 мин)
Проверка домашнего задания с использованием приема «Лови ошибку».
На слайде выполнены № 1-3 домашнего задания с заранее допущенными ошибками: на приведение подобных слагаемых, раскрытие скобок (Слайды 3 – 5)
В ходе проверки домашнего задания учащиеся отвечают на вопросы учителя:
1. Какие слагаемые называются подобными?
2. Как привести подобные слагаемые?
3. Сформулируйте правило раскрытия скобок, перед которыми стоит знак « + »
4. Сформулируйте правило раскрытия скобок, перед которыми стоит знак « - »
III. Этап целеполагания
- А сейчас, ребята, давайте определим тему нашего урока. Для этого вам необходимо разгадать ребусы (слайды 6-7)

- Тема нашего урока: «Линейные уравнения» (Учитель на доске записывает тему урока, учащиеся – в тетрадях)
- Какие цели мы перед собой поставим? (Совместно с учителем определяют цель и задачи урока)
Примерные ответы:
- к концу урока я буду знать термины и правильно применять понятия: линейное уравнение с одной переменной, корень уравнения, что значит решить уравнение;
- к концу урока буду уметь определять линейное уравнение по виду, определять его параметры.
(Слайд 8 – карта знаний. Наш урок – это путешествие. Рассмотреть карту.
В ходе выполнения заданий на каждой станции учащиеся получают жетоны с буквами )
IV. Актуализация опорных знаний и способов действий (слайд 9)
Бухта «теоретическая»
|
Действия учителя |
Действия учащихся |
|
1. Вводное слово учителя. Да, сегодня на уроке мы будем говорить об уравнениях. С ними вы встречались в начальной школе, а более подробно останавливались в пятом классе. |
Учащиеся слушают.
|
|
Приведите примеры уравнений и запишите их на доске и в тетради. |
Приводят примеры:
Делают записи в тетрадях, на доске. |
|
Внимательно посмотрите на свои записи и попробуйте дать определение понятию уравнения. |
Пробуют дать определение: Уравнение – это равенство, содержащее переменную. |
|
В приведенных вами уравнениях назовите неизвестные компоненты.
Давайте вспомним, как найти каждый из них.
Когда мы решаем уравнение, что мы находим? |
Слагаемое Множитель Делимое Делитель - Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. - Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. - Чтобы найти делимое, надо частное умножить на делитель. - Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Находим неизвестное, переменную, … . (Возможно, кто-то из учащихся вспомнит из курса 5-го класса, что при решении уравнения мы находим корень уравнения.) |
|
Попробуйте дать определение корня уравнения. Уточняет высказываний учащихся. А в уравнении 3х = 15, 5 –является его корнем? |
Корнем уравнения называется значение переменной, которое обращает это уравнение в верное числовое равенство. Да, 5 – корень данного уравнения. Так
как 15:3=5 или 3 |
|
Таким образом, напрашивается вопрос: «Что значит решить уравнение?» Дополнение учителя: «или доказать, что их нет». |
Решить уравнение – это значит найти все его корни. |
|
№ 1. Не решая уравнения, проверьте: какое из чисел является его корнем. Даны числа: 43, 13, 32 и 0 и уравнение 67 + (33 – х) = 68 (письменно в тетрадях)
(слайд 10) |
Если х = 43, то 67 + (33-43) = 68; 57=68 – неверно. Если х = 13, то 67 + (33-13) = 68; 87 = 68 – неверно. Если х = 32, то 67 + (33-32) = 68; 68 = 68 – верно Если х= 0, то 67 + (33 – 0) = 68; 100 = 68 - неверно. Ответ: 32 Вывод: число 32 – корень данного уравнения. |
|
В математике довольно часто встречаются уравнения, записи которых не имеют никакого сходства, но такие уравнения имеют одинаковые корни. Как они называются? На экране вы видите восемь уравнений, составьте пары равносильных, используя карточки с номерами. Обоснуйте свой ответ. 1) х+1 = 3 5) х-3=0 2) 2х - 7 =12 6) 5х = 0 3) (4+х) – 2 =2 7) х-3,5 = 2 4) -5х = - 6 8) 4х=8
(слайд 11) |
Уравнения, которые имеют одни и те же корни, называются равносильными.
(работа в группах) карточки Учащиеся поднимают карточки 1,8 (в одной руке) и 3,6 (в другой руке) Пары уравнений 1,8 и 3,6 являются равносильными. Так как корень уравнений 1 и 8 равен 2, корень уравнений 3 и 6 равен 0. Остальные уравнения общих корней не имеют, значит они не равносильны. |
|
Какими свойствами о равносильности уравнений мы используем при решении уравнений? |
При
решении уравнений используются свойства: |
V. Изучение нового материала (слайд 12)
Остров «Новых знаний»
|
Действия учителя |
Действия учащихся |
|
Многие процессы в жизни и природе можно описать уравнениями одного и того же вида:
которые можно записать следующим образом:
Найдите в учебнике определение линейного уравнения и зачитайте его. |
Слушают учителя.
Делают запись в тетради:
Зачитывают в учебнике на с. 28 определение линейного уравнения. |
|
В линейных уравнениях:
|
Учащиеся
называют значения параметров
|
|
Уравнения тоже являются линейными. |
|
|
Решение многих уравнений сводится к решению линейных уравнений. Рассмотрим пример: 5(11 – х) = 20 Ребята, как вы думаете, какие действия нам необходимо совершить, чтобы решить данное уравнение?
Обобщая ваши ответы, можно составить алгоритм решения линейных уравнений. (слайд 13)
У вас на столах лежит карточка-помощница. Еще раз мы повторим алгоритм решения уравнений. Посмотрите на нее внимательно. С левой стороны записан алгоритм решения уравнения и уже решено одно уравнение. А с правой стороны вам по аналогии нужно решить второе уравнение. |
Слушают учителя.
Учащиеся отвечают на поставленный вопрос.
Смотрят слайд.
Учащиеся выполняют задание в тетрадях. После выполнения – проверка. |
Карточка – помощница (слайд 14)
|
4(х – 11) – 2(5х – 7) = 0
1) Раскройте скобки: 4х – 44 – 10х + 14 = 0
2) Перенесите слагаемые, не содержащие переменную в правую часть, изменив при этом их знак на противоположный: 4х – 10х = 44 – 14
3) Приведите подобные слагаемые -6х = 30
4) Разделите обе части уравнения на коэффициент при переменной: х =30 : (-6) х = -5 |
2(3х + 7) – 8(х + 3)=0
1) Раскройте скобки: 6х + 14__________=__________
2) Перенесите слагаемые, не содержащие переменную в правую часть, изменив при этом их знак на противоположный: 6х - ____=__________
3) Приведите подобные слагаемые ______ = _________
4) Разделите обе части уравнения на коэффициент при переменной: х =_______ х = ______ |
VI. Физкультминутка
VII. Практическое применение полученных знаний (слайд 15)
Водопад уравнений
|
Действия учителя |
Действия учащихся |
|
На доске написаны три уравнения, решите их, пользуясь алгоритмом. Первая группа решает первое уравнение, вторая группа – второе, третья – третье. К доске выходят по 1 человеку из каждой группы.
1) 3(2х – 2) = 2(х + 5); 2) 2(3х – 3) = 3(2х -2); 3) 3(2х – 1) = 4(х + 2) + 2х;
Во все трех уравнениях были получены различные результаты. Таким образом, сколько корней может иметь уравнение? (слайд 15) |
К доске выходят трое учащихся и решают уравнения.
1) 3(2х – 2) = 2(х + 5); 6х – 6 = 2х + 10; 6х – 2х = 10 + 6; 4х = 16; х = 16 : 4; х = 4. Ответ: 4
2) 2(3х – 3) = 3(2х -2); 6х – 6 = 6х - 6; 6х – 6x = - 6 + 6; 0 · x = 0 верно при любом значении х. Ответ: бесчисленно много корней.
3) 3(2х – 1) = 4(х + 2) + 2х; 6х – 3 = 4х + 8 + 2х; 6х – 4x – 2х = 8 +3; 0 · x = 11 – неверно при любом значении х. Ответ: корней нет.
Один корень; бесконечно много корней и не иметь корней. |
Выполнение теста. (слайд 16) Тест
1) Равенство с переменной называется ….
2) Значение переменной, которое обращает уравнение в верное числовое равенство называется …
3) Укажите все уравнения, являющиеся линейными:
4) Укажите номера верных утверждений:
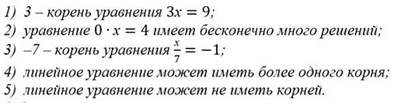
5) Корнем уравнения 5х = 40 является число:
6) Корнем уравнения -4х + 16 = 0 является число:
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
Остров сокровищ. (слайд 17)
Во время урока учащиеся собирали жетоны с буквами. В заключении необходимо собрать из них фразу: Молодцы! Так держать!
VIII. Подведение итогов урока. Рефлексия.
|
Действия учителя |
Действия учащихся |
|
Сегодня на уроке мы разобрали тему «Линейное уравнение». Чему вы научились, что нового узнали? И в заключении урока прошу ответить вас на вопросы в бланках: 1) На уроке я работал (активно/пассивно) 2) Своей работай на уроке я (доволен/не доволен) 3) Урок для меня показался (коротким/длинным) 4) За урок я (не устал/устал) 5) Мое настроение (стало лучше/стало хуже) 6) Материал урока мне был (понятен/не понятен) |
Ответы учащихся
Заполняют бланк «Рефлексия» |
I X. Информирование о домашнем задании (слайд 18)
П.7 выучить правила, №131(а,б), №132 (а)
Спасибо за урок!
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.