конспект урока на тему №Задачи на дроби"

Тема урока: Задачи на дроби. (1 урок)

Тип урока: Урок формирования знаний по теме «Задачи на дроби»

Цели урока:

дидактическая: продолжить формирование понятия обыкновенной дроби, познакомить учащихся с понятиями: целое, часть от целого, сформулировать правила нахождения части от целого и целого по его части, показать применение этих правил при решении задач; 

развивающая: развивать логическое мышление, умение анализировать, продолжить работу по развитию математической речи;

воспитательная: формировать эстетические навыки при оформлении записей, развивать навыки самоконтроля,  на примере  задач показать практическую значимость данной темы, формировать у учащихся самостоятельность мышления и интерес к изучению предмета.

План урока

1.     Оргмомент (определение темы и целей урока).

2.     Мотивация (из истории математики, связь с жизнью).

3.     Актуализация опорных знаний. Проверка д/з.

4.     Введение новых знаний.

5.     Решение задач.

6.     Подведение итогов.

7.     Домашнее задание.

Ход урока.

I.      Организационный:

Посмотрите, всё ль в порядке:

Книжка, ручки и тетрадки.

Прозвенел сейчас звонок.

Начинается урок.

Сообщение темы и цели урока: Сегодня на уроке мы продолжаем изучать обыкновенные дроби, рассмотрим основные виды задач на дроби, с которыми мы будем встречаться не только на уроках математики, но и в жизни.

(Записывают число и тему урока.)

II. Мотивация урока.

Есть у нас поговорка «попал в тупик», т.е. попал в такое положение, откуда нет выхода. У немцев аналогичная поговорка гласит, «попасть в дроби». Она означает, что человек, попавший в «дроби», попал в очень трудное положение.

Поговорка эта напоминает нам о тех временах, когда дроби считались самым трудным и самым запутанным отделом математики. Освоить же дроби было тяжело. Даже самые образованные люди считали действия с дробями весьма трудными. Это происходило потому, что общих приемов действия с дробями и записи дробей  не было.

Именно обыкновенные дроби помогут нам сегодня сделать очередное открытие в изучении математики.

III. Актуализация опорных знаний. Проверка д/з.

Повторение и систематизация знаний при выполнении устных упражнений:

Продолжите предложение:

1.      Обыкновенная дробь – это  

                                   (частное от деления натуральных чисел) 

                 m -      (это числитель дроби, делимое.)

                                  n -        (это знаменатель дроби, делитель.)

2. Знаменатель дроби показывает:

          (на сколько равных частей разделили единицу (целое))

Числитель дроби показывает:

                   (сколько таких частей взяли)

3. Определите, какая часть фигуры закрашена:

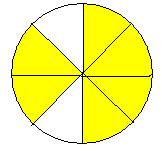
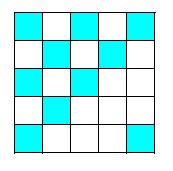
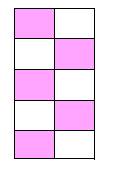
Учитель: Следит за верностью рассуждений. Задаёт вопросы.

Ученик: Отвечают  на вопросы,  после обсуждения   на экране высвечивается правильный ответ.

IV. Введение новых знаний.

1) Отыскание части от целого.

Задача.

Полный бочонок вмещает 1кг 400 граммов мёда. За обедом Винни–Пух съел  этого количества мёда. Сколько мёда съедено за обедом?

Учитель: Задаёт вопросы, следит за правильностью рассуждений.

1. Какая величина принята за целое? 

(1400 гр мёда)

2. На сколько частей поделили целое и как узнать какое количество мёда соответствует одной части?

(Целое поделили на 7 частей, одной части соответствует 200гр мёда)

3.Сколько таких частей взяли?

(взяли 5 частей)

Ученик: Читают задачу, отвечают на вопросы, после обсуждения решения записывают его в тетрадь. 1 ученик на доске записывает условие и решение.

Учитель: После ответа на вопросы на экране появляется графическая иллюстрация.

1400 : 7 = 200 (гр) – массы меда.

200 · 5 = 1000 (гр) – съел Винни–Пух за обедом.

Учитель: Сформулируйте правило: как найти часть от целого?

Ученик: Один ученик формулирует правило: нахождение части от целого.

Учитель: Хорошо, а теперь давайте прочитаем это правило в учебнике (стр 107)

Если часть целого выражена дробью, то чтобы найти эту часть, нужно целое разделить на знаменатель дроби и результат умножить на ее числитель.

2) Отыскание целого по его части.

Задача.

Буратино решил купить для папы Карло новый дом. 280 сольдо он уже накопил, это составляет  от всей стоимости дома. Какова полная стоимость дома?

Учитель: Задаёт вопросы, следит за правильностью рассуждений.

1.Какая величина принята за целое? Известна ли она?

(За целое приняли стоимость дома, эта величина  неизвестна)

2. На сколько частей поделили целое? Сколько таких частей взяли?

(Целое поделили на 9 частей, взяли 7 частей)

3.  Как узнать, сколько сольдо составляют одну часть?

(7 частей - это 280 сольдо, одна часть 280:7=40 сольдо)

Ученики: Предлагают и обсуждают решение задачи. Один ученик записывает решение на доске, остальные в тетрадь.

Учитель: Следит за грамотностью рассуждений. Совместно с учащимися выбирает метод решения, следит за грамотным решением у доски. После ответа на вопросы на экране появляется графическая иллюстрация.

                                           280 сольдо

                                           ? сольдо

280 : 7 = 40 (сольдо) – стоимости дома

40 · 9 = 360 (сольдо) – стоимость дома.

Учитель: Сформулируйте правило: как найти целое по его части?

Ученик: Один ученик формулирует правило: нахождение   целого по его части.

Учитель: Молодцы, а теперь давайте прочитаем это правило в учебнике (стр 108).

Если часть искомого целого выражена дробью, то чтобы найти это целое, нужно данную часть разделить на числитель дроби и результат умножить на ее знаменатель.

V. Решение задач.

Учитель: Мы познакомились с правилами решения задач на дроби, попробуйте применить эти правила при решении задач. Решаем совместно задачи №421 (2), №422 (2). Обязательно делаем схемы к этим задачам.

№ 421(2)

                                                32 музыканта

32 : 8 = 4 музыканта  часть оркестра

4 · 3 = 12 домбристов в оркестре.

№ 422 (2)

          48 вагонов

                 ? вагонов

48 : 3 = 16 вагонов – всех вагонов

16 · 4 = 64 вагона в депо.

VI. Подведение итогов.

Учитель: Давайте еще раз повторим правила на нахождение части от целого и целого по его части. Определите по схеме тип задачи и решите ее.

    1)     раздали

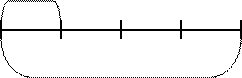                     24 конфеты

(отыскание части от целого. (24 : 4) · 1 = 6 конфет раздали)

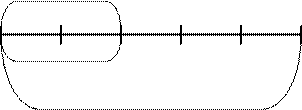2)       возраста брата

               10 лет

                                ? лет брату

(отыскание целого по его части. (10 : 2) · 5 = 25 (лет) брату)

Выполняя задания на уроке, вы показали умение самостоятельно мыслить, делать выводы, правильно оформлять решение задач и примеров.

VII. Домашнее задание.

№ 421 (3), № 422 (3).

Посмотрите в учебнике домашние задачи и задайте вопросы по их решению.