Поделиться
1-урок.pdf
Геометрия 9 класс урок №1
Определение тригонометрических функций углов от 0° до 180°
Цели:
Основная образовательная цель: организовать деятельность учащихся по изучению и закреплению знаний по теме «Тригонометрические функции угла от 0 до 180»: содействовать формированию оперировать понятиями синуса, косинуса, тангенса и котангенса угла от 0° до 180° и формированию умение находить тригонометрические функции тупых углов; выводить и применять формулы sin(180° - α) = sinα; cos(180° - α) = − cosα; 𝑡𝑔(180−𝑎) =−𝑡𝑔𝑎; с𝑡𝑔(180−𝑎)= −с𝑡𝑔𝑎.
Развивающие: содействовать развитию умению работать с чертежом, с формулами, с различными источниками информации.
Воспитательные: содействовать формированию мировоззренческих понятий; формирование у учащихся познавательного интереса к геометрии.
Ход уроков
Здравствуйте, ребята! Я рада приветствовать вас сегодня на нашем занятии.
- Начать наше занятие мне бы хотелось со слов известного физика Б. Паскаля: Величие человека - в его способности мыслить».
- Я очень надеюсь, что сегодня мы с вами будем мыслить, получать новые знания и успешно применять их на практике.
Сегодня мы продолжим изучение геометрии, но прежде чем приступить к изучению новой темы нам нужно вспомнить основные понятия, изученные в 8 классе, которые пригодятся нам на нашем сегодняшнем уроке.
Повторение ранее изученного материала.
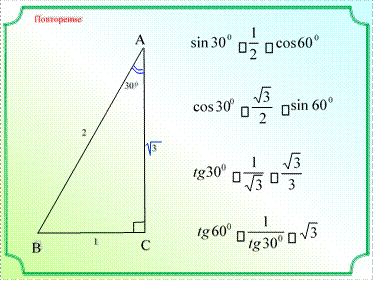
Что называют синусом острого угла прямоугольного треугольника?
Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Что называют косинусом острого угла прямоугольного треугольника?
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Что называют тангенсом острого угла прямоугольного треугольника?
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Что называют котангенсом острого угла прямоугольного треугольника?
Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.
УСТНО
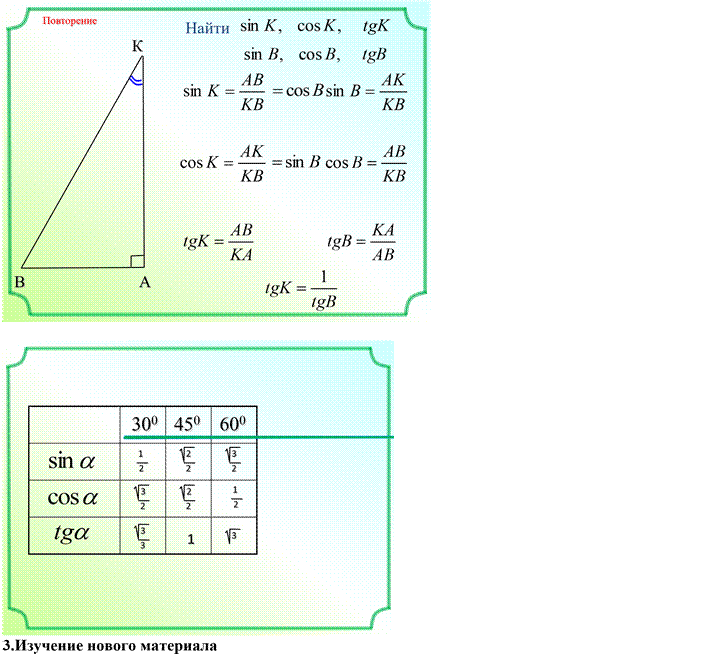
Мы вспомнили, что является синусом, косинусом и тангенсом угла в прямоугольном треугольнике. Теперь мы познакомимся с этими понятиями в независимости от фигуры, в которой они находятся.
Введем прямоугольную систему координат Оху и построим полуокружность радиуса 1 с центром в начале координат, расположенную в первом и втором квадрантах. Данная полуокружность называется единичной Запись в тетрадях:
Полуокружность называется единичной, если ее центр находится в начале координат, а радиус равен 1.
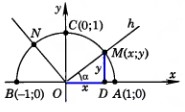
Из точки О проведем луч h , пересекающий единичную
полуокружность в точке М (х;у). обозначит буквой
угол между лучом h и положительной полуосью абсцисс. Если луч h совпадает с
положительной полуосью абсцисс, то будем считать, что = 0 . Если угол острый, то из
прямоугольного треугольника DOM имеем, sin
= 𝑀𝐷
, a cos
= 𝑂𝐷.
𝑂𝑀 𝑂𝑀
Но OM = 1, MD это ордината, OD - абсцисса, поэтому sin ордината у точки М, cos это абсцисса х точки М.
Запись на доске и в тетрадях:
Если угол
острый, то из прямоугольного треугольника DOM имеем, sin = 𝑀𝐷
, a cos
= 𝑂𝐷.
𝑂𝑀 𝑂𝑀
Но OM = 1, MD = y, OD = x, поэтому sin = y, cos = x. (1)
Так как из прямоугольного треугольника DOM тангенс - это
отношение противолежащего катета к прилежащему tg = у, то
тангенс будет равен отношению синуса угла
к косинусу угла
tg = 
sin. х cos
Существует еще функция, обратная тангенсу - катангенс, и он
равен отношению косинуса угла
к синусу ctg = cos .
sin
Итак, синус острого угла равен ординате у точки М, а косинус угла - абсциссе х точки М. Запишите в тетради (слайд 4).
Запись на доске и в тетрадях:
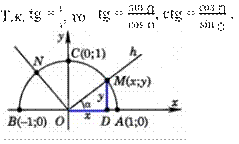
Учитель: если угол прямой, тупой или развернутый, это углы AOC, AON и AOB, или = 0 , то синус и косинус угла также определим по формулам (1).
Таким образом, для любого угла из промежутка 0 ≤ ≤ 180 синусом угла называется ордината у точки М, косинусом угла - абсцисса х точки М.
Так как координаты (х; у) точек единичной полуокружности заключены в промежутках 0 ≤ у ≤ 1, - 1 ≤ х ≤ 1, то для любого из промежутка 0 ≤ ≤ 180 справедливы неравенства: 0 ≤ sin ≤ 1, - 1≤ cos ≤ 1 (слайд 5). Запишите это в тетради.
Запись в тетрадях:
Т.к. 0 ≤ у ≤ 1, - 1 ≤ х ≤ 1, то для любого из промежутка 0 ≤ ≤ 180
0 ≤ sin ≤ 1, - 1≤ cos ≤ 1.
Учитель: а теперь найдем значения синуса и косинуса для углов 0, 90 и 180. Для этого рассмотрим лучи OA, OC и OB, соответствующие этим углам. Так как точки А, С и B имеют координаты
А (1; 0), С (0; 1), В (-1; 0), то
Sin 0 = 0, sin 90 = 1, sin 180 = 0, cos 0 = 1, cos 90 = 0, cos 180 = - 1. (2) Запишите в тетради.
Запись в тетрадях:
Sin 0
= 0, sin 90
= 1, sin 180
= 0, cos 0
= 1, cos 90
= 0, cos 180
= - 1 Учитель: так как tg = sin , то при
= 90 тангенс угла не определен,
так как cos 90
= 0 знаменатель cos
cos
обращается в нуль. Катангенс угла ctg = не определен при = 0 , = 180 , так как
знаменатель sin 0
sin
= 0, sin 180 = 0 обращается в нуль. Используя формулы (2), находим:
tg 0 = 0, tg 180 = 0. ctg 90 = 0.
Запишите это в тетради. (слайд 7) Запись в
тетрадях: Т.к. tg = sin , то при
= 90 тангенс угла не определен.
cos
tg 0 = 0, tg 180 = 0,
т.к. ctg = cos , то
при = 0 , = 180 катангенс
угла не
определен sin
ctg 90 = 0.
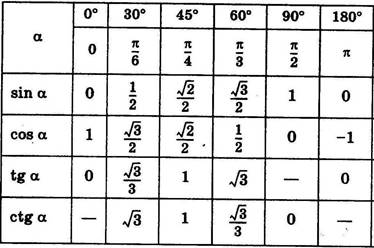
Учитель: кроме этих значений при решении задач вам понадобятся и другие значения синуса, косинуса, тангенса и катангенса при различных угла . Сделайте себе в тетради небольшую тригонометрическую таблицу значений синуса, косинуса, тангенса и катангенса (слайд 8). Запись в тетрадях:
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
