Конспект урока Отношение

 

Этап: Подготовительный

Цель: Актуализировать знания:  чисел; понятие делимое, делитель, частное, свойства деления; понятие процента

Актуализировать умения: распознавать различные виды числе;  переводить десятичные дроби в проценты; сокращать обыкновенные дроби

Метод: репродуктивный

Прием: репродуктивный, частично вопрос-ответ

Оборудование: проектор, доска, карточки

Учитель: Выполним задание на доске. Найдите число и определите его вид?

(на слайде №1 таблица с заданием)

2345	:	0	0,1	+	0,004	3	15
=	1,5	-	35		,	2,7

 

 Дети устно с места называют число и определяют его вид по очереди)

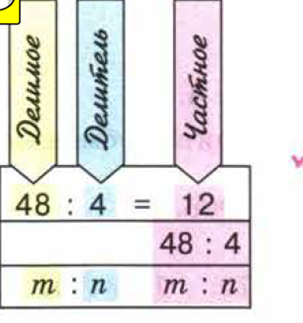
Учитель: А теперь вспомним, составляющие деления и что они обозначают (на вспомогательной доске изображена схема, с которой учитель знакомит детей). А также вспомним, что показывает делимое? К примеру, у Поли 3 шоколадки, а у Лены шесть, чтобы узнать во сколько раз шоколадок больше у лены, что нужно сделать?

Дети: нужно 6 разделить на 3, будет 2, что означает, что у Лены больше шоколадок в два раза.

 

 

Этап: Мотивационный

Цель: Возбуждение интереса к изучению понятия отношение

Метод: частично-поисковый

Прием: показ в практической деятельности

Оборудование: проектор

Учитель: (на слайде № 2 задача с текстом:

«В школе два 6-х класса: 6а и 6б, в каждом классе 2 и 20 учеников соответственно. После второй четверти в каждый класс было переведено по пять учеников с  соседней школы. Для какого из двух классов, размер класса значительно увеличился, несмотря на то, что в оба класса пришло одинаковое количество человек?»

   Решим задачу, условия которой расположены на доске. Можно высказать свой мнение без подтверждения математическими рассчетами?

Дети: для класса в котором 2 ученика приход пятерых значительно увеличил класс

Для класса, в котором 20 учеников, приход пятерых незначительно увеличил объем класса.

Учитель: Что вас привело к такому выводу?

Дети: мы сравнили количество учеников в двух классах.

Учитель: А как оформить при помощи математического языка данные утверждения и показать это при помощи конкретный вычислений, результаты которых нам позволят дать подобный вывод. Для этого нам нужно конкретизировать знания, полученные вами ранее и вывести новые из них.

 

Этап: Введение понятия – отношение в содержание обучения

Цель: Ввести определение понятия отношение

Метод: частично-поисковый

Прием:

Оборудование: две банки с водой, два картонных квадрата, две веревки

Подэтап: Введение понятия – отношение

 

Учитель: (на столе стоят две банки объемом 3 литра и 1 литр, доверху наполненные водой) Давайте сравним объем воды в трехлитровой банке с объемом воды в литровой банке. Что мы можем сказать про воду в первой трехлитровой банке?

Дети: в трехлитровой банке больше воды на 2 литра.

Учитель: а как еще можно сравнить используя свойство деления, которое мы с вами сегодня вспоминали.

Дети: 3разделить на 1 будет 3, что говорит, что в трехлитровой банке больше воды в три раза.

(на доске записываем результат сравнения 3:1=3)

 Учитель: (на столе две веревки длиной 2 и 5 дм.) Давайте сравним первую веревку длиной 2 дм. С веревкой, у которой длина 5 дм. Что мы можем сказать о первой веревке?

Дети: можно два разделить на 5 и получил 0,4, что говорит, что длина первой веревки в 0,4 дм. Больше длины второй веревки.

(на доске записываем результат сравнения 2:5=0,4)

Учитель: (на столе 2 квадрата разной площади) У первого квадрата площадь 4 кв.дм., у второго 1 кв. дм. Что мы можем сказать о площади первого квадрата в сравнении с площадью второго квадрата, опять же используя свойство деления?

Дети: 4делим на 1 будет 4, что говорит, что площадь первого квадрата больше площади второго квадрата в 4 раза.

(на доске записываем результат сравнения 4:1=4)

 

Учитель: (на слайде № 3 два отрезка, длиной 2 и 4 см)  Обратите внимание на два отрезка длиной 2 см. и 4 см. Что мы можем сказать о первом отрезке в сравнении его со вторым?

Дети: поделив 2 на 4 получим 0,5. Что говорит о том, что 2 больше 4 на 0,5

(на доске записываем результат сравнения 2:4=0,5)

Учитель: И последнее. Сейчас вы самостоятельно в тетрадях начертите два отрезка длиной 2 см. каждый. Что можно сказать о первом отрезке по сравнению со вторым используя свойство деления?

Дети: 2 разделить на 2 равно 1., что говорит, что первый отрезок больше второго в 1 раз.

(на доске записываем результат сравнения 2:2=1)

Учитель: Давайте постараемся выделить общее из полученных нами математических моделей. Что мы с вами делали в этих пяти задачах?

Дети: сравнивали.

Учитель: Мы сравнивали одноименные величины, то есть литры с литрами, дм. Длину с длиной, площадь с площадью, которые в свою очередь выражены конкретными числами. При помощи чего мы сравнивали?

Дети: при помощи деления.

Учитель: Что является результатом деления? А количество чисел, участвующих в сравнении?

Дети: Частное. 2 числа.

Учитель: какие закономерности можно выявить, при сравнении двух чисел при помощи деления если проанализировать сами числа, которые мы делили и результаты деления, то есть частное?

Дети: При делении большего числа на меньшее получается «целое» число, а при делении меньшего числа на большее, получается десятичная дробь.

Учитель: А если ответы сравнить с единицей?

Дети: в первом случае ответы больше единицы, а во втором случае, частное меньше единицы, а когда величины между собой равны, то в ответе получается единица.

Учитель: Итак, чтобы сравнить величины, мы  брали два числа, их характеризующие, делили одно на другое, результатом которого является частное. При этом если мы делили большее число на меньшее, частное было больше единицы, которое показывало, во сколько раз первое число больше второго и это можно представить в реальности, а когда мы делили меньшее на большее, частным было число, меньше единицы, и если мы вспомним две верёвки, что можно сказать, что частное показывает, какую часть первая веревка составляет от второй.

    Раз мы с вами сравнивали два числа, которые в результате сравнения вступали в определенную связь, в математике такую связь называют отношением. Обратимся к учебнику в котором имеется определение отношения и выделим существенные признаки, то есть те «маячки» которые характеризуют отношение.

Дети: - частное

           -2 чисел.

Учитель: а также обратим внимание на продолжение определения, в котором указывают на то, что показывает отношение. (Дети читают  определение)

И составим таблицу вариантов того, что может показывать отношение:

Дети: отношение показывает, во сколько раз первое число больше второго при условии, что первое число больше второго. Также отношение показывает, какую часть первое число составляет от второго, при условии, что первое число меньше второго.

Учитель: а есть ли третий вариант исходя из анализа ответов при делении?

Дети: когда частное равно 1, то 1 и 2 числа равны.

(на слайде постепенно появляются столбцы с таблицей копия которой раздается ученикам)

Результат деления	Частное <1	Частное >1	Частное =1
Что показывает отношение?	Какую часть первое число составляет от второго	Во сколько раз первое число больше второго	Оба числа равны
Делимое и делитель	Делимое < делителя	Делимое  > делителя	Делимое  = делителю

Подэтап: Формирование специальных математических действий – использование термина отношение в речи.  Интегрирован с подэтапом формирование специальных математических действий. Этап обучение применению понятия

Цель: сформировать умения правильно произносить отношения и осуществлять их запись.

Ориентировочная основа: Правило в учебнике(три варианта применения слово отношение).

Представление в материализованном виде: Учитель читает несколькими способами отношения, расположенные на слайде)

Слад№

Этап громкой речи:

Учитель: А теперь, каждый из вас вслух прочитает отношения на данном слайде.

Слайд №

 

 

      Дети по очереди читают отношение несколькими способами.

Подэтап: Формирование  специальных математических действий – умение записать отношение.

Цель: сформировать умение записать отношение в двух формах.

Ориентировочная основа:  прописывание на доске учителем двух форм записи отношения.

2 относится к 3
	2:3

 

Представление в материализованном виде:

Учитель: Давайте вспомним, на что мы можем заменить знак деления?

Дети: на дробную черту.

Учитель: в связи с чем любое отношение можно записать в двух формах:

2 относится к трем – 2:3 или  .

Этап громкой речи:

Учитель: А теперь каждый из Вас у доски запишет отношение в двух формах:

 

Подэтап: Формирование  специальных математических действий – умение находить значение отношения, или упрощать его.

Цель: сформировать умение находить значение отношения или производить его упрощение.

Ориентировочная основа:  решение учителем на доске  четырех примеров (ответ-целое число, ответ –десятичная дробь, ответ –обыкновенная дробь и случай с сокращением), а дети записывают указанные примеры в тетрадь

Представление в материализованном виде:  (Учитель решает четыре примера, на слайде №  написано задание : «вычислите отношения:

1)      25 к 5

2)        к

3)       0,4 к  

4)      4) 12 к 9)

Этап громкой речи:

Учитель: А теперь каждый из Вас у доски выполнит задание на слайде, а остальные будут производить эти же вычисления в своих тетрадях.

Слайд №

 

Этап внутренней речи: (оставшиеся два примера дети решают самостоятельно).

Учитель: Оставшиеся два примера прорешаем самостоятельно. Первый решивший, записывает ответы на доске.

Подэтап: Формирование  специальных математических действий – умение составлять отношение исходя из требований задачи.

Цель: сформировать умение составлять отношение исходя из требований задачи.

Ориентировочная основа: алгоритм составления отношения (во время проговаривания алгоритма, его пункты появляются на слайде №  , а после весь алгоритм на бумажном носителе раздается каждому ученику).

Тип: обобщенная

Учитель: Чтобы составить отношение, мы с вами воспользуемся информацией из таблицы, которую мы составили.

1)      Находим величины, которые нужно сравнить.

2)      Выясняем, выражены ли эти величины какими либо числами:

               1 путь                                 2 путь

              Если да?                            Если нет?

      Проверяем однородность     Находим интересующие нас величины

      единиц измерения                и следуем по первому пути.

3)      Выясняем, с каких слов начинается вопрос об этих величинах, которые нужно сравнить:

               «во сколько раз…?»                      «какую часть,..?»

           В числитель записываем              В числитель записываем

          большее число                                меньшее число

           а в знаменатель – меньшее           а в знаменатель – большее.

4)      Находим значение отношения.

Представление в материализованном виде: учитель реализует алгоритм на доске, решая две задачи, решение которых дети записывают в своей тетради.  ( На слайде №    указаны условия задачи.)

Задача № 1

Задача № 2

   Расстояние между поселками А и В составляет 2 км. Из поселка А в поселок В выехал велосипедист, который проехал 1200 метров.

   А) Во сколько раз пройденный велосипедистом путь превышает путь, который ему осталось проехать?

   Б) Какую часть всего пути составляет путь, который велосипедисту еще предстоит проехать до поселка В?

Задача № 3

Этап громкой речи:

Учитель: Решим задачу № 723 из учебника. ( к доске выходит ученик и решает задачу). Затем решает второй ученик задачу № 730 у доски.

   Этап внутренней речи:  дети самостоятельно решают задачи № 724, 728.

Подэтап: Формирование  специальных математических действий – умение пояснять, что показывает отношение.

Цель: сформировать умение пояснять, что именно показывает отношение.

Ориентировочная основа:  алгоритм.

Тип: обобщенная

   Учитель: чтобы пояснять, что конкретно показывает то или иное отношение, необходимо следовать алгоритму:

1.       Упрощаем отношение, то ест находим его значение

2.      Толкуем отношение, сравнив его с единицей  с опорой на теоретический материал из таблицы.

Представление в материализованном виде: учитель, ссылаясь на таблицу устно поясняет задачу, расположенную на слайде №    , акцентируя внимание на два варианта интерпретации, согласно таблице.

 

Слайд №

 

Этап громкой речи:

Учитель: выполним устно упражнение № 723 из учебника и на слайде

Слайд № 

   Кобра живет в среднем 15 лет, а крокодил, около 90 лет.

    Что показывают отношения:

1)15 к 90 ?     2) 90 к 15? .

Подэтап: Формирование  специальных математических действий – умение по заданному отношению воспроизвести ситуацию в реальности.

Цель: сформировать умение по заданному отношению воспроизвести ситуацию в реальности.

Ориентировочная основа:  алгоритм.

Тип: обобщенная

   Учитель: чтобы восстановить по заданному отношению ситуацию в реальности, необходимо следовать алгоритму:

1.       Сравнить значение отношения с единицей

2.      Толкуем размеры числителя и знаменателя, исходя из значения отношения  с опорой на теоретический материал из таблицы.

Представление в материализованном виде: учитель, ссылаясь на таблицу  поясняет упражнение, расположенную на слайде №    , акцентируя внимание на три варианта интерпретации,  согласно таблице, выполняет его на доске, показывая оформление, а дети производят соответствующие записи в тетрадях.

 

Слайд №

 

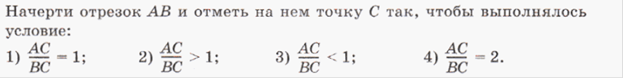
Этап громкой речи:

Учитель: выполним задания 1 и 2 на слайде № у доски и в тетрадях

 

Слайд № 

   Этап внутренней речи:  дети самостоятельно решают задачи 3 и 4 со слайда.

Учитель: А теперь вернемся к нашей первой задаче и попытаемся путем математических вычислений доказать, почему в один класс увеличился значительно, а второй нет? Итак, сколько было в 6а?

Дети: 20 учеников, стало 25. Если 25 разделить на 20, получится 1,25, что показывает во сколько раз увеличился 6а класс. В 6б было 2 стало 7, если 7 разделить на 2 то получится 3,5. Если мы сравним 1,25 и 3,5, то последнее число больше.

 

 

Домашняя работа

Средства: упражнения в учебнике № 751

Цель: Закрепление умений, полученных на уроке

Проверка: Будет проведена на следующем уроке

Инструктаж: Решить задания при помощи алгоритма составления отношения

Требования к выполнению: Решение полностью оформляется в тетради.

 

 

 

Подведение итогов урока:

Учитель: Что нового вы узнали на уроке?

Дети: Мы узнали как сравнивать числа при помощи составления отношения и толковать результат сравнения.

Оценивание учащихся, выходящих к доске:

На подготовительном и мотивационном этапе предполагается оценка ученика качественно отметкой, на остальных этапах количественной отметкой