
Предмет: Физика.
Класс: 9
Учитель: Елакова Галина Владимировна.
Место работы: Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №7» города Канаш Чувашской Республики.
Тема урока: «Гармонические колебания. Математический маятник».
Эпиграфом к нашему занятию будут следующие слова:
«Да, путь познания не гладок.
Но знаем мы со школьных лет:
Загадок больше, чем разгадок,
И поискам предела нет!»
Л. Татьяничева.
Цели: Организовать деятельность учащихся по изучению и первичному закреплению знаний учащихся по теме «Колебание», развивать способности к поиску решения проблемы, самостоятельному мышлению, умению формировать определения, стимулирование интереса к поиску фактов, событий; развитие коммуникативных способностей свободного и активного включения в диалог.
Планируемые результаты:
Основные понятия: Период, частота, математический маятник, число колебаний, гармоническое колебание, амплитуда, колебательная система, ускорение.
коммуникативные: формирование компетентностей в использовании ИКТ, умение организовать учебное сотрудничество, работать в группе, участвовать в коллективном обсуждении проблем, уважительно относиться к позиции другого, пытаться договариваться.
- регулятивные: умение организовать свою учебную деятельность: определять цель работы, ставить задачи, планировать, соотносить свои действия с планируемыми результатами.
-познавательные: умение работать с разными источниками информации, умения анализировать, объяснять, доказывать, защищать свои идеи, определять причины явлений
Личностные результаты: развитие навыков сотрудничества со сверстниками, формирование уважительного отношения к иному мнению.
Форма работы – групповая.
Организация образовательного пространства:
Межпредметные связи: физика, литература, биология, математика, история.
Мотивация к учебной деятельности.
Цель: включение в учебную деятельность на личностно значимом уровне
Деятельность учителя:
Вы узнаете:
- Какие колебания называются гармоническими?
-Что называется математическим маятником?
- При каких условиях реальный нитяной маятник будет совершать колебания, близкие
к гармоническим?
- Как меняются действующая на тело сила, его ускорение и скорость при совершении
им гармонических колебаний?
- Что является центростремительной силой при движении маятника?
- В чем заключается явление резонанса?
Вспомните:
-Что такое колебательное движение?
- Какие колебания называются свободными?
- Что такое колебательные системы?
- Что называется маятником?
- Что называется амплитудой колебания; периодом колебания; частотой колебания?
- Что такое одно полное колебание?
- Что называется маятником?
- Какая математическая зависимость существует между периодом и частотой колебания?
- Что называется собственной частотой колебательной системы?
- Какие колебания называются гармоническими?
Учитель: Мир колебаний! Он многообразен и всеобъемлющ. Сегодня мы с вами поговорим о самом загадочном явлении природы. Удивительны примеры колебательных систем в живой природе. Например: Сердце - одна из самых совершенных колебательных систем этого рода. Правильность работы сердца определяется синхронной работой целых групп мышц, обеспечивающих попеременное сокращение желудочков и предсердий. Синхронизацией этой работы «заведует» специальный орган, так называемый синусный узел, вырабатывающий с определенной частотой синхронизирующие импульсы электрического напряжения. Если синхронный режим сокращения мышц нарушается, то могут наступить так называемые фибрилляции – хаотические сокращения отдельных волокон сердечной мышцы, которые, если не принять экстренных мер, приводят к гибели организма. Поистине удивительно многообразие колебательных процессов в нашей Вселенной. Из-за колебаний листьев под действием ветра и трения их друг о друга возникают «звуки» леса (шелест). Это особенно заметно на листьях осины, так как они прикреплены к длинным и тонким черешкам, поэтому очень подвижны и раскачиваются даже самыми слабыми воздушными токами. Колеблются мосты, здания, вибрируют корпуса кораблей, самолетов, дрожат стекла в окнах, резонируя на звук проезжающего автомобиля, биение сердца, Останкинская башня, 52- метровая скульптура «Родина-мать» на Мамаевом кургане в Волгограде, автором которого является скульптор Е.В. Вучетич. Вершина 28-метрового меча даже при небольшом ветре раскачивалась с размахом до полуметра, что грозило разрушением великолепной структуры.
Ученик: В чем причина такой вибрации?
Учитель: Причиной вибрации являются срывы воздушных вихрей с поверхности меча. Строители пытались дополнительными мерами устранить вибрации, в титановой обшивке просверлили отверстия, внутри меча установили динамический гаситель колебаний. И хотя колебания уменьшились почти в полтора раза, меч решено было заменить, слишком много в нем было трещин. Новая форма изготовлена из малолегированной стали с плавными переходами в местах изменения толщины и ширины меча. Теперь амплитуда колебаний не превышает нескольких миллиметров, а за нормальным режимом эксплуатации следят датчики перемещений и напряжений.
Учитель: Нет возможности даже просто перечислить все известные волновые процессы. Сегодня мы попробуем научиться видеть поразительную схожесть всех колебательных процессов, называемых гармоническими, и определять на основе этой общности частоты колебаний интересующих нас систем. Для начала определим, что такое гармоническое колебание. Гармоническими являются колебания, которые происходят под действием силы, пропорциональной смещению колеблющейся точки и направленной противоположно этому смещению.
Периодическое изменение во времени физической величины, происходящие по закону синуса и косинуса, называются гармоническими.
Ученик: Иногда некоторые птицы во время далеких перелетов размещаются цепочкой или косяком. Одновременно ли птицы в цепочке взмахивают крыльями?
Учитель: Воздух обтекает тело вожака, как вода нос корабля. В пределах угла косяка уменьшается сопротивление воздуха. Взмахи крыльев косяка, кроме того, создают в воздушную энергию и облегчают движение более слабых птиц, т.е. птицы в косяке или цепочке связаны воздушной волной и работа их крыльев совершается в резонанс. Если воображаемой линией соединить концы крыльев птиц в определенный момент времени, то получается синусоида.
Ученик: В чем заключается явление резонанса?
Учитель: Амплитуда установившихся вынужденных колебаний достигает своего наибольшего значения при условии, что частота вынуждающей силы равна собственной частоте колебательной системы. В этом заключается явление, называемое резонансом.
Учитель: Если мы вывели способное колебаться тело из положения равновесия на небольшое расстояние х, и оно, стремясь вернуться назад, сопротивляется с силой F= - kx, то колебания тела, если его отпустить, называются гармоническими. Здесь k – жесткость системы, а сила kx вызывает у тела ускорение: а = - kx /m. Формулы Ньютона отлично действуют «на земле, в небесах и на море». Они сохраняют власть и под землей. Зная теорию тяготения, человек смотрит через планету, в глубь земных недр. И «глаз» для такого необыкновенного зрения самый простой из всех физических приборов – маятник. Можно поехать в Санкт Петербург и посетить Исаакиевский собор. Там ясно видно, что система отсчета, связанная с Землей, неинерциальна. ( youtube.com. Опыт Фуко)
Первая публичная демонстрация была осуществлена уже в марте 1851 года в парижском Пантеоне: под куполом Пантеона он подвесил металлический шар массой 28 кг с закреплённым на нём остриём на стальной проволоке длиной 67 м. Крепление маятника позволяло ему свободно колебаться во всех направлениях, под точкой крепления было сделано круговое ограждение диаметром 6 м, по краю ограждения была насыпана песчаная дорожка таким образом, чтобы маятник в своём движении мог при её пересечении прочерчивать на песке отметки. Чтобы избежать бокового толчка при пуске маятника, его отвели в сторону и привязали верёвкой, после чего верёвку пережгли. Период колебания маятника при такой длине подвеса составлял 16,4 секунды, при каждом колебании отклонение от предыдущего пересечения песчаной дорожки составляло около 3 мм, за час плоскость колебаний маятника поворачивалась более чем на 11° по часовой стрелке, то есть примерно за 32 часа совершала полный оборот и возвращалась в прежнее положение.
В далеком в 1851 году Леон Фуко сделал знаменитый эксперимент, который постоянно демонстрируется в Исаакиевском соборе. На протяжении нескольких минут этот опыт просто и наглядно доказал, что Земля вращается. На длинном (98 м) подвесе раскачивается массивный шар. В каждом качении он летит из края в край обширного помещения над полем, расчерченным четкими прямыми линиями. Маятник Фуко разгоняется земным тяготением, но благодаря инерции сохраняет плоскость своих колебаний. Земля же, медленно поворачиваясь, сдвигает из- под нее пол собора Летящий шар чуть-чуть сворачивает от прямых линий, начерченных на полу. Через две-три минуты накапливается заметное отклонение. Простейший вывод: Земля вертится. Система отсчета, связанная с земным шаром, неинерциальна.
Математический маятник — это материальная точка, подвешенная на невесомой и нерастяжимой нити, находящейся в поле тяжести Земли. Математический маятник — это идеализированная модель, правильно описывающая реальный маятник лишь при определенных условиях. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.
Ученик: А вот другая примечательная особенность маятника. Ее первым подметил Галилей. Тогда он был еще студентом. Посещал, как положено, богослужения в Пизанском соборе. И во время скучных месс развлекался разглядыванием массивных бронзовых люстр. Они были красивы, эти люстры, ибо сработаны самим Бенвенуто Челлини. Но особенно любопытно было наблюдать их мерные покачивания после того, как служитель, зажигавший свечи, ненароком толкал их своим длинным шестом. Во время богослужений, молитвенно обратив лицо к своду собора, можно было без помех наблюдать за качаниями люстр. И Галилео подметил: люстра качается, строго соблюдая ритм. Размахи происходят в одинаковое время. Правда, у Галилея не было часов, да и неловко было бы в соборе то и дело смотреть на часы. Все-таки он умудрился измерять время – по ударам своего пульса. Так Галилей сумел поставить физический опыт в церкви. Нашел и объект эксперимента, и измерительный прибор – собственное сердце.
Учитель: Открыв странную особенность маятника, он сразу же применил ее на пользу делу – устроил регистратор пульса, хороший инструмент для врачей. Это были по существу, первые маятниковые часы, которые теперь так много на нашей планете.
Ученик: Зачем нужен математический маятник и какое его применение на практике в жизни?
Учитель: В первую очередь ускорение математического маятника используется для геологоразведки, с его помощью ищут полезные ископаемые.
Ученик: Как это происходит?
Учитель: Дело в том, что ускорение свободного падения изменяется с географической широтой, так как плотность коры в разных местах нашей планеты далеко не одинакова и там, где залегают породы с большей плотностью, ускорение будет немножко больше. А значит, просто подсчитав количество колебаний маятника можно отыскать в недрах Земли руду или каменный уголь, так как они имеют большую плотность, нежели другие рыхлые горные породы. Также математическим маятником пользовались многие выдающиеся ученые прошлого, начиная с античности, в частности Архимед, Аристотель, Платон, Плутарх. Так Архимед и вовсе использовал математический маятник во всех своих вычислениях, а некоторые люди даже верили, что маятник может влиять на судьбы людей и пытались делать с его помощью предсказания будущего.
Учитель: Маятник, представляющий собой нить длиной l с точечным телом массой m на конце, отклонен на небольшой угол α.
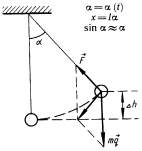
При этом,
возвращающая маятник в положение равновесия сила равна F
= mg tgα ≈ mg ![]() (при
малом угле отклонения). Полученное выражение для силы F
действительно имеет вид kx, при чем роль жесткости k играет величина mg/l. Поэтому все становится ясным: наши колебания –
гармонические. Период колебаний (время каждого полного размаха Т) зависит у
математического маятника (тяжелого тела, качающегося на легкой нити) только от
длины нити, точнее от - от квадратного корня длины. Масса же груза может быть
любой. Эту закономерность знал уже Галилей. А полную формулу вывел голландский
ученый Ганс Христиан Гюйгенс, последователь Галилея и современник Ньютона. Формула периода колебания математического маятника
впервые была открыта голландским ученым Гюйгенсом в далеком XVII веке. У маятника есть ряд интересных свойств, подтвержденных
физическими законами. Так период колебаний всякого маятника зависит от таких факторов,
как его размер, форма тела, расстояние между центром тяжести и точкой подвеса.
Поэтому определение периода маятника является не простой задачей. А вот период
математического маятника можно рассчитать точно по формуле, которая будет
приведена ниже. Т = 2π
(при
малом угле отклонения). Полученное выражение для силы F
действительно имеет вид kx, при чем роль жесткости k играет величина mg/l. Поэтому все становится ясным: наши колебания –
гармонические. Период колебаний (время каждого полного размаха Т) зависит у
математического маятника (тяжелого тела, качающегося на легкой нити) только от
длины нити, точнее от - от квадратного корня длины. Масса же груза может быть
любой. Эту закономерность знал уже Галилей. А полную формулу вывел голландский
ученый Ганс Христиан Гюйгенс, последователь Галилея и современник Ньютона. Формула периода колебания математического маятника
впервые была открыта голландским ученым Гюйгенсом в далеком XVII веке. У маятника есть ряд интересных свойств, подтвержденных
физическими законами. Так период колебаний всякого маятника зависит от таких факторов,
как его размер, форма тела, расстояние между центром тяжести и точкой подвеса.
Поэтому определение периода маятника является не простой задачей. А вот период
математического маятника можно рассчитать точно по формуле, которая будет
приведена ниже. Т = 2π![]() .
.
Ученик: Как доказать зависимость периода колебаний маятника от его длины и ускорения силы тяжести?
Учитель: При малых углах отклонения (а только при этих условиях
справедлива приводимая обычно формула маятника) дугу между шариками можно
заменить на хорду, где длина хорды равна S = 2‧l ‧ cos α. Движение маятника по этому пути можно рассматривать как
равноускоренное, так как проекция ![]() 1 силы тяжести
1 силы тяжести ![]() на направление движения маятника, т.е. вдоль хорды
равна
на направление движения маятника, т.е. вдоль хорды
равна ![]() 1=m
1=m![]() cosα.
Следовательно, модуль ускорения маятника составит
cosα.
Следовательно, модуль ускорения маятника составит ![]() =
= ![]() ‧cosα. При равноускоренном движении время, путь и ускорение
связаны зависимостью t =
‧cosα. При равноускоренном движении время, путь и ускорение
связаны зависимостью t = ![]() . Подставляя в последнее уравнение значение ускорения
при движении по хорде и длину этой хорды, а также учитывая, что период маятника
в четыре раза больше времени, необходимого для прохождения пути, получим для
искомой величины Т = 8‧
. Подставляя в последнее уравнение значение ускорения
при движении по хорде и длину этой хорды, а также учитывая, что период маятника
в четыре раза больше времени, необходимого для прохождения пути, получим для
искомой величины Т = 8‧ ![]() .
.
Ученик: Почему же в приводимой формуле перед квадратным корнем стоит коэффициент 2π?
Учитель: Вычисляя время движения маятника по хорде мы полагали ускорение в направлении движения все время постоянной и равным a = g‧cosα, где угол α соответствует наибольшему отклонению маятника от положения равновесия. На самом же деле его ускорение в направлении траектории является переменной величиной, достигающей максимума в моменты наибольшего отклонения и обращающейся в нуль при прохождении положения равновесия. Иначе говоря, ошибка состоит в незаконном использовании формул равнопеременного движения, тогда как в гармоническом колебательном движении скорость, время, путь и ускорение связаны гораздо более сложными зависимостями. В ходе наблюдений за маятниками были выведены следующие закономерности:
- Если к маятнику подвешивать разные грузы с разным весом, но при этом сохранять одинаковую длину маятника, то период его колебания будет одинаковым вне зависимости от массы груза.
- Если при запуске колебаний отклонить маятник на не очень большие, но все же разные углы, то он станет колебаться в одинаковым период, но по разным амплитудам.
Следовательно, период колебания у подобного маятника не зависит от амплитуды колебания, такое явление было названо изохронизмом, что с древнегреческого можно перевести как «хронос» – время, «изо» – равный, то есть «равновременный».
Гюйгенс был очень увлечен такими вот маятниками, увлечен настолько, что даже изобрел специальные часы с маятниковым механизмам, и часы эти были одними из самых точных для того времени.
Ученик: Есть ли такие примеры периодических процессов в биологии?
Учитель: Да. Многие цветы закрывают венчики с наступлением темноты; у большинства животных наблюдается годовая периодичность появления потомства; известно периодическое изменение интенсивности фотосинтеза у растений, колебание испытывают размеры ядер в клетках, численность животных определенного вида и т.д.
Ученик: Зачем понадобились «часы» живым организмам?
Учитель: Все живое существует в периодически меняющихся внешних условиях: день сменяется ночью, прилив отливом; чередуются времена года и т.д. Для наилучшего приспособления к их периодическим внешним условиям полезно иметь свои «часы», чтобы знать заранее, когда, например, наступит ночь, и успеть к этому приготовиться. Важная особенность колебательных систем – способность к взаимной синхронизации. Только благодаря этому живые «часы» могут настраиваться правильно, и из множества слабо связанных колебательных процессов возникает гармония периодического явления.

Маятниковые часы Гюйгенса.
Появление подобного изобретения сослужило большую пользу физике, особенно в сфере физических экспериментов, где точное измерение времени является весьма важным фактором.
Ученик: В формуле маятника под знаком квадратного корня в знаменателе стоит ускорение свободного падения. Почему?
Учитель: Ведь маятник, когда качается, падает. Правда, не свободно, но падает. А никакое падение не обходится без ускорения g. И здесь оно поэтому налицо. Причем из качения маятника его очень просто определить, и, что весьма приятно, без всякой спешки. Достаточно сделать маятник (маленький шарик на длинной нитке), измерить расстояние от точки подвеса до центра тяжести, чуть-чуть подтолкнуть его и сосчитать, сколько колебаний совершит он, скажем, за час.
Ученик: Что является центростремительной силой при движении маятника?
Учитель: Центростремительной силой при движении маятника является разность между натяжением нити и составляющей веса в направлении нити.
Ученик: Будут ли два полых шара иметь одинаковые периоды колебаний, если шары заполнены один водой, другой песком и подвешены на нитях одинаковой длины, отклонены на одинаковые углы?
Учитель: Да. Периоды колебания шаров будут одинаковы.
Ученик: Одинаково ли долго будут они колебаться в сосуде, из которого откачан воздух? Одинаково ли долго будут они колебаться в воздухе?
Учитель: В вакууме и в воздухе раньше остановится маятник с водой, так как часть энергии маятника будет израсходована на внутреннее трение слоев воды: кроме того, в начальный момент маятник с водой обладал меньшей потенциальной энергией, чем маятник с песком (плотность воды меньше плотности песка).
Ученик: В формуле маятника под знаком квадратного корня в знаменателе есть ускорение свободного падения. Это понятно. Ведь маятник, когда качается, падает. Правда, не свободно, но падает. Ускорение свободного падения на экваторе и на полюсе разные. Например, в Антарктиде действительные значения оказались чуть-чуть больше, чем теоретические. Больше! Что это могло означать? Раз большее значение g, значит, сильнее, чем «должно быть», поле тяжести. А поле тяжести увеличивается с приближением к центру масс Земли – так велит ньютоновский закон всемирного тяготения. Выходит, Антарктический материк погружен в земную кору глубже, чем, если бы он был неподвижен – ведь именно для неподвижного материка были вычислены теоретические значения g. Вывод: Антарктида не неподвижна. Она движется. А как – вверх или вниз, всплывает или тонет?
Учитель: Всплывает. Если бы Антарктида погружалась, она стремилась бы к уровню равновесия сверху и пребывала бы выше этого уровня, то есть дальше от центра Земли. Тогда поле тяжести на поверхности материка и, соответственно, значение g оказалось бы меньше, чем на уровне равновесия. Но истинное значение g вышло больше теоретического, вычисленного для уровня равновесия. Следовательно, Антарктида стремится к этому уровню снизу, находясь ниже его (ближе к центру Земли). Это и значит, что она всплывает. Ну, а всплывает то, что становится легче. Лед тает, масса его уменьшается.
Ученик: Как будут идти часы с секундным маятником, установленным для Москвы, на полюсе и на экваторе?
Учитель: На полюсе часы будут спешить, а на экваторе – отставать.
Ученик: Сохранится ли период колебаний часов-ходиков, если их перенести на Луну?
Учитель: Не сохранится. На Луне часы будут идти медленнее, чем на Земле.
Ученик: Как будет изменяться ход маятниковых часов при наступлении летних жарких дней по сравнению с холодными зимними днями, если часы установлены в неутепленном помещении (стержень маятника металлический)?
Учитель: Летом часы будут отставать. Период математического маятника зависит от ускорения свободного падения. Значит, часы, которые верно идут в Москве, будут идти вперед в С. Петербурге. Для того чтобы они шли верно, длину маятника нужно увеличить.
Ученик: Ж. Верн. «Дети капитана Гранта»: «- Как? – воскликнул Гленарван. – У акулы в желудке оказалась бутылка? – Самая настоящая, сэр, - ответил боцман».
Бутылка, плавающая в воде, будет колебаться, если ее легонько погрузить в воду и отпустить. Как определить частоту колебания бутылки?
Учитель: Пусть бутылка погрузилась на величину х, являющуюся отклонением бутылки от положения равновесия. При этом на бутылку начинает действовать дополнительная Архимедова сила, стремящаяся вернуть ее в положение равновесия и равная весу вытесненной воды:
F= ƍgSx, где g – ускорение
свободного падения; ƍ –плотность воды; S –поперечное сечение
бутылки. Роль жесткости системы «вода – бутылка» играет величина k = ƍgS.
При этом частота колебаний ⅴ = 1/Т =![]() ,
где 𝗆 – масса
бутылки.
,
где 𝗆 – масса
бутылки.
Ученик: Может ли пузырек в воде колебаться как маленькая упругая пружинка?
Учитель: Мы можем сделать вот что: давайте поищем претендентов на роль жесткости k и массе 𝗆 для пузырька, допустив, что колебания малы по амплитуде и поэтому, скорее всего, будут гармоническими.
Ученик: Почему пузырек, деформируясь в процессе колебаний, восстанавливает свою сферическую форму?
Учитель: Можно предположить, что здесь играет поверхностное натяжение. Кроме того, размерность коэффициента поверхностного натяжения Ϭ, на удивление, совпадает с размерностью коэффициента k (Н/м).
Ученик: А что взять в качестве массы? Масса воздуха в пузырьке?
Учитель: масса очень мала. Зато, колеблясь, пузырек расталкивает воду вокруг себя, и, двигаясь, вода обладает при этом запасом энергии. Поэтому ориентировочно возьмем в качестве 𝗆 массу воды, вытесненную пузырьком:
𝗆
= ƍ‧![]() ‧πR3
, где ƍ – плотность воды; R – радиус пузырька. Для частоты получим:
‧πR3
, где ƍ – плотность воды; R – радиус пузырька. Для частоты получим:
ⅴ = ![]() .
Пузырек может колебаться и не меняя своей сферической формы, а меняя лишь
объем. При этом роль k будет играть, видимо, давление. Для частоты при этом
получим: ⅴ =
.
Пузырек может колебаться и не меняя своей сферической формы, а меняя лишь
объем. При этом роль k будет играть, видимо, давление. Для частоты при этом
получим: ⅴ = ![]() .
Итак, пузырек воздуха в воде может совершать колебания двух типов.
.
Итак, пузырек воздуха в воде может совершать колебания двух типов.
Экспериментальная работа: «Исследование зависимости периода и частоты колебаний нитяного маятника от его длины».
Цель работы: Выяснить, как зависит период и частота свободных колебаний нитяного маятника от его длины.
Задание: 1 ряд: Длина нити 1= 1 м, число колебаний N =30.
2 ряд: Длина нити 1= 1 м, число колебаний N =30.
3 ряд: Длина нити 1= 1 м, число колебаний N =30.
Определить время t? Период Т? частоту ⅴ?
Измерения: 1 ряд: t=60с; T =t/ N = 2с; ⅴ=0,5 Гц.
2 ряд: t =42с; T = t/ N = 1,4с; ⅴ=0,7 Гц.
3 ряд: t =30с; T= t/ N =1с; ⅴ=1 Гц.
Можно
сделать вывод: с увеличением длины
маятника увеличивается период колебаний и уменьшается частота. Формула для
вычисления периода колебания математического маятника: ![]() ,
где
,
где ![]() –
длина маятника, g – ускорение свободного падения.
–
длина маятника, g – ускорение свободного падения.
Делаем вывод о том, что период будет пропорционален корню квадратному из длины маятника. Эту зависимость мы можем использовать в дальнейшем для анализа подобных колебаний:
![]()
Из
этого следует, что период мы можем записать как ![]() .
.
Другими
словами, если мы увеличиваем длину маятника в 4 раза, то период увеличится в 2
раза. Если увеличим длину маятника в 3 раза, то увеличится период в ![]() раз
и т. д. В этом и заключается результат экспериментальной работы.
раз
и т. д. В этом и заключается результат экспериментальной работы.
Задача: Какое значение получил для ускорения свободного падения учащийся при выполнении практической работы, если маятник длиной 80 см совершил за 3 мин 100 колебаний?
Ответ: 9,7 м/с2.
Задача: Коту Матроскину необходимо измерить площадь пола в коровнике. Как он может это сделать, имея часы с секундной стрелкой и кеды дяди Федора неизвестного размера на длинном шнурке?
Решение: Необходимо найти период колебаний кеда на шнурке с помощью часов:
Т = ![]() ,
где N – число колебаний, затем найти длину шнурка: Т
= 2 π
,
где N – число колебаний, затем найти длину шнурка: Т
= 2 π![]() ,
а затем l =
,
а затем l = ![]()
и измерить длину и ширину коровника шнурком и вычислить площадь.
Учитель: Я очень надеюсь, что урок прошел для вас с пользой и таинственный мир колебаний стал немного ближе и понятнее. Закончить урок мне бы хотелось словами Дмитрия Ивановича Менделеева: «Границ научному познанию и предсказанию предвидеть невозможно». Мы с вами только в начале большого пути познания природы и пусть впереди вас ждет мир удивительных открытий и свершений!
Рефлексия.
Впечатления и итоги занятия с помощью простой таблицы «Плюс, минус, интересно»:
1. «+» — все, что понравилось на уроке
2. «-» — все, что показалось бесполезным, скучным и не увлекательным
3. «Интересно» — что привлекло, заставило задуматься…
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
этот урок показался мне…
за урок я бы поставил себе, потому что…
мое настроение после задуматься…
Учитель подводит итоги.
Литература.
1. Перышкин А.В., Гутник Е.М.: Физика. 9 кл.: учебник для общеобразоват. учреждений/ А.В. Перышкин, Е.М. Гутник. –М.: Дрофа, 2019.
2. Анфилов Г. Б.: «Бегство от удивлений»; Издательство «Детская литература», Москва, 1967, с.288
3. Ковтун В.П.: «Занимательный мир физики». –СПб.: Дельта, 1997. - 240 с.
4. Тульчинский М.Е.: «Сборник качественных задач по физике»; Издательство «Просвещение», Москва, 1972, 235 с.
5. Усольцев А.П.: «Задачи по физике на основе литературных сюжетов. – Екатеринбург: У – Фактория, 2003. – 239 с.
6. Ланге В.Н.: «Физические парадоксы и софизмы»: Пособие для учащихся. -3-е изд., перераб. – М.: Просвещение, 1978. – 176 с.
6. youtube.com. Опыт Фуко.
7. Трембовольский Я.Л., Чекалов И.В.: «Ваше слово, эрудиты!»: Кн. для учителя: Из опыта работы. – М.: Просвещение, 1990. -144 с.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.