Конспект урока по геометрии в 9 классе "Метод координат"

Обобщающий урок по геометрии

 "Метод координат"

(9-й класс)

Цели урока:

·         систематизировать знания учащихся;

·         совершенствовать навыки решения задач методом координат;

·         подготовить учащихся к контрольной работе.

Оборудование:

·         интерактивная доска,

·         презентация “Метод координат на плоскости”.

Ход урока

1. Сообщение темы и цели урока.

Сообщается, что в ходе урока ученики будут набирать баллы и получат оценку в конце урока.

2. Вступительное слово учителя и сообщение учащегося из истории математики о Рене Декарте.

В это время на доске демонстрируется портрет ученого (слайд 2).

Текст сообщения (источник: Википедия):

Рене Декарт – французский математик, физик, физиолог и философ, создатель знаменитого метода координат, сторонник аналитического метода в математике, механизма в физике, предтеча рефлексологии.

Рене Декарт происходил из старинного дворянского рода. Его мать умерла от туберкулеза, когда ему исполнился 1 год. Отец Декарта был судьей и он мечтал видеть своего сына юристом. В возрасте 10 лет мальчик поступает в школу, а после ее окончания учится в Университете в Пуатье. Получив звание бакалавра и лицензию юриста , Рене выполнил желание отца, но в своей жизни он никогда не занимался юридической практикой. Он хочет видеть мир и открывать истину.

В истории математики Рене Декарт занимает видное место. Именно он сыграл решающую роль в становлении современной алгебры тем, что ввел буквенные символы, обозначил последними буквами латинского алфавита (х, у,z … ) переменные величины, а известные – первыми буквами латинского алфавит (а,b,c… ) ввел нынешнее обозначение степеней , заложил основы теории уравнений. Понятия числа и величины, ранее существовавшие раздельно, тем самым были объединены.

Историческое значение Декартовой геометрии состоит в том, что здесь была открыта связь величины и функции, что преобразовало математику. Применение алгебраических методов к геометрическим объектам, введение системы прямолинейных координат означало создание аналитической геометрии, объединяющей геометрические и арифметические величины, кото-рые со времен древнегреческой математики существовали в раздельности.

Физические исследования относятся главным образом к механике, оптике и строению Вселенной.

Крупнейшим открытием Декарта, ставшим фундаментальным для последующей психологии, можно считать понятие о рефлексе и рефлекторной деятельности.

Интересно, что великий русский физиолог Иван Павлов поставил памятник-бюст Декарту возле своей лаборатории, потому что считал Декарта предтечей своих исследований.

3. Повторение основных формул:

а) длина отрезка, координаты середины отрезка, координаты вектора, (с самопроверкой) – без ошибок -1 балл (слайд 3).

б) Какой вид имеет уравнение прямой? Рассматриваются частные случаи, уравнения осей координат (фронтально, слайд 4).

в) Взаимное расположение прямых на плоскости. Связь между коэффициентами (фронтально, слайд 5).

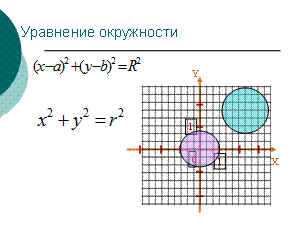
г) Уравнение окружности (фронтально, слайд 6).

4. Диктант с последующей самопроверкой ( слайд 7).

1. А(-5;1), В(-2;-3), АВ - ?

2. СД – диаметр окружности, С(4;-7), Д(2;-3). Найти координаты центра окружности,

3. Е(3;7). Принадлежит ли она графику уравнения ?

4. у = 4х-5 .Что является графиком уравнения?

5. Как расположены прямые х =3; у = -1?

5. Проверь себя (самопроверка по слайду 8 ) – с 1 ошибкой- 1 балл, без ошибок- 2 балла

6. Решение задач

В ходе решения задач идет накопление баллов учащимися. Тексты задач проецируются на доску, в ходе решения делаются необходимые краткие записи на интерактивной доске.

№1. Определить вид АВСD, если А(-2;2), B(4;-1), С(1;-7), D (-5;-4). ( слайд 9). Повторяются виды четырехугольников и их признаки. Учащиеся решают самостоятельно, затем решение проверяется (слайд 10)

№2.Определить вид треугольника АВС, найти его площадь, координаты центра и радиус описанной окружности, радиус вписанной окружности, если А(3;5), В(1;3),С(4;4).(слайд11)

№3.Лежат ли точки А(-1;3), B(1;-1), Е(0;1) на одной прямой? (слайд12)

№4. Является ли отрезок EF хордой окружности, если E(7;3), F(-1;1)? (слайд13)

№5.Написать уравнение прямой АВ, если А(-12;-7), B(15;2). Написать уравнение прямой: а) параллельной АВ; б) пересекающей АВ; в)перпендикулярной АВ.(слайд14)

№6. Дано: А(5;5), В(8;-3), С(-4;1). Найти координаты точки пересечения медиан треугольника АВС.(слайд15)

7. Итог урока.

Подсчет баллов, выставление оценок.

8. Задание на дом (слайд 16)

Повторить п.86-92, “3” №926а, 934а, 938а, 941.

“4-5” №993, 998, 1004, 1003*.

*Дополнительная задача (слайд 18).

Дано: А(6;1), В(-5;4), С(-2;5). Написать уравнение прямой, содержащей высоту, треугольника, проведенную к стороне ВС. (слайд18)

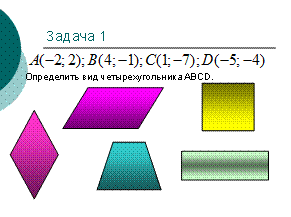
Скачано с www.znanio.ru