Конспект урока по информатике "Системы счисления"

Конспект урока информатики, 8-й класс. Тема: "Двоичная и десятичная системы счисления"

·         Магбудова Марьям Рагимовна, учитель информатики

Разделы: Информатика

Класс: 8

Цели урока: 

Образовательные:

• дать определение понятия «система счисления»;
• вывести алгоритм перевода чисел из двоичной системы в десятичную и наоборот;
• научится переводить числа из десятичной системы счисления в произвольную.

Воспитательные:

• воспитание информационной культуры, внимания, аккуратности, усидчивости.

Развивающие:

• развитие умения выделять главное (при составлении конспекта урока);
• развитие самоконтроля (анализ самоконтроля усвоения учебного материала по ведомости);
• развитие познавательных интересов (использование игровых приемов на уроке).

План урока: 

1. Организационный момент.
2. Объяснение нового материала и выполнение практической части урока.
3. Подведение итогов урока.
4. Домашнее задание.

Ход урока

1. Организационный момент.

Объявление темы и целей урока. Обозначение плана проведения урока.

Для того чтобы перейти к изучению десятичной и двоичной систем счисления, давайте разберемся что такое системы счисления и откуда они берут своё начало. Презентация «Системы счисления. Исторический очерк» (Приложение 1).

Начнем изучение темы сегодняшнего урока с одного, на первый взгляд, непонятного и запутанного стихотворения (Слайд 19 презентации).

Ей было тысяча сто лет,
Она в сто первый класс ходила,
В портфеле по сто книг носила – 
Все это правда, а не бред.
Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами, 
И десять загорелых рук
Портфель и поводок держали.
И десять темно-синих глаз 
Рассматривали мир привычно, 
Но станет все совсем обычным, 
Когда поймете наш рассказ.

Для того, чтобы разобраться, что же хотел нам сказать автор, нужно изучить тему «Двоичная и десятичная системы счисления». Итак, как вы уже догадались, тема сегодняшнего урока «Двоичная и десятичная системы счисления».

2. Объяснение нового материала и выполнение практической части урока.

Теоретический материал:

Система счисления – это принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса:

• позиционные – количественное значение каждой цифры зависит от ее место положения (позиции) в числе;
• непозиционные – цифры не меняют своего количественного значения при изменении их положения в числе.

Для записи чисел в различных системах счисления используется определенное количество знаков или цифр. Число таких знаков в позиционной системе счисления называется основанием системы счисления.

 развернуть таблицу

 развернуть таблицу

Каждое число в позиционной системе счисления можно представить в виде суммы произведений коэффициентов на степени основания системы счисления.

Например:

(степени расставляем над целой частью числа слева направо, начиная с «0»)

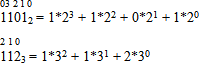
Теперь рассмотрим алгоритм перевода чисел из произвольной системы счисления в десятичную на примере.

Алгоритм перевода чисел из произвольной системы счисления в десятичную:

(степени расставляем над целой частью числа слева направо, над дробной частью – справа налево, начиная с «-1»)

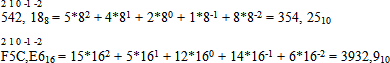
Двоичная система счисления имеет особую значимость в информатике. Это определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т. е. описываемым наборами только из двух знаков (0, 1).

Рассмотрим пример перевода числа из десятичной системы счисления в двоичную:

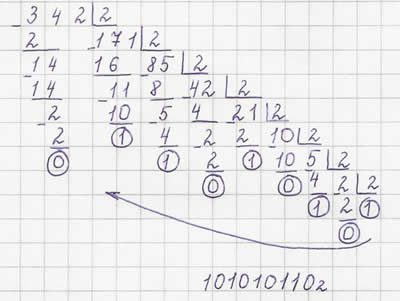
Рисунок 1

Пояснение: Решение оформляется на доске учителем с четким объяснение каждого своего действия.

Результатом является число, составленное из остатков от деления на 2 (которые мы обводили в кружок), записанное справа налево.

342₁₀ = 101010110₂

Теперь попробуйте записать рассмотренный алгоритм перевода числа из десятичной системы счисления словами(на выполнения задания отводится 2-3 мин., учитель контролирует его выполнение). По истечении отведенного времени учитель просит нескольких учеников прочитать составленный ими алгоритм. Затем остальные учащиеся под руководством учителя корректируют алгоритм. Учитель формулирует алгоритм, учащиеся записывают его в рабочие тетради.

Алгоритм перевода десятичных чисел в двоичную систему счисления: 

1. Разделить число на 2. Зафиксировать остаток (0 или 1) и частное.
2. Если частное не равно 0, то разделить его на 2, и так далее пока частное не станет равно 0. Если частное равно 0 , то записать все полученные остатки, начиная с первого, справа налево.

Теперь мы знаем, как переводить числа из десятичной системы счисления в двоичную и как переводить числа из произвольной системы счисления в десятичную. Решим несколько примеров (один ученик выходит к доске, остальные выполняют задание в тетради и сверяются с результатом на доске).

Задание:

1. Перевести в десятичную систему счисления числа: 101111001₂,1231₃, 110110101₂, 1223₃.
2. Перевести из десятичной системы счисления в двоичную, и наоборот числа: 256, 457, 845, 1073.
3. Записать алгоритм перевода числа из десятичной системы счисления в произвольную систему счисления.

Пояснение: задание выполняется у доски учащимися, которые назначаются учителем.

Для того, чтобы закрепить знания и умения, полученные сегодня на уроке, немного поиграем. Задание «постройте по точкам». Для выполнения этого задания вам понадобятся не только знания, полученные сегодня на уроке, но и математические знания.

Каждому ученику выдается тетрадный лист с нанесенной на нем системой координат (заранее подготавливается учителем) – Приложение 2.

Пояснение к заданию: каждая координата точки записана в двоичной системе координат. Вам надо перевести координаты точек в десятичную систему счисления и, применяя знания по математике, построить точки на системе координат, соединить их. Точки одного объекта обозначены одной буквой.

Голова:

• Г1 (101;1011)
• Г2 (1100;1011)
• Г3 (101;100)
• Г4 (1100;100)

Шея:

• Ш1 (111;100)
• Ш2 (1010;100)
• Ш3 (1010;11)
• Ш4 (111;11)

Глаза:

• Гл1 (110;1010)
• Гл2 (1000;1010)
• Гл3 (1000;1000)
• Гл4 (110;1000)
• Гл5 (1001;1010)
• Гл6 (1011;1010)
• Гл7 (1011;1000)
• Гл8 (1001;1000)

Нос:

• Н1 (1000;111)
• Н2 (1001;111)

Рот:

• Р1 (110;110)
• Р2 (110;101)
• Р3 (1011;101)
• Р4 (1011;110)

Антенки:

• А1 (110;1011)
• А2 (110;1111)
• А3 (101;1111)
• А4 (111;1111)
• А5 (1011;1011)
• А6 (1011;1111)
• А7 (1010;1111)
• А8 (1100;1111)

В итоге, у вас должен получится портрет хорошо знакомого вам РОБОТА.

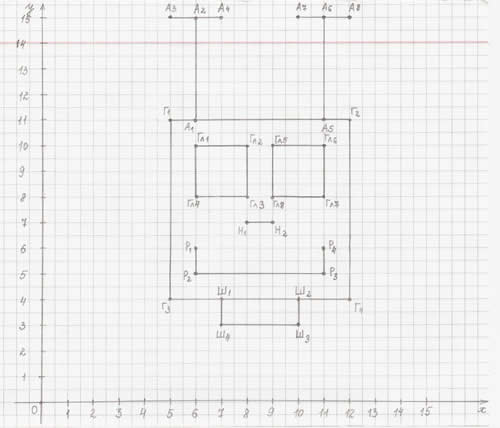
Рисунок 2

С образом робота учащиеся знакомы с 7-го класса: он является помощником, который помогает при выполнении практических работ и при изучении графического редактора Paint знакомились с создание рисунка методом аппликации и рисовали портрет робота.

3. Подведение итогов урока.

Учащиеся заполняют карточку Самоанализ усвоения учебного материала учащимся и сдают её учителю (Приложение 3).

Проверка выполнения задания («рисование по точкам»).

Фронтальный опрос:

• что такое система счисления;
• дайте определение понятию «основание системы счисления»;
• как перевести число из десятичной системы счисления в двоичную (алгоритм).

Выставление оценок за урок.

4. Домашнее задание.

Теперь вернемся к началу урока и вспомним стихотворение, которые нам было непонятно.

Примечание: Учитель раздает учащимся распечатку стихотворения (Приложение 4).

Домашнее задание: переформулируйте стихотворение, воспользовавшись знаниями, полученными на уроке.

Скачано с www.znanio.ru