Конспект урока по математике 6 класс "Координатная плоскость".

Декартова система координат на плоскости

Перечень рассматриваемых вопросов:

·         прямоугольная система координат;

·         координатная плоскость;

·         координатная ось, координата точки;

·         изображение точек с действительными координатами на плоскости.

Тезаурус

Координатная плоскость. Зададим на плоскости две оси координат, расположив их под прямым углом. Координатные оси пересекаются в точке, являющейся началом отсчёта для каждой из них.

Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.

Оси координат разделяют плоскость на 4 угла, которые называются координатными четвертями.

Координаты точки М (х; у), где х – абсцисса, у – ордината точки.

Обязательная литература:

1.   Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

1.   Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.

2.   Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Зададим на плоскости две оси координат, расположив их под прямым углом. Единичные отрезки осей возьмём равными друг другу.

Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.

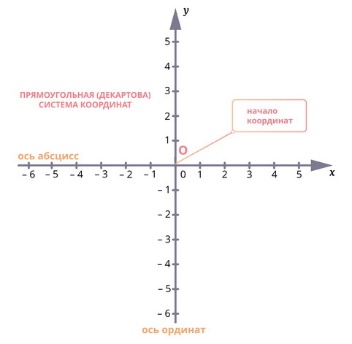
Положительное направление на осях указывается стрелкой.

Точку пересечения осей называют началом координат.

Оси взаимно перпендикулярны, поэтому заданную таким образом систему координат называют прямоугольной.

Оси координат разделяют плоскость на 4 угла – координатные четверти. Обозначают римскими цифрами как показано на рисунке.

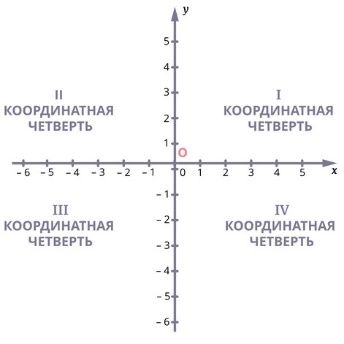
Одним из первых, кто начал широко использовать прямоугольную систему координат в своих исследованиях, был французский философ и математик Рене Декарт, поэтому её часто называют декартовой системой координат.

Пусть A – произвольная точка координатной плоскости. Проведём через точку A прямые, параллельные осям координат. Прямая, параллельная оси y, пересечёт ось x в точке A₁, а прямая, параллельная оси x, пересечёт ось y в точке A₂. Координату точки A₁ на оси x называют абсциссой точки A. Координату точки A₂ на оси y называют ординатой точки A. Абсциссу x и ординату y точки A называют координатами точки A.

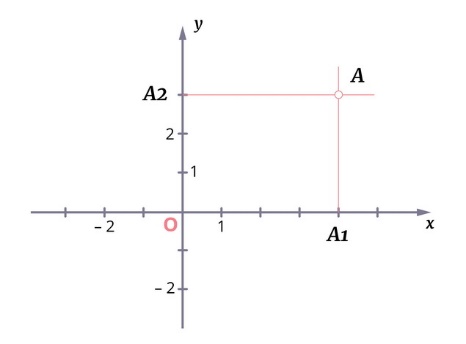
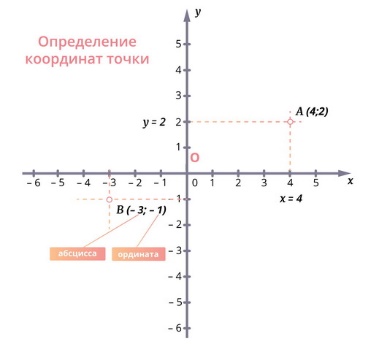
Координаты точки, записывают в круглых скобках рядом с буквой, обозначающей эту точку: М (х; у).

Важно!

х – первая координата

у – вторая координата

Поменять местами х и у нельзя – получится другая точка.

Поэтому пару координат (x; y) точки A называют упорядоченной парой чисел.

Если на плоскости задана прямоугольная система координат хOу, то:

– каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (координаты точки);

– разным точкам плоскости соответствуют разные упорядоченные пары чисел;

– каждая упорядоченная пара чисел соответствует одной точке плоскости.

То есть установлено взаимно однозначное соответствие между точками плоскости и упорядоченными парами чисел.

Алгоритм построения точки на координатной плоскости

Построим точку А(3; 6).

Введём прямоугольную систему координат.

На каждой оси откладываем заданные координаты х и у (x > 0 и y > 0, значит, точка A расположена в I координатной четверти).

Проводим перпендикуляры к оси х и оси у.

Точка их пересечения – искомая точка.

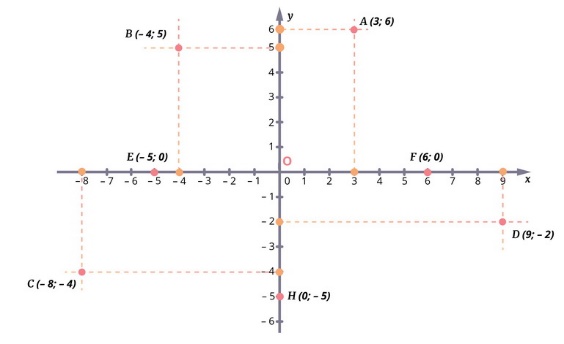
В(– 4; 5) – имеет отрицательную абсциссу и положительную ординату, значит, расположена во II четверти.

С(– 8; – 4) – имеет обе отрицательные координаты, значит, расположена в III четверти.

D(9; – 2) – имеет положительную абсциссу и отрицательную ординату, значит, расположена в IV четверти.

F(6; 0), E(– 5; 0) – точки лежат на оси абсцисс.

H(0; – 5) – точка лежит на оси ординат.

O(0; 0) – начальная точка системы координат.

В географии положение объектов на земной поверхности определяется двумя координатами: широтой и долготой.

В концертном зале своё кресло можно найти по номеру ряда и места.

В шахматах каждой клетке соответствует буква столбца и цифра ряда.

Разбор заданий тренировочного модуля

Тип 1. Ввод с клавиатуры пропущенных элементов в тексте

Построить прямую АВ, если А(3; 2), В(– 3; – 4).

Найти:

1) координаты точек пересечения прямой AB с осями;

2) координаты середины отрезка AB.

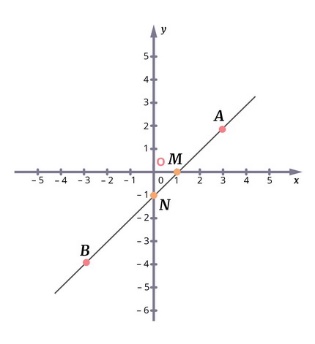
Шаг 1. Строим точки А и В по их координатам.

Шаг 2. Проводим прямую АВ.

Шаг 3. Находим точки пересечения с осями координат, обозначаем их буквами M и N. Определяем их координаты:

М (1; 0), N (0; – 1).

Шаг 4. Находим по графику середину отрезка АВ, это точка N (0; – 1).

Ответ: координаты точек пересечения прямой AB с осями: М (1; 0), N (0; – 1), координаты середины отрезка AB: N (0; – 1).

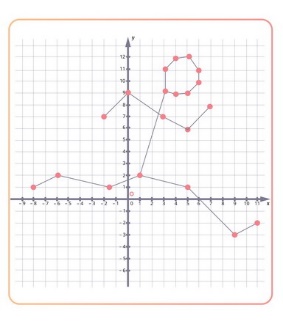
Тип 2. Нарисуйте фигуру, последовательно соединяя точки

(0; 4), (– 2; – 2), (3; 2), (– 3; 2), (2; – 4), (0; 4).