Исследование показательных и логарифмических функций

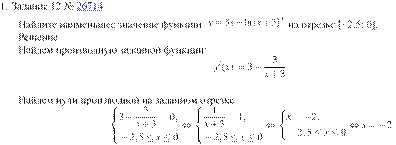
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

В точке  заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

Ответ: −6.

1/15

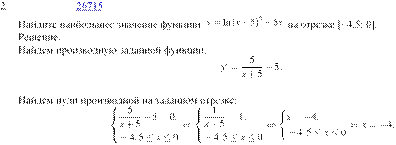
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

В точке  заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:

Ответ: 20.

3. Задание 12 № 26716

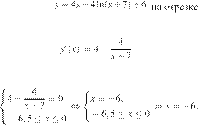Найдите наименьшее значение функции           Решение.

Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

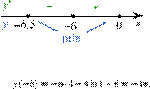В точке  заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

Ответ: −18.

2/15

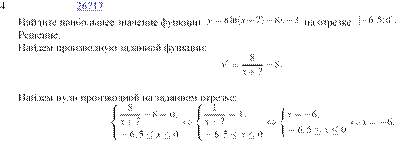
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

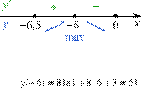В точке  заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:

Ответ: 51.

3/15

5.                      26718

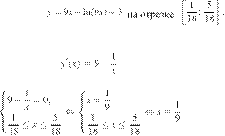Найдите наименьшее значение функции

Решение.

Функция определена и дифференцируема на заданном отрезке. Найдем ее производную:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке, и изобразим на рисунке поведение функции:

В точке  заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

Ответ: 4.

4/15

6.                      26719

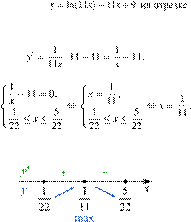      Найдите наибольшее значение функции                                                  

Решение.

Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

В точке  заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:

Ответ: 8.

5/15

7.                      26720

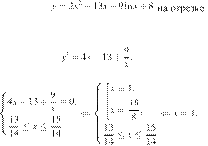      Найдите наибольшее значение функции                                                       

Решение.

Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

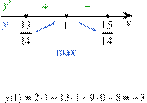В точке  заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:

Ответ: −3.

6/15

8.                                  26721

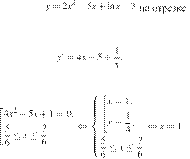      Найдите наименьшее значение функции                                                   

Решение.

Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

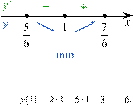В точке  заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

Ответ: −6.

9.                                  Задание 12 № 26722

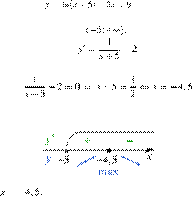Найдите точку максимума функции Решение.

      Функция определена и дифференцируема на                 Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Ответ: −4,5.

7/15

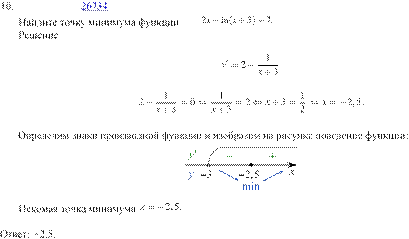Найдем производную заданной функции:

Найдем нули производной:

11. Задание 12 № 77486

Решение.

Заметим, что      Область определения функции — открытый луч  Найдем производную заданной функции:

Найдем нули производной:

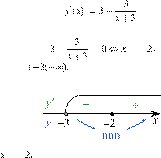Найденная точка лежит на луче         Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума

Ответ: −2.

8/15

12.                                   77487

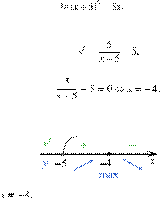Найдите точку максимума функции Решение.

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Ответ: −4.

13.                                   Задание 12 № 77488

Решение.

Заметим, что      Область определения функции — открытый луч  Найдем производную заданной функции:

Найдем нули производной:

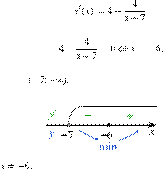Найденная точка лежит на луче         Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума

Ответ: −6.

9/15

14.                       77489

Решение.

      Заметим, что                                    Область определения функции — открытый луч

Найдем производную заданной функции:

Найдем нули производной:

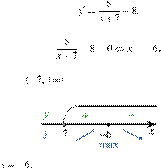Найденная точка лежит на луче         Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Ответ: −6.

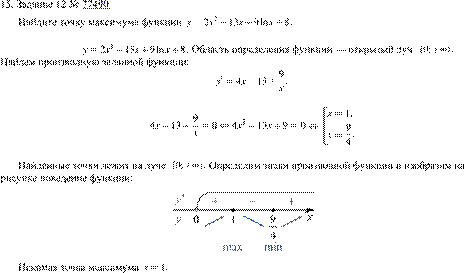Решение.

Заметим, что

Найдем нули производной:

Ответ: 1.

10/15

Найдем производную заданной функции:

Найдем нули производной:

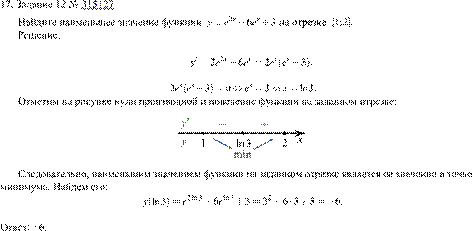Найдем производную заданной функции:

Найдем нули производной:

11/15

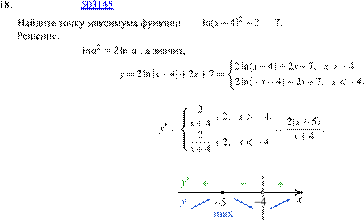Заметим, что

Тогда

Производная обращается в нуль в точке −5, которая является точкой максимума.

Ответ: −5.

Приведём другой способ нахождения производной

12/15

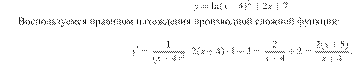
Найдем нули производной:

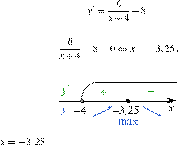Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Ответ: −3,25.

20. Задание 12 № 510847

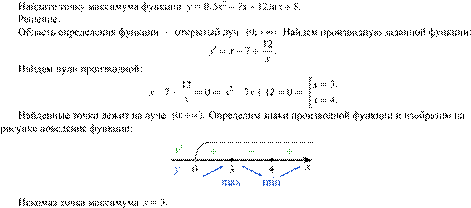
Ответ: 3.

13/15

21.                                   510943

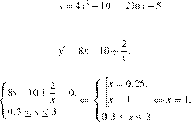      Найдите наименьшее значение функции                                     на отрезке [0,3; 3].

Решение.

Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

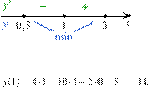В точке  заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

Ответ: −11.

22.                                   Задание 12 № 526012

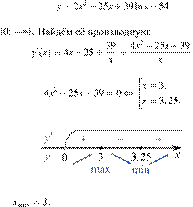Найдите точку максимума функции Решение.

Функция определена на

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Ответ: 3.

14/15

Ключ

15/15