Конспект урока по теме : «Основные формулы для sin α и cos α.»

Открытый урок по теме:

«Основные формулы для sin α и cos α.»

10 класс

( конспект урока)

Выполнила: Шестиалтыннова М.В.,

учитель математики,

                                                               Югорск

2023

Конспект урока

Открытый урок по теме «Основные формулы для sin α и cos α.», 

10 а класс (базовый уровень).                                           

Дата проведения:  19.04.2023.

(Программа Фестиваля  «Открываем двери детского сада ,школы»)

Цели урока:

Образовательные: обобщить и систематизировать знания учащихся по теме; продолжить формирование умений и навыков по применению тригонометрических формул; проконтролировать степень усвоения знаний, умений и навыков по теме;

Развивающие:  совершенствовать, развивать умения и навыки по решению задач на применение тригонометрических формул; тригонометрического круга;

Воспитательные:  воспитывать трудолюбие; стимулировать мотивацию и интерес к изучению тригонометрии;

Задачи урока: повторить определение синуса, косинуса; повторить основное тригонометрическое тождество и формулы; научить применять полученные знания при решении задач;

Тип урока: урок обобщения и систематизации знаний;

Методы обучения:  частично-поисковый,  тестовая проверка уровня знаний, организация и осуществление мыслительной деятельности, проблемно-поисковый, практический, проблемный.

Оборудование: учебник по алгебре и начала анализа, раздаточный материал, компьютер, доска, мел.

Ход урока

1.Организационный момент: приветствие, проверка готовности к уроку. Учитель объявляет тему урока,  цели урока,  план урока

План урока:

1.                  Организационный момент, вступительная беседа (3 мин);

2.                  Блиц-опрос (6-7 мин с проверкой);

3.                  Закрепление  знаний и умений (15 мин)

4.                  Физкультминутка (гимнастика для глаз) (1 мин)

5.                  Самостоятельная работа (тест с проверкой, 10 мин)

6.                  Историческая справка : «Это интересно» (3 мин)

7.                  Подведение итогов урока (2 мин)

8.                  Домашнее задание (1мин)

      Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sin, cos, соотношение sin²+ cos²=1 .  Каждый раз выводить нужную формулу, например, для преобразования тригонометрического уравнения время уйдет достаточно много. Поэтому круг формул, которые необходимо знать, должен быть достаточно широким.

Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. “Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” писал Г. Спесер, английский философ и социолог.

Так вот, давайте сегодня на уроке работать активно, внимательно, будем поглощать знания с большим желанием, ведь они вам пригодятся. Для чего нужны хорошие знания? Как вы думаете? Дети отвечают на поставленный вопрос? Учитель обобщает ответ: «Знания- это великая сила, дающая нам уверенность в будущем!». Учитель предлагает парную работу.( Свою пару надо найти с помощью формул перевода из градусов  в радианы и наоборот)

2.  Актуализация опорных знаний (6-7 мин)

Блиц-опрос на работу с единичной окружностью (самоконтроль)

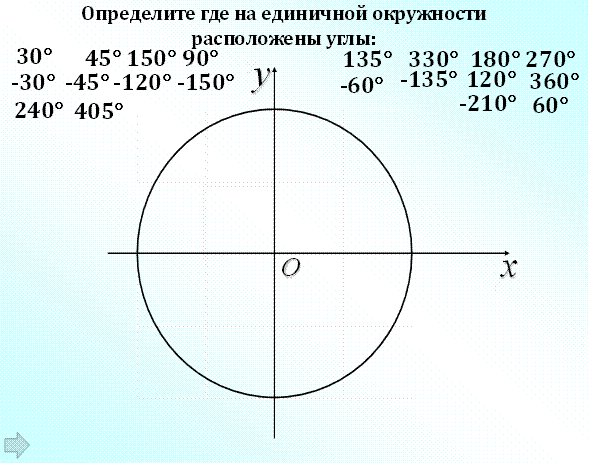
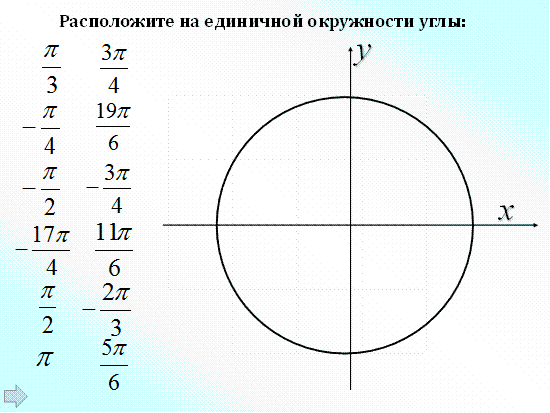
Критерии оценивания:

Проверка проводится на уроке с выставлением оценок. Все выполнены задания правильно – «5»; 1-3 ошибки-«4»  4-6 ошибок—«3»; более 6—«2».

3. Закрепление знаний и умений: работа с учебником (желающие идут к доске)

4.Физкультминутка (1 мин)

5. Самостоятельная работа обучающего характера в форме теста, с последующей проверкой на уроке (взаимопроверка)

Ответы: 1 вариант: 1 (б); 2(в); 3(а)

              2 вариант: 1 (а); 2(б); 3(б)

6. Историческая справка. Беседу проводит ученица 10 а класса Лихушина Майя  по теме «История зарождения тригонометрии».

       Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц.

Тригонометрия в ладони

      Значения синусов и косинусов углов “находятся” на вашей ладони. Протяните руку и разведите как можно сильнее пальцы, так как показано на слайде. Сейчас мы измерим углы между вашими пальцами. (Возьмем два прямоугольных треугольника с углами 30°и 45° и приложим вершину нужного угла к бугру Луны на ладони. Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону угла совмещаем с мизинцем, а другую сторону - с одним из остальных пальцев)

Смотрите, я прикладываю угол в 30°; оказывается, это угол

- между мизинцем и безымянным пальцем;

- между мизинцем и средним пальцем - 45°;

- между мизинцем и указательным пальцем - 60°;

- между мизинцем и большим пальцем - 90°;

И это у всех людей без исключения.

Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить (сжать) пальцы с мизинцем, угол между лучами будет равен 0°, то есть можно считать, что направление мизинца соответствует началу отсчета углов, то есть 0°, а поэтому введем нумерацию пальцев:

№0 - Мизинец

№1 - Безымянный

№2 - Средний

№3 -Указательный

№4 - Большой

Значения синуса и косинуса угла по “ладони” приведено в таблице.

Примечание. Для определения косинуса угла отсчет пальцев происходит от большого пальца руки.

7. Подведем итог урока:

Мы пополнили словарный запас математического языка следующими терминами: основное тригонометрическое тождество, область значений синуса и косинуса, четность и нечетность,

мы получили соотношения для синуса и косинуса одного и того же угла. Научились находить значение синуса или косинуса, используя основное тригонометрическое тождество; занимались преобразованием тригонометрических выражений.

Объявляются оценки за урок.

Домашнее задание: Учебник открыть на стр. 214, № 7.55, № 7.56.

Посмотрели номера, есть вопросы по заданиям.

Спасибо, урок окончен!  До свидания.

Литература:

1.Алгебра и начала анализа. 10 класс: Учебник для общеобразовательных учреждений/С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – 6-е изд. – М.: Просвещение, 2019.
2. Алгебра и начала анализа. Дидактические материалы для 10 класса/ М.К. Потапов, А.В. Шевкин. – М.:Просвещение, 2019.
3. ЕГЭ 2022. Математика. Сборник заданий/В.В. Кочагин, М.Н. Кочагина.– М.:Эксмо, 2022.

Скачано с www.znanio.ru