Конспект урока по теме: Аксиома параллельных прямых

Тема: Аксиома параллельных прямых

 Цели: Дать представление об аксиомах геометрии; ввести аксиому параллельных прямых и следствия из нее.

Тип урока: Комбинированный.

Задачи урока:

Образовательная: Начать формирование у обучающихся представления об аксиоме параллельных прямых и следствий из нее.

Воспитательная: Воспитать у обучающихся интерес к предмету через исторические справки.

Развивающая: Развитие у обучающихся умения сравнивать через проведение изучение новой темы.

Средства урока: мел, доска, готовые чертежи, проектор и диск к учебнику.

План урока

Ход урока

1. Проверка домашнего задания.

Пройти посмотреть выполнение работы.

2. Актуализация опорных знаний.

- Что мы изучали на прошлом уроке?

- Какие прямые называются параллельными?

- Какие признаки параллельных прямых вы знаете? Сформулируйте их.

 3. Изучение нового материала.

Изучение материала из  пункта 27 учебника и из Приложения 1 на с. 344-348 учебника, Приложение 2 на с. 349-351.

Записать в тетрадях: Аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных положений, на основе которых доказываются далее теоремы и строится вся геометрия.

Предложить учащимся задачу, решение которой дано в начале п. 28: через точку А, не лежащую на прямой а, провести прямую, параллельную прямой а. Решение этой задачи доказывает существование прямой, проходящей через данную точку и параллельной данной прямой.

Построение.

1. Провести через точку А прямую b так, что а┴ b.

2. Провести через точку А прямую с так, что b┴с.

Доказательство: <1=  <2=90⁰, т.е. накрест лежащие углы равны при прямых а и с секущей b, следовательно а‖с.

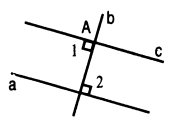
Смотрим построение.

- Всегда ли можно провести такую прямую?

- Сколько таких прямых можно провести?

Рассказать учащимся о том, что в геометрии Евклида, изложенной им в книге «Начала» ответ на данный вопрос следует из знаменитого пятого постулата. Пятый постулат знаменит тем, что долгие годы его пытались доказать на основе остальных аксиом Евклида. И лишь в прошлом веке, было доказано, что пятый постулат не может быть выведен из остальных аксиом. Поэтому утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, принимается в качестве аксиомы.

- Является ли утверждение: «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной» аксиомой? Почему? (нет, оно доказывается)

- Чем отличается вышеуказанное утверждение от аксиомы параллельных прямых? ( в аксиоме говорится о единственности такой прямой)

4.Закрепление изученного материала.

Устно решить задачу №197.

Полезно на рисунке показать учащимся два возможных случая расположения прямых:

1) все четыре прямые пересекают прямую р;

2) одна из четырех прямых параллельна прямой р, а три другие прямые пересекают ее.

Эти два случая иллюстрируют ответ на вопрос задачи: по крайней мере, три прямые пересекают прямую р.

Разъяснение смысла понятия «следствия».

Записать в тетрадях: следствиями называются утверждения, которые выводятся непосредственно из аксиом или теорем.

Рассмотреть следствия 1° и 2° из аксиомы параллельных прямых.

 № 199

Решение.

Прямые ВС и АС имеют общие точки с прямой АВ, т.е. ВС и АС пересекают АВ, значит они пересекают и прямую р, т.к. по условию задачи АВ ׀׀р и из следствия из аксиомы параллельных прямых «если прямая пересекает одну из параллельных прямых, то она пересекает и другую».

 №200.

Решение.

Прямая АD пересекает прямые АВ, АЕ и АС в точке А и прямые ВС и РQ.

АD ׀׀р, значит р пересекает прямые АВ, АЕ, АС, ВС и РQ по следствию: если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

5. Формирование умений и навыков.

Решение задачи № 218:

Отметим произвольную точку, не лежащую на прямой b, и проведем через нее прямую с, параллельную прямой b. Так как прямая а пересекает прямую b, то она пересекает и прямую с. Таким образом, прямая с пересекает прямую а и параллельна прямой b.

Решение задачи № 219*.

Предположим противное, что прямые а и b не параллельны, то есть пересекаются. Тогда можно провести прямую с, которая пересекает прямую а и не пересекает прямую b (из решения задачи № 218). Но это противоречит условию задачи. Значит, наше предположение неверно и а || b.

 7. Итоги урока.

- Что нового вы сегодня узнали?

- С какими понятиями познакомились?

- Сформулируйте определение аксиомы, следствия.

- Сколько следствий из аксиомы параллельных прямых вы знаете? Сформулируйте их.

  8. Домашнее задание: п. 27 и 28 с. 59-62; №198, 217