Конспект урока по теме "Повторение. Многогранники и тела вращения"

Тема «Повторение. Многогранники и тела вращения»

Цель: закрепление формул площади поверхности и объема, свойств пространственных фигур.

Задачи:1.совершенствовать навыки решения задач по теме «Повторение. Многогранники и тела вращения»;

2.способствовать развитию грамотной математической речи,  умению выделять главное, точно формулировать мысль ;

3.способствовать воспитанию  взаимопомощи, воли и настойчивости в достижении поставленной цели, интереса к специальности.

Формирование общих компетенций:

ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности.

ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие.

ОК 04. Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами.

ОК 05. Осуществлять устную и письменную коммуникацию на государственном языке с учетом особенностей социального и культурного контекста.

ОК 06. Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей.

ОК 09. Использовать информационные технологии в профессиональной деятельности.

Тип урока: урок обобщения и систематизации знаний.

Вид урока: урок – практикум.

Оборудование и оснащение: дидактические карточки с заданиями.

План урока:

Сценарий урока:

Самостоятельная работа по группам

1 группа

Прямоугольный параллелепипед

1.   Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.

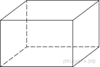
2.  В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ рёбра CD, CB и диагональ CD₁ боковой грани равны соответственно 2, 4 и  Найдите площадь поверхности параллелепипеда ABCDA₁B₁C₁D₁.

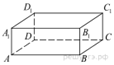
3.  В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ рёбра AB, BC и диагональ боковой грани BC₁ равны соответственно 7, 3 и  Найдите объём параллелепипеда ABCDA₁B₁C₁D₁.

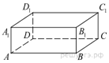
4.  Два ребра прямоугольного параллелепипеда равны 7 и 4, а объём параллелепипеда равен 140. Найдите площадь поверхности этого параллелепипеда.

Куб

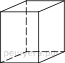
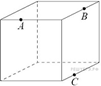
1. Плоскость, проходящая через три точки A, B и C, разбивает куб на два многогранника. Сколько граней у многогранника, у которого больше граней?

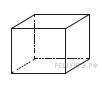
2.  Ящик, имеющий форму куба с ребром 10 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.

3.  Аквариум имеет форму куба со стороной 40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров

2 группа

Призма

1. В сосуд, имеющий форму правильной треугольной призмы, налили 2300  воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в .

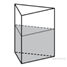
2.  В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.

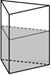
3.  Плоскость, проходящая через три точки A, B и С, разбивает правильную треугольную призму на два многогранника. Сколько рёбер у многогранника, у которого больше вершин?

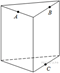
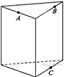
4.  Плоскость, проходящая через три точки   и  разбивает правильную треугольную призму на два многогранника. Сколько вершин у многогранника, у которого меньше граней?

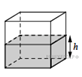
5. Вода в сосуде, имеющем форму правильной четырёхугольной призмы, находится на уровне h = 10 см. На каком уровне окажется вода, если её перелить в другой сосуд, имеющий форму правильной четырёхугольной призмы, у которого сторона основания втрое меньше, чем у данного? Ответ дайте в сантиметрах.

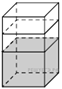
6. В бак, имеющий форму правильной четырёхугольной призмы, налито 8 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

3 группа

Пирамида

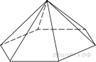
1.  Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

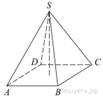
2.  Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

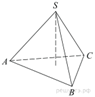
3. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .

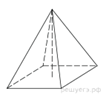
4.  Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно 

5. В основании пирамиды SABC лежит правильный треугольник ABC со стороной 10, а боковое ребро SA перпендикулярно основанию и равно  Найдите объём пирамиды SABC.

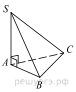
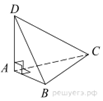
6.  В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB = 6, AC = 18 и AD = 8.

4 группа

Цилиндр

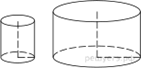
1.  Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 6, а второго — 6 и 7. Во сколько раз объём второго цилиндра больше объёма первого?

2.  Радиус основания цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.

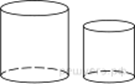
3.  Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 18, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

Конус

1.  Объём конуса равен 50π, а его высота равна 6. Найдите радиус основания конуса

.

2.  Объём конуса равен 32. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.

3. Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?

Индивидуальное задание

Шар

1.  Даны два шара с радиусами 5 и 1. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

2.  Даны два шара с радиусами 4 и 1. Во сколько раз объём большего шара больше объёма другого?

3.  Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?