Конспект урока "Решение задач с помощью системы уравнений"

 

Решение задач с помощью системы уравнений

 

 Класс: 7

 Тип урока: Ознакомление с новым материалом

 Цели урока:

- обучающие:

-  отработка навыков решения систем уравнений,

- отработка навыка решения уравнений по правилу нахождения неизвестных  членов уравнения;

-   познакомить детей с алгоритмом решения задач при помощи системы уравнений.

- развивающие:

- развитие мышления через обучение анализировать, сравнивать, строить аналогии;

- развитие культуры устной и письменной речи;

- развивать способность четко формулировать свои мысли;

- развитие и закрепление навыков устного счета

- воспитательные:

- воспитание уверенности в своих силах;

- прививать любовь к предмету, знакомя детей с высказываниями великих людей

 

  Данный урок предпоследний перед написанием контрольной работы по теме                         « Системы двух уравнений с двумя неизвестными».    

      Урок разработан с использованием  развивающей и проблемной технологий

 

                                  Ход урока

  I  Организационный момент:

 

   Хочу начать этот урок словами Софьи Васильевны Ковалевской: «Многие, которым никогда не представлялось случая более узнать математику, смешивают её с арифметикой и считают наукой сухой. В сущности же эта наука, требующая наиболее фантазии, и нельзя быть математиком не будучи поэтом в душе.»

Да, в математике много интересного, и красоту математики надо уметь увидеть. Одна из красивых тем математики – это решение систем уравнений. А красотой этой части математики является и то, что решить систему можно разными способами. Мы уже познакомились с ними. Что это за способы?

- графический способ;

- способ подстановки;

- способ сложения.

Вспомним их.

 

 

II Повторение пройденного.

Задание: решить систему уравнений:

 

     у – 2х = 0

  у + 3х = 6

 

1. Решим эту систему графически.

Ребенок решает систему у школьной доски

 

Для этого в каждом уравнении выразим у через  х

 

у = 2х  (1)

у = - 3х + 6  (2)

 

Напишем таблички значений х  и  у  для каждого из уравнений

 

х	0	1
у	0	2

 (1)    

 

 

(2)

х	0	1
у	6	3

            

 

 

По данным табличек построим графики функций и найдем координату точки пересечения.

 

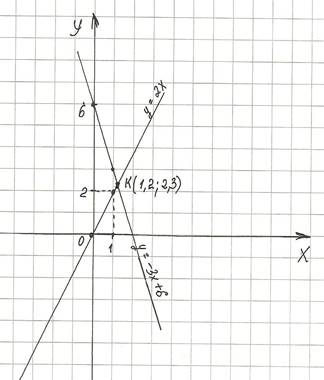
Ответ:  х = 1,2;  у = 2,3

 

 

2. Решим эту систему способом подстановки.

Дети решают в рабочих тетрадях в диалоге с учителем.

 

  у – 2х =0

  у + 3х = 6

 

В первом уравнении выражаем у через х

у = 2х  (1)

 у + 3х = 6  (2)

 

Подставляем  (1)  во второе:

 

 2х + 3х = 6

     5х = 6

      х =

      х = 1,2

Подставляем значение   х  в первое уравнение:

 

  у = 2 ^. 1,2 = 2,4

Ответ: х = 1,2; у = 2,4

 

3. Решим эту систему способом сложения.

 Дети выполняют задание в рабочих тетрадях:

 

у – 2х = 0        __

у + 3х = 6

      5х = 6

       х  = 1,2

у = 2,4

Ответ: х = 1,2; у = 2,4

 

Скажите, пожалуйста, каким способом решать  проще?

Дети отвечают: способом сложения

 

 А когда удобно решать способом подстановки?

Выясняем, что этот способ удобен, когда в одном из уравнений коэффициент при одном из неизвестном равен 1.

 

Что можно сказать про графический способ?

Выясняем, что плюс этого способа в наглядности, но он не точен.

 

Далее учитель говорит, что при помощи систем уравнений можно решать задачи.

Сейчас мы поучимся это делать.

 

 

III  Знакомство с новым материалом

 

 Для решения задач с помощью системы уравнений воспользуемся  АЛГОРИТМОМ:

 

1.      Составить по условию задачи 2 уравнения с 2-мя неизвестными;

2.      Решить систему уравнений;

3.      Записать ответ задачи

 

Предлагаю детям решить задачи: ( тексты  задач распечатаны на карточках)

 

1.    За 4 блокнота и 3 карандаша заплатили 181 руб., а за такие же 2 блокнота и 5 карандашей заплатили 115 р. Сколько стоит 1 блокнот и 1 карандаш?

 

Иногда для решения задачи удобно составить таблицу:

 

	Цена за   1 шт	Цена за   2 шт	Цена за  3 шт	Цена за  4 шт	Цена за  5 шт
Блокнот	х	2х	-----	4х	----
Карандаш	у	-----	3у	-----	5у

 

Зная стоимость 4-х блокнотов и 3-х карандашей, составляем уравнение:

                                   4х + 3у = 181

Зная стоимость  2-х блокнотов и 5-ти карандашей, составляем уравнение:

                                   2х + 5у = 115

Составляем систему уравнений и решаем её способом сложения:

 

            4х + 3у = 181

            2х + 5у = 115       ^. ( -2)

 

 

      4х + 3у = 181       +

    - 4х – 10у = -230      

 

              - 7у = - 49

                  у  = 7

 

Подставляем значение  у  в первое уравнение системы:

 

      4х + 3 ^. 7 = 181

             4х = 160

               х = 40

 

 

Ответ:  1 блокнот стоит 40 рублей; 1 карандаш стоит 7 рублей

 

 

 

2.      Боковая сторона равнобедренного треугольника на 4см длиннее основания.

Найти стороны треугольника, если его периметр равен 25см.

 

 

Обозначим боковую сторону за  х, тогда основание – у

 

Зная, что основание длиннее боковой стороны на 4см, составим уравнение:

                  у – х = 4

 

Зная, что периметр треугольника равен 25см, составим уравнение:

                2х + у = 25

 

Составляем систему уравнений:

               у – х = 4

             2х + у = 25   

 

 Предлагаю решить её способом подстановки:

         у = х + 4    (1)

        2х + у = 25  (2)

 

Подставляем  (1)  во (2):

   2х + х + 4 = 25

           3х = 21

             х = 7

 

Подставляем значение  х  в 1-ое уравнение системы и находим  у:

          у = х + 4

          у = 7 + 4

          у = 11

Ответ:  боковая сторона треугольника равна 7см, основание – 11см

 

 

IV  Самостоятельная работа детей

 

  Детям выдаются карточки с текстом задачи:

 

   Разность двух чисел равна 16, а их сумма равна 26.

Найти эти числа.

 

V Постановка домашнего задания