
Предмет: Геометрия
Класс: 9 класс
Ц е л и : создать условия для доказательства теоремы косинусов; способствовать развитию умения
применять теорему косинусов при решении задач.
1.Организационный момент.
2.Актуализация знаний
На прошлых уроках мы познакомились с новыми значениями косинуса, синуса и тангенса, используя единичную полуокружность.
Какую полуокружность называют единичной?
Полуокружность называется единичной, если ее центр находится в начале координат, а радиус равен 1. Чему равен синус и косинус острого угла ? sin = y, cos = x.
В каких пределах находится значение синуса, косинуса? 0 ≤ sin ≤ 1, - 1≤ cos ≤ 1.
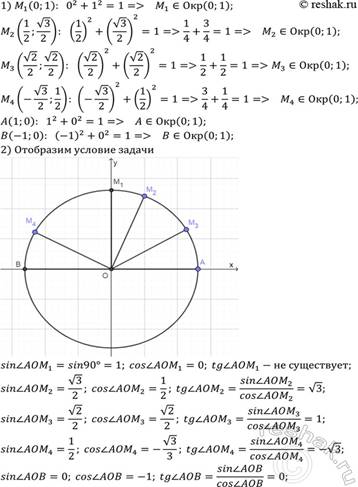
Назовите значения синуса, косинуса и тангенса углов
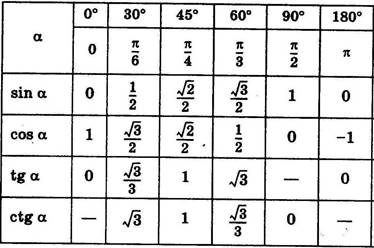
Какое
равенство называется основным тригонометрическим тождеством и
выполняется для любого угла от нуля градусов до ста восьмидесяти градусов. ![]() 1
1
Как называются формулы, которые позволяют упростить вычисления синусов и косинусов углов. Эти формулы называются формулами приведения:
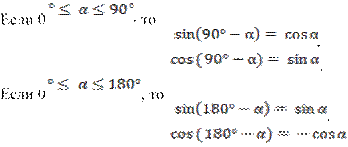
Самостоятельная работа. Формулы привидения.
|
Самостоятельная работа. Формулы привидения. 1 вариант. 1.Запишите формулы привидения для
sin ,
cos ,
если 0 2. Используя формулы привидения вычислите значение тригонометрического числового выражения Sin 1500 cos 1200 Sin 1350 3. Найти косинус острого угла, если его синус равен
4. Вычисляя синус острого угла, ученик получил число 1,5. Верны ли его вычисления?
|
Самостоятельная работа. Формулы привидения. 1 вариант. 1.Запишите формулы привидения для
sin ,
cos ,
если 0 2. Используя формулы привидения вычислите значение тригонометрического числового выражения Sin 1200 cos 1500 cos 1350 3.
Найдите
синус острого угла если его косинус равен 4. Вычисляя косинус острого угла, ученик получил число 0,3. Верны ли его вычисления? 5. Катеты прямоугольного треугольника равны
2√𝟏𝟗 и 18. найдите косинус наименьшего угла этого треугольника.
|
|
ОТВЕТЫ 1.
Если 0
2.
4.НЕТ 5.
Пусть
катеты имеют длины a и b, а гипотенуза — длину
Наименьший угол в треугольнике лежит против наименьшей
стороны,
|
ОТВЕТЫ 1.
Если 0
2.
/2
3. 7/25 4.да 5. Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора: АС^2 + ВС^2 = АВ^2; 18^2 + (2√19)^2 = АВ^2; 324 + 4 * 19 = АВ^2; 324 + 76 = АВ^2; 400 = АВ^2; АВ = 20; 2) Косинус угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Следовательно: cos А = АС/АВ; cos А = 18/20; cos А = 9/10. Ответ: cos А = 9/10. |
3.Изучение нового материала.
Мы с вами уже изучили несколько теорем, которые мы применяем при решении прямоугольных треугольников. Сегодня мы изучим еще одну важную теорему- Теорему косинусов. Теорему косинусов иногда называют обобщенной теоремой Пифагора.
Прежде чем мы перейдем к теореме изучим формулу расстояния между точками.

Теорема
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Выполним первое задание

4. Закрепление изученного материала (решение задач).
Задачи по готовым чертежам. По группам. При решении задач учащиеся каждый раз проговаривают формулировку теоремы.
Задача 1
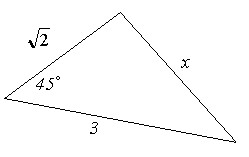
Ответ:
![]() .
.
Задача 2
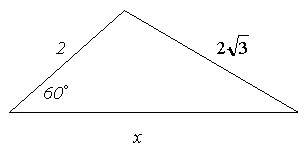 Ответ:
4.
Ответ:
4.
Задача 3
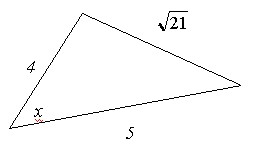 Ответ:
60
Ответ:
60

№1012
№1013

№1015
5. Итог урока.Рефлексия.
Домашняя работа. П.102

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.