Поделиться
Контрольная работа №3.docx
Контрольная работа №3
по теме «Неравенства»
Демоверсия
1. Докажите неравенство: а)(x+1)²>x(x+2) б) a²+1≥2(3a-4)
2. Известно, что а < b. Сравните: а) 19 а и 19 b; б) –5,2а и –5,2b; в) 2,7 b и 2,7а. Результат сравнения запишите в виде неравенства.
3. Решите неравенство: a) 2x2+5x-7<0 б)5x2-4x+21>0
4. Решите неравенство методом интервалов:
а) (х + 4)(х - 6)>0; б)
5. Решите систему неравенств:
{3x−1>2
{5x−10<5
Вариант 1
1. Докажите неравенство: a) (x–2)2 > x(x–4); б) а2+1 ≥ 2(3а–4).
2. Известно, что а < b. Сравните: а) 21а и 21b; б) –3,2а и –3,2b; в) 1,5b и 1,5а. Результат сравнения запишите в виде неравенства.
3. Решите неравенства:
а) х2 - 2х – 8 < 0; б) 2х2
- 5х +3
.
4. Решите неравенство методом интервалов:
а) (х + 9)(х - 5)
;
б) 
5. Решите систему неравенств:
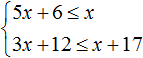
Вариант 2
1. Докажите неравенство: a) (x + 7)2 > x(x + 14); б) b2 + 5 ≥ 10(b – 2).
2. Известно, что а > b. Сравните: а) 18а и 18b; б) –6,7а и –6,7b; в) –3,7b и –3,7а. Результат сравнения запишите в виде неравенства.
3. Решите неравенства:
а) х2 + 4х – 12 < 0; б) 3х2
- 4х +1
.
4. Решите неравенство методом интервалов:
а) (х + 12)(х - 7)
;
б) 
5. Решите систему неравенств:
Ответы:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
|
1 вариант |
а)4 > 0 б) (a – 3)2 ≥ 0 |
а)< б)> в)> |
а) (-2; 4) б)(-∞;1]U [1,5;+ ∞)
|
а) (-∞;-9) U (5;+ ∞) б) (-6;3] |
а) х < 1,5
|
|
2 вариант |
а) 49 > 0 б) (b – 5)2 ≥ 0 |
а)> б)< в)> |
а) (-6; 2) б) (-∞;1/3)U (1;+ ∞) |
а) (-12; 7) б) (-∞;-5] U [(10;+ ∞) |
а) х > 0,25
|
Критерии оценивания
|
Отметка |
«2» |
«3» |
«4» |
«5» |
|
Кол-во баллов |
0-1 |
2 |
3-4 |
5 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
