Контрольная работа по теме: "Многогранники"

Контрольная работа по теме: «Многогранники»

Решение 2 варианта.

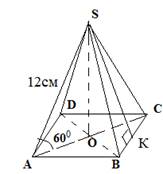
1)     

S_бок = Pl (теорема о площади боковой поверхности правильной пирамиды,

с. 64).

Р = 4АВ. Так как пирамида правильная, то АВ = АС = ВС = АD = х.

Основание – квадрат, АО = ОС. Из треугольника АОS: АО = АS · соs60⁰ = 12 ·   = 6 (см) (АО можно найти, используя свойство прямоугольного треугольника с углом 30⁰). АС = 2АО = 12 см. Из треугольника АВС по теореме Пифагора: АС² = АВ² + ВС², 12² = х² + х², 2х² = 12,  х = , Р = 4.

В треугольнике ВКS проведём апофему пирамиды КS = l = ,

 ВS = 12 см, ВК = ВС =  см, так как треугольник ВКS равнобедренный (боковые грани у правильной пирамиды – равнобедренные треугольники).

КS = l =  =  (см)

S_бок = 4 = 6 (см²)

Ответ: 6 см²

2)     

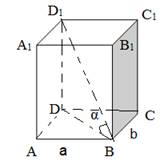
S = 2S_осн + S_бок, S_осн = аb, S_бок = 2(S_АВВ1А1 + S_ВСС1В1).

Из треугольника ВDD₁ найдём DD₁ = ВDtgα.

Из треугольника АВD по теореме Пифагора ВD =  = , то

DD₁ =  tgα., S_АВВ1А1 = а tgα,  S_ВСС1В1 = b  tgα,

S_бок = 2 tgα, S = 2аb + 2 tgα

Ответ: 2аb + 2 tgα

3)     

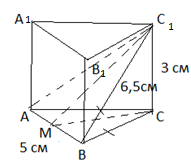
S_АВС – искомое сечение, равнобедренный треугольник (АС = ВС – диагонали равных  боковых граней). Проведём высоту МС (С – середина АВ).

S_АВС = АВ · МС₁. Из треугольника МВС₁ найдём МС₁ =  =  =  = 6, S_АВС =  · 5· 6 = 15 (см²).

Ответ: 15 см²