
МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
Государственное автономное профессиональное образовательное учреждение Московской области
«Егорьевский техникум»
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
ПО МАТЕМАТИКЕ
к программе подготовки специалистов среднего звена
по специальности
15.02.12 «Монтаж, техническая эксплуатация и ремонт
промышленного оборудования (по отраслям)»
2022 г.
ОДОБРЕНО цикловой методической комиссией преподавателей дисциплин общеобразовательного цикла (математики, физики, астрономии, химии, биологии, естествознания, экологии, географии, информатики, основ проектной деятельности) в группах СПО ППССЗ и в группах СПО ППКРС. Председатель ЦМК _________________Н.М.Питахина Протокол № ____ от «____» _____________20___г.
|
РАЗРАБОТАНО на основе - Федерального государственного образовательного стандарта (ФГОС) среднего общего образования (приказ Минобрнауки России от 17.05.2012 № 413 (ред. от 29.06.2017) - Федерального государственного образовательного стандарта (ФГОС) по специальности 15.02.12 «Монтаж, техническая эксплуатация и ремонт промышленного оборудования (по отраслям)», утвержденного 09.12.2016 г. приказом Минобрнауки России № 1580
Заместитель директора по учебной работе __________ С.Г. Большова
|
Составитель: Худякова А.Е., преподаватель математики ГАПОУ МО «Егорьевский техникум», высшей квалификационной категории
СОСТАВ КОМПЛЕКТА КИМ
|
1. |
Паспорт комплекта оценочных (контрольно-измерительных) материалов |
4 |
|
1.1 |
Область применения |
4 |
|
1.2 |
Описание процедуры оценки и системы оценивания по программе |
4 |
|
1.2.1 |
Общие положения об организации оценки |
4 |
|
1.2.2 |
Распределение оценивания результатов обучения по видам контроля |
9
|
|
1.2.3 |
Распределение типов контрольных заданий по элементам знаний и умений |
13
|
|
2. |
Текущий контроль по элементам программы |
19 |
|
2.1 |
Подготовка сообщений, рефератов |
19 |
|
2.2 |
Практические работы
|
23 |
|
2.3 |
Самостоятельные работы |
47 |
|
2.4 |
Тестирование |
51 |
|
2.5 |
Устный опрос и устные задания |
61 |
|
2.6 |
Письменный опрос |
65 |
|
2.7 |
Индивидуальное собеседование |
67 |
|
2.8 |
Контрольные работы |
71 |
|
3. 4. |
Промежуточная аттестация Методические указания для обучающихся с ограниченными возможностями здоровья |
77 79 |
|
|
|
|
1. ПАСПОРТ КОМПЛЕКТА ОЦЕНОЧНЫХ
(КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ) МАТЕРИАЛОВ
1.1. Область применения
Комплект оценочных (контрольно-измерительных) материалов (далее КИМ) предназначен для оценки по специальностям 15.02.12 «Монтаж, техническая эксплуатация и ремонт промышленного оборудования (по отраслям)» результатов освоения обучающимися содержания программы общеобразовательной профильной учебной дисциплины ПД.01 Математика
1.2. Описание процедуры оценки и системы оценивания по программе
1.2.1. Общие положения об организации оценки
Уровень освоения содержания программы общеобразовательной профильной учебной дисциплины ПД.01 Математика обучающимися оценивается путем использования различных типов, видов и форм контроля:
Типы: педагогический, взаимоконтроль, самоконтроль.
Виды:
- входной (в начале 1 курса с целью выявления остаточных знаний),
- текущий (на уроках проверки знаний и умений с целью выявления уровня освоения небольших дидактических единиц),
- обобщающий (по итогам изучения тем на уроках-зачетах)
- промежуточная аттестация (итоговый контроль) (по завершению изучения всего курса математики).
Формы: зачеты, самостоятельные работы, практические работы, устный опрос, контрольные работы и т.д.
Инструментарий: тесты, карточки-задания, кроссворды, домашние задания и т.д.
Оценке в ходе освоения учебной дисциплины «Математика» подлежат результаты:
1. личностные:
1.1 ЛР 7 - Осознающий приоритетную ценность личности человека; уважающий собственную и чужую уникальность в различных ситуациях, во всех формах и видах деятельности.
1.2 ЛР 11 - Проявляющий уважение к эстетическим ценностям, обладающий основами эстетической культуры.
1.3 ЛР 22 - Работающий в коллективе и команде, эффективно взаимодействующий с коллегами, руководством, клиентами.
1.4 ЛР 26 - Проявляющий доброжелательность к окружающим, деликатность, чувство такта и готовый оказать услугу каждому кто в ней нуждается.
2. метапредметные:
2.1умение самостоятельно определять цели деятельности и составлять планы
деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные
стратегии в различных ситуациях;
2.2 умение продуктивно общаться и взаимодействовать в процессе совместной
деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
2.3 владение навыками познавательной, учебно-исследовательской и проектной
деятельности, навыками разрешения проблем; способность и готовность к
самостоятельному поиску методов решения практических задач, применению
различных методов познания;
2.4 готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;
2.5владение языковыми средствами: умение ясно, логично и точно излагать
свою точку зрения, использовать адекватные языковые средства;
2.6 владение навыками познавательной рефлексии как осознания совершаемых
действий и мыслительных процессов, их результатов и оснований, границ
своего знания и незнания, новых познавательных задач и средств для их
достижения;
2.7 целеустремленность в поисках и принятии решений, сообразительность и
интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;
- для глухих, слабослышащих, позднооглохших обучающихся:
2.8владение навыками определения и исправления специфических ошибок (аграмматизмов) в письменной и устной речи.
- для обучающихся с расстройствами аутистического спектра:
2.9 способность планировать, контролировать и оценивать собственные учебные действия в соответствии с поставленной задачей и условиями ее реализации при сопровождающей помощи педагогического работника и организующей помощи тьютора;
2.10 овладение умением определять наиболее эффективные способы достижения результата при сопровождающей помощи педагогического работника и организующей помощи тьютора;
2.11 овладение умением выполнять действия по заданному алгоритму или образцу при сопровождающей помощи педагогического работника и организующей помощи тьютора;
2.12 овладение умением оценивать результат своей деятельности в соответствии с заданными эталонами при организующей помощи тьютора;
2.13 овладение умением адекватно реагировать в стандартной ситуации на успех и неудачу, конструктивно действовать даже в ситуациях неуспеха при организующей помощи тьютора;
2.14 овладение умением активного использования знаково-символических средств для представления информации об изучаемых объектах и процессах, различных схем решения учебных и практических задач при организующей помощи педагога-психолога и тьютора;
2.15 способность самостоятельно обратиться к педагогическому работнику (педагогу-психологу, социальному педагогу) в случае личных затруднений в решении какого-либо вопроса;
2.16 способность самостоятельно действовать в соответствии с заданными эталонами при поиске информации в различных источниках, критически оценивать и интерпретировать полученную информацию из различных источников.
3. предметные:
3.1 сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;
3.2 сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
3.3владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач;
3.4 владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
3.5 сформированность представлений об основных понятиях математического
анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
3.6 владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
3.7 сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире,
основных понятиях элементарной теории вероятностей; умений находить и
оценивать вероятности наступления событий в простейших практических
ситуациях и основные характеристики случайных величин;
3.8 владение навыками использования готовых компьютерных программ при
решении задач.
4. Общие компетенции:
ОК. 01 Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам.
ОК.02 Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельностью
ОК.04 Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами.
ОК.09 Использовать информационные технологии в профессиональной деятельности.
Комплект КИМ для проведения текущего контроля и промежуточной аттестации по учебной дисциплине ПД.01 Математика разработан в соответствии с требованиями:
- ФГОС среднего общего образования (приказ Минобрнауки России от 17.05.2012 № 413 (ред. от 29.06.2017)
- Федерального государственного образовательного стандарта (ФГОС) по специальности 15.02.12 «Монтаж, техническая эксплуатация и ремонт промышленного оборудования (по отраслям)», утвержденного 09.12.2016 г. приказом Минобрнауки России № 1580
- рабочей программы учебной дисциплины ПД.01 Математика, утвержденной Директором ГАПОУ МО «Егорьевский техникум» 27.08.2021 года.
КИМ включают контрольные материалы для проведения текущего контроля и промежуточной аттестации в форме письменного экзамена.
1.2.2 Распределение оценивания результатов обучения по видам контроля
|
Наименование элемента умений или знаний |
Виды аттестации |
|
|
Текущий контроль |
Промежуточная аттестация |
|
|
личностные: |
Экзамен в письменной форме |
|
|
1.1 ЛР 7 - Осознающий приоритетную ценность личности человека; уважающий собственную и чужую уникальность в различных ситуациях, во всех формах и видах деятельности. |
Участие в олимпиадах и конкурсах Подготовка сообщений и рефератов Индивидуальные собеседования |
|
|
1.2 ЛР 11 - Проявляющий уважение к эстетическим ценностям, обладающий основами эстетической культуры. |
Подготовка сообщений и рефератов Индивидуальные собеседования Устный опрос |
|
|
1.3 ЛР 22 - Работающий в коллективе и команде, эффективно взаимодействующий с коллегами, руководством, клиентами. |
Подготовка сообщений и рефератов Практические работы |
|
|
1.4 ЛР 26 - Проявляющий доброжелательность к окружающим, деликатность, чувство такта и готовый оказать услугу каждому кто в ней нуждается.
|
Подготовка сообщений и рефератов Индивидуальные собеседования Устный опрос |
|
|
2. метапредметные: |
||
|
2.1умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях; |
Подготовка сообщений и рефератов Практические работы Тестирование
|
Экзамен в письменной форме. |
|
2.2 умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты; |
Подготовка сообщений и рефератов Участие в олимпиадах и конкурсах
|
|
|
2.3 владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания; |
Подготовка сообщений и рефератов Устные задания Участие в олимпиадах и конкурсах
|
|
|
2.4 готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников; |
Подготовка сообщений и рефератов Устный опрос |
|
|
2.5 владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства; |
Подготовка сообщений и рефератов Устный опрос |
|
|
2.6 владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения; |
Подготовка сообщений и рефератов
|
|
|
2.7 целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира; |
Подготовка сообщений и рефератов Практические работы
|
|
|
2.8владение навыками определения и исправления специфических ошибок (аграмматизмов) в письменной и устной речи. |
Устный и письменный опрос |
|
|
2.9 способность планировать, контролировать и оценивать собственные учебные действия в соответствии с поставленной задачей и условиями ее реализации при сопровождающей помощи педагогического работника и организующей помощи тьютора; |
Индивидуальное собеседование Практические работы
|
|
|
2.10 овладение умением определять наиболее эффективные способы достижения результата при сопровождающей помощи педагогического работника и организующей помощи тьютора; |
Индивидуальное собеседование |
|
|
2.11 овладение умением выполнять действия по заданному алгоритму или образцу при сопровождающей помощи педагогического работника и организующей помощи тьютора; |
Индивидуальное собеседование |
|
|
2.12 овладение умением оценивать результат своей деятельности в соответствии с заданными эталонами при организующей помощи тьютора; |
Индивидуальное собеседование |
|
|
2.13 овладение умением адекватно реагировать в стандартной ситуации на успех и неудачу, конструктивно действовать даже в ситуациях неуспеха при организующей помощи тьютора; |
Индивидуальное собеседование |
|
|
2.14 овладение умением активного использования знаково-символических средств для представления информации об изучаемых объектах и процессах, различных схем решения учебных и практических задач при организующей помощи педагога-психолога и тьютора; |
Индивидуальное собеседование |
|
|
2.15 способность самостоятельно обратиться к педагогическому работнику (педагогу-психологу, социальному педагогу) в случае личных затруднений в решении какого-либо вопроса; |
Индивидуальное собеседование |
|
|
2.16 способность самостоятельно действовать в соответствии с заданными эталонами при поиске информации в различных источниках, критически оценивать и интерпретировать полученную информацию из различных источников. |
Индивидуальное собеседование |
|
|
3. предметные: |
||
|
3.1 сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке; |
Подготовка сообщений и рефератов Контрольные работы |
Экзамен в письменной форме. |
|
3.2 сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий; |
Тестирование Контрольные работы |
|
|
3.3владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач; |
Практические работы Тестирование Контрольные работы |
|
|
3.4 владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств; |
Практические работы Тестирование Контрольные работы |
|
|
3.5 сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей; |
Практические работы Тестирование Контрольные работы |
|
|
3.6 владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием; |
Практические работы Контрольные работы Тестирование
|
|
|
3.7 сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин; |
Практические работы Контрольные работы Тестирование
|
|
|
3.8 владение навыками использования готовых компьютерных программ при решении задач. |
Индивидуальное собеседование |
|
|
4. Общие компетенции: |
Экзамен в письменной форме. |
|
|
ОК. 01. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам.
|
Контрольные работы |
|
|
ОК.02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности |
Подготовка сообщений и рефератов Тестирование |
|
|
ОК.04. Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами. |
Практические работы |
|
|
ОК.09. Использовать информационные технологии в профессиональной деятельности. |
Подготовка сообщений и рефератов Тестирование |
|
1.2.3 Распределение типов контрольных заданий по элементам знаний и умений
|
Содержание учебного материала по программе УД |
Тип контрольного задания |
|||
|
1.1 ЛР 7 |
1.2 ЛР 11 |
1.3 ЛР 22 |
1.4 ЛР 26 |
|
|
Раздел 1. Развитие понятия о числе. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 2. Корни, степени и логарифмы. |
||||
|
Тема 2.1. Корни, степени |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 2.2. Логарифм. Логарифм числа. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 2.3. Преобразование алгебраических выражений. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 3. Основы тригонометрии. |
||||
|
Тема 3.1. Основные понятия |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 3.2. Основные тригонометрические тождества |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 3.3. Преобразования простейших тригонометрических выражений |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 3.4. Тригонометрические уравнения и неравенства |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ,ПР |
ПСР, ИС, УО |
|
Раздел 4. Функции, их свойства и графики. |
||||
|
Тема 4.1. Функции. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 4.2. Свойства функции. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 5. Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции |
||||
|
Тема 5.1. Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 6. Начала математического анализа |
||||
|
Тема 6.1. Последовательности. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 6.2. Производная. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 6.3. Первообразная и интеграл. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 7. Уравнения и неравенства |
||||
|
Тема 7.1. Уравнения и системы уравнений. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 7.2 Неравенства. |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 8. Комбинаторика, статистика и теория вероятностей |
||||
|
Тема 8.1. Элементы комбинаторики |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 8.2. Элементы теории вероятностей |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Тема 8.3. Элементы математической статистики |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 9. Прямые и плоскости в пространстве |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 10. Многогранники |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 11. Тела и поверхности вращения |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Раздел 12. Измерения в геометрии |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
, |
ПСР, ИС, ОК |
ПСР, ИС, УО |
ПСР, ПР |
ПСР, ИС, УО |
|
Содержание учебного материала по программе УД |
Тип контрольного задания |
||||||||||||||||||||||||
|
2.1 |
2.2 |
2.3 |
2.4 |
2.5 |
2.6 |
2.7 |
2.8 |
2.9 |
2.10 |
2.11 |
2.12 |
2.13 |
2.14 |
2.15 |
2.16 |
||||||||||
|
Раздел 1. Развитие понятия о числе. |
ПСР |
ПСР |
ПСР |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 2. Корни, степени и логарифмы. |
|||||||||||||||||||||||||
|
Тема 2.1. Корни, степени |
ПСР |
ПСР, ОК |
ПСР,ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 2.2. Логарифм. Логарифм числа. |
ПСР |
ПСР, ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 2.3. Преобразование алгебраических выражений. |
|
|
|
|
УО, |
|
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 3. Основы тригонометрии. |
|
||||||||||||||||||||||||
|
Тема 3.1. Основные понятия |
ПСР |
ПСР |
ПСР |
ПСР |
УО,ПСР |
ПСР |
ИС,УО |
УО |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 3.2. Основные тригонометрические тождества |
|
ОК |
ОК |
|
УО |
|
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 3.3. Преобразования простейших тригонометрических выражений |
|
|
|
|
УО |
|
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 3.4. Тригонометрические уравнения и неравенства |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 4. Функции, их свойства и графики. |
|
||||||||||||||||||||||||
|
Тема 4.1. Функции. |
ПСР |
ПСР |
ПСР |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 4.2. Свойства функции. |
ПСР |
ПСР |
ПСР |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 5. Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции |
|||||||||||||||||||||||||
|
Тема 5.1. Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 6. Начала математического анализа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Тема 6.1. Последовательности. |
ПСР |
ПСР |
ПСР |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 6.2. Производная. |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 6.3. Первообразная и интеграл. |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 7. Уравнения и неравенства |
|||||||||||||||||||||||||
|
Тема 7.1. Уравнения и системы уравнений. |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 7.2 Неравенства. |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 8. Комбинаторика, статистика и теория вероятностей |
|||||||||||||||||||||||||
|
Тема 8.1. Элементы комбинаторики |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 8.2. Элементы теории вероятностей |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Тема 8.3. Элементы математической статистики |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 9. Прямые и плоскости в пространстве |
ПСР |
ПСР |
ПСР |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 10. Многогранники |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 11. Тела и поверхности вращения |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 12. Измерения в геометрии |
ПСР |
ПСР ОК |
ПСР ОК |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Раздел 13. Координаты и векторы |
ПСР |
ПСР |
ПСР |
ПСР |
УО,ПСР |
ПСР |
ПР,ИС,УО |
УО |
ИС,ПР |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
ИС |
|||||||||
|
Содержание учебного материала по программе УД |
Тип контрольного задания |
|||||||||||
|
3.1 |
3.2 |
3.3 |
3.4 |
3.5 |
3.6 |
3.7 |
3.8 |
ОК.1 |
ОК.2 |
ОК.4 |
ОК.9 |
|
|
Раздел 1. Развитие понятия о числе. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 2. Корни, степени и логарифмы. |
|
|
|
|||||||||
|
Тема 2.1. Корни, степени |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 2.2. Логарифм. Логарифм числа. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т,КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 2.3. Преобразование алгебраических выражений. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 3. Основы тригонометрии. |
||||||||||||
|
Тема 3.1. Основные понятия |
ПСР |
|
,УЗ |
Т,УЗ |
Т, УЗ |
Т |
Т,УЗ |
УЗ |
Т,УЗ |
ПСР,Т,УЗ |
|
ПСР,Т |
|
Тема 3.2. Основные тригонометрические тождества |
КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 3.3. Преобразования простейших тригонометрических выражений |
КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 3.4. Тригонометрические уравнения и неравенства |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 4. Функции, их свойства и графики. |
||||||||||||
|
Тема 4.1. Функции. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 4.2. Свойства функции. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 5. Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции |
||||||||||||
|
Тема 5.1. Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 6. Начала математического анализа |
||||||||||||
|
Тема 6.1. Последовательности. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 6.2. Производная. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 6.3. Первообразная и интеграл. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 7. Уравнения и неравенства |
||||||||||||
|
Тема 7.1. Уравнения и системы уравнений. |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 7.2 Неравенства. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Раздел 8. Комбинаторика, статистика и теория вероятностей |
||||||||||||
|
Тема 8.1. Элементы комбинаторики |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 8.2. Элементы теории вероятностей |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Тема 8.3. Элементы математической статистики |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 9. Прямые и плоскости в пространстве |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 10. Многогранники |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 11. Тела и поверхности вращения |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 12. Измерения в геометрии |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
|
Раздел 13. Координаты и векторы |
ПСР,КР |
Т,КР |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР,УЗ |
ПР,Т,КР |
ПР,Т, КР,УЗ |
УЗ |
Т,КР,УЗ |
ПСР,Т,УЗ |
ПР |
ПСР,Т |
Использованные сокращения по типам контроля:
ПСР – подготовка сообщений, рефератов
ОК – олимпиады, конкурсы
ИС – индивидуальное собеседование
УО – устный опрос
УЗ – устные задания
Т - тестирование
ПР – практическая работа
КР - контрольная работа
2. Текущий контроль по элементам программы
2.1 Подготовка сообщений, рефератов
Виды рефератов
|
По полноте изложения |
Информативные (рефераты-конспекты). |
|
Индикативные (рефераты-резюме). |
|
|
По количеству реферируемых источников |
Монографические. |
|
Обзорные. |
Структура реферата:
1) титульный лист;
2) содержание работы с указанием страниц каждого пункта
3) введение;
4) текстовое изложение материала, разбитое на пункты с необходимыми ссылками на источники;
5) заключение;
6) список использованных источников информации;
7) приложения, которые состоят из таблиц, диаграмм, графиков, рисунков, схем (необязательная часть реферата).
Приложения располагаются последовательно, согласно заголовкам, отражающим их содержание.
Реферат оценивается преподавателем исходя из установленных показателей и критериев оценки реферата.
Критерии и показатели, используемые при оценивании учебного реферата
|
Критерии |
Показатели |
|
1.Новизна текста Макс. - 10 баллов |
- актуальность проблемы
и темы; |
|
2. Степень раскрытия
сущности проблемы |
- соответствие
содержания теме реферата; - умение аргументировать основные положения и выводы. |
|
3.
Обоснованность выбора источников |
- круг, полнота
использования источников по проблеме; |
|
4. Соблюдение требований к оформлению Макс. - 20 баллов |
- правильное
оформление ссылок на используемые источники; |
|
5. Грамотность Макс. - 15 баллов |
- отсутствие
орфографических и синтаксических ошибок, стилистических погрешностей; |
Оценивание реферата:
Реферат оценивается по 100 балльной шкале, балы переводятся в оценки успеваемости следующим образом:
• 86 – 100 баллов – «отлично»;
• 71 – 85 баллов – «хорошо»;
• 56 – 70баллов – «удовлетворительно»;
• менее 55 баллов– «неудовлетворительно».
Баллы учитываются в процессе текущей оценки знаний программного материала.
Критерии оценивания реферата:
1. Соответствие содержания реферата теме.
2. Самостоятельность выполнения работы, глубина проработки материала, использование рекомендованной и справочной литературы
3. Исследовательский характер.
4. Логичность и последовательность изложения.
5. Обоснованность и доказательность выводов.
6. Грамотность изложения и качество оформления работы.
7. Использование наглядного материала.
Оценка «отлично»- учебный материал освоен студентом в полном объеме, легко ориентируется в материале, полно и аргументировано отвечает на дополнительные вопросы, излагает материал логически последовательно, делает самостоятельные выводы, умозаключения, демонстрирует кругозор, использует материал из дополнительных источников, интернет ресурсы. Сообщение носит исследовательский характер. Речь характеризуется эмоциональной выразительностью, четкой дикцией, стилистической и орфоэпической грамотностью. Использует наглядный материал (презентация).
Оценка «хорошо»- по своим характеристикам сообщение студента соответствует характеристикам отличного ответа, но студент может испытывать некоторые затруднения в ответах на дополнительные вопросы, допускать некоторые погрешности в речи. Отсутствует исследовательский компонент в реферате.
Оценка «удовлетворительно»- студент испытывал трудности в подборе материала, его структурировании. Пользовался, в основном, учебной литературой, не использовал дополнительные источники информации. Не может ответить на дополнительные вопросы по теме реферата. Материал излагает не последовательно, не устанавливает логические связи, затрудняется в формулировке выводов. Допускает стилистические и орфоэпические ошибки.
Оценка «неудовлетворительно»- сообщение студентом не подготовлено либо подготовлено по одному источнику информации либо не соответствует теме.
Примерные темы рефератов (сообщений):
1. Волшебный мир многогранников.
2. Гармония в архитектуре – нелинейная перспектива.
3. Геометрические особенности и математические расчеты в творчестве Сальвадора Дали
4. Графическая интерпретация систем уравнений.
5. Египетские пирамиды.
6. Задача Александра Герона “О зеркалах”.
7. Задача Ферма-Торричелли-Штейнера.
8. Зачем решать треугольники, разве мало уравнений?
9. Золотое сечение – гармоническая пропорция.
10. Золотое сечение в искусстве составления букетов.
11. Золотое сечение и многогранники.
12. Золотое сечение и пирамида. Золотое сечение в живописи.
13. Золотое сечение и числа Фибоначчи.
14. Золотые спирали и “пентагональная” симметрия в живой природе.
15. Золотое сечение и симметрия минералов в геологии.
16. Функции в физике и технике.
17. Функция вокруг нас.
18. Логарифмические (золотые) спирали в природе.
19. Математика в искусстве.
20. Математика и архитектура.
21. Математика и гармония в музыке.
22. Метод Гаусса – один из способов решения систем линейных уравнений.
23. Метод координат в геометрии.
24. Модуль в определении предела.
25. Молекулярные тайны жизни и золотое сечение.
26. Неевклидовы геометрии.
27. Неравенство Коши.
28. Неравенство Птолемея и следствия из него.
29. Нетрадиционные способы решения уравнений различных видов.
30. Пирамиды в пропорциях золотого сечения – генератор жизни.
31. Построение графиков функций, содержащих знак абсолютной величины.
32. Преобразование графиков функций.
33. Применение модуля в физике и векторной алгебре.
34. Применение производной в физике и технике.
35. Применение правильных многогранников.
36. Простейшие функции, заданные явно и неявно, аналитическое выражение которых содержит знак модуля.
37. Решение неравенств, содержащих знак абсолютной величины.
38. Решение уравнений, содержащих знак абсолютной величины.
39. Решение систем линейных уравнений с помощью определителей.
40. Ритмы стихосложения и золотое сечение.
41. Ряды. Прогрессии.
42. Создание узоров и орнаментов при помощи построения правильных многоугольников.
43. Способы решения систем уравнений.
44. Способы решения уравнений высоких степеней.
45. Схема Горнера при решении уравнений высоких степеней.
46. Теорема Безу при решении уравнений высоких степеней.
47. Теорема Стюарта и ее применение.
48. Удивительный тетраэдр.
49. Уравнения вокруг нас.
50. Уравнения с параметрами.
51. Применение интегралов в физике и геометрии.
52. Эпоха Ренессанса – эпоха гармонии
2.2 Практические работы
Цель проведения тестовых практических работ:
1. Повторить знания студентов в теме.
2. Организовать деятельность студентов по переводу своих знаний от усвоения отдельных фактов и понятий к их обобщению в целостную систему знаний.
3. Определить уровень усвоения знаний, оценить результат деятельности студентов.
Цель проведения практических работ:
1.Корректировать знания, умения в теме.
2.Закрепить и систематизировать знания по теме.
3.Определить уровень усвоения знаний, оценить результат деятельности студентов.
Тестовая проверка знаний обучающихся предусматривает решение простейших задач, ответы на вопросы. Тесты «закрытого типа» имеют один правильный вариант ответа. Вариантов ответов 4. Время выполнения от 10 до 25 минут (1 вопрос – 1-2минуты). Задания выполняются после прохождения и закрепления материала. Задания обучающиеся выполняют на отдельных листах. Предусматривается 4 варианта заданий в каждой практической работе. Виды проверки: самопроверка, взаимопроверка.
Критерии оценки практической работы.
Оценка за тестовую практическую работу выставляется по следующему алгоритму:
1. Определяется общее количество баллов за работу в целом.
2.Определяется коэффициент усвоения по формуле:
КУ=![]()
![]()
если КУ> 0,9 — 1 - выставляется оценка «отлично»;
если КУ от 0,8 до 0,9 - выставляется оценка «хорошо»;
при КУ от 0,6 до 0,8 - выставляется оценка «удовлетворительно»;
при КУ <0,6 - выставляется оценка «неудовлетворительно».
Составлен сборник практических работ по темам: «Производная», «Преобразование выражений», «Вычисление производной с помощью определения», «Вычисление производных алгебраических функций», «Вычисление производных сложных функций», «Нахождение наибольшего и наименьшего значений функции», «Свойства функций», «Исследование функции и построение ее графика», «Вычисление первообразных функций», «Вычисление определенного интеграла», «Применение интеграла для вычисления площадей и объемов», «Тригонометрические функции углов поворота», «Преобразование тригонометрических выражений», «Решение тригонометрических уравнений», «Преобразование выражений», «Преобразование выражений, содержащих радикалы», «Решение иррациональных уравнений», «Преобразование выражений, содержащих степени с дробными показателями», «Преобразование выражений, содержащих степени и логарифмы», «Решение рациональных уравнений и неравенств», «Решение рациональных уравнений и неравенств», «Решение показательных уравнений и неравенств», «Решение логарифмических уравнений и неравенств», «Углы и расстояния в пространстве», «Двугранный угол», «Перпендикулярность прямой и плоскости», «Параллелепипед», «Призма», «Пирамида», «Цилиндр», «Конус», «Шар. Сфера», «Многогранники и тела вращения», «Элементы комбинаторики и теории вероятностей».
ЦЕЛЬ РАБОТЫ:
1.Повторить знания студентов в теме: «Производная».
2.Организовать деятельность студентов по переводу своих знаний от усвоения отдельных фактов и понятий к их обобщению в целостную систему знаний.
3.Определить уровень усвоения знаний, оценить результат деятельности студентов.
ОБОРУДОВАНИЕ: инструкционно-технологические карты, справочные пособия по математическому анализу, таблицы производных элементарных функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Изучить условие заданий для практической работы (тест).
2. Оформить отчет о работе (форму отчета выбирает преподаватель).
Тест 1. Определение производной.
1 вариант.
1.
Приращение
функции ![]() в точке
в точке ![]() при
при ![]() равно:
равно:
а) –0,19; б) 0,21; в) 0,20; г) –0,09.
2.
Производная
функции ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Производная
функции ![]() в точке
в точке ![]() равна:
равна:
а) 5; б) 4,5; в) 6; г) 3,5.
4.
Какая
из приведенных функций является производной функции ![]() ?
?
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2 вариант.
1.
Приращение функции ![]() в
точке
в
точке ![]() при
при ![]() равно:
равно:
а) 0,42; б) –0,38; в) 0,40; г) –0,39.
2.
Производная функции ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Какая из приведенных функций является производной функции ![]() ?
?
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3 вариант.
1.
Приращение
функции ![]() в точке
в точке ![]() при
при ![]() равно:
равно:
а) –0,19; б) 0,21; в) 0,19; г) –0,21.
2.
Производная
функции ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Производная
функции ![]() в точке
в точке ![]() равна:
равна:
а) –1,5; б) 1,5; в) –0,75; г) 0,75.
4.
Какая
из приведенных функций является производной функции ![]() ?
?
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4 вариант.
1.
Приращение функции ![]() в
точке
в
точке ![]() при
при ![]() равно:
равно:
а) 0,63; б) 0,60; в) –0,59; г) –0,57.
2.
Производная функции ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 1,2; б) 2; в) –1,2; г) 2,5.
4.
Какая из приведенных функций является производной функции ![]() ?
?
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
Тест 2. Правила нахождения производной.
Степенная и тригонометрические функции.
1 вариант.
1.
Производная функции ![]() равна:
равна:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 0,5; б) 1; в) –0,5; г) –1.
4.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 0,5; б) –0,5; в) 1; г) 0.
2 вариант.
1.
Производная функции ![]() равна:
равна:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 0,5; б) 1; в) –0,5; г) –1.
4.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 0,5; б) –0,5; в) 1; г) 0.
3 вариант.
1.
Производная функции ![]() равна:
равна:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 0,5; б) 1; в) –0,5; г) –1.
4.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 0,5; б) –0,5; в) 1; г) 0.
4 вариант.
1.
Производная функции ![]() равна:
равна:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 0,5; б) 1; в) –0,5; г) –1.
4.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) 0,5; б) –0,5; в) 0; г) 1.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
Тест 3. Правила нахождения производной.
Логарифмическая и показательная функции.
1 вариант.
1.
Производная функции ![]() равна
нулю в точках:
равна
нулю в точках:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
![]() .
.
2.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б) 3,5; в) –1,5; г) 1.
;
б) 3,5; в) –1,5; г) 1.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Производная функции 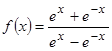 в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2 вариант.
1.
Производная функции ![]() равна
нулю в точках:
равна
нулю в точках:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
![]() .
.
2.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в) 1,5; г)
; в) 1,5; г) ![]() .
.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Производная функции 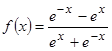 в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3 вариант.
1.
Производная функции ![]() равна
нулю в точках:
равна
нулю в точках:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
![]() .
.
2.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) –1,25; б) ![]() ;
в) –0,75; г) 1,5.
;
в) –0,75; г) 1,5.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Производная функции 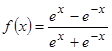 в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4 вариант.
1.
Производная функции ![]() равна
нулю в точках:
равна
нулю в точках:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
![]() .
.
2.
Производная функции ![]() в точке
в точке ![]() равна:
равна:
а) ![]() ;
б) 3; в) 1; г) 1,5.
;
б) 3; в) 1; г) 1,5.
3.
Производная функции ![]() в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Производная функции 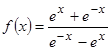 в
точке
в
точке ![]() равна:
равна:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
Тест 4. Геометрический смысл производной.
1 вариант.
1.
Угловой коэффициент секущей к графику функции ![]() ,
проходящей через точки с абсциссами
,
проходящей через точки с абсциссами ![]() равен:
равен:
а) 1,25; б) 0,25; в) 1,5; г) 0,625.
2.
Угловой коэффициент касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() равен:
равен:
а) –1; б) ![]() ;
в) 1; г)
;
в) 1; г) ![]() .
.
3.
Угловой коэффициент касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() равен:
равен:
а) 8; б) 2; в) –2; г) 0.
4.
Уравнением касательной к графику функции ![]() в
точке с абсциссой
в
точке с абсциссой ![]() является:
является:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2 вариант.
1.
Угловой коэффициент секущей к графику функции ![]() ,
проходящей через точки с абсциссами
,
проходящей через точки с абсциссами ![]() равен:
равен:
а) –0,5; б) 0,25; в) –1; г) 0,75.
2.
Угловой коэффициент касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() равен:
равен:
а) 3; б) 4; в) 7; г) ![]() .
.
3.
Угловой коэффициент касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() равен:
равен:
а) ![]() ;
б) 10; в)
;
б) 10; в) ![]() ; г) 6.
; г) 6.
4.
Уравнением касательной к графику функции ![]() в
точке с абсциссой
в
точке с абсциссой ![]() является:
является:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3 вариант.
1.
Угловой коэффициент секущей к графику функции ![]() ,
проходящей через точки с абсциссами
,
проходящей через точки с абсциссами ![]() равен:
равен:
а) 1,25; б) 0,25; в) 1,5; г) –0,75.
2.
Угловой коэффициент касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() равен:
равен:
а) 6; б) 4; в) 8; г) –0,75.
3.
Угловой коэффициент касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() равен:
равен:
а) 0; б) 7; в) –1; г) 1.
4.
Уравнением касательной к графику функции ![]() в
точке с абсциссой
в
точке с абсциссой ![]() является:
является:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4 вариант.
1.
Угловой коэффициент секущей к графику функции ![]() ,
проходящей через точки с абсциссами
,
проходящей через точки с абсциссами ![]() равен:
равен:
а) 3; б) 0,25; в) 1,5; г) –2.
2.
Угловой коэффициент касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() равен:
равен:
а) 4; б) 2,5; в) 1,5; г) 3,5.
3.
Угловой коэффициент касательной к графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]() равен:
равен:
а) 1; б) –1; в) 6; г) 0.
4.
Уравнением касательной к графику функции ![]() в
точке с абсциссой
в
точке с абсциссой ![]() является:
является:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
Тест 5. Физический смысл производной.
1 вариант.
1.
Скорость
точки, движущейся по прямой по закону ![]() ,
равна
,
равна
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Точка
движется по прямой по закону ![]() .
Её мгновенная скорость
.
Её мгновенная скорость ![]() равна:
равна:
а) 8; б) 6; в) 10; г) 9.
3.
Ускорение
точки, движущейся по прямой по закону ![]() равно:
равно:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Тело
массой m движется по закону ![]() . Сила, действующая на
тело в момент времени
. Сила, действующая на
тело в момент времени ![]() ,
равна:
,
равна:
а) 0; б) ![]() ;
в)
;
в) ![]() ; г)
; г) ![]() .
.
2 вариант.
1.
Скорость
точки, движущейся по прямой по закону ![]() ,
равна
,
равна
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Точка
движется по прямой по закону ![]() .
Её мгновенная скорость
.
Её мгновенная скорость ![]() равна:
равна:
а) 11; б) 13; в) 12; г) 10.
3.
Ускорение
точки, движущейся по прямой по закону ![]() равно:
равно:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Тело
массой m движется по закону ![]() . Сила, действующая на
тело в момент времени
. Сила, действующая на
тело в момент времени ![]() ,
равна:
,
равна:
а) 0; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3 вариант.
1.
Скорость
точки, движущейся по прямой по закону ![]() , равна
, равна
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Точка
движется по прямой по закону ![]() .
Её мгновенная скорость
.
Её мгновенная скорость ![]() равна:
равна:
а) 6; б) 8; в) 10; г) 9.
3.
Ускорение
точки, движущейся по прямой по закону ![]() равно:
равно:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Тело
массой m движется по закону ![]() . Сила, действующая на
тело в момент времени
. Сила, действующая на
тело в момент времени ![]() ,
равна:
,
равна:
а) 0; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4 вариант.
1.
Скорость
точки, движущейся по прямой по закону ![]() , равна
, равна
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Точка
движется по прямой по закону ![]() .
Её мгновенная скорость
.
Её мгновенная скорость ![]() равна:
равна:
а) 18; б) 16; в) 20; г) 14.
3.
Ускорение
точки, движущейся по прямой по закону ![]() равно:
равно:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Тело
массой m движется по закону ![]() . Сила, действующая на
тело в момент времени
. Сила, действующая на
тело в момент времени ![]() ,
равна:
,
равна:
а) ![]() ;
б) 0; в)
;
б) 0; в) ![]() ;
г)
;
г) ![]() .
.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
Тест 6. Исследование функций.
1 вариант.
1. Областью
определения функции ![]() является:
является:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2. Область
значений функции ![]() является:
является:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3. Функция
![]() возрастает на промежутке:
возрастает на промежутке:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4. Критическими
(стационарными) точками функции![]() являются:
являются:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ,
,![]() .
.
2 вариант.
1. Областью
определения функции ![]() является:
является:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2. Область
значений функции ![]() является:
является:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3. Функция
![]() убывает на промежутке:
убывает на промежутке:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4. Критическими
(стационарными) точками функции![]() являются:
являются:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ,
,![]() .
.
3 вариант.
1. Областью
определения функции ![]() является:
является:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2. Область
значений функции ![]() является:
является:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3. Функция
![]() убывает на промежутке:
убывает на промежутке:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4. Критическими
(стационарными) точками функции![]() являются:
являются:
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ,
,![]() .
.
4 вариант.
1.
Областью
определения функции ![]() является:
является:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2.
Область
значений функции ![]() является:
является:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3.
Функция
![]() возрастает на
промежутке:
возрастает на
промежутке:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4.
Критическими
(стационарными) точками функции![]() являются:
являются:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ,
,![]() .
.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
Тест 7. Наибольшее и наименьшее значения функции.
1 вариант.
1.
На
отрезке ![]() функция
функция ![]() достигает наибольшего
значения в точке с абсциссой:
достигает наибольшего
значения в точке с абсциссой:
а) –1; б) –2; в) 3; г) 0.
2.
Наименьшее
значение функции ![]() на
интервале
на
интервале ![]() равно:
равно:
а) ![]() ;
б) 2; в)
;
б) 2; в) ![]() ;
г) 2.
;
г) 2.
3. Положительное число, сумма которого со своей обратной величиной имеет наименьшее значение, равно:
а) 1; б) 2; в) ![]() ; г)
; г) ![]() .
.
4. Стороны прямоугольника наибольшей площади при его периметре 12 м равны:
а) 2 и 4 м; б) 3 и 3 м; в) 1 и 5 м; г) 1,5 и 4,5 м.
2 вариант.
1.
На
отрезке ![]() функция
функция ![]() достигает наименьшего
значения в точке с абсциссой:
достигает наименьшего
значения в точке с абсциссой:
а) –1; б) 3; в) 4; г) 0.
2. Наибольшее
значение функции ![]() на
интервале
на
интервале ![]() равно:
равно:
а) ![]() ; б)
; б) ![]() ; в) –2; г)
; в) –2; г) ![]() .
.
3. Число, куб которого превышает утроенный его квадрат на минимальное значение, равно:
а) 1; б) 2; в) ![]() ; г) –1.
; г) –1.
4. Стороны прямоугольника наименьшего периметра при его площади 114 м2 равны:
а) 4 и 36 м; б) 8 и 18 м; в) 12 и 12 м; г) 9 и 16 м.
3 вариант.
1.
На
отрезке ![]() функция
функция ![]() достигает наименьшего
значения в точке с абсциссой:
достигает наименьшего
значения в точке с абсциссой:
а) –1; б) 0; в) 1; г) –2.
2. Наибольшее
значение функции ![]() на
интервале
на
интервале ![]() равно:
равно:
а)
![]() ; б) 0; в)
; б) 0; в) ![]() ; г) 2.
; г) 2.
3. Число, квадрат которого превышает его куб на максимальное значение, равно:
а)
1; б) 2; в) ![]() ;
г) –1.
;
г) –1.
4. Стороны прямоугольника наименьшего периметра при его площади 64 м2 равны:
а) 2 и 32 м; б) 4 и 16 м; в) 6,4 и 10 м; г) 8 и 8 м.
4 вариант.
1. На
отрезке ![]() функция
функция ![]() достигает наибольшего
значения в точке с абсциссой:
достигает наибольшего
значения в точке с абсциссой:
а) –3; б) 2; в) 0; г) –2.
2. Наименьшее
значение функции ![]() на
интервале
на
интервале ![]() равно:
равно:
а)
0; б) ![]() ;
в) 1; г)
;
в) 1; г) ![]() .
.
3. Отрицательное число, сумма которого со своей обратной величиной имеет наибольшее значение, равно:
а)
![]() ; б) –2; в)
; б) –2; в) ![]() ; г) –1.
; г) –1.
4. Стороны прямоугольника наибольшей площади при его периметре 16 м равны:
а) 4 и 4 м; б) 2 и 6 м; в) 3 и 5 м; г) 3,5 и 4,5 м.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
Итого – 28 баллов.
26 – 28 баллов оценка «5»
23 – 25 баллов оценка «4»
20 – 22 баллов оценка «3»
19 и менее оценка «2»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения в теме: «Вычисление производных алгебраических функций».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности студентов.
ОБОРУДОВАНИЕ: инструкционно-технологические карты, таблица производных элементарных функций; микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Сформулируйте определение функции.
б) Сформулируйте правила вычисления производных алгебраических функций.
в) В чем состоит механический смысл производной?
г) Тело движется по прямой согласно закону х(t). Запишите формулы для нахождения скорости и ускорения тела в момент времени t.
2. По образцу выполнить тренировочные задания.
3. Изучить условие заданий для практической работы.
4. Оформить отчет о работе.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ
ПРИМЕР 1. Решите неравенство: ![]() , если
, если ![]() .
.
РЕШЕНИЕ. Пользуясь правилами дифференцирования алгебраических функций и формулами дифференцирования элементарных функций, вычислим производные:
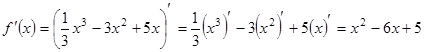 ;
;
![]() .
.
Таким образом, нужно решить неравенство:
![]() .
.
Разложим числитель дроби на множители:
![]() .
.
![]() Неравенство
Неравенство
![]() методом интервалов.
методом интервалов.
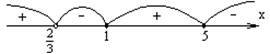
Нули
числителя: х = 1, х = 5. Нуль знаменателя: ![]() .
.
О т в е т: ![]() .
.
ПРИМЕР 2. Тело движется по прямой согласно
закону ![]() . Найдите скорость и
ускорение точки в момент времени
. Найдите скорость и
ускорение точки в момент времени ![]() .
.
РЕШЕНИЕ. Скорость движения – это производная от пути по времени, следовательно,
![]() .
.
Значит, в момент времени ![]() скорость данного
движения такова:
скорость данного
движения такова: ![]() .
.
Так как нам известна скорость движения как функция
времени, мы можем найти ускорение этого
движения: ![]() .
.
Значит, в момент времени ![]() ускорение данного
движения равно:
ускорение данного
движения равно: ![]() .
.
О т в е т: 46; 24.
ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ.
1.
Решите
неравенство ![]() ,
если
,
если ![]() .
.
2.
Тело
движется по прямой согласно закону ![]() . Найдите скорость и
ускорение точки в момент времени
. Найдите скорость и
ускорение точки в момент времени ![]() .
.
Вариант 1.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.
Решите
уравнение ![]() ,
если
,
если ![]() .
.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.
Решите
неравенство ![]() ,
если
,
если ![]() .
.
Вариант 3.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.
Решите
уравнение ![]() ,
если
,
если ![]() .
.
Вариант 4.
1. Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.
Решите
уравнение ![]() ,
если
,
если ![]() .
.
Критерии оценки.
За каждый правильный ответ на контрольные вопросы– начисляется 0,5 балла.
За каждое правильно решенное задание – начисляется 4 балла.
Итого – 10 баллов.
10 баллов оценка «5»
8-9 баллов оценка «4»
6-7 баллов оценка «3»
5 и менее оценка «2»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения в теме: «Применение определенного интеграла для вычисления площадей и объемов».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности студентов.
ОБОРУДОВАНИЕ: инструкционно-технологические карты, таблицы первообразных некоторых функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Какую фигуру называют криволинейной трапецией? Приведите примеры криволинейных трапеций.
б) Запишите формулу для вычисления площади криволинейной трапеции.
в) Покажите на рисунках и запишите интегральные формулы, с помощью которых можно вычислить площади фигур, не являющихся криволинейными трапециями.
г) Запишите и с помощью иллюстрации прокомментируйте интегральную формулу для вычисления объемов тел.
2. С помощью обучающей таблицы повторить план вычисления площади криволинейной трапеции и изучить образцы решенных задач.
3. Выполнить задания для самоконтроля (в таблице).
4. Изучить условие заданий для практической работы.
5. Оформить отчет о работе.
Определение.
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и
не меняющей на отрезке ![]() знака
функции
знака
функции ![]() , прямыми
, прямыми ![]() и отрезком
и отрезком ![]() . Площадь S
криволинейной трапеции находится по формуле
. Площадь S
криволинейной трапеции находится по формуле
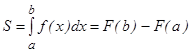 . (*)
. (*)
Задание. Вычислите площадь фигуры, ограниченной линиями:
а) ![]() ; б)
; б) ![]() .
.
|
№ |
План вычисления площади |
Применение |
плана |
|
шага |
криволинейной трапеции |
а) |
б) |
|
|
Строим заданные линии и штриховкой отмечаем фигуру, площадь которой надо найти. Установим, является ли эта фигура криволинейной трапецией |
|
|
|
2 |
Записываем формулу для вычисления площади искомой фигуры |
|
|
|
3 |
Находим пределы интегрирования |
|
|
|
4 |
Вычисляем искомую площадь по формуле (*) |
|
|
Примеры. Вычислите площадь фигуры, ограниченной линиями:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ;
;
5)
![]() ; 6)
; 6) ![]() ;
;
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ.
Вариант 1.
1. Вычислите
площадь фигуры, ограниченной линиями: ![]() .
.
2. ![]() Выберите
правильный вариант ответа.
Выберите
правильный вариант ответа.
Площадь фигуры, изображенной на
рисунке, вычисляется по формуле:
а) 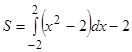 ;
;
б) 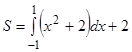 ;
;
в) 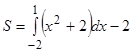 .
.
Вариант 2.
1. Вычислите
площадь фигуры, ограниченной линиями: ![]() .
.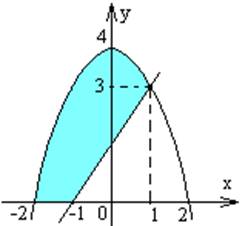
2. ![]() Выберите
правильный вариант ответа.
Выберите
правильный вариант ответа.
Площадь фигуры, изображенной на
рисунке, вычисляется по формуле:
а) 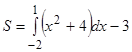 ;
;
б) 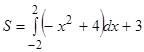 ;
;
в) 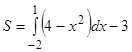 .
.
Вариант 3.
1.
Вычислите
площадь фигуры, ограниченной линиями: ![]() .
.
2. Выберите
правильный вариант ответа. Площадь фигуры, ограниченной
линиями ![]() , равна:
, равна:
а) ![]() ; б) 4; в)
; б) 4; в) ![]() .
.
Вариант 4.
1.
Вычислите
площадь фигуры, ограниченной линиями: ![]() .
.
2. Выберите
правильный вариант ответа. Площадь фигуры, ограниченной
линиями ![]() , равна:
, равна:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Критерии оценки.
За каждый правильный ответ на контрольные вопросы – начисляется 0,5 балла.
За каждое правильно решенное задание – начисляется 4 балла.
Итого –10 баллов.
10 баллов оценка «5»
8-9 баллов оценка «4»
6-7 баллов оценка «3»
5 и менее оценка «2»
2.3 Самостоятельные работы
Цель проведения таких работ заключается в проверке уровня освоения изучаемого материала на учебном занятии. На выполнение самостоятельной работы (в зависимости от количества заданий) отводится 10- 20 минут. Во время выполнения самостоятельной работы обучающиеся могут пользоваться справочными материалами.
Самостоятельные работы по темам:
«Производная», «Преобразование выражений», «Вычисление производной с помощью определения», «Вычисление производных алгебраических функций», «Вычисление производных сложных функций», «Нахождение наибольшего и наименьшего значений функции», «Свойства функций», «Исследование функции и построение ее графика», «Вычисление первообразных функций», «Вычисление определенного интеграла», «Применение интеграла для вычисления площадей и объемов», «Тригонометрические функции углов поворота», «Преобразование тригонометрических выражений», «Решение тригонометрических уравнений», «Преобразование выражений», «Преобразование выражений, содержащих радикалы», «Решение иррациональных уравнений», «Преобразование выражений, содержащих степени с дробными показателями», «Преобразование выражений, содержащих степени и логарифмы», «Решение рациональных уравнений и неравенств», «Решение рациональных уравнений и неравенств», «Решение показательных уравнений и неравенств», «Решение логарифмических уравнений и неравенств», «Углы и расстояния в пространстве», «Двугранный угол», «Перпендикулярность прямой и плоскости», «Параллелепипед», «Призма», «Пирамида», «Цилиндр», «Конус», «Шар. Сфера», «Многогранники и тела вращения», «Элементы комбинаторики и теории вероятностей».
Оценка письменных самостоятельных работ осуществляется по тем же критериям, что имеются для контрольных работ, с учѐтом общих классификаций ошибок.
Примеры самостоятельных работ
Обучающая самостоятельная работа
Заполните пропуски в решении задачи №1и решите задачу№2.
Задача1 . Из точек А и В, лежащих в гранях
двугранного угла, опущены перпендикуляры
![]() и
и ![]() на ребро угла. Найдите
отрезок
на ребро угла. Найдите
отрезок
АВ,
если ![]() = 8
см,
= 8
см, ![]() = 5
см,
= 5
см, ![]() =10 см,
=10 см,
двугранный
угол равен 60![]() .
.
Р е ш е н и е.
1.
Проводим
![]() .
. ![]() - параллелограмм (по …),
следовательно,
- параллелограмм (по …),
следовательно, ![]() =5
см;
=5
см; ![]() = 10
см.
= 10
см.
2.
Прямая
![]() , так как …, значит,
, так как …, значит, ![]() . Следовательно,
. Следовательно, ![]() , в треугольнике АВМ
, в треугольнике АВМ
![]() , тогда
, тогда ![]() (по теореме …).
(по теореме …).
3.
![]() - линейный угол
двугранного угла
- линейный угол
двугранного угла ![]() (так
как …),
(так
как …), ![]()
В
треугольнике ![]() :
:
![]() (по теореме …);
(по теореме …); ![]() (см).
(см).
4.
Имеем
![]() (см).
(см).
О т в е т: ![]() см.
см.
Задача 2. Точки А и В лежат на ребре прямого двугранного угла. Отрезки АС и ВD проведены в разных гранях, перпендикулярно к ребру двугранного угла. АВ = а, AC = b, BD = c.
![]()
1. Объясните, как построить
линейный угол двугранного
угла.
2. Укажите различные способы
вычисления длины отрезка СD.
3. Найдите длину отрезка CD.
«Основные тригонометрические формулы»
1. Основное
тригонометрическое тождество ![]() выполняется
при любых значениях
выполняется
при любых значениях ![]() .
.
2. Упростите
выражения: а) ![]() ;
б)
;
б) ![]() .
.
3. Следствием
из основного тригонометрического тождества является формула, выражающая ![]() через
через ![]() :
: ![]() .
.
4. Найдите
значение тригонометрической функции ![]() , если известно, что
, если известно, что ![]() .
.
5. Тангенсом
угла ![]() называется отношение ...
угла
называется отношение ...
угла ![]() к
его ...:
к
его ...: ![]() .
.
6. Из
определения тангенса и котангенса следует: ![]() .
.
7. Соотношение
между тангенсом и косинусом одного и того же угла ![]() , когда
, когда ![]() .
.
8. Формула
![]() не имеет смысла при
не имеет смысла при ![]() .
.
9. Преобразуйте
выражения: а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() .
.
10. Упростите: а) ![]() ; б)
; б) ![]() .
.![]()
11. Докажите
тождество: ![]() .
.
Критерии оценки.
За каждый правильный ответ на вопросы 1,3, 5, 6,7,8 – начисляется 1 балл.
За правильно решенное задание – начисляется 2 балла.
Итого – 16 баллов.
15 – 16 баллов оценка «5»
12 – 14 баллов оценка «4»
9 – 11 баллов оценка «3»
8 и менее оценка «2»
Вычислите:
|
8 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
a |
b |
С |
d |
e |
f |
g |
h |
«Решение показательных уравнений»
Решите
уравнение: а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() .
.
2.4 Тестирование
Тестовая проверка знаний обучающихся предусматривает либо решение простейших заданий, либо ответы на вопросы. Тесты «закрытого типа» имеют один правильный вариант ответа из 4 предлагаемых вариантов. Время выполнения тестовых заданий от 10 до 25 минут. Задания выполняются после прохождения и закрепления материала. Задания обучающиеся выполняют на отдельных бланках в виде таблицы. Ниже таблицы пишутся, где нужны расчёты или формулы. В таблице две строки: 1)№ вопроса; 2)№ ответа. Виды проверки: самопроверка, взаимопроверка.
Оценка за тестовую работу выставляется по следующему алгоритму:
1. Определяется общее количество баллов за работу в целом.
2.Определяется количество набранных баллов за верные ответы.
3. Определяется коэффициент выполнения задания по формуле:
КВЗ=![]()
![]()
если КВЗ = 1 - выставляется оценка «отлично»;
если КВЗ от 0,8 до 1 - выставляется оценка «хорошо»;
при КВЗ от 0,6 до 0,8 - выставляется оценка «удовлетворительно»;
при КВЗ < 0,6 - выставляется оценка «неудовлетворительно».
Составлен сборник тестов по темам: «Производная», «Вычисление производной с помощью определения», «Вычисление производных алгебраических функций», «Вычисление производных сложных функций», «Нахождение наибольшего и наименьшего значений функции», «Свойства функций», «Вычисление первообразных функций», «Вычисление определенного интеграла», «Преобразование тригонометрических выражений», «Преобразование выражений, содержащих степени и логарифмы», «Углы и расстояния в пространстве», «Двугранный угол», «Прямые и плоскости в пространстве»«Перпендикулярность прямой и плоскости», «Параллелепипед», «Призма», «Пирамида», «Цилиндр», «Конус», «Шар. Сфера», «Многогранники и тела вращения», «Элементы комбинаторики и теории вероятностей».
«Тела вращения»
I вариант
1. Цилиндром называется тело, ограниченное поверхностью:
А. Конической. Б. Концентрической. В. Цилиндрической.
Г. Сферической.
2. Осевым сечением цилиндра является:
А. Треугольник. Б. Круг. В. Прямоугольник. Г. Трапеция.
3. Площадь боковой поверхности цилиндра определяется по формуле, где L – образующая, R – радиус, H – высота:
А.
![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
4. Назовите элемент, не принадлежащий конусу:
А. Образующая. Б. Ось. В. Высота. Г. Медиана.
5. Сфера является поверхностью:
А. Конуса. Б. Усеченного конуса. В. Цилиндра. Г. Шара.
6. Площадь поверхности сферы определяется по формуле, где R – радиус сферы:
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
7. Если высота конуса 15 см, а радиус основания 8 см, то образующая конуса равна:
А. 14 см. Б. 17 см. В. 13 см. Г. 6 см.
8. Секущая плоскость удалена от центра шара на расстояние 8 см, а радиус шара равен 10 см. Вычислите площадь сечения шара.
А. ![]() см
см![]() . Б.
. Б. ![]() см
см![]() . В.
. В. ![]() см
см![]() . Г.
. Г. ![]() см
см![]() .
.
9. Образующая конуса равна 10 см, а диаметр основания – 12 см. Вычислите площадь осевого сечения конуса.
А. 24 см![]() . Б. 12
см
. Б. 12
см![]() . В. 26
см
. В. 26
см![]() . Г. 48
см
. Г. 48
см![]() .
.
10. Высота цилиндра равна 10 см, а радиус его основания – 5 см. Плоскость пересекает цилиндр параллельно его оси и удалена от нее на 4 см. Вычислите площадь сечения.
А. 60 см![]() . Б. 50 см
. Б. 50 см![]() . В. 40 см
. В. 40 см![]() . Г. 30 см
. Г. 30 см![]() .
.
11. Образующая конуса равна 7 см, а высота – 6 см. Вычислите объем конуса.
А. ![]() см
см![]() . Б.
. Б. ![]() см
см![]() . В.
. В. ![]() см
см![]() . Г.
. Г. ![]() см
см![]() .
.
12. Равнобедренный треугольник с основанием 8 см и боковыми сторонами по 5 см вращается вокруг высоты, проведенной к основанию. Вычислите объем тела вращения.
А. ![]() см
см![]() . Б.
. Б. ![]() см
см![]() . В.
. В. ![]() см
см![]() . Г.
. Г. ![]() см
см![]() .
.
13. Проекцией тела в горизонтальной плоскости является круг, а в вертикальной плоскости – равнобедренный треугольник. Определите форму тела.
А. Цилиндр. Б. Пирамида. В. Конус. Г. Шар.
14. В цилиндрическую банку диаметром 10 см опустили в жидкость деталь. Вычислите объем детали, если высота жидкости в банке поднялась на 4 см.
А. ![]() см
см![]() . Б.
. Б. ![]() см
см![]() . В.
. В. ![]() см
см![]() . Г.
. Г. ![]() см
см![]() .
.
15. Ребро куба равно а. Вычислите радиус шара, описанного около куба.
А. а. Б. ![]() . В. 0,5а.
Г. 1,5а.
. В. 0,5а.
Г. 1,5а.
16. Сколько можно провести диаметров через точку, произвольно взятую внутри шара?
А. Одну. Б. Ни одной. В. Две. Г. Бесконечно много.
17. Прямоугольник со сторонами 5 см и 4 см вращается вокруг большей стороны. Вычислите объем тела вращения.
А. ![]() см
см![]() . Б.
. Б. ![]() см
см![]() . В.
. В. ![]() см
см![]() . Г.
. Г. ![]() см
см![]() .
.
18. Поверхности шаров относятся, как 4 : 9. А как относятся их диаметры?
А. 1 : 2. Б. 3 : 2. В. 2 : 3. Г. 3 : 4.
19. Радиус шара 1 м. Вычислите объем шара.
А. ![]() м
м![]() . Б.
. Б. ![]() м
м![]() . В.
. В. ![]() м
м![]() . Г.
. Г. ![]() м
м![]() .
.
20. Образующая
конуса равна 4 дм и наклонена к основанию под углом 60![]() . Вычислите площадь
боковой поверхности конуса.
. Вычислите площадь
боковой поверхности конуса.
А. ![]() см
см![]() . Б. 8
. Б. 8![]() см
см![]() . В. 6
. В. 6![]() см
см![]() . Г. 4
. Г. 4![]() см
см![]() .
.
21. Объем и площадь поверхности шара выражены одним и тем же числом. Вычислите радиус шара.
А. 3. Б. 4. В. 5. Г. 6.
22. В шар вписан прямоугольный параллелепипед с измерениями 6 см, 3 см и 2 см. Вычислите радиус шара.
А. 1,5 см. Б. 2 см. В. 3 см. Г. 3,5 см.
23. Диаметр цилиндра равен 6 см, а высота – 10 см. Вычислите площадь его боковой поверхности.
А. 30![]() см
см![]() . Б. 60
. Б. 60![]() см
см![]() . В. 20
. В. 20![]() см
см![]() . Г. 40
. Г. 40![]() см
см![]() .
.
24. Как изменится объем шара, если радиус увеличить в 2 раза?
А. Увеличится в 8 раз. Б. Не изменится. В. Увеличится в 4 раза.
Г. Увеличится в 2 раза.
25. Как называется отрезок, который получается в результате пересечения двух сечений шара?
А. Диаметр. Б. Радиус. В. Хорда. Г. Медиана.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
II вариант
1. Назовите элемент, не принадлежащий цилиндру:
А. Апофема. Б. Высота. В. Образующая. Г. Радиус.
2. Боковая поверхность конуса определяется по формуле, где L – образующая, R – радиус, H - высота:
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
3. Конус не может быть получен вращением:
А. Прямоугольника вокруг одной из сторон. Б. Равностороннего треугольника вокруг медианы. В. Прямоугольного треугольника вокруг одного из катетов. Г. Равнобедренного треугольника вокруг высоты.
4. Выявите формулу, не относящуюся к вычислению площади поверхности или объема конуса, где L – образующая, R – радиус, H – высота:
А.
![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
5. Сфера и плоскость не могут иметь:
А. Одну общую точку. Б. Ни одной общей точки. В. Две общие точки.
Г. Много общих точек.
6.
Объем
конуса определяется по формуле, где ![]() - площадь основания, H
– высота, R – радиус: А.
- площадь основания, H
– высота, R – радиус: А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
7. Шар и цилиндр имеют равные объемы, а диаметр шара равен диаметру основания цилиндра. Если выразить высоту цилиндра через радиус шара, то она будет равна:
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
8. Сколько осей симметрии у цилиндра?
А. Одна. Б. Ни одной. В. Две. Г. Бесчисленное множество.
9. Радиус шара 12 см. На касательной плоскости лежит точка К, которая удалена от точки касания на 5 см. На каком расстоянии находится точка К от поверхности шара? А. 1 см. Б. 2 см. В. 0,5 см. Г. 13 см.
10. Радиус основания конуса равен 6 см, а высота – 8 см. Вычислите его образующую.
А. 10 см. Б. 20 см. В. 15 см. Г. 25 см.
11. Образующая
конуса равна 12 см и наклонена к основанию под углом 30![]() . Вычислите высоту
конуса.
. Вычислите высоту
конуса.
А. 8 см. Б. 6 см. В. 10 см. Г. 4 см.
12. В горизонтальной и вертикальной плоскости проекциями тела являются круги. Определите форму тела.
А. Конус. Б. Цилиндр. В. Шар. Г. Усеченный конус.
13. Радиус цилиндра увеличили в два раза, а высоту уменьшили в два раза. Как изменится объем цилиндра?
А. Увеличится в 2 раза. Б. Уменьшится в 2 раза. В. Не изменится.
Г. Увеличится в 4 раза.
14. Прямоугольник со сторонами 6 см и 4 см вращается сначала вокруг меньшей стороны, а затем – большей. Одинаковы ли объемы тел вращения?
А. Да. Б. Нет.
15. Ребро куба равно а. Вычислите радиус шара, вписанного в куб.
А. а. Б. 2а. В. 0,5а. Г. 1,5а.
16. Площадь осевого сечения цилиндра равна S. Вычислите площадь боковой поверхности цилиндра.
А. 2S.
Б. 3S.
В. 3,5S. Г. ![]() .
.
17. Площадь
большого круга равна 1 м![]() .
Вычислите площадь поверхности шара.
.
Вычислите площадь поверхности шара.
А. 2 м![]() . Б. 3 м
. Б. 3 м![]() . В. 4 м
. В. 4 м![]() . Г. 5 м
. Г. 5 м![]() .
.
18. Высота равностороннего цилиндра равна 10 см. Вычислите его объем.
А. ![]() см
см![]() . Б.
. Б. ![]() см
см![]() . В.
. В. ![]() см
см![]() . Г.
. Г. ![]() см
см![]() .
.
19. Около прямоугольного параллелепипеда, измерения которого равны 2 см, 4 см и 4 см описана сфера. Вычислите площадь поверхности сферы.
А. ![]() см
см![]() . Б.
. Б. ![]() см
см![]() . В.
. В. ![]() см
см![]() . Г.
. Г. ![]() см
см![]() .
.
20. Через
середину высоты конуса и перпендикулярно ей построено сечение плоскостью.
Площадь сечения равна 8 см![]() .
Вычислите площадь основания конуса.
.
Вычислите площадь основания конуса.
А. 23 см![]() . Б. 32 см
. Б. 32 см![]() . В. 46 см
. В. 46 см![]() . Г. 64 см
. Г. 64 см![]() .
.
21. Как называется отрезок, который получается в результате пересечения двух больших кругов шара?
А. Диаметр. Б. Хорда. В. Радиус. Г. Апофема.
22. Образующая
конуса наклонена к основанию под углом 60![]() . Радиус основания конуса
r. Вычислите площадь боковой
поверхности конуса.
. Радиус основания конуса
r. Вычислите площадь боковой
поверхности конуса.
А.
![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
23. Высота равностороннего цилиндра равна 6 дм. Вычислите площадь боковой поверхности цилиндра.
А. 16![]() дм
дм![]() . Б. 26
. Б. 26![]() дм
дм![]() . В. 36
. В. 36![]() дм
дм![]() . Г. 6
. Г. 6![]() дм
дм![]() .
.
24. Как изменится площадь поверхности шара, если радиус увеличить в 3 раза?
А. Увеличится в 3 раза. Б. Не изменится. В. Увеличится в 9 раз. Г. Уменьшится в 9 раз.
25. На окраску шара диаметром 2 дм требуется 20 г краски. Сколько краски потребуется для окраски шара диаметром 6 дм?
А. 60 г. Б. 120 г. В. 180 г. Г. 240 г.
Критерии оценки.
За каждый правильный ответ на вопрос – начисляется 1 балл.
Итого – 25 баллов.
24 – 25 баллов оценка «5»
21 – 23 баллов оценка «4»
17 – 20 баллов оценка «3»
16 и менее оценка «2»
«Прямые и плоскости в пространстве»
Верно ли утверждение?
I. Углом между двумя пересекающимися прямыми называется угловая мера меньшего из образовавшихся между ними углов.
II.
Угол между параллельными прямыми равен 180![]() .
.
III.
Скрещивающиеся прямые называются перпендикулярными, если угол между ними равен
90![]() .
.
IV. Углом между прямой и плоскостью называется угол между этой прямой и перпендикуляром к плоскости.
Заполните пропуски.
I. Пересечение угла, образованного двумя плоскостями и плоскости,... к линии их пересечения, является углом между плоскостями.
1. Перпендикулярной.
2. Параллельной.
3. Наклонной.
II. Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно … данным скрещивающимся прямым.
1. Перпендикулярными.
2. Параллельными.
III. Угол между … плоскостями считается равным нулю.
1. Пересекающимися.
2. Перпендикулярными.
3. Параллельными.
IV.
Точка С отстоит от плоскости на расстояние 4
см. Длина наклонной, проведенной из этой точки под углом 45![]() к плоскости, равна …
к плоскости, равна …
1.![]() см. 2. 2
см. 3. 32 см. 4. 8 см.
см. 2. 2
см. 3. 32 см. 4. 8 см.
Верны ли следующие утверждения?
I. Если угол между
скрещивающимися прямыми 90![]() ,
то их нельзя назвать перпендикулярными.
,
то их нельзя назвать перпендикулярными.
II.
Наклонная равна 8 см. Проекция этой наклонной на плоскость равна ![]() см, если наклонная
составляет с плоскостью угол в 30
см, если наклонная
составляет с плоскостью угол в 30![]() .
.
Заполните пропуски.
I. Угол между параллельными плоскостями считается равным …
1. Нулю. 2. 180![]() . 3. 90
. 3. 90![]() .
.
II. Углом между двумя пересекающимися прямыми называют величину … из углов, определяемых этими прямыми.
1. Одного. 2. Меньшего. 3. Большего.
III. Угол между двумя пересекающимися плоскостями … от выбора секущей его плоскости, перпендикулярной линии пересечения данных плоскостей.
1. Не зависит. 2. Зависит.
IV.
Точка В отстоит от плоскости на расстояние 5
см. Длина наклонной проведенной из этой точки под углом 30![]() к плоскости, равна …
к плоскости, равна …
1. 5 см. 2. 2,5 см. 3. 10 см.
Верны ли следующие утверждения?
I. Углом между скрещивающимися прямыми называется угол между пересекающимися параллельными им прямыми.
II. Этот угол не зависит от того, какие взяты пересекающиеся прямые.
III. Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость.
IV.
Угол между параллельными прямой и плоскостью равен 180![]() .
.
Верно ли утверждение?
I. Угол между прямой и
плоскостью дополняет до 90![]() угол
между этой прямой и перпендикуляром к плоскости.
угол
между этой прямой и перпендикуляром к плоскости.
II.
Наклонная равна 7 см. проекция этой наклонной на плоскость равна ![]() см, если наклонная
составляет с плоскостью угол в 60
см, если наклонная
составляет с плоскостью угол в 60![]() .
.
Критерии оценки.
За каждый правильный ответ начисляется 1балл.
Итого – 10 баллов.
10 баллов оценка «5»
8-9 баллов оценка «4»
6-7 баллов оценка «3»
5 и менее оценка «2»
«Площадь поверхности призмы»
1.
Сторона
основания правильной шестиугольной призмы равна 6
см, а большая диагональ призмы образует с основанием угол, равный 30![]() . Площадь полной
поверхности призмы равна:
. Площадь полной
поверхности призмы равна:
а)
![]() см
см![]() ; б)
; б) ![]() см
см![]() ; в)
; в) ![]() см
см![]() ; г)
; г) ![]() см
см![]() .
.
2.
![]() - правильная треугольная
призма, сторона основания которой равна 4
см, боковое ребро равно 3 см, точки E
и F –
середины ребер
- правильная треугольная
призма, сторона основания которой равна 4
см, боковое ребро равно 3 см, точки E
и F –
середины ребер ![]() и
и
![]() . Площадь сечения призмы
плоскостью, проходящей через точки С, E
и F, равно:
. Площадь сечения призмы
плоскостью, проходящей через точки С, E
и F, равно:
а) ![]() см
см![]() ; б)
; б) ![]() см
см![]() ; в)
; в) ![]() см
см![]() ; г)
; г) ![]() см
см![]() .
.
Критерии оценки.
За каждый правильный ответ начисляется 5баллов.
Итого – 10 баллов.
10 баллов оценка «5»
8-9 баллов оценка «4»
6-7 баллов оценка «3»
5 и менее оценка «2»
«Пирамида»
1. Сделайте рисунок четырехугольной пирамиды, обозначьте ее и запишите: вершину, боковые ребра, основание, боковые грани.
2. Закончите предложение:
а) высотой пирамиды называется …;
б) пирамида называется правильной, если …;
в) усеченная пирамида – нижний многогранник, отсекаемый от пирамиды плоскостью, параллельной …;
г) апофемой правильной пирамиды называется …;
д) диагональное сечение пирамиды – сечение плоскостью, проходящей …
Критерии оценки.
За каждый правильный ответ в задании 1 начисляется 5баллов.
За каждый правильный ответ в задании 2 начисляется 5баллов.
Итого – 10 баллов.
10 баллов оценка «5»
8-9 баллов оценка «4»
6-7 баллов оценка «3»
5 и менее оценка «2»
2.5 Устный опрос и устные задания
Основой устного опроса являются пересказ конспекта или ответы на вопросы по изученной теме. Студенты отвечает у доски или с места. При фронтальном опросе – вопросы задаются всей группе, вызывается для краткого ответа тот или иной обучающийся, выстраивается беседа. Задания, выполняемые устно, являются упражнениями в вычислениях или тождественных преобразованиях. Время выполнения устных заданий от 15 до 10 минут. Под фронтальным устным заданием обычно понимают решение одного и того же задачи всеми студентами группы в одно и то же время. Задания выполняются после прохождения и закрепления материала. Имеются задания по всем разделам курса.
Оценка устных ответов
Оценка «5» ставится в том случае, если обучающийся:
1) обнаруживает полное понимание и знание математических теорий, умеет подтвердить их конкретными примерами, применить при выполнении практических заданий;
2) дает точные определения основных понятий, теорем, алгоритмов решения;
3) технически грамотно выполняет, чертежи, схемы, графики, сопутствующие ответу;
4)правильно записывает формулы, при объяснении математических теорий;
5)при ответе студент умеет отобрать главное, обнаруживает самостоятельность и аргументированность суждений, умеет установить связь между изучаемым и ранее изученным материалом по курсу математики;
6) умеет самостоятельно и рационально работать с учебником, дополнительной литературой и справочниками.
Оценка «4» ставится в том случае, если ответ удовлетворяет названным выше требованиям, но обучающийся:
1)допускает одну не грубую ошибку или не более двух недочетов и может их исправить самостоятельно, или при небольшой помощи преподавателя;
2) не обладает достаточными навыками работы со справочной литературой (например, студент умеет все найти, правильно ориентируется в справочниках, но работает медленно).
Оценка «3» ставится в том случае, если ответ удовлетворяет названным выше требованиям, но обучающийся:
1)обнаруживает отдельные пробелы в усвоении существенных вопросов курса математики, не препятствующие дальнейшему усвоению программного материала;
2)испытывает затруднения в применении знаний, необходимых для решения заданий различных типов;
3)отвечает неполно, в том числе и на вопросы преподавателя;
4)обнаруживает недостаточное понимание отдельных положений при воспроизведении текста учебника или конспекта, или отвечает неполно на вопросы преподавателя, допуская одну-две грубые ошибки.
Оценка «2» ставится в том случае, если студент:
1)не знает и не понимает значительную или основную часть программного материала в пределах поставленных вопросов;
2) имеет слабо сформулированные и неполные знания и не умеет применять их к решению конкретных заданий по образцу;
3)или при ответе допускает более двух грубых ошибок, которые не может исправить даже при помощи преподавателя.
Оценка «1» ставится в том случае, если ученик не может ответить ни на один из поставленных вопросов.
Форма опроса зависит от целей урока, подготовки группы к уроку.
Вопросы к устному опросу
Тема «Функция и её свойства»
1) Что называется функцией?
2) Что такое естественная область определения функции?
3) Какая функция называется четной, нечетной?
4) Как найти точки пересечения графика функции с осями координат?
5) Какая функция называется сложной? Приведите примеры сложных функций. 6) Сформулируйте признак возрастания (убывания) функции.
7) Сформулируйте признак максимума (минимума) функции.
8) Опишите схему исследования функции.
9) Что такое точка экстремума?
10) Что такое экстремум функции?
1. Ребро куба равно 4 см. Вычислите объем куба.
2. Измерения прямоугольного параллелепипеда равны 5 дм, 6 дм и 7 дм. Вычислите его объем.
3.
Площадь
поверхности куба равна 96 см![]() .
Вычислите его объем.
.
Вычислите его объем.
4.
Площадь
грани куба равна 9 дм![]() .
Вычислите его объем.
.
Вычислите его объем.
5.
Площадь
основания прямоугольного параллелепипеда равна 12 см![]() , а объем – 36 см
, а объем – 36 см![]() . Вычислите его высоту.
. Вычислите его высоту.
6. Как изменится объем прямоугольного параллелепипеда, если его измерения увеличить в два раза?
7.
Объем
куба равен 64 см![]() .
Вычислите площадь его поверхности.
.
Вычислите площадь его поверхности.
8. Можно ли пересечь куб плоскостью так, чтобы в сечении получился правильный треугольник?
9. Измерения прямоугольного параллелепипеда равны 4 см, 4 см и 2 см. Вычислите диагональ параллелепипеда.
10. Вычислите площадь поверхности куба, если его диагональ равна 6 см.
11. Ребро куба равно а. Вычислите площадь диагонального сечения.
12. В параллелепипеде длины ребер, исходящих из одной вершины, равны 5 см, 4 см и 3 см. Вычислите сумму длин всех ребер.
13. Как изменится площадь боковой поверхности прямоугольного параллелепипеда, если высоту его увеличить в 4 раза, а каждую из сторон основания уменьшить в 2 раза?
Критерии оценки.
За каждый правильный ответ устного задания – 1 балл.
Итого – 13 баллов.
13 баллов оценка «5»
10-12 баллов оценка «4»
7-9 баллов оценка «3»
6 и менее оценка «2»
УСТНЫЕ ЗАДАНИЯ ПО ТЕМЕ «ПИРАМИДА»
1. Проекцией тела в горизонтальной плоскости является квадрат с диагоналями, а в вертикальной – треугольник. Определите вид тела.
2. Пирамида имеет 10 многогранных углов. Сколько она имеет ребер?
3. В правильной n-угольной пирамиде все ребра равны. При каких значениях n это возможно?
4. У правильной треугольной пирамиды все ребра равны по 4 см. Вычислите площадь поверхности пирамиды.
5. Существует ли пирамида, у которой 18 плоских углов?
6. Какие фигуры получатся при построении диагонального сечения усеченной пирамиды?
7. Высота усеченной пирамиды равна 6 см, а соответственные стороны оснований относятся, как 1 : 3. Вычислите высоту полной пирамиды.
8. У пирамиды 10 ребер. Сколько у нее граней?
9.
В
пирамиде через середину высоты проведено сечение, параллельное основанию.
Площадь сечения равна 8 см![]() .
Вычислите площадь основания пирамиды.
.
Вычислите площадь основания пирамиды.
10. В основании пирамиды – прямоугольник со сторонами 6 см и 8 см, а каждое боковое ребро равно 13 см. Вычислите высоту пирамиды.
11. Боковые
грани пирамиды наклонены к основанию под углом 60![]() . В основании пирамиды –
квадрат со стороною а. Вычислите площадь боковой поверхности пирамиды.
. В основании пирамиды –
квадрат со стороною а. Вычислите площадь боковой поверхности пирамиды.
12. В правильной четырехугольной пирамиде высота равна 3 дм, а боковое ребро – 5 дм. Вычислите объем пирамиды.
Критерии оценки.
За каждый правильный ответ устного задания – 1 балл.
Итого – 12 баллов.
12 баллов оценка «5»
9-11 баллов оценка «4»
6-8 баллов оценка «3»
5 и менее оценка «2»
Вопросы к устному опросу
Тема «Функция и её свойства»
1) Что называется функцией?
2) Что такое естественная область определения функции?
3) Какая функция называется четной, нечетной?
4) Как найти точки пересечения графика функции с осями координат?
5) Какую точку называют критической (стационарной) точкой функции?
6) Сформулируйте признак возрастания (убывания) функции.
7) Сформулируйте признак максимума (минимума) функции.
8) Опишите схему исследования функции.
2.6 Письменный опрос
Письменный опрос выполняется фронтально. Рассчитан такой опрос на 10-15 минут от урока. Письменные работы проводятся в форме математического диктанта (презентации), ответов на вопросы. Индивидуально письменный опрос проводится для студентов, у которых есть речевые дефекты (плохо говорит), или если обучающийся стесняется отвечать публично. Письменный опрос по определениям, формулам и свойствам математических понятий проводится в конце изучения темы. Выполняется на раздаточном материале. Критерий оценивания: правильность, полнота и точность выполнения задания. Имеются задания по всем разделам курса.
Критерии оценки ответов студентов
Оценка за письменный опрос выставляется по следующему алгоритму:
1. Определяется общее количество баллов за работу в целом.
1. Определяется коэффициент усвоения по формуле:
КУ=![]()
![]()
если КУ > 0,9 — 1 - выставляется оценка «отлично»;
если КУ от 0,8 до 0,9 - выставляется оценка «хорошо»;
при КУ от 0,6 до 0,8 - выставляется оценка «удовлетворительно»;
при КУ < 0,6 - выставляется оценка «неудовлетворительно».
Пример математического
диктанта
«Основные понятия и аксиомы стереометрии»
|
ВАРИАНТ №1 |
ВАРИАНТ №2 |
|
|
Планиметрия – это раздел геометрии, изучающий … |
Стереометрия – это раздел геометрии, изучающий … |
|
|
Через любые три точки пространства, не принадлежащие одной прямой, проходит … |
Через любые две точки пространства проходит … |
|
|
Существует, по крайней мере, четыре точки, … |
Если две плоскости имеют общую точку, то … |
|
|
Для любой плоскости в пространстве существуют точки, ей … |
Для прямых и плоскостей в пространстве выполняются все … |
|
|
Основными понятиями стереометрии являются … |
Основными понятиями планиметрии являются … |
|
|
Для обозначения плоскости указываются … |
Для обозначения прямой указываются … |
|
|
Плоскость является идеализацией … |
Прямая является идеализацией … |
|
|
Через две точки пространства проходит … прямых. |
Через три точки пространства можно провести … прямых, если … |
|
|
|
||
|
«Свойства функций» |
||
|
Вопрос |
Ответ |
|
|
Что такое числовая функция? |
|
|
|
Что такое область определения? |
|
|
|
Что такое область значений функции? |
|
|
|
Дайте определение четной и нечетной функций. |
|
|
|
Сформулируйте определение функции, возрастающей (убывающей) на множестве R? |
|
|
|
Дайте определения точки максимума функции. |
|
|
|
Дайте определение точки минимума функции. |
|
|
|
Что такое экстремум функции? |
|
|
2.7 Индивидуальное собеседование
Собеседование – эта форма организации обучения, которая предполагает проведение индивидуальных бесед преподавателя с обучающимися. Целью этих бесед является выявление пробелов в знаниях. Индивидуальное собеседование позволяет оценить логику поиска ответа и применение логических цепочек при решении заданий. Индивидуальные собеседования проводятся в основном на консультациях. По итогам собеседования может выставляться оценка в журнал.
Составлены вопросы и задания по разделам: «Развитие понятия о числе», «Корни, степени и логарифмы», «Основы тригонометрии», «Функции, их свойства и графики», «Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции», «Начала математического анализа», «Уравнения и неравенства», «Комбинаторика, статистика и теория вероятностей», «Прямые и плоскости в пространстве», «Многогранники», «Тела и поверхности вращения», «Измерения в геометрии», «Координаты и векторы».
Порядок выполнения заданий
1.Внимательно прочитайте текст.
2.Четко формулируйте ответы на вопросы, соблюдайте логичность и последовательность.
3.Правильно выполните рисунки, чертежи, графики, сопутствующие ответу .
4.Проиллюстрировать теоретические знания конкретными примерами.
5.Выполнить задания обязательного уровня сложности по данной теме.
Критерии оценки ответов студентов
Ответ оценивается отметкой «5», если студент:
полно раскрыл содержание материала в объёме, предусмотренном программой и учебником;
изложил материал грамотным языком в определённой логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность используемых при ответе умений и навыков;
отвечал самостоятельно без наводящих вопросов преподавателя.
Возможны одна-две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию преподавателя.
Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на отметку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
допущены один-два недочёта при освещении основного содержания ответа, исправленные по замечанию преподавателя;
допущены ошибка или более двух недочётов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию преподавателя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала;
имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов преподавателя;
студент не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов преподавателя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
Примеры вопросов и заданий
1. Комплексные числа и действия над ними.
2. Корни и их свойства.
3. Степени и их свойства.
4. Логарифмы и их свойства.
5. Основные теоремы о пределах.
6. Непрерывность функции в точке и на промежутке.
7. Свойства непрерывных функций. Приращение аргумента. Приращение функции.
8. Производная функции.
9. Дифференциал функции.
10. Геометрический смысл производной.
11. Механический смысл производной.
12. Таблица производных.
13. Понятие сложной функции.
14. Производная сложной функции.
15. Схема исследования функции.
16. Дайте определение степени с натуральным, отрицательным и дробным показателями. Перечислите свойства степеней с рациональным показателем.
17. Первообразная. Неопределенный интеграл. Основные свойства неопределенного интеграла.
18. Определенный интеграл. Основные свойства определенного интеграла. Геометрический смысл определенного интеграла.
19. Методы вычисления определенных интегралов. Формула Ньютона-Лейбница.
20. Геометрические и физические приложения определенного интеграла.
21. Формулировка классического определения вероятности. Теоремы суммы и произведения вероятностей.
22. Перечислите свойства прямых и обратных тригонометрических функций.
23. Запишите формулы, с помощью которых решают простейшие тригонометрические уравнения.
24. Схема исследования функции с помощью производной.
25. Решите
систему уравнений: 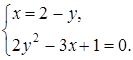
26. Решите
неравенство: 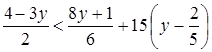 .
.
27. Решите
уравнение: (4x – 20)![]() ;
;
28. Вычислить
значение производной функции![]() . в точке
. в точке ![]() .
.
29. Найти
производную функции ![]() .
.
30. Найти
производную функции ![]() .
.
31. Найти
неопределенный интеграл ![]() .
.
32. Вычислить
определенный интеграл 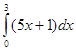 .
.
33. Вычислить
площадь фигуры, ограниченной линиями ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
34. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
35. Даны законы распределения дискретной случайной величины. Найдите математическое ожидание и дисперсию распределения дискретной случайной величины.
|
|
- 5 |
- 4 |
- 3 |
-2 |
0 |
1 |
2 |
|
Р |
|
|
|
|
|
|
|
2.8 Контрольные работы
Контрольная работа проводится в конце изучения раздела (темы). Цель проведения: оценить степень знаний и умений по крупной дидактической единице. На выполнение контрольной работы отводится 45 минут. Во время выполнения контрольной работы обучающиеся могут пользоваться справочными материалами, математическими таблицами.
Составлен сборник контрольных работ по разделам: «Развитие понятия о числе», «Корни, степени и логарифмы», «Основы тригонометрии», «Функции, их свойства и графики», «Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции», «Начала математического анализа», «Уравнения и неравенства», «Комбинаторика, статистика и теория вероятностей», «Прямые и плоскости в пространстве», «Многогранники», «Тела и поверхности вращения», «Измерения в геометрии», «Координаты и векторы».
Критерии оценивания контрольных работ по дисциплине.
При проведении контрольной работы уровень подготовки студента оценивается в баллах: 5(отлично), 4(хорошо), 3(удовлетворительно),
2 (неудовлетворительно).
1.Оценка «отлично» ставится за работу, выполненную полностью без ошибок и недочетов в строго заданной последовательности.
2. Оценка «хорошо» ставится за работу, выполненную полностью, но при наличии в ней не более одной негрубой ошибки и одного недочета или не более трех недочетов.
3. Оценка «удовлетворительно» ставится, если студент выполнил не менее 2/3 всей работы или допустил не более одной грубой ошибки или двух недочетов, не более одной грубой или одной негрубой ошибки, не более трех недочетов, наличии четырех, пяти недочетов.
4. Оценка «неудовлетворительно» ставится, если число ошибок или недочетов превысило норму для оценки «удовлетворительно» или правильно выполнено менее 2/3 всей работы.
5. Оценка «единица» ставится, если студент не выполнил ни одного задания.
Типичные ошибки
Грубые ошибки
1. Незнание основных понятий, определений, методов и приемов работы.
2. Неумение выполнять основные практические задания.
3. Отсутствие навыков работы со специальным оборудованием или несоблюдение техники безопасности.
4. Ответ, не раскрывающий содержания вопроса.
5. Неумение выделять в ответе главное.
6. Поверхностные знания без умения их применить и объяснить.
Негрубые ошибки
1. Неточность формулировок, определений, понятий.
2. Лексическая несочетаемость слов, стилевое нарушение в предложениях.
Недочеты
1. Лексические ошибки в конструировании текста в заданном стиле и жанре.
2. Небрежное выполнение записей, схем.
3. Орфографические и пунктуационные ошибки.
Примеры контрольных работ
ВХОДНОЙ КОНТРОЛЬ
I вариант
Часть I
Работа состоит из 3 частей (8 заданий). К заданиям необходимо записать верное решение и выбрать правильный вариант ответа(I часть).
1. Какое из данных чисел не
входит в область определения выражения ![]() ?
?
1) - 6; 2) 0; 3) 4; 4) 8.
|
|
|
|
![]() 1) (0;3);
2) (0;-3); 3) (0;3), (-3;6); 4) (3;0), (6;-3).
1) (0;3);
2) (0;-3); 3) (0;3), (-3;6); 4) (3;0), (6;-3).
3.
Чему равно значение выражения ![]() при а=
при а=![]() ?
?
1)
- 9; 2) - ![]() ; 3)
; 3) ![]() ; 4) 9.
; 4) 9.
4. График какой из функций изображен на рисунке?
|
1)
|
|
3) |
5. Решите неравенство: ![]()
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
Часть II
1.
Упростите выражение: ![]() .
.
2. Найдите значение выражения: ![]() .
.
Часть III
1.
Решите
уравнение: ![]() .
.
II вариант
Часть I
Работа состоит из 3 частей (8 заданий). К заданиям необходимо записать верное решение и выбрать правильный вариант ответа(I часть).
1.
Какое из данных чисел не входит в область определения выражения ![]() ?
?
1) 2; 2) 0; 3) -4; 4) -2.
![]()
|
2.
Решите систему уравнений |
|
|
1) (0;3); 2) (0;-3); 3) (0;-3), (3;0); 4) (-3;0), (0;3).
![]() 3.
Чему равно значение выражения
3.
Чему равно значение выражения ![]() при а=
при а=![]() ?
?
1)
- 4; 2) - ![]() ; 3)
; 3) ![]() ; 4) 4.
; 4) 4.
4. График какой из функций изображен на рисунке?
|
1)
|
|
3) |
5. Решите неравенство:
![]()
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
Часть II
1.
Упростите выражение: ![]() .
.
2.
Найдите значение выражения: ![]() .
.
Часть III
1.
Решите уравнение: ![]() .
.
Система оценивания работы.
За каждое верно решенное задание части I обучающийся получает 1 балл, части II обучающийся получает 2 балла, части III обучающийся получает 4 балла. Таким образом, максимальное число баллов, которое можно получить за верное решение всех заданий, равно 13. Оценка «3» ставится, если обучающийся набрал 5 – 6 баллов; оценка «4», если обучающийся набрал 7 – 9 баллов; оценка «5», если обучающийся набрал от 10 – 13 баллов.
Время на выполнение: 45 мин.
Глава 2 КОРНИ. СТЕПЕНИ. ЛОГАРИФМЫ
Контрольная работа № 1. «Корни, степени, логарифмы. Степенная, показательная, логарифмическая функции».
Работа состоит из 10 заданий. К заданиям необходимо записать верное решение.
I вариант
1. Вычислите:
а) ![]() ;б)
;б) 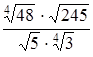 ;в) 251,5 +
;в) 251,5 + 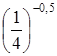 ;г)
;г) 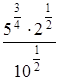 ;д) log0,518 + log0,5
;д) log0,518 + log0,5 ![]() 2 log0,5 3;е)
2 log0,5 3;е) ![]() ;ж)
;ж) 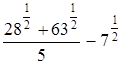 .
.
2. Укажите наименьшее значение функции на отрезке [0,5; 2].
а) y = ![]() ;б) y =
;б) y = ![]() ;в) y =
;в) y = ![]() .
.
3. Найдите область определения логарифмической функции
y = lg (x2 – x –12) + lg (x – 4).
II вариант
1. Вычислите:
а) ![]() ;б)
;б) 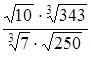 ;в) 27
;в) 27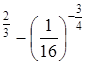 ;г)
;г) ![]() ;
;
д) log5 20 + log5 ![]() – 2 log5 5;
е)
– 2 log5 5;
е) ![]() ;
ж)
;
ж) 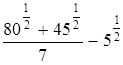 .
.
2. Укажите наименьшее значение функции на отрезке [1; 3].
а) y = ![]() ;б) y =
;б) y = ![]() ;в) y =
;в) y = ![]() .
.
3. Найдите область определения логарифмической функции
y = lg (x2 – x –2) + lg (x – 2).
Система оценивания работы.
За каждое верно решенное задание обучающийся получает 1балл. Таким образом, максимальное число баллов, которое можно получить за верное решение всех заданий, равно 10. Оценка «3» ставится, если обучающийся набрал 5-6 баллов; оценка «4», если обучающийся набрал 7-8 баллов; оценка «5», если обучающийся набрал 9- 10 баллов.
Время на выполнение: 45 мин.
3. Промежуточная аттестация
Экзаменационные материалы для промежуточной аттестации составляются с учетом требований к уровню подготовки обучающихся и рабочей программы по предмету.
В экзаменационную работу включены 10 заданий.
При проведении письменного экзамена по математике обучающимся предоставляется право использовать справочные таблицы по математике.
Оценка за письменный экзамен выставляется на основе анализа решения заданий обучающимся.
Требования к работам студентов:
работа выполнена в полном объеме с соблюдением необходимой последовательности заданий; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала); в решении нет ошибок в выкладках, рисунках, чертежах или графиках.
При проведении экзаменационной работы уровень подготовки студента оценивается в баллах: 5 (отлично), 4 (хорошо),
3 (удовлетворительно), 2 (неудовлетворительно).
1.Оценка «отлично» ставится за работу, выполненную полностью без ошибок и недочетов в строго заданной последовательности.
2. Оценка «хорошо» ставится за работу, выполненную полностью, но при наличии в ней не более одной негрубой ошибки и одного недочета или не более трех недочетов.
3. Оценка «удовлетворительно» ставится, если студент выполнил не менее 2/3 всей работы или допустил не более одной грубой ошибки или двух недочетов, не более одной грубой или одной негрубой ошибки, не более трех недочетов, наличии четырех, пяти недочетов.
4. Оценка «неудовлетворительно» ставится, если число ошибок или недочетов превысило норму для оценки «удовлетворительно» или правильно выполнено менее 2/3 всей работы
5. Оценка «единица» ставится, если студент не выполнил ни одного задания.
Примерная экзаменационная работа
I вариант
1.Вычислите:
251,5 + ![]() .
.
2.Решите
неравенство: ![]() .
.
3.Решите
уравнение: ![]() .
.
4. Найдите угловой
коэффициент касательной, проведенной к графику функции ![]() в его точке с абсциссой
в его точке с абсциссой ![]() .
.
5. Решите уравнения: ![]() .
.
6.
Постройте график функции у=![]() .
.
7
. Решите систему уравнений: ![]()
8.Стороны прямоугольника равны 2 дм и 4 дм. Вычислите полную поверхность фигуры, полученной при вращении прямоугольника вокруг его большей стороны.
9. Даны числа z1 = –2 + i, z2 = 2 – 3i. Вычислите сумму и произведение комплексных чисел z1и z2.
10. В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 10 очков.
II вариант
1.
Вычислите: 27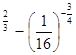 .
.
2.
Решите неравенство: ![]() .
.
3.Решите уравнение: ![]() .
.
4.Найдите угловой
коэффициент касательной, проведенной к графику функции ![]() в его точке с абсциссой
в его точке с абсциссой ![]() .
.
5. Решите уравнение: ![]() .
.
6.
Постройте график функции у=![]() .
.
7.Решите систему
уравнений: ![]()
8.Прямоугольник, стороны которого 15 см и 5 см, вращается вокруг меньшей стороны. Вычислите полную поверхность тела вращения.
9. Даны числа z1 = –3 + i, z2 = 1 – 4i. Вычислите сумму и произведение комплексных чисел z1и z2.
10. В случайном эксперименте монету бросили четыре раза. Какова вероятность того, что орел выпал ровно три раза?
Система оценивания работы.
Оценка «3» выставляется за любые 5 верно выполненных заданий.
Оценка «4» выставляется за любые 7 верно выполненных заданий. Оценка «5» выставляется за любые 9верно выполненных заданий.
Время на выполнение: 230 минут.
4. Методические указания для обучающихся с ограниченными возможностями здоровья
Обучающиеся из числа инвалидов и лиц с ограниченными возможностями здоровья имеют возможность изучать дисциплину по индивидуальному плану, согласованному с преподавателем и администрацией образовательного учреждения. Освоение дисциплины инвалидами и лицами с ограниченными возможностями здоровья осуществляется с использованием средств обучения общего и специального назначения. При освоении дисциплины инвалидами и лицами с ограниченными возможностями здоровья по индивидуальному плану предполагаются: изучение дисциплины с использованием информационных средств; индивидуальные консультации с преподавателем (разъяснение учебного материала и углубленное изучение материала), индивидуальная самостоятельная работа. В процессе обучения студентам из числа инвалидов и лиц с ограниченными возможностями здоровья информация предоставляется в формах, адаптированных к ограничениям их здоровья и восприятия информации:
Для лиц с нарушениями зрения:
– в печатной форме увеличенным шрифтом,
– в форме электронного документа (с возможностью увеличения шрифта).
В случае необходимости информация может быть представлена в форме аудиофайла.
Для лиц с нарушениями слуха:
– в печатной форме,
– в форме электронного документа.
Для лиц с нарушениями опорно-двигательного аппарата:
– в печатной форме,
– в форме электронного документа.
Данный перечень может быть конкретизирован в зависимости от контингента обучающихся. Индивидуальные консультации с преподавателем проводятся по отдельному расписанию, (в соответствии с индивидуальным графиком занятий обучающегося). Индивидуальная самостоятельная работа обучающихся проводится в соответствии с рабочей программой дисциплины и индивидуальным графиком занятий. Текущий контроль по дисциплине осуществляется в соответствии с фондом оценочных средств, в формах адаптированных к ограничениям здоровья и восприятия информации обучающихся.
Индивидуальные собеседования являются одним из методов учета знаний, умений и навыков обучающихся с ограниченными возможностями здоровья. Собеседование может проводиться во внеурочное время по вопросам устного опроса. Возможно, использование вопросов устного опроса для дистанционных заданий, которые могут быть выполнены в письменной форме. Продолжительность проведения индивидуального собеседования для указанной категории студентов увеличивается до 30 минут.
При оценивании устных ответов принимается во внимание:
- правильность ответа по содержанию, свидетельствующая об осознанности усвоения изученного материала;
- полнота ответа;
- умение практически применять свои знания.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.