Контрольно-оценочные материалы

Кировское областное государственное профессиональное
образовательное автономное учреждение
«Кировский технологический колледж пищевой промышленности»
Комплект контрольно-оценочных средств
по учебной дисциплине
ОП.01 МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ПРИКЛАДНЫХ ПРОФЕССИОНАЛЬНЫХ ЗАДАЧ
основной профессиональной образовательной программы
21.02.19 Землеустройство
|
Специалист по землеустройству |
|
квалификация |
Киров, 2023 г.
|
|
Комплект контрольно-оценочных средств разработан в соответствии с требованиями ФГОС среднего профессионального образования по профессии/специальности 21.02.19 Землеустройство, с учетом Рабочей программы воспитания по 21.02.19 Землеустройство |
|
Рассмотрено на заседании ПЦК
___________________________ Протокол № _ от «___» ______________202_ г.
Председатель ПЦК__________-
|
Утверждаю
Зам. директора по УМР __________________Я. В. Снигирева
от «___»________________202_ г.
|
Организация-разработчик: КОГПОАУ «Кировский технологический колледж пищевой промышленности
Составители/составитель:
Н. С. Никонова – преподаватель Кировского технологического колледжа пищевой промышленности
СОДЕРЖАНИЕ
1. Паспорт комплекта контрольно-оценочных средств.................................................. 4
2. Результаты освоения учебной дисциплины, подлежащие проверке....................... 5
3. Оценка освоения учебной дисциплины.......................................................................... 7
3.1. Формы и методы оценивания................................................................................... 7
3.2. Типовые задания для оценки освоения учебной дисциплины.......................... 9
4. Контрольно-измерительные материалы для итоговой аттестации по учебной дисциплине..................................................................................................................................................... 19
1. Паспорт комплекта контрольно-оценочных средств
В результате освоения учебной дисциплины вписать ОП.01 МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ПРИКЛАДНЫХ ПРОФЕССИОНАЛЬНЫХ ЗАДАЧ обучающийся должен обладать предусмотренными ФГОС СПО по специальности 21.02.19 Землеустройство, следующими умениями, знаниями, которые формируют профессиональную компетенцию, а также общими компетенциями и личностными результатами реализации программы воспитания:
Умения:
У 1. распознавать и анализировать задачу и/или проблему в профессиональном и/или социальном контексте выделять её составные части и определять этапы решения задачи
У 2. определять необходимые ресурсы и источники информации
У 3. использовать цифровые средства для решения профессиональных задач
У 4. применять современную научную профессиональную терминологию, определять и выстраивать траектории профессионального развития и самообразования
Знания:
З 1. значение математики в профессиональной деятельности;
З 2. основные математические методы решения прикладных задач в области профессиональной деятельности;
З 3. основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
З 4. основы интегрального и дифференциального исчисления.
Профессиональные компетенции (ПК)
ПК 1. 1. Выполнять полевые геодезические работы на производственном участке.
ПК 1. 2. Выполнять топографические съемки различных масштабов.
ПК 1. 3. Выполнять графические работы по составлению картографических материалов.
ПК 1. 4. Выполнять кадастровые съемки и кадастровые работы по формированию земельных участков.
ПК 1. 5. Выполнять дешифрирование аэро- и космических снимков для получения информации об объектах недвижимости.
ПК 1. 6. Применять аппаратно-программные средства для расчетов и составления топографических, межевых планов.
ПК 2. 1. Проводить техническую инвентаризацию объектов недвижимости.
ПК 2. 2. Выполнять градостроительную оценку территории поселения.
ПК 2. 3. Составлять технический план объектов капитального строительства с применением аппаратно-программных средств.
ПК 2. 4. Вносить данные в реестры информационных систем различного назначения.
ПК 3. 1. Консультировать по вопросам регистрации прав на объекты недвижимости и предоставления сведений, содержащихся в Едином государственном реестре недвижимости (далее - ЕГРН).
ПК 3. 2. Осуществлять документационное сопровождение в сфере кадастрового учета и (или) государственной регистрации прав на объекты недвижимости.
ПК 3. 3. Использовать информационную систему, предназначенную для ведения ЕГРН;
ПК 3. 4. Осуществлять сбор, систематизацию и накопление информации, необходимой для определения кадастровой стоимости объектов недвижимости.
ПК 4. 1. Проводить проверки и обследования для обеспечения соблюдения требований законодательства Российской Федерации.
ПК 4. 2. Проводить количественный и качественный учет земель, принимать участие в их инвентаризации и мониторинге.
ПК 4. 3. Осуществлять контроль использования и охраны земельных ресурсов.
ПК 4. 4. Разрабатывать природоохранные мероприятия.
Общие компетенции (ОК)
ОК 1. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам
ОК 2. Использовать современные средства поиска, анализа и интерпретации информации, и информационные технологии для выполнения задач профессиональной деятельности
ОК 3. Планировать и реализовывать собственное профессиональное и личностное развитие, предпринимательскую деятельность в профессиональной сфере, использовать знания по правовой и финансовой грамотности в различных жизненных ситуациях
Личностные результаты:
ЛР 4 Проявляющий и демонстрирующий уважение к труду человека, осознающий ценность собственного труда и труда других людей. Экономически активный, ориентированный на осознанный выбор сферы профессиональной деятельности с учетом личных жизненных планов, потребностей своей семьи, российского общества. Выражающий осознанную готовность к получению профессионального образования, к непрерывному образованию в течение жизни. Демонстрирующий позитивное отношение к регулированию трудовых отношений. Ориентированный на самообразование и профессиональную переподготовку в условиях смены технологического уклада и сопутствующих социальных перемен. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа»
ЛР 6 Ориентированный на профессиональные достижения, деятельно выражающий познавательные интересы с учетом своих способностей, образовательного и профессионального маршрута, выбранной квалификации
ЛР14 Проявляющий сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности
ЛР 22 Проявляющий осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению, мировоззрению, культуре, языку, вере, гражданской позиции, к истории, культуре, религии, традициям, языкам, ценностям народов Вятского края; готов и способен вести диалог с другими людьми и достигать в нем взаимопонимания
ЛР 26 Готовность обучающегося соответствовать ожиданиям работодателей: ответственный сотрудник, дисциплинированный, трудолюбивый, нацеленный на достижение поставленных задач, эффективно взаимодействующий с членами команды, сотрудничающий с другими людьми, проектно-мыслящий.
Формой аттестации по учебной дисциплине является зачет
2. Результаты освоения учебной дисциплины, подлежащие проверке
2.1. В результате аттестации по учебной дисциплине осуществляется комплексная проверка следующих умений и знаний, а также динамика формирования общих и профессиональных компетенций:
Таблица 1.1
|
Результаты обучения: умения, знания и общие |
Показатели оценки результата |
Форма контроля и оценивания |
|
Уметь: |
|
|
|
У 1. распознавать и анализировать задачу и/или проблему в профессиональном и/или социальном контексте выделять её составные части и определять этапы решения задачи |
умеет решать прикладные задачи в области профессиональной деятельности: решает задачи математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики, интегрального и дифференциального исчисления. Применяет метод Крамера и Гаусса при решении систем линейных уравнений; вычисление радианной меры угла, поворот точки вокруг начала координат, определение синуса, косинуса и тангенса угла. |
- оценка качества знаний при выполнении студентами практических работ; - анализ выполнения домашних заданий; - наблюдение и анализ деятельности студентов в процессе выполнения аудиторных заданий; - оценка качества знаний при сдаче зачета. |
|
У 2. определять необходимые ресурсы и источники информации |
||
|
У 3. использовать цифровые средства для решения профессиональных задач |
||
|
У 4. применять современную научную профессиональную терминологию, определять и выстраивать траектории профессионального развития и самообразования |
||
|
Знать: |
|
|
|
З 1. значение математики в профессиональной деятельности; |
обосновывает значение математики в профессиональной деятельности и при освоении ППССЗ; демонстрирует знания основных методов решения задач; демонстрирует знания основных понятий и методов математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; - демонстрирует знания основ интегрального и дифференциального исчисления. |
- оценка качества знаний при выполнении студентами практических работ; - анализ выполнения домашних заданий; наблюдение и анализ деятельности студентов в процессе выполнения аудиторных и внеаудиторных заданий; - оценка качества знаний при сдаче зачета. |
|
З 2. основные математические методы решения прикладных задач в области профессиональной деятельности; |
||
|
З 3. основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; |
||
|
З 4. основы интегрального и дифференциального исчисления |
3. Оценка освоения учебной дисциплины:
3.1. Формы и методы оценивания
Предметом оценки служат умения и знания, предусмотренные ФГОС ОП.01 МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ПРИКЛАДНЫХ ПРОФЕССИОНАЛЬНЫХ ЗАДАЧ, направленные на формирование общих и профессиональных компетенций.
Контроль и оценка освоения учебной дисциплины по темам (разделам) Таблица 2.2
|
Элемент учебной дисциплины |
Формы и методы контроля
|
|||||
|
Текущий контроль |
Рубежный контроль |
Промежуточная аттестация |
||||
|
Форма контроля |
Проверяемые У, З, ОК, ЛР |
Форма контроля |
Проверяемые ОК, У, З |
Форма контроля |
Проверяемые ОК, У, З |
|
|
Семестр |
|
|
|
|
Зачет |
У1, У2, У3, У4 З1, З2, З3, З4, ПК 1.1. – 1.6, ПК 2.1. – 2.4, ПК 3.1. – 3.4, ПК 4.1. – 4.4, ОК 01, ОК 02, ОК 03, ЛР4, ЛР 6, ЛР 14, ЛР 22, ЛР 26 |
|
Раздел 1 |
Устный опрос Практическое занятие 1 «Действия над матрицами» Практическое занятие 2 «Решение систем уравнений методами Крамера, Гаусса, методом обратной матрицы»
|
У1, У2, У3, У4 З1, З2, З3, З4, ПК 1.1. – 1.6, ПК 2.1. – 2.4, ПК 3.1. – 3.4, ПК 4.1. – 4.4, ОК 01, ОК 02, ОК 03, ЛР4, ЛР 6, ЛР 14, ЛР 22, ЛР 26 |
|
|
||
|
Раздел 2 |
Устный опрос Практическое занятие 3 «Задачи на составление уравнений и построение прямых и плоскостей» Практическое занятие 4 «Нахождение параметров кривых второго порядка. Построение кривых второго порядка» |
У1, У2, У3, У4 З1, З2, З3, З4, ПК 1.1. – 1.6, ПК 2.1. – 2.4, ПК 3.1. – 3.4, ПК 4.1. – 4.4, ОК 01, ОК 02, ОК 03, ЛР4, ЛР 6, ЛР 14, ЛР 22, ЛР 26 |
|
|
||
|
Раздел 3 |
Устный опрос Практическое занятие 5 «Действия с комплексными числами, записанными в различных формах. Решение уравнений» |
У1, У2, У3, У4 З1, З2, З3, З4, ПК 1.1. – 1.6, ПК 2.1. – 2.4, ПК 3.1. – 3.4, ПК 4.1. – 4.4. , ОК 01, ОК 02, ОК 03, ЛР4, ЛР 6, ЛР 14, ЛР 22, ЛР 26 |
|
|
||
|
Раздел 4 |
Устный опрос Практическое занятие 6 «Раскрытие неопределенностей» Практическое занятие 7 «Вычисление производных, исследование функции» Практическое занятие 8 «Вычисление приближенных значений функции. Оценка погрешности» Практическое занятие 9 «Приложения определенного интеграла» |
У1, У2, У3, У4 З1, З2, З3, З4, ПК 1.1. – 1.6, ПК 2.1. – 2.4, ПК 3.1. – 3.4, ПК 4.1. – 4.4, ОК 01, ОК 02, ОК 03, ЛР4, ЛР 6, ЛР 14, ЛР 22, ЛР 26 |
|
|
||
|
Раздел 5 |
Устный опрос Практическое занятие 10 «Вычисление вероятностей случайных событий» Практическое занятие 11 «Анализ, обработка и графическое предоставление данных» |
У1, У2, У3, У4 З1, З2, З3, З4, ПК 1.1. – 1.6, ПК 2.1. – 2.4, ПК 3.1. – 3.4, ПК 4.1. – 4.4, ОК 01, ОК 02, ОК 03, ЛР4, ЛР 6, ЛР 14, ЛР 22, ЛР 26 |
|
|
||
|
Раздел 6 6 |
Устный опрос
Самостоятельная работа |
У1, У2, У3, У4 З1, З2, З3, З4, ПК 1.1. – 1.6, ПК 2.1. – 2.4, ПК 3.1. – 3.4, ПК 4.1. – 4.4, ОК 01, ОК 02, ОК 03, ЛР4, ЛР 6, ЛР 14, ЛР 22, ЛР 26 |
||||
3.2. Типовые задания для оценки освоения учебной дисциплины
3.2.1. Типовые задания для оценки знаний
Практическое занятие 1
Тема: «Действия над матрицами»
Цель
- изучить понятие матриц, виды матриц, их роль в экономике и профессиональной деятельности;
- научится выполнять действия над матрицами: сложение, вычитание, умножение на число, умножение матриц
Основная задача – сформировать знания и умения при работе с матрицами
Указания: выполнять работу по алгоритму
Вопросы практической работы: алгоритм арифметических действий с матрицами. Область применения матриц в профессиональной деятельности
Свойства операций сложения и умножения:
1. A + B = B + A,
2. (A + B) + C = A + (B + C),
3. α(A + B) = αA + αB,
4. A(B + C) = AB + AC,
5. (A + B)C = AC + BC,
6. C(AB) = (CA)B,
7. α(AB) = (αA)B = A(αB).
 Операции над
матрицами
Операции над
матрицами
Пример. α = −3,
![]() .
.
Решение:
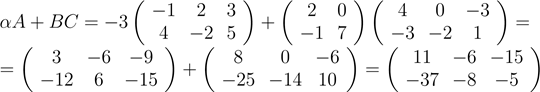
Задачи.
1. Элементами прямоугольной матрицы A3×4 являются числа aij = (i+j)2, где i = 1,2,3;j = 1,2,3,4. Требуется составить матрицы A и AT.
2. Найти линейные комбинации C = αA + βB матриц A и B:
a) ![]() 2;
2;
b) ![]() 2;
2;
c) 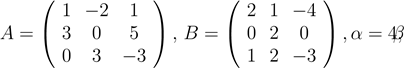 =
2;
=
2;
d) 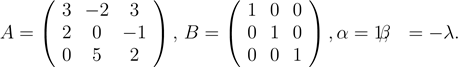
3. Решить уравнения:
a) ![]()
b) 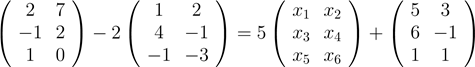 ;
;
c) ![]()
4. Вычислить произведения матриц:
a)
![]() ;
;
b) ![]() ;
;
c)
![]() ;
;
d) 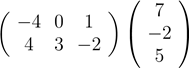 ;
;
e)
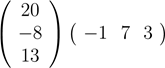 ;
;
f)
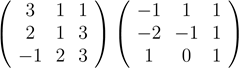 .
.
Практическое занятие 2
Тема: «Решение систем уравнений методами Крамера, Гаусса, методом обратной матрицы»
Цель
- изучить приемы решения систем линейных уравнений с тремя (и более) неизвестными;
- научится выполнять нахождение неизвестных методом Крамера и Гаусса
Основная задача – сформировать знания и умения при работе с определителями и расширенными матрицами
Указания: выполнять работу по алгоритму
Вопросы практической работы: алгоритм арифметических действий по методу Крамера и методу Гаусса. Область применения систем линейных уравнений в профессиональной деятельности
Если в в системе линейных уравнений число уравнений и неизвестных совпадает (m = n) и матрица A невырожденная, то решение этой системы может быть найдено по формулам Крамера.
Пусть ∆ — определитель системы, а ∆j —
определитель полученный из определителя системы заменой столбца с номером j на столбец свободных членов
уравнений. Тогда![]() , где j
= 1,2,...,n.
, где j
= 1,2,...,n.
Пример. Решить систему уравнений по формулам Крамера:
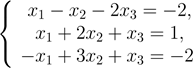 ,
,
Решение. Найдем определитель системы:
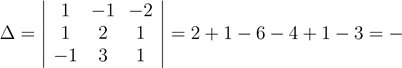 9;
9;
Найдем определители ∆j:
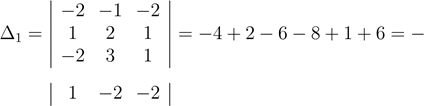 9;
9;
![]() 2
+ 2 + 2 = 9;
2
+ 2 + 2 = 9;
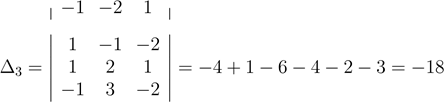 .
.
Получаем![]() .
.
Основной теоретический материал.
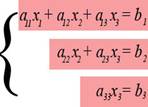 Метод
Гаусса, называемый также методом последовательного исключения неизвестных,
состоит в том, что при помощи элементарных преобразований систему линейных
уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к
трапециевидной (см. рисунок).
Метод
Гаусса, называемый также методом последовательного исключения неизвестных,
состоит в том, что при помощи элементарных преобразований систему линейных
уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к
трапециевидной (см. рисунок).
Рассмотрим алгоритм решения методом Гаусса на конкретном примере.
Решить
систему линейных уравнений 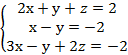
Применим прямой ход – получим нули под главной диагональю. Для этого:
Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду.
Вначале поменяем первую и вторую строку,
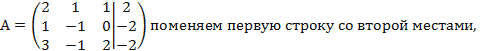
![]()
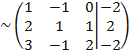
Выполним преобразования, благодаря которым получим нули под главной диагональю в первом столбце.
Для этого от второй строки отнимаем две первых, от третьей - три первых:
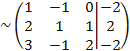
Т.е. каждый элемент первой строки мы умножаем на 2 и вычитаем из соответствующих элементов второй строки
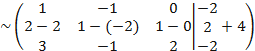
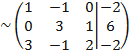
Каждый элемент первой строки умножаем на 3 и вычитаем из соответствующих элементов третьей строки
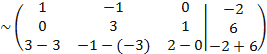
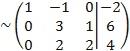 , таким образом получили новую матрицу.
, таким образом получили новую матрицу.

Все элементы третьей строки делим на два 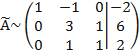
Выполним преобразования, благодаря которым получим нули во втором столбце под главной диагональю.
Для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
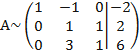
От третьей строки отнимаем вторую, умноженную на 3:
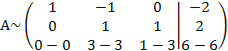 получаем новый вид А
получаем новый вид А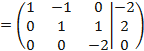
Разделим
третью строку на (-2), получаем: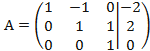
Проведем теперь обратный ход, то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца.
Надо
обнулить элемент ![]() , для этого от второй строки отнимем третью:
, для этого от второй строки отнимем третью:
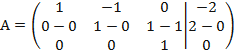 получаем
получаем 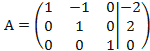
Далее обнуляем недиагональные элементы второго столбца а12, к первой строке прибавляем
вторую: 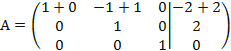 получаем
получаем  приведем к
приведем к
неизвестным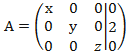 таким образом, полученной матрице соответствует система
таким образом, полученной матрице соответствует система
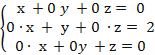 отсюда следует
отсюда следует ![]() Ответ:
(2,4,0)
Ответ:
(2,4,0)
Практическое занятие 3
Тема: «Задачи на составление уравнений и построение прямых и плоскостей»
Цель
- изучить алгебраическое описание прямой линии с помощью уравнения прямой;
- научится составлять уравнения и осуществлять построение прямых и плоскостей
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию, воспитание трудолюбия, усердия в достижении цели
Основная задача – сформировать знания и умения при работе с прямыми и плоскостями
Указания: выполнять работу по алгоритму
Вопросы практической работы: Уравнение прямой на плоскости - определение. Общее уравнение прямой. Уравнение прямой в отрезках. Уравнение прямой с угловым коэффициентом. Каноническое уравнение прямой на плоскости. Параметрические уравнения прямой на плоскости. Нормальное уравнение прямой. Область применения уравнений прямых и плоскостей в профессиональной деятельности.
Общее уравнение плоскости:
Общее уравнение плоскости имеет вид Ax+By+Cz+D=0, где коэффициенты A, B, C, D одновременно не равны нулю.
Уравнение плоскости по точке и направляющему вектору: Если известна некоторая точка, принадлежащая плоскости, и вектор n, перпендикулярный этой плоскости (который называют вектором нормали к плоскости), то уравнение данной плоскости можно составить по формуле:
A(x-х0)+B(y-у0)+C(z-z0)=0
Уравнение поверхности сферы:
Сфера радиуса R с центром в начале координат представлена уравнением второй степени. x2+y2+z2=R2 (R – радиус сферы)
Сфера радиуса R центр которой не совпадает с началом координат представлена другим уравнением второй степени.
(x−a)2+(y−b)2+(z−c)2=R2 (R - радиус сферы; a, b, c - смещение центра сферы относительно центра координат)
Задания для практической работы:
1. Составить уравнение сферы радиуса R = 5 с центром в начале координат.
2. Найти центр и радиус сферы (х+ 4)2+ (y —3)2+ z2=100.
3. Написать уравнение сферы с центром в точке С (2; —3; 5) и радиусом, равным 6.
4. Составить уравнение прямой по точке и направляющему вектору М (4, -2), n (3,2)
5. Составить уравнение плоскости по точке Р (4, -2; -1) и вектору нормали, n (-5;3,-2)
6. Доказать, что уравнение х 2+ у 2+ z 2—2х+ 4у—6z+ 5 = 0, является уравнением сферы.
7. Найти уравнение прямой, проходящей через две точки: (-1, 2) и (2, 1).
8. Составить уравнение плоскости, проходящей через точку А и перпендикулярной вектору ВС, если А(-4; 2; -1), В(1; 2;-1), С(-2; 0; 1).
Практическое занятие 4
Тема: «Нахождение параметров кривых второго порядка. Построение кривых второго порядка»
Цель
- изучить понятие о кривых второго порядка;
- научится строить кривые второго порядка, находить эксцентриситет, фокусы
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию, раскрыв основные идеи математического моделирования
Основная задача – сформировать знания и умения при работе с прямыми и плоскостями
Указания: выполнять работу по алгоритму
Вопросы практической работы: Уравнение прямой на плоскости - определение. Общее уравнение прямой. Уравнение прямой в отрезках. Уравнение прямой с угловым коэффициентом. Каноническое уравнение прямой на плоскости. Параметрические уравнения прямой на плоскости. Нормальное уравнение прямой. Область применения кривых второго порядка в профессиональной деятельности.
Построение кривых второго порядка.
К кривым второго порядка относят кривые, записанные уравнением Ах2 + Вху + Су2 + Ех + Ду + F = 0. В зависимости от значений коэффициентов (вещественные числа) это могут быть окружность, эллипс, гипербола, парабола. Эти кривые были известны с глубокой древности. Все эти кривые суть сечения прямого кругового конуса плоскостями (конические сечения).
Эллипс.
Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек F1 и F2 (фокусов) есть величина постоянная 2а, большая F1F2. Каноническое уравнение (простейшее) уравнение эллипса: х2/а2 + у2/в2 =1
Эллипс, заданный таким уравнением симметричен относительно осей координат (рис 1)
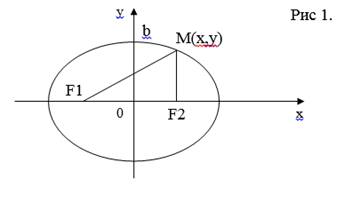
М (х,у) – произвольная точка эллипса, (х,у) – текущие координаты этой точки. Все точки эллипса удовлетворяют условию: F1M + F2M=2a.
а,в называются полуосями эллипса, а –
большая полуось, в – малая полуось. F1 и F2 – фокусы эллипса находятся на оси ох на
расстоянии С= ![]() 2 – в2)
от центра О. Отношение с/а = Е называется эксцентриситетом эллипса.
2 – в2)
от центра О. Отношение с/а = Е называется эксцентриситетом эллипса.
Пример 1.
1) Написать уравнение эллипса, если а=4, в=3;
2) Найти координаты фокусов;
3) Найти Е.
Ответ: 1) х2/16 + у2/9=1; 2)
С= ![]() =
= ![]() ,
F1 (-
,
F1 (- ![]() ,
0); F2 (
,
0); F2 ( ![]() ,
0); 3)Е = с/а =
,
0); 3)Е = с/а = ![]() /4 < 1.
/4 < 1.
Гипербола.
Гиперболой называется геометрическое место точек, разность расстояний каждой из которых до двух данных точек F1 и F2 (фокусов) есть постоянная величина 2а (0<2a<F1, F2).
Каноническое (простейшее) уравнение гиперболы.
Х2 /а2 – у2/в2 = 1
Гипербола, заданная уравнением
симметрична относительно осей координат (Рис 2). Она пересекает ось ох в точках
А1( -а, 0) и А2(+а, 0) – вершинах гиперболы и не
пересекает ось оу. Параметр а называется вещественной полуосью, в – мнимой
полуосью, С=![]() (а2 +в2)
- расстояние от фокуса до центра симметрии О. Отношение с/а=Е называется
эксцентриситетом гиперболы. Прямые у= ±в/а х называются асимптотами гиперболы.
(а2 +в2)
- расстояние от фокуса до центра симметрии О. Отношение с/а=Е называется
эксцентриситетом гиперболы. Прямые у= ±в/а х называются асимптотами гиперболы.
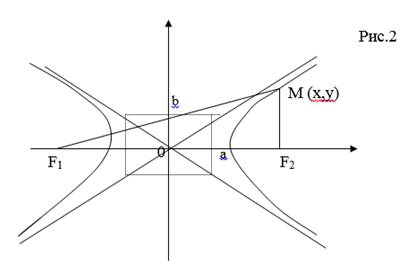
М(х,у) – произвольные точки гиперболы, (х,у) – текущие координаты произвольной точки. Все точки гиперболы удовлетворяют условию
│F1M-F2M│=2a.
Пример 2.
Дана гипербола х²-4у²=16.
1)Написать каноническое уравнение гиперболы;
2)Найти вещественную и мнимую полуоси;
3) Найти асимптоты гиперболы;
4) Вычислить эксцентриситет Е.
Ответ: 1)х²/16 - у²/4 = 1; 2) а=![]() = 4; в=
= 4; в=![]() =
2. 3) у = ±(в/а) х или у = ±(2/4)х или у = ±(1/2)х; 4) с=
=
2. 3) у = ±(в/а) х или у = ±(2/4)х или у = ±(1/2)х; 4) с= ![]() (а² + в²) =
(а² + в²) = ![]() =
= ![]() =
2
=
2![]() ,
,
Е=с/а=(2![]() )/4 = (
)/4 = (![]() )/2 ;
)/2 ;
Е=(![]() )/2
>1.
)/2
>1.
Парабола.
Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
Каноническое уравнение параболы имеет два вида:
1) у²= 2рх – парабола симметрична относительно ох (рис.3)
2) х²= 2ру – парабола симметрична относительно оу (рис.4)
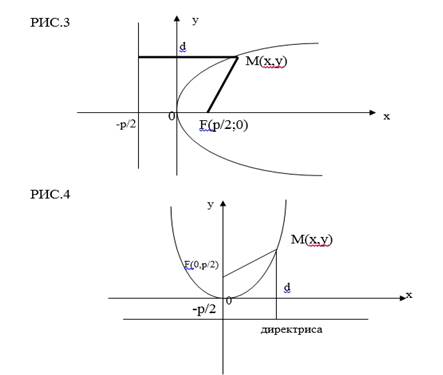
М (х,у) – произвольная точка парабола,
(х,у) – текущие координаты произвольной точки,
х = -р/2 – уравнение директрисы.
FM = d, где d – расстояние от точки М до директрисы.
В обоих случаях вершина параболы находится на оси симметрии в начале координат 0.
Парабола у² = 2рх имеет фокус F (р/2) и директрису х = - р/2
Парабола х = 2ру имеет фокус F (р/2) и директрису у = - р/2
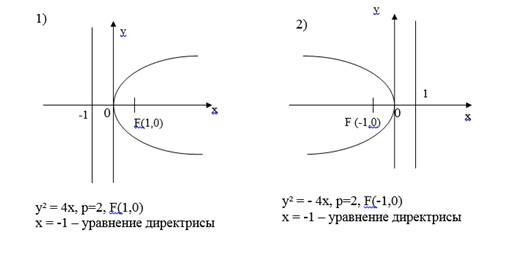
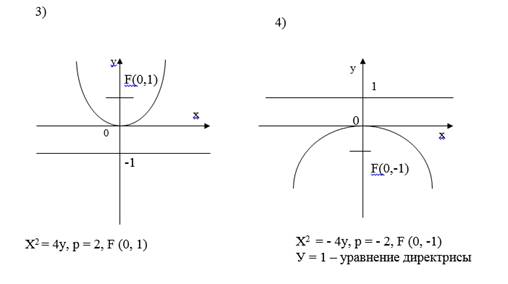
Пример 3.
Построить параболы заданные уравнениями:
1) у² = 4х;
2) у² = -4х;
3) х² =4у;
4) х² =-4у; а так же их фокусы и директрисы и написать уравнения директрис.
Ответ:
Окружность.
Уравнение окружности с центром в точке А (а,в) и радиусом R; (рис.6)
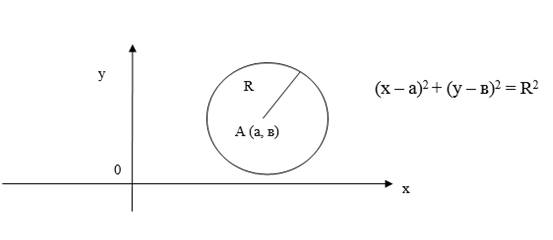
Пример 4.
1) Написать уравнение окружности с центром в точке А ( -1, 2), R = 2.
2) Построить ее.
3) Лежит ли точка О (0, 0) на окружности?
Ответ: 1) (х + 1)2 + (у – 2)2 = 4, если раскроем скобки, то уравнение примет вид:
х2 + у2 + 2х – 4у + 1 = 0
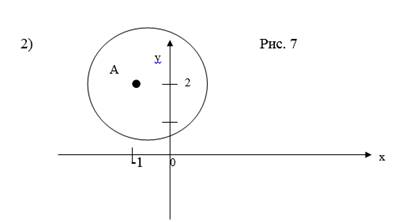
5) О (0,0) не лежит на окружности, т. к. координаты этой точки не удовлетворяют уравнению: 0+0+0 + 0+1 ≠ 0.
Практическое занятие 5
Тема: «Действия с комплексными числами, записанными в различных формах. Решение уравнений»
Цель
- изучить понятие о комплексных числах и действий с ними;
- научится выполнять действия с комплексными числами и решать уравнения с комплексными числами
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию.
Основная задача – изучение множества комплексных чисел, формирование навыков выполнения алгебраических действий над комплексными числами
Указания: выполнять работу по алгоритму
Вопросы практической работы: множество комплексных числе, мнимая единица, арифметические действия с комплексными числами. Решение квадратных уравнений с дискриминантом <0. Область применения комплексных чисел в профессиональной деятельности.
Определение. Комплексным числом z называют сумму действительного числа и чисто мнимого числа.
z = a+ib, где аϵ R, bϵ R, i – мнимая единица
Это алгебраическая форма комплексного числа z.
Определение. Два комплексных числа z1 = a1 +ib1 и z2 = a2 +ib2 называются равными, если соответственно равны их действительные и мнимые части:
a1 = a2; b1 =b2;
Минимальные условия, которым должны удовлетворять
комплексные числа:
(записываем в тетрадь)
1. Существует комплексное число, квадрат которого равен -1. Такой элемент называют мнимой единицей и обозначают i. (Обозначение предложил Эйлер в 18 веке)
i2 = -1
2. Множество комплексных чисел содержит все действительные числа.
3. Операции сложения, вычитания, умножения и деления комплексных чисел удовлетворяют обычным законам арифметических действий.
4. Арифметические операции для комплексных чисел.
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.
.
|
Арифметическое действие с комплексными числами |
z1 = a1 + b1i z2 = a2 + b2i |
|
Сложение |
z = (a1 + a2) + (b1 + b2) i |
|
Вычитание |
z = (a1 - a2) + (b1 - b2) i |
|
Умножение |
z = (a1a2 – b1b2) + (a1b2 + a2b1) i |
1) Сложение.
Суммой комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть - сумме мнимых частей чисел z1 и z2 , то есть z = (a1 + a2) + (b1 + b2) i.
2) Вычитание.
Вычесть из комплексного числа z1 комплексное
число z2, значит найти такое комплексное
число z, что z + z2 = z1.
z = (a1 - a2) + (b1 - b2) i.
3) Умножение.
Произведением комплексных чисел z1=a1+ b1 i и z2=a2+b2 i называется комплексное число z, определяемое равенством:
z = (a1a2 – b1b2) + (a1b2 + a2b1) i.
.
Даны
комплексные числа z1 = 1 - 2i, z2 = 3 + i, z3 =
-7i
Найти:
а) z1 + z2; б) z1 – z2; в) z1z2.
Решение.
а) z1 + z2 = (1 - 2i) + (3 + i) =1 - 2i +3 + i = (1 + 3) + (-2i + i) =4 - i;
б) z1 – z2 = (1 - 2i) - (3 + i) = 1 - 2i - 3 - i = (1 - 3) + (-2i - i) = – 2 - 3i;
в) z1z2 = (1 -
2i)∙ (3 + i) = 1∙3 - 2i∙3 + 1∙i - 2i∙i= 3 -
6i + i + 2 = 5 - 5i
(здесь учтено, что i2 =
– 1).
5. Решение заданий на выполнение действий с комплексными числами
1-8. Произведите сложение и вычитание комплексных чисел:
1)
(3 + 5i) + (7 – 2i).
2) (6 + 2i) + (5 + 3i).
3) (– 2 + 3i) + (7 – 2i).
4) (5 – 4i) + (6 + 2i).
5) (3 – 2i) + (5 + i).
6) (4 + 2i) + (– 3 + 2i).
7) (– 5 + 2i) + (5 + 2i).
8) (– 3 – 5i) + (7 – 2i).
9-14. Выполните умножение комплексных чисел:
9) (2 + 3i)(5
– 7i).
10) (6 + 4i)(5 + 2i).
11) (3 – 2i)(7 – i).
12) (– 2 + 3i)(3 + 5i).
13) (1 –i)(1 + i).
14) (3 + 2i)(1 + i).
4) Деление.
|
Арифметическое действие с комплексными числами |
z1 = a1 + b1i z2 = a2 + b2i |
число z1 = a1 - b1i сопряженное ему число z2 = a2 - b2i |
|
Сложение |
z = (a1 + a2) + (b1 + b2) i |
|
|
Вычитание |
z = (a1 - a2) + (b1 - b2) i |
|
|
Умножение |
z = (a1a2 – b1b2) + (a1b2 + a2b1)i |
|
|
Деление |
|
|
Определение. Числа z = a+ib и z = a - ib называются комплексно– сопряженными.
Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
Произведение двух сопряженных чисел всегда равно действительному числу. Воспользуемся этим свойством для выполнения деления двух комплексных чисел. Чтобы выполнить деление, произведем дополнительное действие: умножим делимое и делитель на комплексное число, сопряженное делителю.
Пример 1:
![]()
Решение.
Произведем умножение для делимого и делителя в отдельности:
(2 + 3i)(5 + 7i) = 10 + 14i + 15i + 21i2 = – 11 + 29i;
(5 – 7i)(5 + 7i) = 25 – 49i2 = 25 + 49 = 74.
Итак,
![]() =
= ![]() +
+![]() i
i
Примеры для самостоятельной работы.
15-20. Произведите деление комплексных чисел:
15)
(2 + 3i):(5 – 7i).
16) (6 + 4i):(5 + 2i).
17) (3 – 2i):(7 – i).
18) (– 2 + 3i):(3 + 5i).
19) (1 –i):(1 + i).
20) (3 + 2i):(1 + i).
Решение уравнений

Т.о., если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня.
Практическое занятие 6
Тема: «Раскрытие неопределенностей»
Цель
- изучить понятие предела, правил его вычисления;
- рассмотреть виды неопределенностей
- научится раскрывать неопределенности вида 0/0, ∞/∞
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию.
Основная задача – изучение понятия предела, формирование навыков вычисления пределов и раскрытия неопределенностей вида 0/0, ∞/∞
Указания: выполнять работу по алгоритму
Вопросы практической работы: предел функции в точке, правила его вычисления. Область применения пределов в экономике и профессиональной деятельности.
Основные свойства пределов
1. Функция не может иметь более одного предела (при одной и той же базе).
2.
Предел постоянной равен самой этой постоянной: ![]() , с – постоянная.
, с – постоянная.
3.
Предел суммы функций равен сумме пределов этих функций: ![]()
4.
Предел произведения функций равен произведению пределов этих функций: ![]()
Отсюда
следует, что постоянный множитель можно выносить за знак предела: ![]()
5.
Предел частного двух функций равен частному пределов этих функций (если предел
делителя не равен нулю): ![]()
6.
(свойство предела сложной функции) Если ![]() , то предел сложной функции
, то предел сложной функции![]() .
.
7.
Если при базе В (т.е. в некоторой окрестности точки х0или при достаточно
больших х) f1(х) < f2(х), то![]() .
.
Отметим, что в перечисленных свойствах предполагается существование пределов функций f1(х) и f2(х), из чего следуют заключения о значениях пределов суммы, произведения или частного этих функций. Но при этом из существования предела суммы, произведения или частного функций не обязательно следует, что существуют пределы самих слагаемых, сомножителей или делимого и делителя.
Например, ![]() , но при этом
, но при этом![]() не существует.
не существует.
Замечательные пределы
Для вычисления пределов функций в некоторых случаях удобно использовать так называемые замечательные пределы(здесь рассматриваются без доказательства).
Первый замечательный предел
![]()
Второй замечательный предел
Для числовой последовательности (1 + 1/n)n:
![]()
Непрерывность функции
Функция f(x) называется непрерывной в точкеx0, если она удовлетворяет трем условиям:
1) определена в точке (т.е. существует f(x0));
2) имеет конечный предел при х®х0;
3) этот предел равен значению функции в точке х0,
т.е. ![]() .
.
Поясним определение непрерывности следующим примером (рисунок). На рисунке представлены графики четырех функций y=f(x), первые три из которых не являются непрерывными в точкеx= 0, а четвертая – является.
В самом деле, функция (а) не является непрерывной в точке x= 0, так как вообще не определена в этой точке (т.е. нарушено первое условие непрерывности).
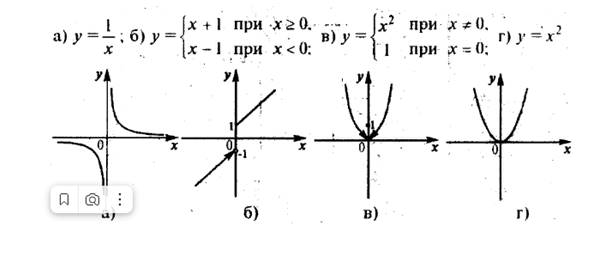
Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел
следующим образом ![]() .
.
Вычислим предел: ![]()
Подставляем вместо х –
3. ![]()
Заметим, что предел числа равен самому числу.
Примеры: вычислите пределы 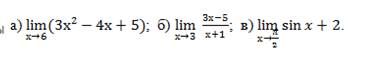
Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).
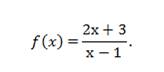
Вычислим значение функции в точке x0 = 3 и значение его предела в этой точке.
Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x0 = 3.
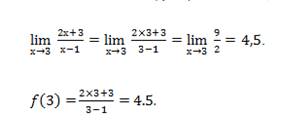
Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.
Основные виды неопределенностей: 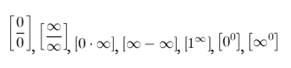
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
- упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
- если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.

![]()


Практическое занятие 7
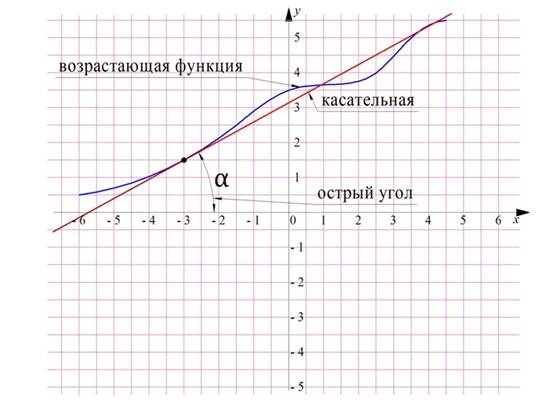
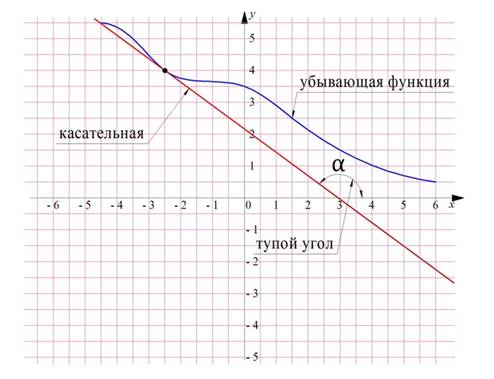
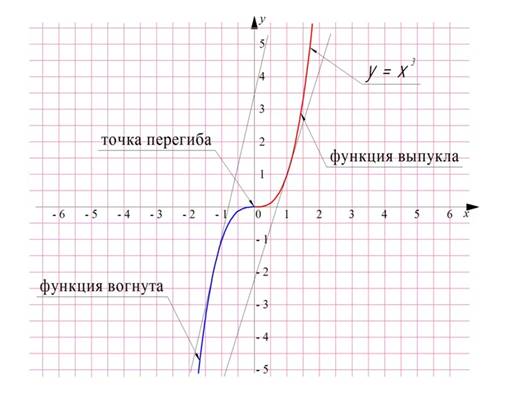
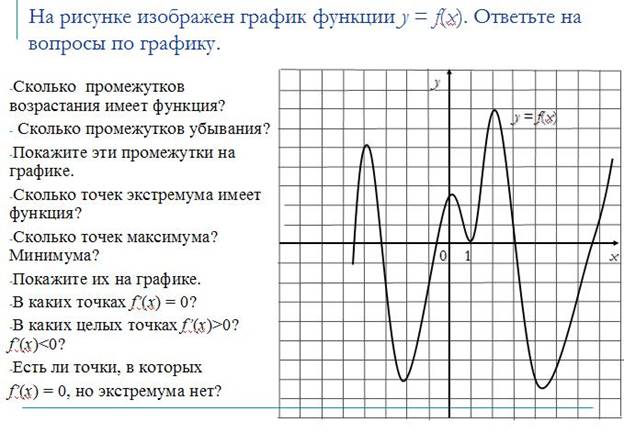
Тема: «Вычисление производных, исследование функции»
Цель
- повторить понятие производной, таблицу производных;
- закрепить умения вычисления производных
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию.
Основная задача – закрепление знаний о производных и умения их вычислять
Указания: выполнять работу по алгоритму
Вопросы практической работы: таблица производных и алгоритм вычисления производной. Область применения производных в экономике и профессиональной деятельности.

- Рассмотрим функцию f(x) =
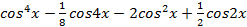
D(f) = R
- f’(x) =
= ![]()
![]()
f’(x) =0 при любом х, значит функция y = f(x) – постоянна на R.
- Найдем значение функции в любой точке, например х = 0
f(0) = ![]()
Вывод: равенство![]() выполняется
при любом х
выполняется
при любом х
Решите
уравнение ![]()
|
Анализ условия задачи и поиск решения |
|
|
|
|
|
Какого вида уравнение? |
Иррациональное |
|
С чего начинается решение иррационального уравнения? |
С нахождения области допустимых значений: 2х – 1 ≥ 0 х ≥ 0,5 ОДЗ = [0,5; +∞) |
|
Какие способы решения иррациональных уравнений существуют? |
1)возвести обе части в 4-ую степень; 2) заменой переменной; 3) графический. |
|
|
|
|
1) Начните решение первым способом |
При возведении обеих частей уравнения в 4-ую степень появится х8, х7,…, х2, х, а это уравнение 8-ой степени. |
|
Сможем ли мы решить уравнение первым способом? |
Нет |
|
2) второй способ |
Нужно произвести замену Выразим х: x = (t4 + 1)/2 Подставляя полученные выражения в исходное уравнение, получим уравнение 8-ой степени. |
|
Можно ли решить уравнение вторым способом? |
Нет |
|
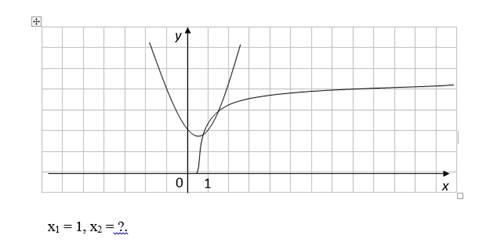
3) Решим уравнение третьим способом (графически) |
|
Решение:
1) Построим
графики функций у = ![]() и
у =
и
у = ![]()
2) Найдем точки пересечения графиков функций.
Графиком первой функции является парабола с вершиной в точке (x0, y0)
х0 = ![]() ;
y0 = y(x0) = 1,75
;
y0 = y(x0) = 1,75
|
х |
1 |
2 |
|
у |
2 |
4 |
Дополнительные точки:
|
х |
0,5 |
1 |
8,5 |
|
у |
0 |
2 |
4 |
График второй функции – ветвь параболы, направленная вдоль оси Ох.
- Рассмотрим
функцию
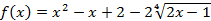 ,
D(f) = [0,5; +∞)
,
D(f) = [0,5; +∞) 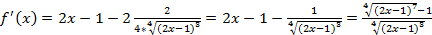
 f’(x)=0 при х = 1
f’(x)=0 при х = 1
x = 1 – точка минимума
fmin= f(1) = 2 – 2 = 0
- Так как функция убывает на отрезке [0,5; 1], то во всех точках промежутка [0,5; 1) значения функции > 0;
так как функция возрастает на промежутке [1; +∞], то во всех точках промежутка (1; +∞) значения функции > 0;
Значит, уравнение имеет единственный корень х = 1
Ответ: х = 1.
План исследования.
1. Найти область определения.
2. Исследовать на чётность и нечётность, периодичность (для тригонометрических) функцию.
3. Найти точки пересечения графика с осями координат (с осью Ох и осью Оу)
4. Найти критические точки.
5. Найти промежутки монотонности (возрастания и убывания).
6. Найти точки экстремума и экстремум функции (хmax, xmin, ymax, ymin)
7. Занести все полученные данные в таблицу
8. Построить график.
9. Если необходимо вычислить дополнительные точки.
п 2 Функция ни четная, ни нечетная, непериодическая.
п3 Точки пересечения
с осью х: (0; 0) и (-3; 0), т. к.
f(x) = 0, т. е. ⅓x³ + 2x² + 3x = 0
⅓x (x² + 6 x + 9) = 0
⅓x (х + 3)² = 0
х = 0; х = -3
с осью у: (0; 0).
Что еще можно сделать, чтобы более точно построить график? (Можно найти несколько дополнительных точек, принадлежащих графику функции).
График функции f(x) =⅓x³ + 2x² + 3x
Практическое занятие 8
Тема: «Вычисление приближенных значений функции. Оценка погрешности»
Цель
- повторить понятие погрешностей и виды погрешностей;
- закрепить умения вычисления погрешностей
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию.
Основная задача – закрепление знаний о погрешностях и умения их вычислять
Указания: выполнять работу по алгоритму
Вопросы практической работы: виды погрешностей. Область применения погрешностей в экономике и профессиональной деятельности.
По графику функции у=х 2 найдем приближенное значение функции при заданных значениях аргумента (примерно по графику 2, 3 и 4,4), затем по формуле у=х 2 при х =1, 5 и х = 2,1 точные значения функции при тех же значениях аргумента.
Затем находим на сколько приближенное значение отличается от точного значения.
Вводится определение абсолютной и относительной погрешности.
Абсолютная погрешность показывает на сколько приближенное значение отличается от точного, т.е. точность приближения.
Относительная погрешность оценивает качество измерения и выражается в процентах.
Если х ≈ α, где х – точное значение, а α – приближенное, то абсолютная погрешность будет: │х – α │, а относительная: (│х – α │∕ │α│)х 100%
В том случае, когда невозможно найти абсолютную погрешность, необходимо указать такое число, больше которого абсолютная погрешность быть не может.
Пример округления десятичных дробей.
1. Рассмотрим вычисление абсолютной и относительной погрешности
Дана функция у=х³, найти абсолютную и относительную погрешность
при х=0,2 , при х=1,6 , при х=1,9
По графику.
При х=0,2 у≈0,05
При х=1,6 у≈3,8
При х=1,9 у≈6,6
По формуле.
При х=0,2 у=0,2³=0,008
При х=1,6 у=1,6³=4,096
При х=1,9 у=1,9³=6,859
Абсолютная погрешность.
\0,008-0,05\=\-0,042\=0,042
\4,096-3,8\=\0,296\=0,296
\6,859-6,6\=\0,259\=0,259
Найдем теперь относительную погрешность.
17,26≈17,3 \17,26-17,3\=\-0,04\=0,04
12,034≈12,0 \12,034-12,0\=\0,034\=0,034
8,654≈8,7 \8,654-8,7\=\-0,046\=0,046
Отчего зависит точность приближенного значения?
Она зависит от многих причин. Если приближенное значение получено при измерении, то его точность зависит от прибора, с помощью которого выполнялось измерение. Никакое измерение не может быть выполнено совершенно точно. Даже сами меры заключают в себе погрешность. Изготовить совершенно точные метровые линейки, килограммовую гирю, литровую кружку чрезвычайно трудно и закон допускает при изготовлении некоторую погрешность.
Например, при изготовлении метровой линейки допускается погрешность 1мм. Само измерение тоже вводит неточность, погрешность в гирях, весах. Например на линейке, которой мы пользуемся, нанесены деления через 1мм, т.е. 0,1см, значит точность измерения этой линейкой до 0,1 ( ≤ 0,1). На медицинском термометре деления через 0,10 , значит точность до 0,1 ( ≤ 0,1). На весах деления нанесены через 200г, значит точность до 200 ( ≤ 200).
Округляя десятичную дробь до десятых точность будет до 0,1 ( ≤ 0,1); до сотых – точность до 0,01 ( ≤ 0,01).
Точнейшие в мире измерения производятся в лабораториях Института мер.
Всегда ли можно найти абсолютную и относительную погрешности?
Не всегда можно найти абсолютную погрешность, так как неизвестно
точное значение величины, а отсюда и относительную погрешность.
В этом случае принято считать что абсолютная погрешность не превосходит цены деления шкалы прибора. Т.е. если например цена деления линейки 1мм = 0,1см, то абсолютная погрешность будет с точностью до 0,1 ( ≤ 0,1) и будет определена только оценка относительной погрешности (т.е. ≤ какому числу %).
Часто приходится с этим встречаться в физике при демонстрации опытов, при выполнении лабораторных работ.
Задача. Найдем относительную погрешность при измерении длины листа тетради линейками: одна – с точностью до 0,1см (деления через 0,1см); вторая - с точностью до 1см (деления через 1см).
ℓ1 = 20,4см ℓ2 = 20,2см
0,! : 20,4 = 0,0049 = 0,49% 1 : 20,2 = 0,0495 = 4,95%
Говорят, относительная погрешность в первом случае до 0,49%(т.е ≤ 0,49%), во втором случае до 4,95% (т.е. ≤ 4,95%).
В первом случае точность измерения выше. Мы говорим не о величине
относительной погрешности, а ее оценке.
На производстве при изготовлении деталей мы пользуемся
штангенциркулем (для измерения глубины; диаметра: наружного и внутреннего).
Абсолютная погрешность при измерении этим прибором составляет точность до 0,1мм. Найдем оценку относительной погрешности при измерении штангенциркулем:
d = 9,86см = 98,6мм
0,1 : │98,6│= 0,1 : 98,6 = 0,001 = 0,1%
Относительная погрешность с точностью до 0,1% (т.е. ≤ 0,1%).
Если сравнить с предыдущими двумя измерениями, то получается точность измерения выше.
Из практических примеров можно сделать вывод: что точных значений быть не может, производя измерения в обычных условиях.
Но чтобы точнее выполнить измерение нужно взять измерительный прибор цена деления которого как можно меньше.
2.Выполнение упражнений на закрепление с компьютерных слайдов.
Ответим на вопрос: При измерении длины стержня пользовались линейкой, штангенциркулем, микрометром. При этом были получены результаты 17,9 мм; 18 мм; 17,88 мм. Каким прибором измеряли?
Найдите абсолютную погрешность, полученную в результате округления
а) до десятых 6,56; 0,475; 3,671
б) до десятков 124; 361; 720
Подведение итогов урока.
Сформулируйте определение абсолютной погрешности.
Если нельзя найти абсолютную погрешность, каким понятием пользуются? (точность измерения).
Чему равна точность измерения? (цене деления прибора).
Приведите примеры точности измерения некоторых приборов.
Для чего используется относительная погрешность? Приведите пример.
Что такое относительная погрешность?
Домашнее задание:
При вычислении дробь 11/20 заменили десятичной дробью 0,5. Какова абсолютная погрешность этого приближения?
Найдите с помощью графика функции y=x2 значение y при x =2,4.Вычислите абсолютную погрешность полученного приближенного значения.
Тренировочные упражнения (в случае наличия времени)
|
Вариант 1 |
Вариант 2 |
|
1. Построить график функции у = х3 |
1. Построить график функции у = х2 |
|
Пользуясь графиком закончить запись: если х = 1,5, то у ≈ если х = -0,5, то у ≈ б) у = 4 при х ≈ |
Пользуясь графиком закончить запись: если х = 2,5, то у ≈ если х = -1,5, то у ≈ б) у = 5 при х ≈ |
|
2. Округлить число 0,356 до десятых и найти: a) абсолютную погрешность приближения; б) относительную погрешность приближения |
2. Округлить число 0,188 до десятых и найти: a) абсолютную погрешность приближения; б) относительную погрешность приближения |
Практическое занятие 9
Тема: «Приложения определенного интеграла»
Цель
- повторить понятие определенного интеграла;
- закрепить умения вычисления определенного интеграла
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию.
Основная задача – закрепление знаний об интегралах и умения их вычислять
Указания: выполнять работу по алгоритму
Вопросы практической работы: определенный интеграл. Таблица интегралов. Область применения интегралов в экономике и профессиональной деятельности.
Применение определенного интеграла не ограничивается вычислением площади фигуры.
Определенный интеграл помогает решать ряд физических и общетехнических задач, поэтому знания, полученные вами на этом уроке, помогут в вашей дальнейшей учебе и практической деятельности.
1. Задача о вычислении пути
Согласно
физическому смыслу первой производной, производная функции в точке есть
мгновенная скорость точки, т.е. ![]() .
Отсюда,
.
Отсюда, ![]() . Интегрируя полученное
равенство в пределах от t1 до t2 получаем
. Интегрируя полученное
равенство в пределах от t1 до t2 получаем
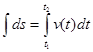
Тогда путь,
пройденный точкой при неравномерном движении по прямой с переменной скоростью u(е) за отрезок времени [![]() ]выражается интегралом
]выражается интегралом
S=![]() u(t)dt.
(1)
u(t)dt.
(1)
Пример 1.
Скорость прямолинейного движения тела выражается формулой u = 2t+3t![]() (м/с). Найти путь,
пройденный телом за 5 секунд от начала движения.
(м/с). Найти путь,
пройденный телом за 5 секунд от начала движения.
Решение.
S=![]() 2t+3t
2t+3t![]() )dt
= (t
)dt
= (t![]() )
)![]() =150(м).
=150(м).
Пример 2.
Два тела начали двигаться одновременно из одной точки в одном направлении по
прямой. Первое тело движется со скоростью v![]() =(6t
=(6t![]() +2t)м/с,
второе – со скоростью v
+2t)м/с,
второе – со скоростью v![]() =(4t+5) м/с. На каком расстоянии друг от друга они окажутся
через 5с?
=(4t+5) м/с. На каком расстоянии друг от друга они окажутся
через 5с?
Решение. Искомая величина есть разность расстояний, пройденных телами за 5 с.
S![]() =
=![]() 6 t
6 t![]() +2t)dt
= (2t
+2t)dt
= (2t![]() )
)![]() =275(м)
=275(м)
S![]() =
=![]() 4 t+5)dt = (2t
4 t+5)dt = (2t![]() )
)![]() =75(м)
=75(м)
Таким образом,
S=S![]() -S
-S![]() = 275-75=200 (м).
= 275-75=200 (м).
2. Задача о вычислении работы переменной силы
Пусть материальная точка под действием силы F движется по прямой. Если действующая сила постоянна, а пройденный путь равен s, то как известно из курса физики, работа А этой F вычисляется по формуле:
А= F*s
Работу переменной силы f(x) при перемещении по оси Оx материальной точки от x=a до x=b, находим по формуле (3):
A=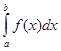 (3)
(3)
Решение задач на вычисление работы силы упругости, связанных с растяжением и сжатием пружин, основывается на законе Гука. По закону Гука сила F, растягивающая или сжимающая пружину, пропорциональная этому растяжению или сжатию, т.е. F=kx, где x – величина растяжения или сжатия, k – коэффициент пропорциональности.
Пример 1. Сила
упругости F пружины, растянутой на 1![]() = 0,05м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на1
= 0,05м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на1![]() =0,1м?
=0,1м?
Решение. Подставив данные в формулу закона Гука, получим: 3=k*0.05, т.е k=60, следовательно, сила упругости выражается соотношением F=60x. Найдем работу переменной силы по формуле (3), полагая, что а=0; b=0,1:
A=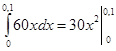 =0,3Дж
=0,3Дж
3. Задача о силе давления жидкости
Согласно закону Паскаля величина P давления жидкости на горизонтальную площадку вычисляется по формуле P=gphS, (4)
Где g –
ускорение свободного падения в м/с![]() ;
;
p– плотность жидкости в кг/м![]() ;
;
h – глубина погружения площадки в м;
S –
площадь площадки в м![]() .
.
По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.
Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, у1 = f1(x) и у2=ƒ2(х); система координат выбрана так, как указано на рисунке 1.
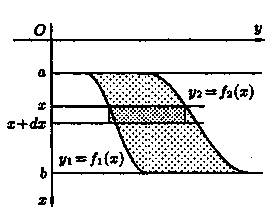
рисунок 1
Для решения
задачи разобьем пластину на n частей ( малых горизонт
альных полосок) прямыми, параллельными поверхности жидкости (т.е. параллельными
оси OY). На глубине х выделим одну из них и обозначим
через f(x) ее длину, а через ![]() ее ширину. Приняв полоску за
прямоугольник, находим ее площадь
ее ширину. Приняв полоску за
прямоугольник, находим ее площадь ![]() .
.
![]()
Найдем дифференциал dp этой функции.
![]()
![]()
Тогда по закону Паскаля
Интегрируя полученное равенство в пределах от х = а до х = b, получим
P=g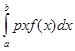 (5)
(5)
Пример
Аквариум имеет
форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды
1000 кг/м![]() ), наполняющей аквариум,
на одну из его вертикальных стенок, размеры которой 0,4мx0,7м.
), наполняющей аквариум,
на одну из его вертикальных стенок, размеры которой 0,4мx0,7м.
Решение. Выберем систему координат так, чтобы оси Оy и Оx соответственно содержали верхнее основание и боковую сторону вертикальной стенки аквариума. Для нахождения силы давления воды на стенку воспользуемся формулой (5). Стенка имеет форму прямоугольника, поэтому f(x)=0,7х, xÎ[0;0,4]. Так как пределы интегрирования а=0 и b=0,4, то получим:
P=g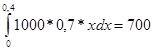
![]() =56g»549H
=56g»549H
Практическое занятие 10
Тема: «Вычисление вероятностей случайных событий»
Цель
- изучить понятия вероятности случайного, достоверного, невозможного событий;
- сформировать умения определения вероятности случайного, достоверного, невозможного событий;
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию.
Основная задача – изучение понятия случайное событие; формирование элементарных умений вычислять вероятность случайного события
Указания: выполнять работу по алгоритму
Вопросы практической работы: события, испытания, вероятность, случайное событие, невозможного и достоверного события; понятие классической вероятности события; поиск вероятности случайного события, пользуясь определением классической вероятности; поиск вероятности суммы событий.
.
Событие, которое может произойти, а может не произойти в процессе наблюдения или эксперимента, называют случайным событием. Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей.
Прозвенел звонок, выпал снег, черный кот перебежал дорогу – все это события. Каждое из них при одних условиях могло произойти, при других – нет. Поэтому, эти события называют случайными.
Два события, которые в данных условиях могут происходить одновременно, называются совместными, а те, которые не могут происходить одновременно, - несовместными.
Примеры.
1. Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» - несовместные.
2. Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместные.
Равновозможными называются события, когда в их наступлении нет преимуществ
Неравновозможные события те, у которых в наступлении одного из событий есть какое-то преимущество.
Примеры.
1. Появление герба или надписи при бросании монеты представляют собой равновероятные события.
2. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
Событие, которое происходит всегда, называют достоверным событием.
Вероятность достоверного события равна 1.
Событие, которое не может произойти, называется невозможным.
Вероятность невозможного события равна 0.
Примеры.
1. В следующем году снег не выпадет. При бросании кубика выпадет семерка. Это невозможные события.
2. В следующем году снег выпадет. При бросании кубика выпадет число, меньше семи. Ежедневный восход солнца. Это достоверные события.
3. Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара – достоверное событие; появление белого шара – невозможное событие.
Теория вероятностей – раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. (Советский энциклопедический словарь, 1982 год)
Теория вероятностей – это математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким – либо образом с первыми. (А.А.Боровков «Теория вероятностей», М.: Наука, 1986 год.)
Вероятность – это численная характеристика реальности появления того или иного события.
Классическое определение вероятности.
Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие А, к общему числу всех (равновозможных между собой) исходов этого испытания.
Для решения задач используют алгоритм нахождения вероятности случайного события.
Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти:
число N всех возможных исходов данного испытания;
количество N(A) тех исходов, в которых наступает событие А;
частное ![]() оно и будет равно вероятности события А.
оно и будет равно вероятности события А.
Принято
вероятность события А обозначать так: Р(А). Значит Р(А) = ![]()
Пример 1. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность Р(А) того, что взятый наудачу подшипник окажется стандартным.
Решение. Число стандартных подшипников равно 1000 – 30 = 970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из N = 1000 равновероятных исходов, из которых событию А благоприятствуют N(A) = 970 исходов.
Поэтому ![]() Р(А)
=
Р(А)
= ![]() Ответ:
0,97.
Ответ:
0,97.
Пример 2. Найдем вероятность того, что при одном бросании игральной кости (кубика) выпадает: а) три очка; б) число очков, кратное трем; в) число очков больше трех; г) число очков, не кратное трем.
Решение. Всего имеется N=6 возможных исходов: выпадение 1,2,3,4,5,6 очков. Считаем, что эти исходы равновозможны.
а) Только при одном из исходов N(А)=1 происходит интересующее нас
событие А – выпадение трех очков. Вероятность
этого события ![]() .
.
б) При двух исходах N(B) = 2 происходит
событие B: выпадение числа очков кратных трем: выпадение или трех или
шести очков. Вероятность такого события ![]() .
.
в) При трех исходах N(C) = 3 происходит
событие C: выпадение числа очков больше трех: выпадение четырех, пяти или
шести очков. Вероятность этого события ![]() .
.
г) Из шести возможных выпавших чисел четыре (1, 2, 4 и 5) не кратны трем, а остальные два (3 и 6) делятся на три. Значит, интересующее нас событие D,
наступает в четырех случаях, т.е. N(D) =
4. Вероятность такого события: ![]() .
.
Ответ: а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ;
г)
;
г) ![]() .
.
Для вычисления вероятности часто используют правило умножения.
Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Пример 3.
Найдем вероятность того, что при подбрасывании двух костей суммарное число очков окажется равным 5.
Решение. Возможно следующее сочетание очков на первой и второй костях:
1 + 4, 2 + 3, 3 + 2, 4 + 1 – четыре
благоприятных случая (N(A) = 4). Всего возможных исходов N = 6·6 = 36
(по шесть для каждой кости). Тогда вероятность рассматриваемого события ![]() Ответ:
Ответ: ![]() .
.
Вероятность Р(А) некоторого события ![]() .
.
При решении некоторых задач удобно использовать свойство вероятностей противоположных событий.
События А и В называются противоположными, если всякое наступление события А означает ненаступление события В, а ненаступление события А – наступление события В.
Событие, противоположное событию А,
обозначают символом ![]() . Сумма
вероятностей противоположных событий равна 1.
. Сумма
вероятностей противоположных событий равна 1. ![]() .
.
Пример 4.
1.
Бросаем один раз игральную кость. Событие А – выпадение четного числа очков,
тогда событие ![]() -
выпадение нечетного числа очков.
-
выпадение нечетного числа очков.
2. В среднем из 1000 аккумуляторов, поступивших в продажу, 6 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.
Решение. Элементарный исход – случайно выбранный аккумулятор. Поэтому
N = 1000.
Событию А = {аккумулятор исправен} благоприятствуют 1000 – 6 = 994 исхода.
Поэтому N(A) = 994.
Тогда ![]()
Ответ: 0,994.
Эту задачу можно решить с помощью формулы
вероятности противоположного события ![]() =
{аккумулятор неисправен}. Тогда N(Ā)=6.
=
{аккумулятор неисправен}. Тогда N(Ā)=6.
Имеем ![]() =
= ![]() Значит, P(A)
= 1-
Значит, P(A)
= 1- ![]() =1 –
0,006 = 0,994.
=1 –
0,006 = 0,994.
Ответ: 0,994.
Задачи:
1. Вася, Петя, Коля и Леша бросили жребий - кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
2. Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, больше чем 4?
3. В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 8 очков.
4. В случайном эксперименте монету бросили три раза. Какова вероятность того, что орел выпал ровно два раза?
5. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5- из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
6. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
7. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решения к задачам
1. Случайный эксперимент – бросание жребия. Элементарное событие в этом эксперименте – участник, который выиграл жребий. Перечислим их: (Вася), (Петя), (Коля) и (Лёша).
Общее число элементарных событий N = 4. Жребий подразумевает, что элементарные события равновозможны. Событию A = {жребий выиграл Петя}благоприятствует только одно элементарное событие (Петя). Поэтому N(A)=1.
Ответ: 0,25.
2. Случайный эксперимент – бросание кубика. Элементарное
событие –число на выпавшей грани. Граней всего шесть. Перечислим все
элементарные события: 1,2,3,4,5 и 6. Значит, N=6. Событию A={выпало
больше, чем 4} благоприятствует два элементарных события: 5 и 6.
Поэтому N(A) = 2. Элементарные события равновозможны, поскольку
подразумевается, что кубик честный. Поэтому ![]() Ответ:
Ответ: ![]() .
.
3. Элементарный исход в этом опыте – порядочная пара чисел. Первое число выпадает на первом кубике, а второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют результату первого броска, столбцы – результату второго броска. Всего элементарных событий N = 3.
1 2 3 4 5 6
2
|
3 |
4 |
5 |
6 |
7 |
|
|
3 |
4 |
5 |
6 |
7 |
8 |
|
4 |
5 |
6 |
7 |
8 |
9 |
|
5 |
6 |
7 |
8 |
9 |
10 |
|
6 |
7 |
8 |
9 |
10 |
11 |
|
7 |
8 |
9 |
10 |
11 |
12 |
1
2
3
4
5
6
Напишем в каждой клетке таблицы сумму выпавших очков и закрасим клетки где
сумма равна 8. Таких ячеек 5. Значит событию А = {сумма равна 8}
благоприятствует пять элементарных исходов. Следовательно, N(A) = 5.
Поэтому ![]() Ответ:
Ответ: ![]()
Орёл обозначим буквой О, решку – буквой Р. В описанном эксперименте элементарные исходы – тройки, составленные из букв О и Р. Выпишем все их в таблицу:
Элементарный исход
|
Число орлов |
|
|
ООО |
3 |
|
ООР |
2 |
|
ОРО |
2 |
|
ОРР |
1 |
|
РОО |
2 |
|
РОР |
1 |
|
РРО |
1 |
|
РРР |
0 |
Всего исходов получилось 8. Значит, N=8.
Событию А = {орёл выпал ровно два раза} благоприятствует элементарные события
ООР, ОРО, РОО. Поэтому N(A)=3. Тогда ![]() Ответ: 0,375.
Ответ: 0,375.
5. Элементарный исход –
спортсмен, который выступает последним. Последним может оказаться любой
спортсмен. Всего спортсменов N=4+7+9+5+5=25. Событию А = {последний из Швеции}
благоприятствуют только 9 исходов (столько, сколько участвует шведских
спортсменов). Поэтому N(A)=9. Тогда ![]() Ответ:
0,36.
Ответ:
0,36.
6. Элементарные события – спортсменка,
выступающая первой. Поэтому N=20. Чтобы найти число элементарных событий,
благоприятствующих событию А = {первой выступает спортсменка из Китая}, нужно
подсчитать число спортсменок из Китая: N(A)=20-(8+7)=5. Все элементарные
события равновозможны по условию задачи, поэтому ![]()
Ответ: 0,25.
7. Элементарный исход – случайно выбранная сумка. Поэтому N = 108.
Событию А = {качественная сумка} благоприятствуют 100 исходов.
Поэтому N(A) = 100.
Практическое занятие 11
Тема: «Анализ, обработка и графическое представление данных»
Цель
- повторить основные понятия математической статистики;
- закрепить умения графического представления данных
- развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию.
Основная задача – освоить и отработать технологию построения и редактирования различных видов диаграмм и графиков с помощью компьютерных технологий (программа Excel)
Указания: выполнять работу по алгоритму
Вопросы практической работы: элементы математической статистики, виды графиков. Возможности программы Excel при построении графиков.
Диаграмма – объект ЭТ, наглядно показывающий соотношение каких-либо величин.
Это средство наглядного графического изображения информации, предназначенное для сравнения нескольких величин или нескольких значений одной величины.
Диаграмма связана с данными, на основе которых она создана, и автоматически обновляется при их изменении.
Диаграммы могут быть различных типов и соответственно представлять данные в различной форме. Для каждого набора данных важно правильно подобрать тип создаваемой диаграммы.
Для наглядного сравнения величин используются линейчатые диаграммы, в которых высота столбца пропорциональна значению величины. Линейчатые диаграммы могут быть плоскими или объемными, причем столбцы могут быть расположены как вертикально (гистограмма), так и горизонтально. Например, с помощью гистограммы можно наглядно представить данные о численности населения различных стран мира.
Для отображения величин частей некоторого целого применяется круговая диаграмма, в которой величина кругового сектора пропорциональна значению части. Круговы диаграммы могут быть плоскими или объемными, причем секторы могут быть раздвинуты. Пример (доли цен отдельных устройств компьютера в его общей цене.
Для построения графиков функций и отображения изменения величин в зависимости от времени используются диаграммы типа график.
При создании диаграмм, прежде всего, необходимо выделить диапазон ячеек, содержащих исходные данные для ее построения.
Выделенный диапазон включает в себя как ряды данных, так и категории.
Ряды данных – это множество значений, которые необходимо отобразить на диаграмме (численность населения, цена отдельного устройства).
Категории задают положение значения ряда данных на диаграмме. Подписи под столбцами, названия секторов ( Название страны, название устройства)
Ряды данных и категорий могут размещаться как в столбцах, так и в строках электронной таблицы.
![]() Построение диаграммы
начинается с выбора диапазона тех данных, которые следует отразить. Затем на
вкладке Вставка в группе Диаграммы выбирается
кнопка типа создаваемой диаграммы (Гистограмма, Круговая, Линейчатая и т. д.), которая
представляет собой выпадающее меню с вариантами диаграмм.
Построение диаграммы
начинается с выбора диапазона тех данных, которые следует отразить. Затем на
вкладке Вставка в группе Диаграммы выбирается
кнопка типа создаваемой диаграммы (Гистограмма, Круговая, Линейчатая и т. д.), которая
представляет собой выпадающее меню с вариантами диаграмм.
Созданная диаграмма отобразится в рабочем листе, после чего станет доступна контекстная вкладка Работа с диаграммами с тремя наборами инструментов (вкладками) для изменения диаграмм:
В процессе редактирования можно изменить цвет и стиль линий, размеры диаграммы, цену делений шкалы, вид фигуры ряда, переместить текст и т. п.
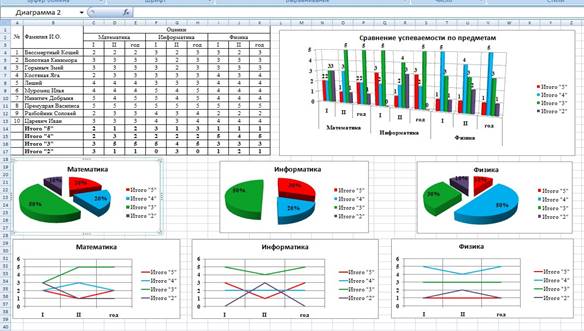
Задание 1
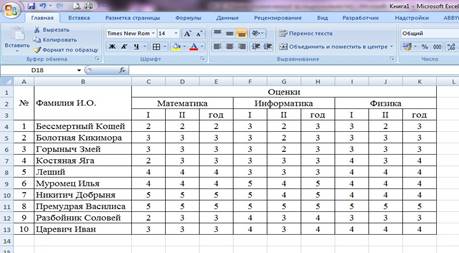
Создать таблицу успеваемости некоторой группы студентов из 20 человек по трем предметам (математике, информатике и физике) за 1, 2 семестр и итоговые, вычислить количество пятерок, четверок, троек и двоек по каждому столбцу оценок:
|
№ |
Фамилия И.О. |
|
Оценки |
|
|
|||||
|
Математика |
Информатика |
|
Физика |
|||||||
|
I |
II |
год |
I |
II |
год |
I |
II |
год |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 2
По созданной таблице построить круговые диаграммы успеваемости за год по каждому предмету с указанием процентного отношения каждой оценки на диаграмме.
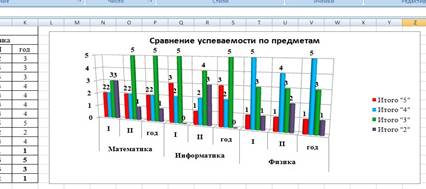
Задание 3
По таблице построить диаграмму сравнения успеваемости по предметам.
Задание 4
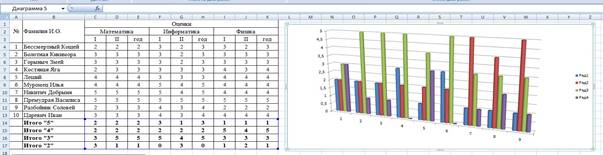
Построить графики успеваемости по каждому предмету.
Порядок выполнения:
1 Создадим таблицу по заданию 1:
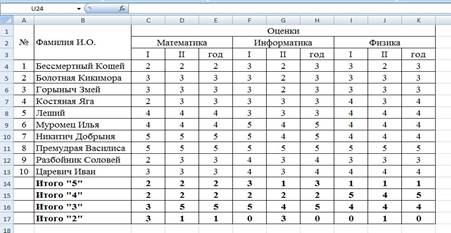
2 Рассчитаем количество оценок по предметам, для этого в ячейке С14 запишем формулу: =СЧЁТЕСЛИ(C4:C13;5). Эта формула считает количество ячеек из заданного диапазона (C4:C13), по заданному условию (=5). Скопируем формулу в остальные ячейки этого столбца, предварительно заморозив строки в диапазоне (C$4:C$13), т.е. копировать будем формулу
=СЧЁТЕСЛИ(C$4:C$13;5). После этого в каждой строке изменим условие, соответственно на 4, 3 и 2. Затем скопируем этот столбец в остальные результаты успеваемости:
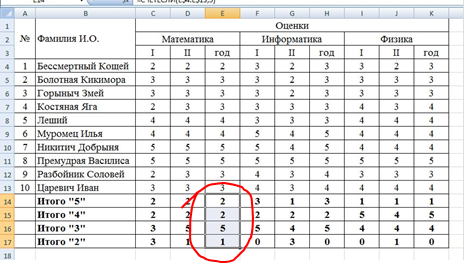
3 В таблице выделим итоги успеваемости по математике:
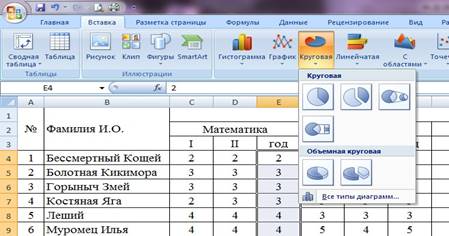
4. В меню вставка выберем Круговая:
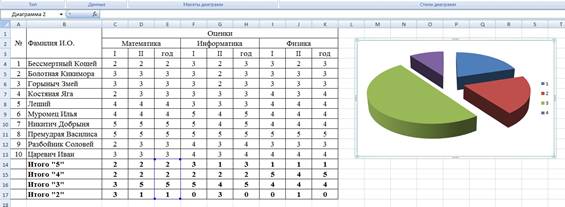
5 Выберем любой из вариантов круговой диаграммы:
6. Оформим диаграмму,
- исправим легенду, открыв контекстное меню легенды, внесем туда содержимое ячеек В14-В17 (раздел «выбрать данные», в правой части «изменить», отметить диапазон ячеек);
- изменим цвета диаграммы (выделить нужный сектор, «формат точки данных» в контекстном меню, «заливка»);
- добавим подписи на элементах диаграммы (выбрать в контекстном меню «формат подписей данных», поставить галочку на нужном разделе, например «доли»);
- добавим заголовок диаграммы (в меню выбрать «макет», «название диаграммы»);
- изменим размер и начертание шрифта:
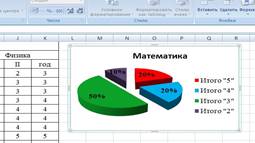
7. Аналогично оформим остальные предметы:
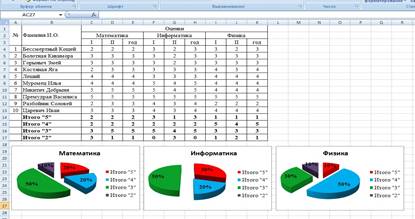
8. Построим гистограмму успеваемости по всем предметам и итогам, для этого выделим ячейки В14 – К17, в меню выберем «гистограмма»:
9 Оформим диаграмму,
исправим легенду;
изменим цвета диаграммы;
добавим подписи на элементах диаграммы;
добавим заголовок диаграммы;
изменим размер и начертание шрифта:
10 Построим графики успеваемости по итогам каждого предмета, для этого выделим ячейки В14 – Е17, в меню выберем «график», выберем данные, оформим диаграммы. 11 В итоге получим:
Порядок выполнения задания, методические указания: - ознакомиться с теоретическими положениями по данной теме; - выполнить задания практической работы; - сформулировать вывод
Содержание отчета: отчет по практической работе должен содержать:
основные определения, рассуждения по выполнению заданий, необходимые изображения, вывод по работе
Компьютерный практикум
Задание 1.
В электронных таблицах построить на листе с данными линейчатую диаграмму отобразить уровень продажи процессоров фирмы Intel за первое полугодие 2013 года.
|
Количество процессоров проданных фирмой Computer LTD (1 полугодие 2013 года) |
||||||
|
|
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
|
Intel Celeron |
78 |
98 |
102 |
120 |
100 |
97 |
|
Intel Core |
110 |
150 |
140 |
148 |
117 |
123 |
|
Intel Xeon |
75 |
83 |
98 |
104 |
80 |
82 |
|
Intel Pentium |
42 |
40 |
46 |
54 |
32 |
30 |
Задание 2.
1. Открыть Лист 2 рабочей книги MS Excel.
2. Внести данные в таблицу.
3. По данным столбцов Источник информации и Названия городов построить гистограмму.
4. По данным столбца Итоги построить круговую диаграмму.
|
Источник информации |
Москва |
С.-Петербург |
Белгород |
Итоги (ср.знач.) |
|
Справочники |
16 |
10 |
8 |
11,33 |
|
Советы знакомых |
56 |
48 |
75 |
59,67 |
|
Телевидение |
60 |
45 |
50 |
51,67 |
|
Радио |
20 |
29 |
12 |
20,33 |
|
Газеты |
29 |
23 |
26 |
26 |
|
Реклама |
5 |
10 |
10 |
8,33 |
|
Объявления |
4 |
6 |
5 |
5 |
|
Советы продавца |
23 |
18 |
20 |
20,33 |
Проанализировать полученные диаграммы и ответить на следующие вопросы внизу листа:
- Укажите три источника информации, которые используют большинство жителей этих городов;
- Укажите два источника информации, которыми пользуются меньше всего жители всех трех городов.
Контрольные вопросы:
1 Что такое диаграмма?
2 Что такое гистограмма и когда используется?
3 Что такое график и когда используется?
4 Что такое круговая диаграмма и когда используется?
5 Что такое линейчатая диаграмма и когда используется?
6 Что такое диаграмма с областями и когда используется?
7 С чего начинается построение диаграммы?
8 Как корректировать диаграмму?
9 Что можно сделать с созданной диаграммой?
3.2.2. Типовые задания для оценки знаний
Теоретический материал
Перечень вопросов к зачету:
1. Функции одной независимой переменной.
2. Пределы
3. Непрерывность функций
4. Производная
5. Исследование функций
6. Неопределенный интеграл
8. Замена переменной.
9. Определенный интеграл
10. Вычисление определенного интеграла
11. Приложение интеграла к решению прикладных задач
12. Задачи, приводящие к дифференциальным уравнениям.
13. Дифференциальные уравнения с разделяющимися переменными
14. Общие и частные решения
15. Однородные дифференциальные уравнения первого порядка
16. Линейные уравнения второго порядка с постоянными коэффициентами
17. Элементы и множества
18. Задание множеств
19. Операции над множествами
20. Свойства операций над множествами
21. Отношения
22. Свойства отношений.
23. Основные понятия теории графов
24. Определение матрицы
25. Действия над матрицами, их свойства
26. Определители второго и третьего порядка, вычисление определителей
27. Определители n-го порядка, свойства определителей
28. Миноры и алгебраические дополнения
29. Разложение определителя по элементам строки и столбца
30. Обратная матрица
31. Элементарные преобразования матрицы
32. Ступенчатый вид матрицы
33. Однородные и неоднородные системы линейных уравнений
34. Определитель системы n линейных уравнений с n неизвестными
35. Правило Крамера для решения квадратной системы линейных уравнений
36. Метод исключение неизвестных – метод Гаусса
37. Определение комплексного числа в алгебраической форме, действия над ними.
38. Геометрическое изображение комплексных чисел
40. Решение алгебраических уравнений.
41. Понятие события и вероятности события
42. Достоверные и невозможные события
43. Классическое определение вероятностей
44. Теорема сложения вероятностей.
45. Теорема умножения вероятностей.
46. Случайная величина
47. Дискретная и непрерывная случайные величины
48. Закон распределения случайной величины.
49. Математическое ожидание случайной величины
50. Дисперсия случайной величины
51. Среднее квадратичное отклонение случайной величины
52. Элементы математической статистики
4. Контрольно-измерительные материалы для итоговой аттестации по учебной дисциплине
Предметом оценки являются умения и знания. Контроль и оценка осуществляются с использованием следующих форм и методов: зачета
Оценка освоения дисциплины предусматривает использование зачетной системы.
I. ПАСПОРТ
Назначение:
КИМ предназначен для контроля и оценки результатов освоения учебной ОП.01 МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ПРИКЛАДНЫХ ПРОФЕССИОНАЛЬНЫХ ЗАДАЧ по специальности 21.02.19 Землеустройство
Умения:
У 1. распознавать и анализировать задачу и/или проблему в профессиональном и/или социальном контексте выделять её составные части и определять этапы решения задачи
У 2. определять необходимые ресурсы и источники информации
У 3. использовать цифровые средства для решения профессиональных задач
У 4. применять современную научную профессиональную терминологию, определять и выстраивать траектории профессионального развития и самообразования
Знания:
З 1. значение математики в профессиональной деятельности;
З 2. основные математические методы решения прикладных задач в области профессиональной деятельности;
З 3. основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
З 4. основы интегрального и дифференциального исчисления.
Вопросы для подготовки по учебной дисциплине выдаются обучающимся в печатном или электронном виде за 14 дней до начала итоговой аттестации по учебной дисциплине.
Типовые задания для проведения экзамена.
- Вычислить определитель
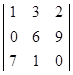 .
. - Даны матрицы
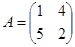 ,
,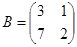 . Найти матрицу 2А-3В
. Найти матрицу 2А-3В - Перемножить матрицы
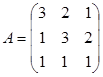 и
и 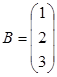 .
. - Перемножить матрицы
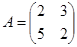 и
и 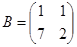 .
. - Решить систему по формулам
Крамера
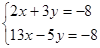
- Решить систему методом Гаусса
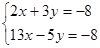
- Записать число z=3-i, в тригонометрической и показательной форме.
- Записать число
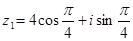 в алгебраической форме.
в алгебраической форме. - Вычислить (4-2i)(1+2i).
- Вычислить
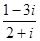 .
. - Найти произведение z1∙z2,
если
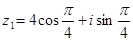 ,
,
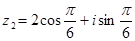 .
. - Выполнить деление чисел
 , если
, если 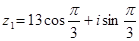 ,
, 
- Найти z3,
если
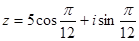 .
. - Извлечь корень
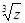 , если
, если 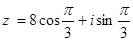 .
. - Вычислить предел
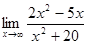 .
. - Вычислить предел
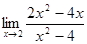 .
. - Вычислить предел
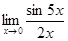 .
. - Найти производную функции y=cosx3
- Найти производную функции y=2x+3lnx.
- Найти производную функции y=3x-4.
- Найти производную функции y=ln5-4x.
- Найти производную функции y=ex(x2-2).
- Найти производную функции y=etqx
- Найти дифференциал функции y=2x-sin2x.
- Найти дифференциал функции
 .
. - Найти производную второго порядка функции y=excosx
- Найти производную второго порядка функции y=x2-2xlnx
- Найти точки максимума (минимума) функции y=x3-12x+1
- Найти
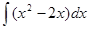 .
. - Найти
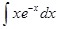 .
. - Найти
 .
. - Найти
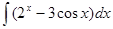 .
. - Найти
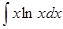 .
. - Найти
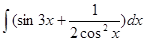 .
. - Вычислить
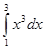 .
. - Вычислить
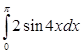 .
. - Вычислить
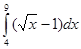 .
. - Вычислить
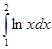 .
. - Вычислить
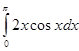 .
. - Вычислить площадь фигуры, ограниченную линиями y=4- x2 и y=0.
- Вычислить площадь фигуры, ограниченную линиями y=x3 , y=8 и y=0.
- Определить объем тела,
образованного вращением фигуры, ограниченной линиями
 , x=1, x=4 вокруг оси OX.
, x=1, x=4 вокруг оси OX. - Определить объем тела, образованного вращением фигуры, ограниченной линиями y=x2, x=0,x=2 вокруг оси OX.
- Определить объем тела, образованного вращением фигуры, ограниченной линиями y=2x-1, x=1,x=3 вокруг оси OX.
- По прогнозу метеорологов вероятность того, что пойдет дождь, равна 0,4, будет ветер – 0,7, будет ветер с дождем – 0,2. Какова вероятность того, что будет дождь или ветер?
- Совет директоров состоит из трех бухгалтеров, трех менеджеров и двух инженеров. Планируется создать подкомитет из его членов. Какова вероятность того, что все трое в этом подкомитете будут бухгалтеры?
- Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не требует внимания рабочего, равна для первого станка 0,9, для второго – 0,8, для третьего -0,85. Найти вероятность того, что в течение часа хотя бы один станок потребует внимания рабочего?
- Случайная величина X распределена по закону
|
49. xi |
50. 0,5 |
51. 1 |
52. 1,5 |
53. 2 |
|
54. pi |
55. 0,2 |
56. 0,3 |
57. 0,4 |
58. 0,1 |
a. Найти математическое ожидание случайной величины Х.
- Случайная величина X распределена по закону
|
60. xi |
61. 1 |
62. 3 |
63. 4 |
|
64. pi |
65. 0,2 |
66. 0, 5 |
67. 0,7 |
a. Найти дисперсию случайной величины Х.
- Для выборки, представленной статистическим рядом
|
69. xi |
70. 10 |
71. 15 |
72. 20 |
73. 25 |
|
74. ni |
75. 4 |
76. 6 |
77. 4 |
78. 2 |
a. определить среднее значение.
- Для выборки, представленной статистическим рядом
|
80. xi |
81. 15 |
82. 16 |
83. 18 |
84. 19 |
|
85. ni |
86. 1 |
87. 4 |
88. 5 |
89. 2 |
a. определить дисперсию.
- В магазин поступило 30 новых телевизоров, среди которых 5 имеют скрытые дефекты. Наудачу отбирается один телевизор для проверки. Какова вероятность того, что он не имеет скрытых дефектов?
- Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три из шести (ничьи во внимание не принимаются)?
ИТОГОВЫЙ ЗАЧЕТ ПО учебной дисциплине ОП.01 МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ПРИКЛАДНЫХ ПРОФЕССИОНАЛЬНЫХ ЗАДАЧ по специальности 21.02.19 Землеустройство
II. ЗАДАНИЕ ДЛЯ ЭКЗАМЕНУЮЩЕГОСЯ. Вариант № 1
Вариант 1
Инструкция для обучающихся
Внимательно прочитайте задание.
Время выполнения задания – 90 мин
Задание
|
Пример задания вариант 1: 1. Понятие комплексного числа, алгебраическая и показательная формы комплексного числа. Умножение комплексных чисел, заданных в алгебраической форме на примере. 2.
Найти А + ВТ, если 3.
Решить систему линейных уравнений методом алгебраического сложения
4.
Вычислить предел функции: 5.
Найти производную функции y = ln 6.
Найти интеграл 7. Найти общее решение дифференциального уравнения: ydx-xdy=0. 8. Фабрика выпускает сумки. В среднем на 120 качественных сумок приходится девять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. |
||
|
|
||
|
Результаты освоения (объекты оценки) |
Критерии оценки результата |
Отметка о выполнении |
|
З 1. значение математики в профессиональной деятельности; З 2. основные математические методы решения прикладных задач в области профессиональной деятельности; З 3. основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; З 4. основы интегрального и дифференциального исчисления. |
- формулировка основных понятий, правил, методов в соответствии с эталоном; - проверка соответствия полученного ответа с эталоном; - выбор методов и способов решения конкретных заданий в соответствии с алгоритмом. - личная оценка качества выполненной работы. |
Да / Нет
Да / Нет
Да / Нет
Да / Нет
Да / Нет |
|
Нарушения при выполнении задания, ответе на вопрос |
Ошибки незначительные (Зачет) |
Ошибки грубые, существенные (Незачет) |
|
Самостоятельность |
Ошибки исправлены без помощи преподавателя |
Ошибки не исправлены, даже с помощью преподавателя |
|
Активность |
Активное участие в решении всех практических задач и(или) в работе группы |
Формальное или пассивное участие в решении практических заданий, не участие в выполнении заданий и(или) в работе группы |
|
Элементы оценивания |
Содержание |
Зачет |
Незачет |
|
Освоение теоретического материала |
Ответ на 2-3 теоретических вопроса Пояснение алгоритма выполнения задания |
Выполнено, выполнено частично (с помощью наводящих вопросов) |
выполнено частично (не смог с помощью наводящих вопросов), или не выполнено |
|
Освоение практических умений |
Выполнение практических заданий |
Выполнено, выполнено частично (не менее 60%) |
не выполнено или выполнено частично (менее 60%) |
Справочный материал: рабочая тетрадь по дисциплине, таблица производных, таблица интегралов
Литература для обучающихся:
1 Основные печатные и электронные издания:
1. Абдуллина, К. Р. Математика: учебник для СПО / К. Р. Абдуллина, Р. Г. Мухаметдинова. — Саратов : Профобразование, 2021. — 288 c. — ISBN 978-5-4488-0941-5. — Текст : электронный // Электронный ресурс цифровой образовательной среды СПО PROFобразование : [сайт]. — URL: https://profspo.ru/books/99917 (дата обращения: 18.11.2020). — Режим доступа: для авторизир. Пользователей
2. Баврин, И. И. Математика для технических колледжей и техникумов : учебник и практикум для среднего образования / Н. В. Богомолов. — 11-е изд., перераб. и доп. — Москва: Издательство Юрайт, 2023. — 326 с. — (Профессиональное образование). — ISBN 978-5-534-08799-4. — Текст: электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/512668
3. Ганичева, А. В. Практикум по математической статистике с примерами в Excel, учебное пособие для спо / А. В. Ганичева, А. В. Ганичев. — 2-е изд., стер. — Санкт-Петербург: Лань, 2022. — 112 с. — ISBN 978-5-8114-9550-4. — Текст : электронный // Лань : электроннобиблиотечная система. — URL: https://e.lanbook.com/book/200444 (дата обращения: 22.06.2022). — Режим доступа: для авториз. пользователей.
.2. Дополнительные источники
1. Электронно-библиотечная система «Лань» – URL: https://e.lanbook.com/
2. Электронно-библиотечная система «Знаниум» – URL: https://znanium.com/
3. Научная электронная библиотека «eLibrary» – URL: https://elibrary.ru/
4. Скачано с www.znanio.ru
© ООО «Знанио»
С вами с 2009 года.
![]()


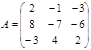 и
и