
Оценочные материалы
Входная контрольная работа по математике для 10 класса (№1)
1. Сократите дробь: ![]() .
.
2. Упростите выражение:![]() .
.
3. Литр бензина стоит 22 руб. Какое наибольшее целое число литров бензина можно приобрести на 700 руб. при повышении цены на 5%?
4. Найдите область определения
выражения: ![]() .
.
5. Решите уравнение:![]() .
.
|
6. На клетчатой бумаге с клетками размером 1
см 7. Решите систему уравнений:
|
|
2 вариант
1. Сократите дробь: ![]() .
.
2. Упростите выражение:![]() .
.
3. Стоимость одной пачки бумаги в магазине равна 240 руб. Какое наибольшее число таких пачек бумаги можно приобрести на 950 руб. при понижении цены на 10%?
4. Найдите область определения
выражения: ![]() .
.
5. Решите уравнение:![]() .
.
|
6. На клетчатой бумаге с клетками размером 1см
|
|
7. Решите систему уравнений: 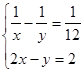 .
.
Контрольная работа№2 по теме «Действительные числа»
Вариант 1
5.
Решите неравенство ![]() .
.
6.
Постройте график функции ![]() .
.
Вариант 2
1. Найдите остаток от деления на 19 числа 671.
2. Запишите периодическую дробь 0,(35) в виде обыкновенной дроби.
3.
Сравните числа ![]() и
и ![]() .
.
4.
Решите уравнение ![]() .
.
5.
Решите неравенство ![]() .
.
6. Постройте
график функции ![]() .
.
Контрольная работа № 3 по теме: «Взаимное расположение прямых в пространстве»

Контрольная работа№4 по теме «Числовые функции»
Вариант 1
1.
Задает ли указанное правило функцию ![]() ,
если:
,
если:
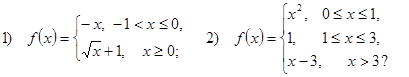
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках ─ 2; 1; 5;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2.
Исследуйте функцию ![]() на четность.
на четность.
3.
![]() периодическая функция с периодом Т
= 3. Известно, что
периодическая функция с периодом Т
= 3. Известно, что
![]()
а) Постройте график функции; б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
4.
Придумайте пример аналитически заданной функции, определенной на
открытом луче ![]() .
.
5.
Известно, что функция ![]() возрастает на R. Решите неравенство
возрастает на R. Решите неравенство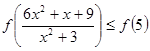 .
.
Вариант 2
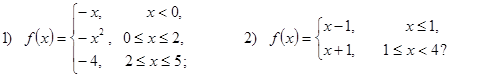
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите
значения функции в точках ![]() ; 2; 6;
; 2; 6;
в) постройте график функции;
г) найдите промежутки монотонности функции.
а) Постройте ее график функции;
б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
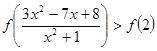 .
.
_______________________________________________________________________
6. Найдите
функцию, обратную функции ![]() . Постройте на
одном чертеже графики указанных двух взаимно обратных функций.
. Постройте на
одном чертеже графики указанных двух взаимно обратных функций.
Контрольная работа № 5. «Параллельность прямых и плоскостей»
Вариант 1
1. Плоскости α и β параллельны, причем плоскость α пересекает некоторую прямую а. Докажите, что и плоскость β пересекает прямую а.
2. Точки А, В, С, D не лежат в одной плоскости, точки К, М, Р — середины отрезков АВ, ВС, CD. Докажите, что плоскость КМР параллельна прямым АС и BD.
3. Даны две параллельные плоскости и не лежащая между ними точка Р. Две прямые, проходящие через точку Р, пересекают ближнюю к точке Р плоскость в точках А1 и А2, а дальнюю — в точках В1 и В2 соответственно. Найдите длину отрезка B1B2, если
А1А2 = 6 см и РА1 : А1В1 = 3:2.
4. Постройте проекцию квадрата ABCD, зная проекции его вершин А, B и точки пересечения диагоналей О: точки A1, B1 и О1.
Вариант 2
1. Прямые а и b параллельны, причем прямая а пересекает некоторую плоскость α. Докажите, что и прямая b пересекает плоскость α.
2. Точки А, В, С, D не лежат в одной плоскости, точки К, М, Р — середины отрезков АВ, AC, AD. Докажите, что плоскости КМР и BCD параллельны.
3. Даны две параллельные плоскости и не лежащая между ними точка К. Две прямые, проходящие через точку К, пересекают ближнюю к точке К плоскость в точках А1 и А2, а дальнюю — в точках В1 и В2 соответственно. Найдите длину отрезка В1В2, если А1А2 = 10 см и КА1 : А1В1 = 2:3.
4. Постройте проекцию правильного треугольника, зная проекции его вершины А и середин К, М сторон АВ и ВС: точки А1, К1 и М1.
Контрольная работа№6 по теме «Тригонометрические функции»
Вариант 1
1.
Центр окружности единичного радиуса совпадает с началом координат
плоскости хОу. Принадлежат ли дуге ![]() точки
М1(-1; 0), М2 (0; -1), М3
точки
М1(-1; 0), М2 (0; -1), М3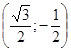 , М4
, М4 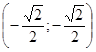 ?
?
2.
Вычислите: ![]() .
.
3.
Вычислите ![]() если
если ![]() .
.
4.
Решите неравенство: а) ![]() б)
б) ![]() .
.
5.
Постройте график функции ![]() .
.
6. Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
![]()
Вариант 2
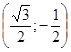 , М2
(0; 1), М3
, М2
(0; 1), М3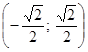 , М4
, М4
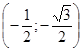 ?
? ![]()
Контрольная работа№7 по теме «Тригонометрические уравнения»
Вариант 1
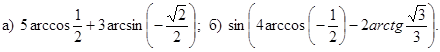
б) ![]() .
.
__________________________________________________
6. Решите систему неравенств:
а) 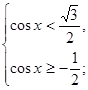
Вариант 2
1.
Вычислите: ![]()
2. Постройте график функции ![]() .
.
3. Решите уравнение: а) ![]()
б)
![]() .
.
4. Найдите корни уравнения ![]() принадлежащие промежутку
принадлежащие промежутку ![]() .
. ![]()
5. Постройте график функции ![]() .
.
__________________________________________________
6. Решите систему неравенств:
а) 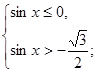
Контрольная работа за 1 полугодие (№8)
Вариант-1
1 часть
1. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?
2. Телефонная компания предоставляет на выбор три тарифных плана.
|
Тарифный план |
Абонентская плата |
Плата за 1 минуту разговора |
|
"Повременный" |
135 руб. в месяц |
0,3 руб. |
|
"Комбинированный" |
255 руб. за 450 мин. в месяц |
0,28 руб. за 1 мин. сверх 450 мин. в месяц. |
|
"Безлимитный" |
380 руб. в месяц |
|
Абонент выбрал наиболее дешевый тарифный план исходя из предположения, что общая длительность телефонных разговоров составляет 700 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 700 минутам? Ответ дайте в рублях.
3. Найдите значение
выражения ![]() .
.
4. Найдите наибольшее
значение функции![]() .
.
5. Найдите ![]() , если
, если ![]() и
и
![]() .
.
6. Найдите ![]() , если
, если ![]() .
.
7. Найдите точку максимума функции, график которой изображен на рисунке
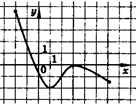 2 часть
2 часть
Решение задач 2 части оформите полностью. Не забудьте записать ответ.
8. а) Решите уравнение 2![]() x – 3 =
x – 3 = ![]() -
-
![]() x. б) Укажите корни, принадлежащие отрезку [ -
x. б) Укажите корни, принадлежащие отрезку [ -![]() ;
;
![]() ].
].
9. Решите неравенство ![]() ≥
≥![]()
Вариант-2
1 часть
1. Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
2. Строительной фирме нужно приобрести 40 кубометров строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.
|
Поставщик |
Цена бруса |
Стоимость доставки |
Дополнительные условия |
|
A |
4200 |
10200 |
|
|
Б |
4800 |
8200 |
При заказе на сумму больше 150 000 руб. доставка бесплатно |
|
В |
4300 |
8200 |
При заказе на сумму больше 200 000 руб. доставка бесплатно |
3. Найдите значение
выражения ![]() .
.
4.Найдите
наименьшее значение функции ![]() .
.
5. Найдите ![]() , если
, если ![]() и
и
![]() .
.
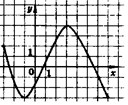 6. Найдите
6. Найдите ![]() , если
, если ![]() .
.
7. Найдите длину промежутка возрастания функции, график которой изображен на рисунке.
2 часть
Решение задач 2 части оформите полностью. Не забудьте записать ответ.
8. а) Решите уравнение 3![]() x – 2 =
x – 2 = ![]() –
–
![]() x.
x.
б) Укажите корни,
принадлежащие отрезку [ -![]() ;].
;].
9. Решите неравенство: ![]() ≤
≤
![]()
Вариант-3
1 часть
1. Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?
2. Строительной фирме нужно приобрести 75 кубометров пенобетона у одного из трех поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей придется заплатить за самую дешевую покупку с доставкой?
|
Поставщик |
Стоимость пенобетона |
Стоимость доставки |
Дополнительные условия |
|
A |
2650 |
4500 руб. |
|
|
Б |
2700 |
5500 руб. |
При заказе на сумму больше 150 000 руб. |
|
В |
2680 |
3500 руб. |
При заказе более 80 м3 |
3. Найдите
значение выражения ![]() .
.
4. Найдите
наибольшее значение функции ![]() .
.
5.
Найдите ![]() , если
, если ![]() и
и ![]() .
.
6.
Найдите ![]() , если
, если ![]() .
.
7. Найдите точку минимума функции, график которой изображен на рисунке.
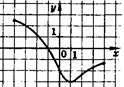
2 часть
Решение задач 2 части оформите полностью. Не забудьте записать ответ.
8. а)
Решите уравнение 4![]() x – 3 =
x – 3 = ![]() –
–
![]() x. б) Укажите корни, принадлежащие отрезку [ -
x. б) Укажите корни, принадлежащие отрезку [ -![]() ;].
;].
9. Решите
неравенство: х2 –3 х + 1 - ![]() ≤
3
≤
3
Вариант-4
1 часть
1. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
2. Для группы иностранных гостей требуется купить 10 путеводителей. Нужные путеводители нашлись в трёх интернет-магазинах. Условия покупки и доставки даны в таблице.
|
Интернет- |
Цена одного |
Стоимость |
Дополнительные условия |
|
А |
283 |
200 |
Нет |
|
Б |
271 |
300 |
Доставка бесплатно, если |
|
В |
302 |
250 |
Доставка бесплатно, если |
3. Найдите значение
выражения ![]() .
.
4. Найдите наименьшее
значение функции ![]() .
.
5. Найдите ![]() , если
, если ![]() и
и
![]() .
.
6. Найдите ![]() , если
, если ![]() .
.
7. Найдите длину промежутка убывания функции, график которой изображен на рисунке.
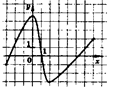
2 часть
Решение задач 2 части оформите полностью. Не забудьте записать ответ.
8. а) Решите уравнение ![]() x – 1 =
x – 1 = ![]() –
2
–
2![]() x. б) Укажите корни, принадлежащие отрезку [ -
x. б) Укажите корни, принадлежащие отрезку [ -![]() ;].
;].
9. Решите неравенство: ![]() +
+
![]() ≥
≥
![]()
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 вариант |
20 |
345 |
2 |
-0,8 |
0,1 |
3 |
3 |
а) πn, -π/4+ πk б)-π, 0, -5π/4, -π/4 |
(-∞;-14] (-4;-1] (5;+∞)
|
|
2 вариант |
34 |
178200 |
-24 |
-2,4 |
0,75 |
2,25 |
4 |
а) πn, π/4+ πk б)-π, 0, π -3π/4, π/4, 5π/4 |
(-3;-1,5] (0,5; +∞) |
|
3 вариант |
1296 |
202500 |
7,5 |
3,7 |
0,2 |
0,25 |
1 |
а) πn, π/4+ πk б)-π, 0, π -3π/4, π/4, 5π/4 |
(-3;0] (1,75; +∞] |
|
4 вариант |
8 |
3010 |
-9 |
1,7 |
1 |
-1 |
2 |
а) π/2+πn, π/4+ πk б)-π/2, π/2, 3π/2 -3π/4, π/4, 5π/4 |
(-∞;0] (1;5/3] (2;3) |
Контрольная работа № 9. «Перпендикулярность прямых и плоскостей»
1 вариант
1. Концы отрезка АВ, не пересекающего плоскость, удалены от нее на расстояния 2,4м и 7,6м. Найдите расстояние от середины М отрезка АВ до этой плоскости.
2. Перекладина длиной 5м своими концами лежит на двух вертикальных столбах высотой 3м и 6м. Каково расстояние между основаниями столбов?
3. Из точки к плоскости проведены две наклонные, равные 17см и 15 см. Проекция одной из них на 4 см больше проекции другой. Найдите проекции наклонных.
4. Из вершины равностороннего треугольника АВС проведен перпендикуляр АМ к плоскости треугольника. Чему равно расстояние от точки М до прямой ВС, если АМ =1м, ВС = 8м?
2 вариант
1. Точка А лежит в плоскости, точка В - на расстоянии 12,5м от нее. Найдите расстояние от плоскости до точки М, делящей отрезок АВ в отношении АМ : МВ = 2 : 3.
2. Какой длины нужно взять перекладину, чтобы ее можно было положить концами на два вертикальных столба высотой 4м и 8м, поставленные на расстоянии 3м один от другого?
3. Из точки к плоскости проведены две наклонные, одна из которых на 6см длиннее другой. Проекции наклонных равны 17см и 7см. Найдите наклонные.
4. Из вершины квадрата АВСК проведен перпендикуляр АМ к плоскости квадрата. Чему равно расстояние от точки М до прямой ВК, если АМ =2м, АВ = 8м?
Контрольная работа №10 по теме «Преобразование тригонометрических выражений»
Вариант 1
1. Докажите тождество:
а) ![]() ,
,
б)
![]() .
.
2. Упростите
выражение 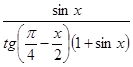 .
.
а) ![]() , б)
, б) ![]() .
.
Вариант 2
1. Докажите тождество:
а) ![]() ,
,
б) ![]() .
.
2. Упростите выражение 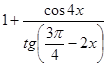 .
.
3. Вычислите ![]() .
.
4. Найдите ![]() .
.
5. Найдите корни уравнения ![]()
принадлежащие промежутку ![]() .
.
6. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
Контрольная работа№11 по теме «Комплексные числа»
Вариант 1
1. Вычислите:
а)![]() , б)
, б)![]() .
.
2. Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки ![]() ;
;
б) множество точек z, удовлетворяющих
условию ![]()
в) множество точек z, удовлетворяющих
условию ![]() .
.
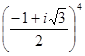 .
. 6. Решите уравнение ![]() .
.
Вариант 2
1. Вычислите:
а)![]() , б)
, б)![]() .
.
2. Изобразите на комплексной плоскости:
а) середину
отрезка, соединяющего точки ![]() ;
;
б) множество точек z, удовлетворяющих условию ![]()
в)
множество точек z, удовлетворяющих условию ![]() .
.
3. Запишите
комплексное число в стандартной тригонометрической форме: а)![]() , б)
, б)![]() .
.
4. Решите
уравнение ![]() .
.
5. Вычислите
![]() .
.
6.
Решите уравнение ![]()
Контрольная работа № 4. «Многогранники»

«Контрольная работа№13 по теме «Производная»
Вариант 1
1. Напишите
первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой ![]() .
.
2. Исследуйте
последовательность ![]() на ограниченность и на
монотонность.
на ограниченность и на
монотонность.
![]() .
.
6.
Напишите уравнение касательной к графику функции ![]() в
точке
в
точке ![]() .
.
Вариант 2
![]()
6.Напишите
уравнение касательной к графику функции ![]() в
точке
в
точке ![]() .
.
Контрольная работа №14 по теме «Применение производной»
Вариант 1
1.
Исследуйте функцию у = ![]() на монотонность и экстремумы.
на монотонность и экстремумы.
2. Постройте график функции у = 3x2 – х3.
3.
Найдите наименьшее и наибольшее
значения функции у = ![]() х3 -
х3 - ![]() х2 + 1 на отрезке [-1; 1].
х2 + 1 на отрезке [-1; 1].
4. В полукруг радиуса 6 см вписан прямоугольник. Чему равна наибольшая площадь прямоугольника?
Вариант 2
Контрольная работа № 15 по теме: «Векторы»

Контрольная работа №16 по теме «Комбинаторика и вероятность»
Вариант 1
1. Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов?
2. Сколько четырехзначных чисел можно составить из цифр 1,2,3,4 при условии, что каждая цифра может содержаться в записи числа лишь нечетное число раз?
3. Решите уравнение ![]() .
.
4. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом 2 туза?
5. На прямой взяты 8 точек, а на параллельной ей прямой – 5 точек. Сколько существует треугольников, вершинами которых являются данные точки?
Вариант 2
1. В яхт-клубе состоит 9 человек. Из них надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?
2. Сколько четырехзначных чисел можно составить из цифр 1,2,3,0 при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
3. Решите
уравнение ![]() .
.
4. Из колоды в 36 карт вытаскивают три карты. Какова вероятность того, что все они тузы?
5. Сколько существует треугольников, у которых вершины являются вершинами данного выпуклого 8-угольника, но стороны не совпадают со сторонами этого n-угольника?
Итоговая контрольная работа
Вариант 1
1. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 40 руб. за штуку. У Вани есть 450 руб. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?
2. Футболка стоила 500 рублей. После снижения цены она стала стоить 390 рублей. На сколько процентов была снижена цена на футболку?
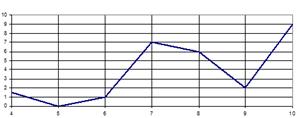
3. На рисунке изображен график осадков в г.Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм. Определите по графику, сколько дней из данного периода осадков выпало между 2 и 8 мм.
4. Строительной
фирме нужно приобрести ![]() кубометров пенобетона. У неё есть 3 поставщика.
Сколько рублей придется заплатить за самую дешевую покупку с доставкой? Цены и
условия доставки приведены в таблице
кубометров пенобетона. У неё есть 3 поставщика.
Сколько рублей придется заплатить за самую дешевую покупку с доставкой? Цены и
условия доставки приведены в таблице
|
Поставщик |
Стоимость пенобетона (р. за м3 ) |
Стоимость доставки |
Дополнительные условия |
|
A |
|
|
|
|
Б |
|
|
При заказе на сумму больше |
|
В |
|
|
При заказе более |
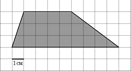
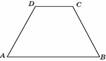
5. На клетчатой
бумаге с клетками размером 1 см ![]() 1 см изображена трапеция (см. рисунок). Найдите
ее площадь в квадратных сантиметрах.
1 см изображена трапеция (см. рисунок). Найдите
ее площадь в квадратных сантиметрах.
6. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
7. Найдите корень
уравнения ![]() .
.
8. В треугольнике ![]() угол
угол ![]() равен
равен ![]() ,
, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
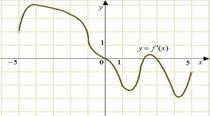
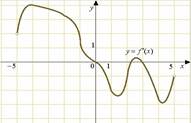
9. На рисунке
изображен график производной функции ![]() ,
определенной на интервале
,
определенной на интервале ![]() . В какой точке отрезка
. В какой точке отрезка ![]()
![]() принимает наибольшее значение.
принимает наибольшее значение.
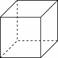
10. Объем куба равен 8. Найдите площадь его поверхности.
11. Два велосипедиста одновременно отправляются в 154 -километровый пробег. Первый едет со скоростью на 3 км/ч большей, чем второй и прибывает к финишу на 3 ч раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
12. Найдите точку
минимума функции ![]() .
.
Часть 2
С 1 Решите уравнение ![]()
Вариант 2
!. Аня купила месячный проездной билет на автобус. За месяц она сделала 45 поездок. Сколько рублей она сэкономила, если проездной билет стоит 750 рублей, а разовая поездка 19 рублей?
2. Шариковая ручка стоит 30 рублей. Какое наибольшее число таких ручек можно будет купить на 700 рублей после повышения цены на 25%?
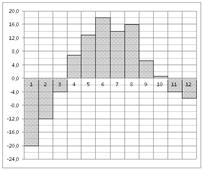
3. На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году.
4. Семья из трех
человек едет из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно —
на своей машине. Билет на поезд стоит ![]() рублей на одного человека. Автомобиль расходует
рублей на одного человека. Автомобиль расходует ![]() литров бензина на 100
километров пути, расстояние по шоссе равно 700
км, а цена бензина равна
литров бензина на 100
километров пути, расстояние по шоссе равно 700
км, а цена бензина равна ![]() руб. за литр. Сколько рублей придется заплатить за
наиболее дешевую поездку на троих?
руб. за литр. Сколько рублей придется заплатить за
наиболее дешевую поездку на троих?
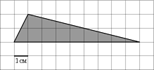
5. На клетчатой
бумаге с клетками размером 1 см ![]() 1 см изображен треугольник (см. рисунок). Найдите
его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите
его площадь в квадратных сантиметрах.
6. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
7. Найдите корень
уравнения ![]() .
.
8. В треугольнике ![]() угол
угол ![]() равен
равен ![]() ,
, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
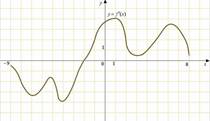
9. На рисунке
изображен график производной функции ![]() ,
определенной на интервале
,
определенной на интервале ![]() . В какой точке отрезка
. В какой точке отрезка ![]()
![]() принимает наибольшее значение.
принимает наибольшее значение.
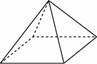
10. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
11. Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
12. Найдите точку
максимума функции ![]() .
.
Часть 2
С1 Решите уравнение ![]() .
.
Вариант3
1. В летнем лагере 219 детей и 28 воспитателей. В автобус помещается не более 48 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город?
2. Цена на электрический чайник была повышена на 16% и составила 2320 рублей. Сколько рублей стоил товар до повышения цены?
3. Посев семян тыквы
рекомендуется проводить в мае при дневной температуре воздуха не менее ![]() °
С. На рисунке показан прогноз дневной температуры воздуха в первой и второй
декадах мая. Определите, в течение скольких дней за этот период можно
производить посев тыквы.
°
С. На рисунке показан прогноз дневной температуры воздуха в первой и второй
декадах мая. Определите, в течение скольких дней за этот период можно
производить посев тыквы.

4. Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 600 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?
|
Автомобиль |
Топливо |
Расход топлива на 100 км |
Арендная плата за 1 сутки |
|
1. |
Дизельное |
|
|
|
2. |
Бензин |
|
|
|
3. |
Газ |
|
|
Цена дизельного
топлива ![]() р. за литр, бензина
р. за литр, бензина ![]() р. за литр, газа
р. за литр, газа ![]() р. за литр.
р. за литр.
5. На клетчатой
бумаге с клетками размером 1 см ![]() 1 см изображена фигура (см. рисунок). Найдите ее
площадь в квадратных сантиметрах. В ответе запишите
1 см изображена фигура (см. рисунок). Найдите ее
площадь в квадратных сантиметрах. В ответе запишите ![]() .
.

6. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
7. Найдите корень
уравнения: ![]()
8. Меньшее основание равнобедренной трапеции равно 6. Высота трапеции равна 10. Тангенс острого угла равен 2. Найдите большее основание.
9. На рисунке
изображен график производной функции ![]() ,
определенной на интервале
,
определенной на интервале ![]() . Найдите количество точек
экстремума функции
. Найдите количество точек
экстремума функции ![]() на отрезке
на отрезке ![]() .
.
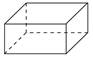
10. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
11. Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.
12. Найдите точку
максимума функции ![]() .
.
Часть2
С 1 . Решите уравнение ![]()
Вариант 4
1. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 45 руб. за штуку. У Вани есть 300 руб. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?
2. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?
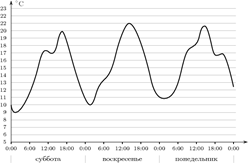
3. На графике показано изменение температуры воздуха в некотором населённом пункте на протяжении трех суток, начиная с 0 часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.
4. Семья из трех
человек едет из Москвы в г.Чебоксары. Можно ехать поездом, а можно — на
своей машине. Билет на поезд стоит ![]() рублей на одного человека. Автомобиль расходует
рублей на одного человека. Автомобиль расходует ![]() литров бензина на 100
километров пути, расстояние по шоссе равно 700
км, а цена бензина равна
литров бензина на 100
километров пути, расстояние по шоссе равно 700
км, а цена бензина равна ![]() руб. за литр. Сколько рублей придется заплатить за наиболее
дешевую поездку на троих?
руб. за литр. Сколько рублей придется заплатить за наиболее
дешевую поездку на троих?
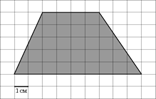
5. На клетчатой
бумаге с клетками размером 1 см ![]() 1 см изображена трапеция (см. рисунок). Найдите
ее площадь в квадратных сантиметрах.
1 см изображена трапеция (см. рисунок). Найдите
ее площадь в квадратных сантиметрах.
6. В соревнованиях по толканию ядра участвуют 9 спортсменов из Греции, 3 спортсмена из Болгарии, 10 спортсменов из Румынии и 8 — из Венгрии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Болгарии.
7. Найдите корень
уравнения: ![]() Если уравнение имеем более одного корня, укажите
меньший из них.
Если уравнение имеем более одного корня, укажите
меньший из них.
8. В треугольнике ![]() угол
угол ![]() равен
равен ![]() ,
, ![]() ,
, ![]() . Найдите
. Найдите ![]() .
.
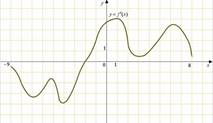
9. На рисунке
изображен график производной функции ![]() ,
определенной на интервале
,
определенной на интервале ![]() . Найдите точку экстремума
функции
. Найдите точку экстремума
функции ![]() на интервале
на интервале ![]() .
.
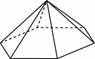
10. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
11. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 154 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 ч. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
12. Найдите наибольшее значение функции y=x3–12x+7 на отрезке [−3;0].
Часть 2
С 1 Решите уравнение ![]()
Ответы итоговой контрольной работы в 10 классе
|
вар |
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
В8 |
В9 |
В10 |
В11 |
В12 |
С1 |
|
1 |
11 |
22 |
3 |
93100 |
19,5 |
0,995 |
60 |
0,6 |
-1 |
24 |
11 |
0 |
|
|
2 |
105 |
18 |
3 |
1540 |
9 |
0,93 |
16 |
0,75 |
6 |
340 |
13 |
-4 |
|
|
3 |
6 |
2000 |
4 |
4018 |
8 |
0,25 |
-14 |
16 |
3 |
4 |
9 |
0 |
|
|
4 |
5 |
20 |
10 |
945 |
32,5 |
0,1 |
7 |
15 |
-2 |
200 |
14 |
23 |
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.