Министерство науки и высшего образования РФ

Самарский колледж строительства и предпринимательства (филиал)

Федерального государственного бюджетного образовательного учреждения

высшего образования

 «Национальный исследовательский Московский государственный

строительный университет»

 

 

 

 

Курс лекций

 по дисциплине «Основы геодезии»

для студентов специальности 08.02.01

Строительство и эксплуатация зданий и сооружений

 

 

 

 

 

 

 

 

 

 

 

 

Самара,

2021 г.

Рассмотрен Предметно-цикловой комиссией Председатель ПЦК_______ И.А. Тышковская Протокол № __ от «__»_____2021 г.

Одобрен Зам. директора по УП и НМР _____________Ю.И. Дудникова __ от «__»_____2021 г.

 

 

 

 

Утвержден

Зам. директора по УВР

_________________О.В. Панова

«___»_________2021 г.

 

 

                                                

Разработчики: 

Заборникова И.В. – преподаватель высшей квалификационной категории

и предпринимательства (филиала) ФГБОУ ВО «НИУ МГСУ»

Подробный курс лекций составлен в соответствии с рабочей программой по дисциплине «Основы геодезии» для специальности 08.02.01 Строительство и эксплуатация зданий и сооружений.

Темы разбиты на лекции, после некоторых идут разобранные задачи и вопросы для самопроверки.

 

 

 

 

 

 

 

 

 

 

Содержание

№ п/п	Название темы	№ страницы
1	Общие сведения о геодезии. Масштабы. Картографические условные знаки	4
2	Рельеф местности	19
3	Ориентирование направлений. Прямая и обратная геодезические задачи	39
4	Сущность геодезических измерений. Классификация и виды. Линейные измерения	49
5	Геодезические измерения. Угловые измерения	58
6	Геометрическое нивелирование	78
7	Геодезические съемки. Теодолитный ход. Полевые и камеральные работы. Понятие о тахеометрической съемке	97
8	Содержание и технология работ по полевому трассированию	108
9	Построение профиля по результатам трассирования	113
10	Список использованных источников	118

 

ТЕМА 1

ОБЩИЕ СВЕДЕНИЯ О ГЕОДЕЗИИ.

МАСШТАБЫ. КАРТОГРАФИЧЕСКИЕ УСЛОВНЫЕ ЗНАКИ

·        ОБЩИЕ СВЕДЕНИЯ О ГЕОДЕЗИИ.

Геодезия – это наука об измерениях на поверхности земли и математической обработке этих измерений.

Геодезия решает научные и практические задачи. К числу научных задач геодезии относятся:

- определение разности уровня морей;

- определение формы и размеров всей земли;

- определение внешнего гравитационного поля земли;

- наблюдение за деформациями земной коры. К числу практических задач геодезии относятся:

- определение координат и отметок точек земной поверхности в единой системе координат;

выполнение геодезических измерений с целью построения карт, планов, профилей;

- обеспечение геодезическими данными другие отрасли хозяйства.

В связи с многообразием решаемых задач геодезия делится на ряд самостоятельных дисциплин:

-                     высшая геодезия (изучение фигуры Земли и ее внешнего гравитационного поля, определение геодезических координат отдельных точек земной поверхности);

-                     топография (изучение изображения сравнительно небольших участков земной поверхности);

-                     фотограмметрия (изучение объектов фотографирования по фотоснимкам);

- космическая геодезия (изучение поверхности земли по снимкам из космоса);

- морская геодезия (изучение прибрежных участков суши);

- аэрофото геодезия (изучение земли по аэроснимкам);

- картография (изучение и составление карт планов, атласов)

- инженерная геодезия – разрабатывает методы геодезических работ, выполняемых при изысканиях, проектировании, строительстве и эксплуатации разнообразных инженерных сооружений, установке и монтаже специального оборудования, с целью разведки, использования и эксплуатации природных богатств

Задачи инженерной геодезии заключаются в следующем:

1) получение геодезических материалов, необходимых для составления проекта работ по строительству сооружения, путем выполнения полевых геодезических измерений и вычислительно-графических работ;

2) определение на местности положения основных осей и границ сооружений и других характерных точек их в соответствии с проектами строительства;

3) обеспечение геометрических форм и размеров элементов сооружения на местности в соответствии с его проектом в процессе строительства;

4) обеспечение геометрических условий установки и наладки специального оборудования;

5) установление отклонений сооруженного объекта от его проекта («исполнительные съемки»);

6) изучение деформаций основания и тела сооружения, происходящих под действием различных нагрузок, под влиянием внешних факторов и деятельности человека;

7) определение расположения на поверхности Земли (или в ее недрах) отдельных объектов, элементов и характеристик, представляющих интерес для данного вида или отрасли народного хозяйства.

Инженерно-геодезические работы, имеющие прикладное значение, являются наиболее обширными. Инженерная геодезия использует методы высшей геодезии, топографии и фотограмметрии, а в отдельных случаях и свои приемы и средства.

 

·        ПОНЯТИЕ О ФОРМЕ И РАЗМЕРАХ ЗЕМЛИ

Мысль о том, что Земля имеет форму шара, впервые высказал в VI. Веке до н.э. древнегреческий ученый Пифагор, а доказал это и определил радиус Земли египетский математик и географ Эратосфен, живший в IIIвеке до н.э. Впоследствии ученые уточнили, что Земля сплюснутая у полюсов. Такая фигура в математике называется эллипсоидом вращения, получается от вращения эллипса вокруг малой оси.

Земля не является правильным геометрическим телом – ее поверхность представляет собой сочетание возвышенностей и углублений. Большая часть углублений заполнена водой океанов и морей. Поверхность воды под действием силы тяжести образует уровенную поверхность, перпендикулярную в каждой точке направлению силы тяжести. Линию, совпадающую с направлением силы тяжести, называют отвесной линией. Если уровенную линию продолжить мысленно под материками, образуется фигура, называемая геоидом (рис.1.1.) (уровенной поверхностью называется поверхность морей и океанов мысленно продолженную по суше).

 

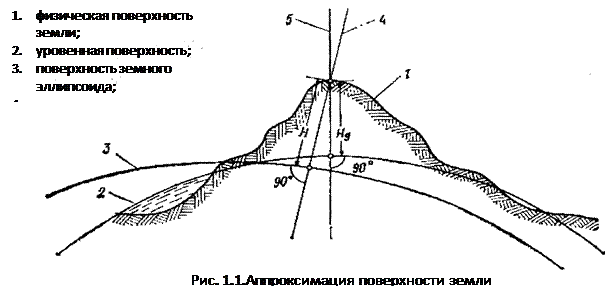
Поверхность геоида не может быть представлена достаточно простым уравнением и неудобна для обработки результатов геодезических измерений, так как геоид имеет неправильную форму. С геометрической точки зрения математическая фигура приближенная к геоиду называется эллипсоид (это фигура образованная эллипсом при вращении его вокруг малой полуоси)

В каждой стране применяют свой эллипсоид максимально приближенный к геоиду данного государства и тогда такой эллипсоид называется референц-эллипсоидом.

В нашей стране принят референц – эллипсоид Красовского с размерами: а=6387 км ; b=6356 км ; α=(a – b)/a = 1/298,3.

В некоторых случаях при геодезических измерениях, выполняемых на довольно значительных участках поверхности земли, геоид принимают за шар с R= 6371,11 км, эквивалентным по объему референц-эллипсоиду. Участки земной поверхности площадью менее 20 км2 можно считать плоскостью при измерении углов и расстояний.

Где а и b большая и малая полуоси эллипсоида, α –полярное сжатие.

 

 

 

 

 

 

 

 

 

 

 

 

·        ПОНЯТИЕ КАРТЫ, ПЛАНА, ПРОФИЛЯ

При изображении физической поверхности Земли на картах её проектируют на поверхность эллипса, а затем его разворачивают в плоскость. Таким образом, картой называют уменьшенное и закономерно искаженное изображение Земли или отдельных частей её поверхности на плоскости.

Иначе поступают с изображением плана. Физическую поверхность Земли ортогонально проектируют на горизонтальную плоскость. Таким образом, планом называют уменьшенное и подобное изображение ортогональной проекции местности, в пределах которой кривизна уровенной поверхности не учитывается Ортогональная проекция – изображение пространственного объекта на плоскости посредством проектирующих лучей, перпендикулярных к плоскости проектирования. Длина ортогональной проекции линии на горизонтальную плоскость называется горизонтальным проложением. По назначению топографические карты и планы делятся на основные и специализированные. К основным относятся карты и планы общегосударственного картографирования. Эти материалы многоцелевого назначения, поэтому на них отображают все элементы ситуации и рельефа. Специализированные карты и планы создают для решения конкретных задач отдельной отрасли. Так, дорожные карты содержат более детальную характеристику дорожной сети. К специализированным относят и изыскательские планы, используемые только в период проектирования и строительства зданий и сооружений. На этих картах только часть нумерованных объектов изображаются точно, все остальные – схематически. Кроме планов и карт к топографическим материалам относят профили местности, представляющие собой уменьшенное изображение вертикального разреза земной поверхности вдоль выбранного направления. Профили местности являются топографической основой при составлении проектно-технической документации, необходимой при строительстве подземных и наземных трубопроводов, дорог и других коммуникаций.

На топографических картах все объекты земного изображаются максимальной точностью, независимо от значимости объекта.

Стандартные масштабы

Масштабы топокарт:  Масштабы планов:

1:100000   1:5000

1:50000  1:2000

1:25000  1:1000

1:10000   1:500

 

·        МАСШТАБЫ

Отношение длины линии на плане к длине горизонтального проложения этой линии на местности называется численным масштабом топографического плана. Его обычно представляют в виде правильной дроби, числитель которой равен единице, а знаменатель – некоторому числу N, показывающему, во сколько раз расстояние на плане ab уменьшено по сравнению с соответствующим горизонтальным проложением Ао Во линии местности.

Так, при аЬ=5см и АоВо=250м имеем

  (1.1)

При сравнении численных масштабов различных планов употребляют термины: «мельче» и «крупнее». Если N1 < N2, то есть знаменатель первого масштаба меньше знаменателя второго, то говорят, что первый масштаб крупнее второго, или второй масштаб мельче первого. Для удобства численный масштаб часто записывают в виде пояснительного масштаба, например: «в 1 сантиметре 50 метров».

Линейный масштаб используют для измерения с небольшой точностью длин отрезков на плане. Он представляет собой прямую линию, разделенную на равные отрезки. Длина одного отрезка называется основанием масштаба. Она соответствует определенному числу метров на горизонтальном проложении. На рисунке 1.3 основание принято равным 2см, что при численном масштабе 1:5000 соответствует 100м на горизонтальном проложении. Левое крайнее основание линейного масштаба разделено на более мелкие деления.

 

Рис.1.3 Линейный масштаб

Поперечный масштаб применяют для измерений и построений повышенной точности. Для каждого масштаба можно построить свой поперечный масштаб. Поперечный масштаб с основанием 2см называется нормальным сотенным поперечным масштабом, то есть пригодным для любого масштаба.

Поперечный масштаб строят следующим образом:

На прямой линии откладывают ряд отрезков по 2см, которые называют основанием масштаба. Из концов оснований восстанавливают перпендикуляры произвольной длины. На крайних перпендикулярах измерителем откладывают по 10 отрезков одинаковой длины и соединяют их концы. Крайнее левое основание сверху и снизу делят на 10 одинаковых частей методом деления отрезка на пропорциональные части. Затем соединяют верхние и нижние точки (рис. 1.4)

 

	Рис.1.4. Поперечный масштаб

 

 

Для пользования поперечным масштабом необходимо мысленно оцифровать его деления исходя из масштаба плана или карты. Так если масштаб плана 1:5OO, то основанием равно 10м деление равно 1 м и наименьшее деление 01м.

Измеритель располагают таким образом, чтобы правая игла находилась на одной из вертикальных линий, а левая на трасверсале. После чего считают, сколько целых (к), десятых (п) и сотых (i) долей основания содержится между углами и исходя из ранее выполненной оцифровки, вычисляют расстояние.

 

 

S=к(АВ)+п(0,1АВ)+1(0,01АВ) (1.2.)

Для случая приведенного на рис. 1.5 имеет к=1; п=4; i=3,5 масштаб 1:500, а следовательно:

S=1*100+4(0,1 *100)+3,5(0,01 *100)=143,5м

Невооруженный глаз человека способен на чертеже, на расстоянии 20-25см увидеть точку равную 0,1мм. Поэтому точностью масштаба называют длину горизонтальной проекции на местности, соответствующую 0,1мм на карте или плане. Для масштаба 1:500; 1:1000; 1:10000; 1:25000; точность масштаба соответственно равно 0,05м; 0,1м; 1,0м; 2,5м.

 

Примеры

Пример 1. Дано расстояние между двумя точками на карте равное 56,4мм. Определить длину горизонтального проложения соответствующей линии местности, если масштаб карты равен 1:2000.

Решение. Вычисление производится по формуле

Sm=SP*M,

где - знаменатель численного масштаба, показывающий во сколько раз линии местности уменьшены при их изображении на карте;

 - длина линии на плане или карте;

Sm – горизонтального проложения соответствующий линии на местности.

SP=56,4мм, то Sm=56,4мм*2000=112800мм=112,8м

Пример 2. Дано горизонтальное проложение линий местности равное 78,0м. Определить с точностью 0,1 мм длину соответствующей линии на карте в масштабе 1:2 000

 

Решение. Вычисление выполняют по формуле:

 

 

=78,0м=78000мм, то =78000:2000=39,0мм на карте масштаба 1:2000.

Пример 3. Определить длину отрезка на плане масштаба 1:1000, если длина линии на местности равна 35.6м.

Решение:

Так же как и в предыдущей задаче необходимо мысленно оцифровать деления поперечного масштаба. Так, если масштаб плана 1:1000, то основание поперечного масштаба равно 20 м., АВ=2м и наименьшее деление (а1 в1) равно 0.2м. А затем суммированием этих отрезков набрать длину линии на поперечном масштабе. Т.е.35.6:20м =1 (целое основание масштаба). Осталась длина линии 15.6. Ее делим на цену деления основания масштаба 15.6:2м=7 (целых делений основания масштаба. 7х2м=14м. 15.6-14м=1.6м. 1.6м:0.2м=8 (наименьших делений масштаба). После этого устанавливаем измеритель на поперечном масштабе так, чтобы между иголками измерителя уложилось 1 целое основание масштаба, 7 целых целений основания масштаба и 8 наименьших делений масштаба.

Пример 4.На карте масштаба 1:2000 был измерен отрезок, длинной 2.5 см. Найти длину линии на местности, соответствующую этому отрезку.

 

 

 

Решение.

Так как задан численный масштаб 1:2000 значит в этом масштабе 1см. на карте соответствует 2000 см. или 20 м на местности, тогда в 2.5см будет 2.5х20=50м . Ответ: 50м.

Пример 5. Найти длину отрезка на плане масштаба 1:500, если длина горизонтального проложения линии на местности 28.50м.

Решение:

В масштабе 1:500 1см на плане соответствует 5м на местности. По условию задачи на местности 28.5м. Следовательно

1 основание -10м

1 деление – 1м

1 наименьшее деление – 0,1м

Ответ: 2осн.+8дел.+5н.дел

Пример 6. Определить точность масштаба 1:10 000.

Решение. Так как точность масштаба это длина горизонтальной проекции линии на местности, соответствующая 0.1мм на карте или плане, необходимо вычислить длину линии на местности, соответствующую 0.1мм на карте или плане. По аналогии с предыдущими задачами рассуждаем так 1см на карте масштаба 1:10 000 соответствует 100м на местности, соответственно

1мм –10м,

0.1мм – 1м

Ответ: 1м.

Пример 7: Перевести численный масштаб 1:10000 в пояснительный.

Решение: Для перевода численного масштаба в пояснительный необходимо от сантиметров в знаменателе перейти к метрам;

1/10000:100 или 1 см-100 м.

 

·        СОДЕРЖАНИЕ ПЛАНОВ И КАРТ. УСЛОВНЫЕ ЗНАКИ ПЛАНОВ И КАРТ

Местные предметы на топографических планах и картах изображаются условными топографическими знаками. Изображаемые на планах объекты местности можно разбить на две группы. Одна группа по своим размерам может выражаться в масштабе данной карты или плана, как, например, пашни, луга, леса, огороды, моря, озера и т.п. Предметы другой группы по своим размерам не могут быть выражены в масштабе карты, например, ширина дорог, малых рек, ручьев, мосты, указатели дорог, километровые столбы, колодцы, родники, геодезические знаки, различные ориентиры.

Условные знаки для первой группы предметов называются масштабными, или контурными, для второй группы – внемасштабными.

·                   Масштабные знаки изображают предметы подобными оригиналу, и по ним можно определить размеры и форму предметов (пашни, леса, сенокосы, кустарники, пастбища, сады, огороды). Контуры обозначаются точечными пунктиром, а внутреннее содержание отражают условными знаками

·                   Линейные условные знаки используют для изображения объектов линейного типа, длина которых выражается в масштабе (дороги, реки, линии электропередач). Ширина таких объектов меньше точности масштаба данной карты.

·                   Внемасштабные условные знаки применяют для изображения предметов (колодцы, геодезические знаки, родники, столбы и т.п.). Внемасштабные условные знаки показывают только положение объекта, отображающие их характер и назначение, но по ним нельзя судить об их размерах.

·                   Пояснительные условные знаки дополняют другие условные знаки цифровыми данными, пояснительными надписями и т.п., характеризующими предметы местности (грузоподъемность и ширина мостов, порода деревьев, средняя высота, толщина и расстояние между деревьями в лесу, ширина дорог, отметка урезов воды в водоеме и т.п.).

 

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1.                 Что изучает геодезия?

2.                 Виды геодезии?

3.                 Какие задачи решает инженерная геодезии?

4.                 Что представляет собой действительная фигура Земли?

5.                 Почему изображение фигуры Земли заменяют референц-эллипсоидом или шаром?

6.                 Что такое уровенная поверхность?

7.                 Что называется планом?

8.                 Что называется картой?

9.                 В чем отличия между картой и планом?

10.            Что называется профилем местности?

11.            Что называется масштабом?

12.            Что представляют собой численный и пояснительный масштабы?

13.            Перечислите масштабы топографических карт и планов.

14.            Что такое точность масштаба?

15.            Как построить нормальный сотенный поперечный масштаб?

16.    Что называется контурными знаками?

17.   Что называется внемасштабными знаками?

18.   Что называется линейными знаками?

19.   Что называется поясняющими знаками?

20.   Приведите примеры условных знаков: контурных (масштабных), линейных, внемасштабных, поясняющих.

 

 

 

 

 

 

ТЕМА 2 РЕЛЬЕФ МЕСТНОСТИ

·        ИЗОБРАЖЕНИЕ РЕЛЬЕФА НА ТОПОГРАФИЧЕСКИХ КАРТАХ И ПЛАНАХ

Совокупность неровностей земной поверхности называют рельефом. Рельеф играет значительную роль в деятельности человека. Его учитывают при проектировании строительства, преобразуют в формы, удобные для эксплуатации сооружения. Правильное освоение и использование территорий невозможно без учета рельефа.

На топографических картах рельеф изображается в виде горизонталей. Суть метода горизонталей состоит в том, что поверхность земли сечется плоскостями параллельными уровенной поверхности.

 

 

 

 

 

Горизонталь – след пересечения секущей плоскости с поверхности земли. Понятие о горизонтали можно получить, если представить себе местность, затопленную до заданной высоты. Береговая линия в этом случае будет горизонталью. Изменяя уровень воды (высоту уровенной поверхности) получим горизонтали с различными высотами.

Высота точки – это расстояние по нормали от точки на поверхности земли до уровенной поверхности, принятой за отчетное численное выражение высоты называется отметкой (Н). За начало отсчета в нашей стране принят средний уровень Балтийского моря, который отмечен в виде футштока (медная полоса, укрепленная на одном из устоев обводного канала в г. Кронштадт) Разность отметок двух точек называется превышением h,

h = HК-HН.

 

 

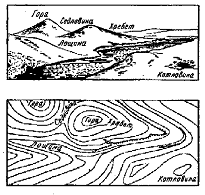
На картах и планах высоты горизонталей изменяются через равные промежутки. Разность высот соседних горизонталей называют высотой сечения рельефа, а расстояние между горизонталями на плане – заложением. Высоту сечения рельефа выбирают в зависимости от масштаба карты или плана и характера местности. Стандартные высоты сечения рельефа: 0.25; 0.5; 1.0; 2.0; 2.5; 5.0; 10.0м. В пределах данного плана или карты высота сечения рельефа постоянна. Только в местах со сравнительно большим расстоянием между горизонталями и для рисовки деталей рельефа в необходимых местах проводятся пунктирными линиями полугоризонтали. Для вычерчивания горизонталей используют светло-коричневую тушь (сиену жжоную), которая закрывает ситуацию, обычно изображаемую черным цветом.

Горизонтали подписывают на планах и картах в разрывах основанием в сторону понижения ската местности. Кроме отметок горизонталей на картах подписывают отметки характерных точек рельефа (вершины горы, дна котловины и т.д.). Направление склона местности показывается у горизонталей бергштрихами – черточками, проводимыми в сторону понижения местности. Бергштрихи выставляются не у всех горизонталей, но в количестве достаточном для чтения рельефа.

·        СВОЙСТВА ГОРИЗОНТАЛЕЙ

1) бергштрихи направлены в сторону понижения;

2) основания цифр, которыми подписаны горизонтали, располагаются в направлении понижения ската;

3) к водоемам и водотокам местность понижается;

4) в одну сторону от горизонтали местность повышается, а в другую понижается;

5) горизонтали перегибаются на водораздельных линиях хребтов и тальвегах лощин;

6) отметка точки на горизонтали равна отметке горизонтали;

7) отметки горизонталей всегда кратны высоте сечения рельефа.

8)горизонталь – это всегда замкнутая кривая, никогда не пересекается.

·        ОСНОВНЫЕ ФОРМЫ РЕЛЬЕФА.

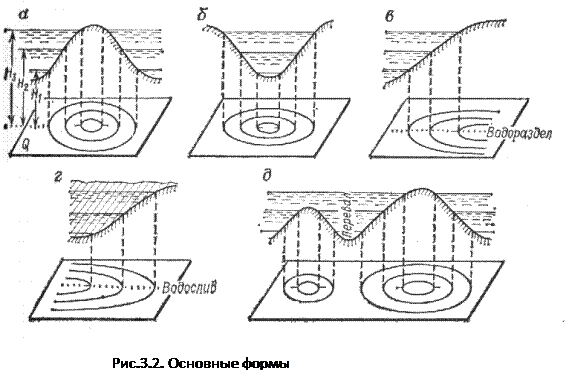
Несмотря на кажущееся разнообразие рельефа, выделяют 5 основных форм:

1. Гора, холм — возвышающаяся над окружающей местностью часть земной поверхности (Рис.3.2а). Наивысшую точку горы называют вершиной, низ — подошвой, а боковые поверхности — скатами.

2. Котловина, впадина — замкнутое углубление поверхности (рис.3.2.б). Наиболее низкую часть впадины называют дном, боковые поверхности — скатами, а линию слияния с окружающей местностью — бровкой.

3. Хребет — вытянутая в одном направлении возвышенность со скатами в двух противоположных направлениях (рис. 3.2, в). Линию встречи скатов в верхней части называют водоразделом.

4. Лощина — вытянутое в одном направлении понижение с двумя скатами (Рис.3.2г). Линию встречи скатов в нижней их части называют водосливом.

5. Седловина — понижение между двумя возвышенностями (Рис.3.2.д). Наиболее низкую точку между возвышенностями называют перевалом.

·        РЕШЕНИЕ ИНЖЕНЕРНО ГЕОДЕЗИЧЕСКИХ ЗАДАЧ НА КАРТАХ И ПЛАНАХ

 

Решение инженерно-геодезических задач рассмотрим на примерах.

1 Определение отметок точек.

Пример 1: Определить отметки точки А и В, hc=1м

 

 

 

 

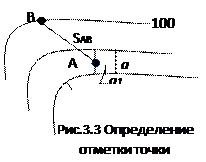
Решение: Для определения отметки точки А необходимо определить отметки горизонталей между которыми находится точка А; провести перпендикуляр через точку между двумя соседними горизонталями. С помощью линейки измерить расстояние а и а1. Составить пропорцию и найти х.

, отсюда

Примечание: а и а1 измеряются либо в сантиметрах, либо в миллиметрах (в метры не переводятся).

Для рис.3.3 получим а=0,6см; а1=0,3см, тогда

Высота точки А определяется:

; НА=98,00м+0,50м=98,50м

Результат округляется до 0,01.

Точка В находится на горизонтали поэтому ее отметка будет равна высоте горизонтали (НВ=100м).

2.Определение превышения между точками.

Пример 2: Определить превышение между точками А и В.

Решение: Превышение это разность конечной точки и начальной точки между точками А и В определится:

Из примера 1 получим hАВ=100,00м-98,50м=1,50м

3. Определение высоты сечения

Пример 3: Определить высоту сечения карты.

Решение: Для того чтобы определить высоту сечения рельефа необходимо найти подписанные горизонтали и сосчитать количество промежутков между горизонталями. Высота сечения определяется по формуле: ,

 

 

 

 

 

 

 

где - отметки соответственно старшей горизонтали(с большей отметкой) и младшей горизонтали (с меньшей отметкой);

- количество промежутков между горизонталями.

Ответ: высота сечения равна 1м.

 

4. Определение уклона линии

 

 

 

 

Для численной характеристики крутизны ската на местности используют угол наклона n0 или уклон i. Уклоном линии местности называют отношение превышения к горизонтальному проложению. Из прямоугольного треугольника АВС следует:

 

, (3.2)

 

где h – высота сечения рельефа,

а – заложение

Из формулы следует, что уклон безразмерная величина. Его выражают или в процентах %(сотых долях), или в промиллях (тысячных долях), а угол наклона в градусах.

Пример 4: Определить уклон линии АВ.

Решение: Уклон линии АВ равен:

 

 

 

 

 

 

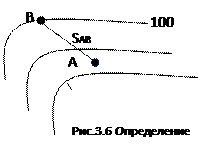
 и  были определены в примере 2.  - горизонтальное проложение между точками А и В. Оно измеряется линейкой и переводится в масштаб карты или плана. Если масштаб карты 1:1000, то = 29м

 

 

 

 

 

 

5. Построение горизонталей аналитическим методом.

Решение: Аналитический метод связан с вычислением расстояний от закрепленной точки до горизонтали. Сущность этого метода иллюстрируется на рис 3.7.

Пусть линия 5-6¾проекция линии 5-6¢ местности на горизонтальную плоскость в данном масштабе. Точки 5 и 6 — соседние точки. Пусть отметка точки 5 равна Н5, а точки 6 равна Н6. Н1,Н2,Н3- отметки секущих горизонтальных плоскостей с отметками кратными высоте сечения рельефа. Горизонтальное проложение линии 6-5 равно d. Из решения подобных прямоугольных треугольников имеем

 

  

 

Приведем численный пример. Н5=56.19м, Н6=55.36м., высота сечения равна 0,25м. Между этими отметками пройдут горизонтали с отметками Н1=55.50, Н2=55.75, Н3=56.00м. Горизонтальное проложение d= 40мм. Тогда

d1=40(0.14/0.83)=6.7мм

d2=40(0.39/0.83)=18.8мм

d3=40(0.64/0.83)=30.8мм

Отложив от вершины 6 по стороне 6-5 отрезки, равные 6.7, 18.8 и 30.8 мм получим положение горизонталей с отметками 57.50, 57.75 и 56.00 м. Интерполируя аналогично между остальными отметками, найдем положение этих же горизонталей. Соединив точки с одинаковыми отметками точки плавной линией, получим горизонтали.

6. Построение горизонталей графическим методом.

Решение: Графический метод интерполирования заключается в нахождении положения горизонталей с помощью прозрачной палетки. Для этого на листе кальки проводят параллельные линии через равные расстояния (обычно через 5 или 10 мм). Находят на плане вершину с наименьшей отметкой и, ориентируясь на нее, подписывают линии палетки отметками, кратными высоте сечения рельефа (hс=0.25 м).Например, Нmin=54.79 м. Следовательно, параллельные линии оцифровываются снизу вверх, начиная с отметки 54.75 м (при hс=0.25 м). . д.

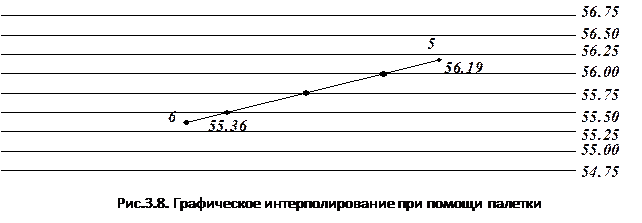
Далее: 55.00; 55.25; 55.50 и т. Д.

 

 

Для интерполирования по линии 5-6 накладывают палетку на план так, чтобы точка 5 заняла положение между линиями с отметками 56.00 и 56.25 соответственно своей отметке 56.19 м (рис.3.8). В точке 5 иглой измерителя прокалывают кальку и поворачивают ее вокруг иглы так чтобы точка 6 расположилась между линиями с отметками 55.25 и 55.50 соответственно своей отметке 55.36. Закрепив в этом положении палетку, осторожно прокалывают остро отточенным карандашом пересечения линий 55.50, 55.75 и 56.00 с линией сетки квадратов 5-6. Аналогичным образом производится интерполирование и по другим отметкам. Соединив точки с одинаковыми отметками плавными линиями, получим горизонтали.

 

6 Построение продольного профиля линии

Построить продольный профиль и вычислить уклон линии на карте

Решение:

Линия АВ, по которой должен быть построен профиль называется профильной, а соединяющая точки А и В – воздушной линией.

Данная задача встречается при камеральном трассировании линейных сооружений, например газопровода. Для проектирования и строительства таких сооружений необходимо иметь продольный профиль – вертикальный разрез линии по заданной линии.

Построение профиля осуществляется следующим образом.

1.                 На миллиметровой бумаге проводят прямую линию, являющуюся основанием профиля.

2.                 На основание профиля переносят с карты точки пересечения профильной линии с горизонталями, водоразделами, тальвегами, седловинами и вершинами, выписывая в соответствующую графу (рис.3.9) их отметки.

3.                 В полученных точках восстанавливают перпендикуляры и откладывают на них высоты в вертикальном масштабе, который принимают в 10 раз крупнее горизонтального. Для того чтобы чертеж был компактный, все отметки уменьшают на одинаковое число метров, которое называется условным горизонтом (на чертеже 110 м). Его выбирают таким образом, чтобы точка профиля с наименьшей отметкой располагалась на 2-3 см выше основания профиля.

 

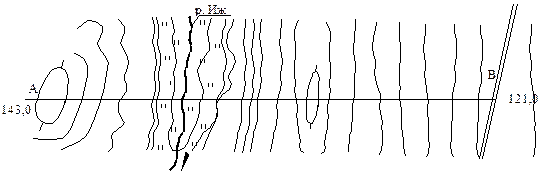
Соединив концы перпендикуляров, получают профиль.

Уклон воздушной линии можно получить по формуле:

                                            iAB=(HB-HA)/SAB, (5.3)

 

где SAB – горизонтальное проложение линии АВ, выраженное в метрах.

4.                 В графу ‘’план трассы’’ переносят с карты ситуацию, имеющуюся в обе стороны от оси трассы на расстоянии 1см. Линии, соединяющие точки A и В как на плане так и на профиле, а также в графе уклонов, проводят красным цветом.

5.                 Ситуацию вычерчивают цветом, соответствующим ее изображению на карте.

 

 

Вопросы для самопроверки:

1.                 Что называется рельефом местности?

2.                 Дайте определение основным формам рельефа, назовите их характерные точки или линии.

3.                 Что называется горизонталью?

4.                 Перечислите основные свойства горизонталей.

5.                 Что такое бергштрих, полугоризонталь, высота сечения рельефа, заложение горизонталей?

6.                 Изобразите горизонталями основные типовые формы рельефа. Покажите характерные точки или линии основных форм рельефа.

7.                 Что называется высотой точки?

8.                 Что называется абсолютной, условной, относительной высотой точки?

9.                 Что называется уклоном линии местности?

10.            Как по карте определить высоту точки и уклон линии местности?

11.            Как по заложению определить крутизну ската?

 

 

 

 

 

 

 

 

 

 

ТЕМА 3 ОРИЕНТИРОВАНИЕ НАПРАВЛЕНИЙ. ПРЯМАЯ И ОБРАТНАЯ ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИ

·        СИСТЕМА ГЕОГРАФИЧЕСКИХ КООРДИНАТ

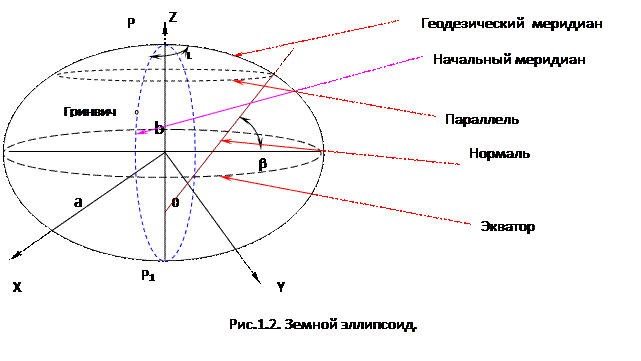
Система географических координат, определяет положение точки на сферической поверхности она применяется на топографических картах для изображения больших участков земной поверхности. Географические координаты бывают:

-геодезические (определяют положение точки относительно эллипсоида);

-астрономические(определяют положение точки относительно геоида).

Отклонение размеров эллипсоида от геоида имеет значение 150м. Эта величина не существенна для измерений на поверхности земли.

В данной системе координатами точки являются широта, долгота, высота, а координатными линиями являются параллель меридиан.

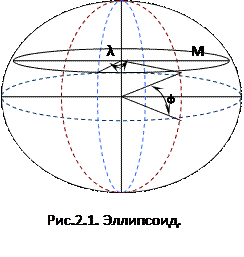
Параллель – это след пересечения эллипсоида плоскостью проходящей через данную точку местности перпендикулярно малой полуоси. За нулевую параллель принят экватор.

Меридиан – это след пересечения эллипсоида плоскостью проходящей через малую полуось эллипса и данную точку местности. За нулевой меридиан принят Гринвичский меридиан.

Широта (φ) – это угол, образованный нормалью данной точки к плоскости эллипсоида и плоскостью экватора.

Долгота (λ) – это двугранный угол образованный плоскостью нулевого гринвичского меридиана и плоскостью меридиана в данной точке (М)

Широта и долгота полностью не отражают положение точки в пространстве необходимо знать 3-ю координату – высоту. Высота рассматривается далее в лекциях.

 

 

 

 

 

 

 

 

 

 

 

 

·        СИСТЕМА ПРЯМОУГОЛЬНЫХ КООРДИНАТ

Система прямоугольных координат зональная, т.е. в каждой зоне начало прямоугольных координат своё. Основными координатными линиями служат две взаимно перпендикулярные линии с началом координат в точке 0. У вертикальной оси абсцисс Х (осевой меридиан), совмещенной с меридианом, положительное направление с юга на север, у горизонтальной оси ординат Y (экватор) положительное направление — с запада на восток. Четверти системы координат имеют названия, соответствующие сторонам света и нумеруются по часовой стрелке от северо-восточной четверти, (рис. 2.5) На листах топографических карт и планов прочерчивается координатная сетка (километровая).

 

 

 

 

 

 

 

 

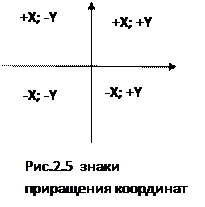
·        ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ НА ТОПОГРАФИЧЕСКИХ КАРТАХ.

Положение точки на плоскости определяется координатами Х и Y со знаком «+» или «-», зависящими от четверти.(рис. 2.8а)

 

Так, координаты точки M равны +Xm, +Ym, а точка N имеет координаты –Xn, -Yn.

Определяют масштаб карты и разбиваются с оцифровкой сетки координат.

Выделяют квадрат километровой сетки, в котором находится точка, и выписывают координаты его (рис 2.8б) юго-западного угла.(Ха=6074; Yа=4311)

Из т.А опускают перпендикуляры на стороны квадрата километровой сетки.

С помощью измерителя и поперечного масштаба определяют длины перпендикуляров относительно юго-западного угла.(∆Ха; ∆Yа)

Вычисляют координаты т.А:

 

 (2.2)

 

Недостатком изложенного способа является его бесконтрольность. Здесь любая грубая ошибка в изменении останется незамеченной. Поэтому на практике измеряют не только отрезки XA и YA , но и продолжения их до северной и восточной сторон километровой сетки, т.е. X¢A¢ и Y¢A . Очевидно, что при отсутствии погрешностей в измерениях должны выполняться условия:

 

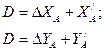 (2.3)

 

Где D – длина стороны квадрата километровой сетки.

Практически таких равенств не получается из-за случайных и систематических погрешностей измерений (деформация бумаги, неточность установки игл измерителя в вершине, погрешности построения поперечного масштаба и т.д.). Однако величина неравенства не должна превышать 0.3 мм в масштабе карты. Если условие выполняется, то

Окончательные координаты точки A можно вычислить по формулам:

 

;

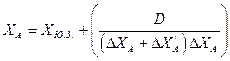   (2.4)

;

·        УГЛЫ ОРИЕНТИРОВАНИЯ.

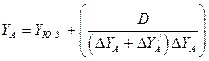Ориентировать линию на местности — значит определить ее положение относительно другого направления, принятого за исходное. В качестве исходных в геодезии используют следующие направления (рис.2.10): северное направление АИ истинного (географического) меридиана; северное направление АМ магнитного меридиана.

Для ориентирования линий на местности служат азимуты, дирекционные углы и румбы.

Азимутом линии называют угол, отсчитываемый от северного направления меридиана по ходу часовой стрелки до ориентируемой линии. Азимут А называют истинным, если он отсчитывается от истинного меридиана и магнитным Ам, если он остсчитывается от магнитного меридиана.

Так как магнитная ось Земли отклонена от оси вращения Земли примерно на 12°. Под влиянием этого фактора между направлениями географического и магнитного меридианов на поверхности Земли образуется угол δ. Этот угол называют склонением магнитной стрелки и отсчитывают от истинного меридиана к магнитному. Восточному склонению приписывают знак плюс, западному — знак минус.

Магнитное склонение в различных точках Земли имеет вековые, годичные и суточные периодические изменения. Суточные изменения в средней полосе достигают 15'. В некоторых районах, где колебания достигают особо больших значений, вообще нельзя пользоваться для ориентирования магнитной стрелкой. Такие районы называют аномальными, например, район Курской магнитной аномалии.

 

 

Рис.2.10 Ориентирование линии на местности

 

Сведения о магнитном склонении можно получить на метеостанции или выбрать из схемы, приведенной под южной рамкой топографической карты.

Сближением меридианов называют угол отсчитываемый от истинного меридиана к осевому меридиану. Восточному сближению приписывают знак плюс, западному — минус.

 Сближение меридианов можно выбрать со схемы под южной рамкой топографической карты или вычислить по формуле

γ=∆λsinφ,  (2.5)

где ∆λ –разность долгот географического меридиана точки и осевого меридиана зоны;

φ – широта точки.

Горизонтальный угол, образованный северным направлением истинного меридиана и данной линии местности отсчитав по ходу часовой стрелки, называется истинным азимутом (рис.2.11.)

 

  (2.6)

 

γ – сближение меридианов

В геодезии принято ориентировать линии по осевому меридиану. Горизонтальный угол, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до линии местности называется дирекционным углом (обозначается буквой a).

a- дирекционный угол изменяется от 0 до 360 градусов.

 (2.7.)

 

·        СВЯЗЬ МЕЖДУ УГЛАМИ ОРИЕНТИРОВАНИЯ

γГ – Гауссово сближение меридиана

δ-склонение магнитной стрелки- это угол,образованный северным направлением истинного и магнитного меридиана. Склонение магнитной стрелки – величина непостоянная даже для одной точки местности. Она изменяется в течение суток, года, века. Сближение и склонение магнитной стрелки указано внизу карты.

γА = (LA – Lo)sinBA  (2.8.)

LA- долгота т.А

Lo – долгота осевого меридиана зоны

BA- широта т.А

Ам = α +γ-δ (2.9.)

 

·        СВЯЗЬ МЕЖДУ ДИРЕКЦИОННЫМ УГЛОМ И РУМБОМ

Румб-это острый угол, отсчитываемый от ближайшего направления (северного или южного) до ориентируемой линии. Величина румба сопровождается названием из двух букв, обозначающих страны света и указывающих направление линии: СЗ : 43о11, ЮВ : 12о15’ и так далее.

 

2.9 Связь между дирекционным углами и прямоугольными координатами

 

Пусть АВ- линия на местности для которой известны координаты т. А и т. В. Необходимо Определить дирекционный угол aАВ и расстояние между точками.

Решение задания начинается с нахождения приращений координат (рис 2.19).

 

 (2.10)

Обе разности координат будут иметь знаки «+» (рис.2.20)

Определение румба выполнится по формуле:

tg r= ∆y/∆x (2.11)

 

В первой четверти дирекционный угол будет равен румбу. Горизонтальное положение между точками А и В определяется по формулам

 

 

S=∆x/cos a; S=∆y/sin a (2.12)

 

·        СВЯЗЬ МЕЖДУ ДИРЕКЦИОННЫМИ УГЛАМИ И ГОРИЗОНТАЛЬНЫМИ УГЛАМИ

Пусть имеем две стороны хода АВ и ВС (рис.2.21). Дирекционный угол aАВ стороны АВ будем считать известным. Если правый по ходу угол обозначить βn, то

  (2.13)

Подставляя значение  из формулы(2.7), получим

 

   (2.14)

 

Если бы мы имели при т.В не правый, а левый угол βл, то получили бы формулу:

 

  .  (2.15)

 

Пример N°1. Дирекционный угол линии АВ равен 165°. Найти румб.

Решение: По формулам взаимосвязи азимутов и румбов получим

 

 

 

 

Пример N°2. Определить дирекционный угол линии АВ, если Аu=60°30’; γ =+0°10’.

Решение: Дирекционный угол линии АВ равен

 

 

 

Пример N°3. Определить величину угла β, если даны дирекционные углы линий aОА=30°00'; aов=135°00'

Решение:

Угол β составит:

β=135°00'-30°00'=105°00'

Пример №4. Вычислить дирекционный угол a2-3 и её румб, если a1-2=60° β2прав=140°

 

 

 

 

 

 

Решение:

 

 

Из рисунка видно:

 тогда

 

 

 

 

 

 

 

 

 

 

 

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

 

Что такое широта и долгота?

Как по карте определить географические координаты точки?

Что представляет собой зональная система прямоугольных координат?

Как по карте определить прямоугольные координаты точки?

Что называется ориентированием линии на местности?

Что называется истинным азимутом линии местности?

Что называется магнитным азимутом линии местности?

Что называется дирекционным углом линии местности?

Как связаны между собой углы ориентирования?

На сколько отличаются прямой дирекционный угол от обратного?

Как перейти от дирекционного угла к румбу?

Как с помощью транспортира измерить на карте дирекционный угол линии местности?

Как связаны дирекционные углы и горизонтальные углы?

Как связаны дирекционные углы и прямоугольные координаты?

 

 

 

 

 

 

 

 

 

 

ТЕМА 4: СУЩНОСТЬ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ. КЛАССИФИКАЦИЯ И ВИДЫ. ЛИНЕЙНЫЕ ИЗМЕРЕНИЯ

Геодезия относится к таким областям техники, где измерения являются необходимым элементом производственной деятельности. И не только необходимым, но таким массовым в своем исполнении, что и вообразить себе невозможно. Достаточно сказать, например, что для съёмки местности площадью всего в 1 га в масштабе 1:500 (для сравнительно средней сложности местности) понадобится около 200 точек, для каждой из которых определяются три координаты: две плановые (х, у) и высота (Н).

Измерения в геодезии являются количественной и качественной основой для изучения Земли, отдельных ее фрагментов, для получения исходной информации при решении всех инженерно-геодезических задач и выполнения топографических работ. Любое измерение выражается количественной характеристикой (величиной угла, длиной линии, превышением, площадью участка местности и т.п.) и имеет качественную сторону, которая характеризует точность полученного результата.

Величины, которые получают в процессе производства геодезических работ, можно классифицировать на измеренные и вычисленные. В первом случае величину получают обычно непосредственно, путем сравнения её с единицей средства измерения, или косвенно, как функцию двух или нескольких непосредственно измеренных величин. Например, площадь прямоугольника может быть получена как произведение его сторон, измеренных непосредственно.

 

 

 

 

 

 

·        РЕЗУЛЬТАТЫ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ

Под результатом геодезического измерения подразумевается конечный результат, который получается в процессе всех произведённых измерений и вычислений. Например, конечным результатом может быть высота точки, её плановые координаты, площадь участка и т.п.

Результаты геодезических измерений в своей группе могут быть равноточными и неравноточными. Если измерения выполнены прибором одного и того же класса точности, по одной и той же методике (программе), в одинаковых внешних условиях, одним и тем же наблюдателем (либо наблюдателями одной квалификации), то такие измерения относят к равноточным. При несоблюдении хотя бы одного из перечисленных выше условий результаты измерений классифицируют как неравноточные.

Примером равноточных измерений могут являться результаты измерений длины одной и той же линии либо линий, примерно равных друг другу, полученные при неизменных условиях внешней среды, одним и тем же измерительным средством (прибором), одними и теми же исполнителями работ, по общей для всех результатов измерений программе.

Если в процессе измерений длины линии, например, светодальномером, изменится температура окружающего воздуха, влажность, давление, то это может привести к получению части неравноточных результатов в общей группе результатов измерений, поскольку при изменении внешних условий может произойти и изменение характеристик измерительного прибора, характеристик прохождения светового луча в атмосфере.

Число измеренных величин и число измерений может быть необходимым и избыточным. При измерении, например, углов в треугольнике число необходимых измеренных величин равно двум, в семиугольнике – шести. Значение третьего (седьмого) угла можно вычислить по сумме двух (шести) измеренных углов. Если необходимо решить плоский треугольник, то дополнительно к измеренным двум углам обязательным является знание длины хотя бы одной из его сторон, в связи с чем число необходимых измеренных величин должно быть равно трём (одно измерение – линейное, два – угловые). Та же задача решается и при выполнении двух линейных измерений и одного угла, заключённого между измеренными сторонами треугольника.

Таким образом, числом необходимых измеренных величин является минимально необходимое их число, при котором обеспечивается решение поставленной задачи. Число же измеренных величин, превышающих число необходимых, называется числом избыточных величин. В геодезии, принято, но и не только принято, а является обязательным, получать и избыточные величины, что обеспечивает обнаружение грубых погрешностей и промахов, позволяет повысить точность результатов измерений. Поэтому в треугольнике, например, обязательно измеряют все три угла и сравнивают полученную сумму углов с теоретической.

Если сформулировать задачу с точки обеспечения заданной точности измерений, то необходимое число измерений должно обеспечивать заданную точность измерения одной величины или самого результата измерений. Так, в том же треугольнике, каждый из его углов может быть измерен несколько раз. Все избыточные измерения повышают надёжность результатов, а также их точность, но в то же время и увеличивают объём работ, и часто прирост увеличения точности становится экономически нецелесообразным из-за большого числа измерений. Иногда говорят, что числом необходимых измерений, например, горизонтального угла, является одно измерение, остальные – избыточные. Это не всегда так, поскольку, одно измерение не позволяет производить оценку точности и может содержать неконтролируемую грубую погрешность (промах).

·        ВИДЫ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ

При геодезических работах основной объём информации получают с помощью геодезических измерений, которые классифици­руются следующим образом:

-         по назначению;

-         по точности;

-         по объёму;

-         по характеру получаемой ин­формации;

-         по инструментальной природе получаемой информации;

-         по взаимозависимости результатов измерений.

 

По своему назначению геодезические измерения бывают:

-         уг­ловые;

-         линейные;

-         нивелирные (измеряются высоты или превыше­ния);

-         координатные (измеряются координаты или их приращения);

-         гравиметрические (измеряют ускорения силы тяжести).

 

В связи с этим сформировались следующие технологические процессы топографо-геодезических работ:

-         топографическая съёмка

-         разбивочные работы

-         определение деформаций зданий, сооружений, земной коры

-         триангуляция

-         трилатерация

-         полигонометрия

-         спутниковые измерения

-         астрономические определения

-         гравиметрические работы

-         створ­ные измерения

 

В зависимости от типов используемых средств геодезические измерения делят на три группы:

-         высокоточные

-         точные (средней точности)

-         технические (малой точности)

 

Процесс измерения в геодезии осуществляется при наличии пяти составляю­щих (факторов):

1.     объект — что измеряется

2.     субъект — кто измеряет

3.     средство — чем измеряется

4.     метод — как измеряется

5.     внешняя среда — в каких условиях и где измеряется.

 

Конкретное содержание и состояние факторов геодезического измерения оп­ределяются условиями, которые могут быть классифициро­анны по следующим признакам:

По Физическому Исполнению:

-         прямые измерения, в которых значение измеряемой вели­чины получают непосредственным сравнением с однородной физической величиной (эталоном). Примером прямого измерения служит измерение длины линии рулеткой или мерной лентой;

-         косвенные измерения, в которых значение определяемой величины по­лучают из вычислений, в которых в качестве исходных используют результаты измерений величин, связанных с определяемой. Например: измерение длины линии светодальномером. В этом случае измеряется непосредственно время прохождения светового сигнала от дальномера до отражателя и обратно, а затем вычисляется длина линии.

По Роду:

-         однородные (измерения однородных физи­ческих величин)

-         разнородные (все прочие по отношению к однородным)

По Количеству:

-         необходимые измерения дают только по одному значению каждой измеряемой величины

-         дополнительные или избыточные измерения производятся для получения нескольких значений измеряемой величины в целях контроля, исключения грубых погрешностей или повышения ка­чества результатов измерений

По Точности:

-         равноточные, которые выполняются в одинаковых услови­ях, т. Е. объекты одного и того же рода измеряют исполнители одинаковой квалификации, приборами одного класса, по единой методи­ке, в достаточно схожих по характеру условиях внешней среды

-         неравноточными считаются измерения, выполняемые в случаях, когда по крайней мере одна из составляющих процесса измерения существенно отличается от аналогичной составляющей других измерений

 

По Физической Природе Носителей Информации:

-         визуальная фиксация результатов измерения, когда переда­ча информации в системе «прибор — цель» осуществляется с учас­тием наблюдателя (оператора);

-         невизуальные измерения в основе своей полностью или час­тично исключают участие наблюдателя. В этом случае используют средства радиоэлектроники, микропроцессорной тех­ники и др.

По Взаимозависимоcти:

-         независимые

-         зависимые

-         коррелированные

 

 

·        ЛИНЕЙНЫЕ ИЗМЕРЕНИЯ. ОСНОВНЫЕ ПАРАМЕТРЫ И РАЗМЕРЫ.

Рулетки следует изготовлять со шкалами номинальной длины 1, 2, 3, 5, 10, 20, 30, 50, 100 м. По заказу потребителя рулетки допускается изготовлять со шкалами иной длины.

Рулетки следует изготовлять с лентами из нержавеющей стали (в условном обозначении – Н) или углеродистой стали (в условном обозначении – У).

Вытяжные концы рулеток следует изготовлять:

- с кольцом (в условном обозначении – буква «К»);

- с грузом (в условном обозначении – буква «Г»).

Рулетки до 5 м включительно допускается изготовлять с вытяжным концом в виде:

- прямоугольного торца (в условном обозначении – буква «П»);

- с держателем для закрепления на предмете, подлежащем измерению (в условном обозначении – буква «Д»).

Условное обозначение рулеток должно включать: букву «Р» - «рулетка», номинальную длину шкалы, материал ленты, класс точности, конструктивное исполнение вытяжного конца ленты и обозначение настоящего стандарта.

Примеры условных обозначений:

Рулетка со шкалой номинальной длины 30 м, лентой из нержавеющей стали, 2-го класса точности, кольцом на вытяжном конце ленты:

Р30Н2К ГОСТ 7502-98

Рулетка со шкалой номинальной длины 5 м, лентой из углеродистой стали, 3-го класса точности, прямоугольным торцом на вытяжном конце ленты:

Р5У3П ГОСТ 7502-98

Технические требования

Рулетки должны соответствовать требованиям настоящего стандарта и конструкторской документации на рулетки конкретных марок, утвержденной в установленном порядке.

 По требованию потребителя изготовитель проводит компарирование заказанных рулеток в соответствии с нормативными документами.

Компарируемым рулеткам присваивают заводской номер. В свидетельстве о поверке указывают действительную длину (по эталону) от нулевого до каждого метрового штриха рулетки с округлением до десятых долей миллиметра.

Рулетки должны быть работоспособными при температуре окружающего воздуха от минус 40 до плюс 50 ˚С и относительной влажности до 98 % при температуре плюс 25 ˚С, а рулетки, поставляемые шахтам, - при температуре от минус 10 до плюс 35 ˚С и относительной влажности до 100 % при температуре плюс 35 ˚С (исполнение УХЛ, категории размещения 1 и 5 по ГОСТ 15150).

Полный средний ресурс для рулеток с лентами из нержавеющей стали – 2000 циклов, рулеток с лентами из углеродистой стали – 1500 циклов (цикл включает в себя: вытягивание ленты на полную длину, натяжение рабочим усилием, отсчет, наматывание ленты).

Критерием предельного состояния (отказом) считают: поломку корпуса и механизма наматывания, заедание, разрыв, стирание штрихов и цифр измерительной ленты свыше 10 % от общего количества штрихов и цифр. Шкалу наносят на один или оба края ленты. Допускается наносить шкалы на обе стороны ленты. Шкалы рулеток наносят с миллиметровыми, сантиметровыми и метровыми интервалами.

Рулетки изготовляют с началом шкалы, совпадающим с торцом измерительной ленты. Рулетки с вытяжным кольцом длиной 10 м и более, изготовляют с началом шкалы, удаленным от торца не менее чем на 100 мм.

Для рулеток с грузом началом шкалы служит нижний торец груза.

За начало отсчета при оцифровке следует принимать:

- для сантиметровых интервалов – начало каждого метра;

- для метровых интервалов – начало шкалы рулетки.

Для сантиметровых интервалов допускается принимать за начало отсчета начало каждого дециметра, при этом оцифровку интервалов, кратных 10, указывают в количестве сантиметровых интервалов от начала каждого метра.

Для сантиметровых интервалов шкал рулеток длиной до 5 м включительно за начало отсчета допускается принимать начало шкалы рулетки без нанесения цифровых обозначений метровых интервалов.

Ширину штриха следует выбирать из ряда: 0,20; 0,30; 0,40 мм. Допускаемое отклонение 0,05 мм.

Штрихи различных интервалов шкалы должны быть разной длины.

 

ТЕМА 5: ГЕОДЕЗИЧЕСКИЕ ИЗМЕРЕНИЯ. УГЛОВЫЕ ИЗМЕРЕНИЯ

·        ПРИНЦИП ИЗМЕРЕНИЯ ГОРИЗОНТАЛЬНОГО УГЛА

Углы обычно измеряют в градусной мере (градусы, минуты, секунды), реже – в радианной. За рубежом широко применяется градовая мера измерения углов.

При геодезических работах измеряют не углы между сторонами на местности, а их ортогональные (горизонтальные) проекции, называемые горизонтальными углами. Так, для измерения угла АВС, стороны которого не лежат в одной плоскости, нужно предварительно спроектировать на горизонтальную плоскость точки А, В, и С и измерить горизонтальный угол abc = β 

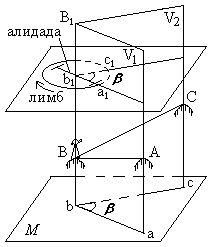
Принцип измерения горизонтального угла

Рассмотрим двугранный угол между вертикальными плоскостями V₁ и V₂ , проходящими через стороны угла АВС. Угол β для данного двугранного угла является линейным. Следовательно, углу β равен всякий другой линейный угол, вершина которого находится в любой точке на отвесном ребре ВВ₁ двугранного угла, а стороны его лежат в плоскости, параллельной плоскости М. Итак, для измерения величины угла abc = β можно в любой точке, лежащей на ребре ВВ₁ двугранного угла, допустим в точке b₁, установить горизонтальный круг с градусными делениями и измерить на нем дугу a₁c₁, заключенную между сторонами двугранного угла, которая и будет градусной мерой угла a₁b₁c₁, равной β , т.е. угол abc = β.

Как известно, теодолит является точным, по устройству тонким и чувствительным оптико-механическим прибором, с большим количествомтщательно подогнанных деталей. В связи с чем, качество и надежность результатов измерений, а также удобство эксплуатации и производительность работ, прямым образом зависит от умелого, бережного и внимательного обращения с прибором. Недостаточно бережная эксплуатация теодолита, зачастую, приводит к расстройству взаимного положения его частей, а нередко и к выходу прибора из строя. Поэтому работая с теодолитом, а также при его транспортировке и хранении, следует строго придерживаться следующих простых правил:

 

1.     Прежде всего, необходимо научиться правильно укладывать теодолит в транспортировочный кейс. Перед первым применением внимательно ознакомьтесь, как уложен теодолит в транспортировочном кейсе и запомните положение отдельных его частей.

При вынимании и укладке в транспортировочный кейс теодолит необходимо брать за специальную ручку или за подставку с подъемными винтами.

При укладке теодолита в транспортировочный кейс предварительно необходимо отжать закрепительные винты алидады и зрительной трубы. Когда теодолит займет надлежащие положение закрепительные винты трубы и алидады снова заворачивают. Крышка транспортировочного кейса должна легко закрываться, в обратном случае необходимо проверить правильность укладки теодолита.

 

2. Ножки штатива, перед его установкой, необходимо расслабить, отвернув зажимные винты(барашки) или открыв фиксирующие клипсы; далее необходимо зафиксировать ножки на необходимой высоте и вдавить их с достаточным усилием (усилие должно прилагаться вдоль оси ножек) в грунт, головка штатива при этом должна быть расположена горизонтально. На зыбком грунте штатив должен быть установлен на забитые деревянные колья.

 

3. Вынутый из транспортировочного кейса теодолит и установленный на штативе, он должен быть сразу же закреплен становым винтом. Нельзя оставлять теодолит на штативе незакрепленным даже на короткий промежуток времени.

 

4. Необходимо следить, чтобы подъемные и наводящие винты работали своей средней частью; не следует допускать ввинчивания или вывинчивания этих винтов до отказа.

 

2.     Точное наведение на цель следует заканчивать ввинчиванием, а не вывинчиванием наводящих винтов.

 

3.     Вращение подвижных частей теодолита (зрительной трубы и алидады), после открепления зажимных винтов, должно происходить легко, без усилий. В обратном случае, необходимо внимательно изучить и устранить причину туго, заедающего вращения.

 

4.     Переноска теодолита с одной точки на другую может быть произведена в транспортировочном кейсе или на штативе на плече вертикально.

 

8. При транспортировке теодолита на большие расстояния необходимо исключить возможность ударов, падений, толчков и тряски прибора. Для этого прибор в транспортировочном кейсе фиксируется на амортизирующих поверхностях.

 

9. Не допускается работа с теодолитом в дождливую погоду. При кратковременном дожде теодолит можно оставить на штативе, при этом прибор следует обязательно накрыть непромокаемым чехлом. По возвращении отсыревший теодолит необходимо незамедлительно вынуть из транспортировочного ящика и дать ему просохнуть, после чего протереть мягкой сухой тряпкой.

 

Эти простые, но в тоже время важные правила помогут избежать возможных проблем при эксплуатации теодолита, будь, то оптический или электронный.

 

 

 

 

 

 

 

 

 

 

 

 

·        УСТРОЙСТВО ТЕОДОЛИТА

Теодолит – это геодезический прибор, предназначенный для измерения горизонтальных и вертикальных углов. Происхождение слова «теодолит»,  связано с греческими словами theomai смотрю, вижу и dolichos – длинный, далеко.

Теодолиты различаются по точности, способу отсчитывания по лимбу, по конструкции, назначению и другим признакам.

По точности теодолиты делятся на:

- высокоточные, с помощью которых горизонтальный угол измеряется одним полным приемом со средней квадратической погрешностью от ± 0,5» до ± 1»;

- точные, позволяющие измерять горизонтальный угол одним приемом со средней квадратической погрешностью от ± 2» до ± 15»;

- технические – со средней квадратической погрешностью от ± 20» до ± 60».

 

Средняя квадратическая погрешность измерения горизонтального угла указывается в шифре теодолита цифрами, например, Т2, Т5, Т30. В случае применения зрительной трубы с прямым изображением в шифре теодолита добавляется буква П, например, 2Т30П – теодолит со средней квадратической погрешностью измерения горизонтального угла ± 30» и с трубой прямого изображения. Цифра 2 впереди шифра обозначает, что это теодолит второго поколения, то есть более совершенный, чем теодолит марки Т30.

Теодолит Т30 (рис.1) и его модификации (2Т30, 2Т30П) относятся к разряду технических, с повторительной системой вертикальной оси. Система отсчитывания односторонняя. Увеличение трубы 18х (Т30) и 20х (2Т30), пределы визирования от 1,2 м до бесконечности, цена деления цилиндрического уровня 45». Данные теодолиты применяются для прокладывания теодолитных и тахеометрических ходов, плановых и высотных съемок.

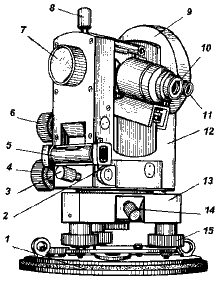
Рис.1. Теодолит Т30

1 – основание; 2 – исправительный винт цилиндрического уровня;

3, 4 – закрепительный и наводящий винты алидады; 5 – цилиндрический уровень; 6 – наводящий винт зрительной трубы; 7 – кремальера; 8 – закрепительный винт зрительной трубы; 9 – визир; 10 – окуляр зрительной трубы;   11 – окуляр отсчетного микроскопа;       12 – колонка;         13 – подставка;        14 – закрепительный винт лимба;  15 – подъемный винт

В теодолите Т30 отсчетное приспособление выполнено в виде штрихового микроскопа, позволяющего брать отсчеты с точностью 1', а в его модификациях (2Т30, 3Т30) – шкалового микроскопа тридцатисекундной точности.

На зрительной трубе имеется оптический визир 9 (рис.1), в поле зрения которого виден светлый крест. Этот крест совмещается с предметом, который должен попасть в поле зрения зрительной трубы, но изображение предмета может быть размытым (иногда его изображение вообще не будет видно). Для получения четкого изображения предмета необходимо с помощью кремальеры 7 перемещать в трубе специальную фокусирующую линзу до тех пор, пока его изображение не станет четким. Зажимные винты зрительной трубы 8 и алидады горизонтального круга 3 закрепляются, и микрометренными винтами алидады горизонтального круга 4 и зрительной трубы 6 центр сетки нитей наводится на предмет. Отчетливость изображения сетки нитей получают вращением диоптрийного кольца окуляра трубы 10.

В теодолите Т30 подставка 13 жестко скреплена с основанием 1, служащим одновременно донцем футляра, что позволяет закрывать теодолит футляром, не снимая его со штатива. Ось вращения теодолита устанавливается в отвесное положение с помощью подъемных винтов 15 и цилиндрического уровня при алидаде горизонтального круга 5.

Полая вертикальная ось теодолита позволяет центрировать прибор над точкой местности с помощью зрительной трубы. Прибор снабжается окулярными насадками для зрительной трубы и микроскопа, которые применяют при наблюдении предметов, расположенных относительно горизонта под углом более 45°  .

В теодолитах Т30 имеется только один цилиндрический уровень при алидаде горизонтального круга 5, который прикрепляется к подставке зрительной трубы параллельно визирной плоскости. Положение уровня изменяется юстировочными (исправительными) винтами 2. При алидаде вертикального круга уровня нет.

Теодолит может быть укомплектован ориентир-буссолью и уровнем, который прикрепляется к трубе для нивелирования горизонтальным визирным лучом. Обычно к зрительной трубе прикрепляют два визира. При установке уровня на трубе один из визиров должен быть снят.

 

·        КОНСТРУКТИВНЫЕ ЭЛЕМЕНТЫ ГЕОДЕЗИЧЕСКИХ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ

·        ОТСЧЕТНЫЕ ПРИСПОСОБЛЕНИЯ

 

Приспособление, несущее единицу измерения, называется рабочей мерой. Отсчитывание по шкале рабочей меры производят по отсчетному индексу (начало и конец отрезка линии, сторона угла, штрих логарифмической линейки, стрелка весов и т.п.). В общем случае отсчетный индекс (на рис.2. – О.И.) устанавливается между двумя штрихами шкалы; один из них называют младшим штрихом (мл.), другой – старшим (ст.).

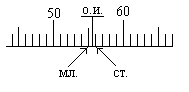
Рис.2 Установка отсчетного индекса

 

Отсчет N по шкале равен сумме двух величин:

N = Nмл + x, где Nмл – значение младшего штриха шкалы, Nмл = 55,
x – доля цены деления шкалы от младшего штриха до отсчетного индекса, x = 0,6

·        ШТРИХОВОЙ МИКРОСКОП.

 Отсчетным индексом в штриховом микроскопе является неподвижный штрих, выгравированный на стеклянной пластинке, помещенной на пути хода лучей, идущих от осветитель ного окошка через штрихи лимба в отсчетный микроскоп. Оценка доли деления лимба выполняется на глаз. Из опыта установлено, что при отсчитывании на глаз наибольшая точность достигается при видимом расстоянии между штрихами 2.00 мм и толщине штрихов 0.10 мм; при таких условиях ошибка отсчета составляет 0.1 деления.

В поле зрения окуляра штрихового микроскопа видны деления лимба и отсчетный индекс – штрих; отсчет по горизонтальному кругу (Г) равен 69^o47', по вертикальному (В) – 358^o150' (рис.3).

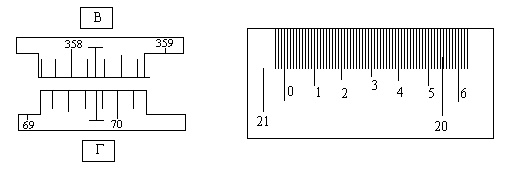
Рис.3                                                       Рис.4

 

·        ШКАЛОВОЙ МИКРОСКОП.

 

На пути хода лучей от осветительного окошка через штрихи лимба в поле зрения микроскопа помещена стеклянная пластинка с гравированной шкалой. Длина шкалы равна длине одного деления лимба λ; шкала разделена на n равных частей, цена одного деления шкалы шкалового микроскопа обозначается буквой μ и равна  μ = λ / n .

Отсчетным индексом является нулевой штрих шкалы шкалового микроскопа. Доля деления лимба от младшего штриха шкалы лимба до отсчетного индекса измеряется непосредственно по шкале микроскопа, так как направления возрастания делений на лимбе и на шкале микроскопа противоположные (рис.4). Доля деления шкалы микроскопа оценивается на глаз. Полный отсчет по лимбу равен сумме отсчетов по младшему штриху лимба Nмл и по шкале микроскопа Nш:

N = Nмл + Nш,

на рис. 4 отсчет по лимбу (λ=1^o, n=60, μ=1' ) равен N = 20^o + 54.3' = 20^o 54.3'.

 

·        ПОЛЕ ЗРЕНИЯ ТРУБЫ.

Полем зрения трубы называют участок пространства, видимый в трубу при неподвижном ее положении. Поле зрения измеряют углом ε, вершина которого лежит в оптическом центре объектива, а стороны касаются краев отверстия диафрагмы (рис.5)

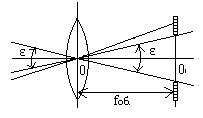
Рис. 5

Обычно в геодезических приборах принимают d1 = 0.7 * fок, тогда в радианной мере ε = 0.7 / V.  Если ε выразить в градусах, то:  ε = 40o / V .

Чем больше увеличение трубы, тем меньше ее угол зрения. Так, например, при V = 20x ε = 2o, а при V = 80x ε = 0.5o.

 

·        ПРАВИЛА ЭКСПЛУАТАЦИИ И ОБРАЩЕНИЯ С ТЕОДОЛИТОМ

Теодолит является сложным и чувствительным оптико-механическим прибором. Данный прибор требует умелого и внимательного обращения во время работы, проведения своевременных регламентных работ, тщательного ухода. Обращаться с теодолитом следует с особой аккуратностью.

Перед использованием теодолита для наблюдений необходимо проверить общее состояние прибора, состояние оптических поверхностей и ампул уровней, наличие указанных в паспорте принадлежностей в комплекте. Далее проверяют вращение алидады и зрительной трубы, работу переключателя отсчетной системы, зажимных и отсчетных устройств, окуляров, кремальеры, плавность вращения подъемных винтов.

Разборка и чистка внутренних частей теодолита требует определенных навыков, наблюдатель же может выполнить несложные операции, особенно осторожно следует выполнять чистку просветленной оптики теодолита, которая особенно чувствительна к механическим повреждениям.

Во время производства наблюдений прибор рекомендуется защищать от нагрева солнцем и непосредственного воздействия осадков. Если теодолит попал под дождь, его необходимо обсушить и протереть мягкой салфеткой, не допуская сушку теодолита вблизи источников тепла.

При внесении теодолита с холода в теплое помещение футляр необходимо оставить закрытым в течение часа, а потом постепенно приоткрывать, обеспечивая плавный переход от холода к теплу. Перевозить и переносить теодолит нужно только в вертикальном положении, предварительно убедившись в надежном закреплении прибора в упаковке.

 

·        ПРАВИЛА УСТАНОВКИ ТЕОДОЛИТА В РАБОЧЕЕ ПОЛОЖЕНИЕ

Для приведения теодолита в рабочее положение (после установки на штатив) следует выполнить следующие действия:

-Центрирование теодолита над точкой, являющейся вершиной измеряемого угла

-Нивелирование прибора

 

Центрирование осуществляется с помощью нитяного или оптического отвеса путем совмещения острия отвеса с центром пункта (крест или шляпка гвоздя на колышке). Штатив устанавливают с таким расчетом, чтобы центр оверстия головки находился примерно по вертикали, проходящей через точку. Необходимые перемещения штатива осуществляют вдавливанием его ножек в грунт или изменением длины ножек.

Отклонение острия отвеса от центра пункта  не должно превышать  1-3 мм.

Нивелирование заключается в приведение вертикальной (основной) оси теодолита в отвесное положение. Для этого:

1.     цилиндрический уровень горизонтального круга устанавливают параллельно линии, соединяющей два подъемных винта и вращая их  приводят пузырек уровня в середину ампулы (нульпункт)

2.     после этого поворачивают  алидаду на 90^o, и  устанавливают уровень по направлению третьего подъемного винта, и, действуя этим винтом, приводят пузырек уровня в нульпункт.

3.     После этого вращают алидаду и устанавливают ее в произвольное положение; пузырек уровня должен оставаться в нульпункте.

Если пузырек уровня отклоняется от нульпункта больше, чем на одно деление, следует заново выполнить шаги 1-3 и снова установить ось вращения алидады в вертикальное положение.

Процедура установки оси вращения алидады в вертикальное положение называется горизонтированием теодолита.

 

·        ПОВЕРКИ ТЕОДОЛИТА, ПОРЯДОК ВЫПОЛНЕНИЯ, ДОПУСКИ И ЮСТИРОВКА.

Чтобы теодолит обеспечивал получение неискаженных результатов измерений, он должен удовлетворять соответствующим геометрическим и оптико-механическим условиям. Действия, связанные с проверкой этих условий, называют поверками. Если какое-либо условие не соблюдается, производят его исправление, т.е. юстировку.

Оптико-механические условия:

-         зрительные трубы, лупы и микроскопы должны иметь надлежащее увеличение и достаточное поле зрение, обеспечивать четкие изображения предметов наблюдения и отсчетных шкал;

-         подвижные части теодолита должны правильно и плавно перемещаться в соответствующих плоскостях.

 

Геометрические условия (рис.6):

1.     ось цилиндрического уровня при алидаде горизонтального круга PQ должна быть перпендикулярна к вертикальной оси вращения теодолита MN;

2.     визирная ось зрительной трубы CD должна быть перпендикулярна к горизонтальной оси ее вращения AB;

3.     ось вращения зрительной трубы AB должна быть перпендикулярна к оси вращения теодолита MN.

 

Нарушение этих условий приводит к появлению систематических погрешностей при измерении углов. Для того, чтобы исключить влияние этих погрешностей на результаты наблюдений, теодолит подвергается  специальным поверкам. Все поверки имеют свой номер и выполняются в строгой последовательности, соответствующей их нумерации

 

рис. 6

1.1.     Поверка цилиндрического уровня

Ось цилиндрического уровня алидады горизонтального круга должна быть перпендикулярна к оси вращения теодолита (ZZ).

Выполнение этого условия позволяет с помощью уровня устанавливать ось вращения теодолита в отвесное положение, а плоскость лимба – в горизонтально положение.

Порядок действий:

1.     Закрепляют теодолит на штативе и производят приближенное горизонтирование прибора по уровню.

2.     Устанавливают поверяемый уровень по направлению двух подъемных винтов и вращением их в разные стороны выводят пузырек уровня в нуль-пункт (рис.2.1, а).

3.     Поворачивают алидаду на 180 градусов. Если после поворота пузырек уровня остаётся в нуль-пункте, то условие перпендикулярности осей UU и ZZ выполняется.

4.     В случае смещения пузырька производят исправление положения уровня. Для этого с помощью юстировочного винта уровня перемещают пузырек по направлению к нуль-пункту на половину дуги отклонения (см.рис.2.1,б).

После юстировки уровня следует повторить поверку и убедиться в выполнении требуемого условия. Практически условие считается выполненным, если после поворота на 180 градусов пузырек уровня отклоняется от нуль-пункта в пределах одного деления шкалы ампулы.

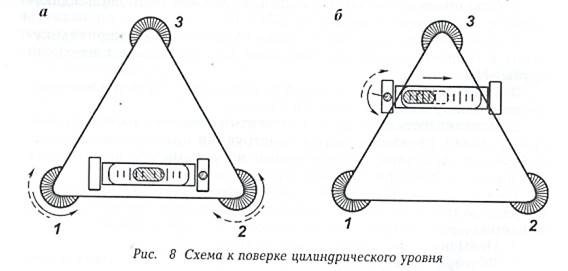
Рисунок  1.1

1.2.     Поверка положения коллимационной плоскости

Визирная ось зрительной трубы должна быть перпендикулярна к горизонтальной оси (оси вращения трубы) теодолита (VVHH).

Если указанное условие выполняется, то при вращении зрительной трубы вокруг горизонтальной оси HH визирная ось образует коллимационную плоскость. При невыполнении условия визирная ось будет описывать не плоскость, а две конические поверхности.

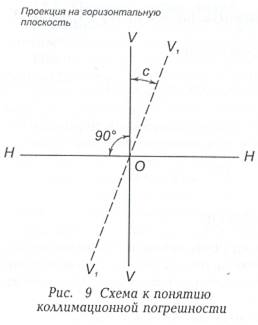Рисунок  2.2

 

Угол между фактическим положением визирной оси  и плоскостью, перпендикулярной к горизонтальной оси теодолита HH (рис.2.2) называется коллимационной погрешностью.

Порядок действий:

1.     Теодолит устанавливают в рабочее положение; на местности выбирают ясно видимый удаленный (на несколько сотен метров) предмет, расположенный примерно на горизонте прибора. Визируют на цель при первом положении вертикального круга (КЛ) и берут отсчет по горизонтальному кругу .

2.     Переводят трубу через зенит и, вращая алидаду, визируют на цель при втором положении вертикального круга (КП) и берут отсчет по горизонтальному кругу .

3.     Вычисляют коллимационную погрешность:

 

с = .

 

Поверяемое условие считается выполненным, если коллимационная погрешность не превышает двойной точности отсчетного устройства (с. В противном случае (с производят исправление положения визирной оси.

4.     Вычисляют правильный отсчет М, свободный от влияния коллимационной погрешности:

М =

или

М =  – с.

5.     Вычисленный отсчет М наводящим винтом алидады горизонтального круга устанавливают на лимбе. При этом ’алидада повернется на угол с, а перекрестие сетки нитей отклонится от изображения наблюдаемой цели. Тогда, ослабив вертикальные винты оправы сетки нитей, с помощью боковых юстировочных винтов перемещают сетку нитей до совмещения ее перекрестия с визирной целью. После этого сетку закрепляют вертикальными винтами и вновь повторяют поверку.

6.     Следует помнить, что среднее из отсчетов по горизонтальному кругу, взятых при двух положениях вертикального круга (КЛ и КП), свободно от влияния коллимационной погрешности.

Пример: при КЛ отсчет по горизонтальному кругу  = 70’; при КП  = 187’.

Величина коллимационной погрешности:

С =  = -3,0, т.е. с .

Правильный отсчет, т.е. отсчет, соответствующий перпендикулярному положению визирной оси к оси вращения трубы будет

М = =187

Или М = 187- (-3,0) = 18734,0.

Наблюдая в отсчетный микроскоп, устанавливают этот отсчет на лимбе горизонтального круга. Действуя боковыми юстировочными винтами сетки, совмещают ее перекрестие с визирной целью.

1.3.     Поверка положения горизонтальной оси теодолита

Горизонтальная ось теодолита должна быть перпендикулярна к оси вращения теодолита (HHZZ).

Выполнение условия необходимо для того, чтобы после горизонтирования теодолита коллимационная плоскость занимала отвесное положение.

Порядок действий:

1.     Теодолит устанавливают в 10-20 м от стены здания. Зрительную трубу наводят на высоко расположенную точку А на стене здания (рис.2.3).

Рисунок  3.3

 

2.     Наклоняя трубу, проектируют эту точку до горизонтального положения визирной оси и отмечают на прилепленном к стене листе бумаги проекцию точки.

3.     Переводят трубу через зенит и, повторив ту же операцию при втором положении трубы, отмечают проекцию точки а₂.

4.    Если отношение отрезков, то условие считается выполненным. В случае несоблюдения условия исправление положения горизонтальной оси теодолита допускается только в оптико-механической мастерской, так как оно требует частичной разборки прибора.

Следует учесть, что среднее из отсчетов по лимбу, взятых при визировании на точку при двух положениях трубы (КЛ и КП), свободно от влияния наклона оси вращения трубы.

1.4.     Поверка сетки нитей

Вертикальный штрих сетки нитей должен располагаться в коллимационной плоскости трубы.

Иначе, горизонтальный штрих сетки нитей должен быть перпендикулярным к оси вращения теодолита ZZ.

Выполнение данного условия требуется для создания удобств при визировании на отвесные предметы (например, вехи).

Порядок действий:

1.     Тщательно установив ось вращения теодолита в отвесное положение, визируют на нить отвеса, подвешенного на расстоянии 5-10 м от прибора.

2.   Если вертикальный штрих сетки отклоняется от отвесной линии более чем на  величины биссектора сетки нитей, то необходимо исправить положение сетки нитей путем ее поворота. Для этого слегка ослабляют винты, скрепляющие окулярную часть с корпусом трубы, и поворачивают окулярную часть вместе с сеткой нитей до требуемого положения; затем винты закрепляют.

3.     После юстировки второй основной штрих сетки нитей должен быть  горизонтальным, так как взаимная перпендикулярность штрихов гарантируется заводом-изготовителем. Чтобы убедиться в этом, наводят горизонтальный штрих на хорошо видимую точку и наводящим винтом поворачивают алидаду горизонтального круга; при этом поверяемый штрих должен оставаться на изображении точки.

После производства данной поверки и юстировки необходимо повторить поверку положения коллимационной плоскости.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМА 6: ГЕОМЕТРИЧЕСКОЕ НИВЕЛИРОВАНИЕ

Нивелирование – один из видов полевых геодезических измерений для определения превышений (разности отметок) между точками. С помощью нивелира и нивелирных реек выполняется геометрическое нивелирование. Геометрическое нивелирование заключается в непосредственном определении разности высот двух точек с помощью горизонтального визирного луча, получаемого прибором – нивелиром.

      Нивелиром выполняют различные геодезические работы: нивелирование трассы, нивелирование поверхности, передачу отметок на монтажные горизонты, проверку горизонтальности перекрытий и др.

Нивелирование – процесс геодезических измерений для определения превышения точек одной над другой и высот точек над уровнем моря.

Назначение нивелирования – для определения высот точек при топографической съемке, составлении карт, планов, профилей, для установки строительных конструкций, для наблюдения за осадкой и деформациями зданий, для строительства линейных сооружений, установки ускорителей на АЭС. В России принята Балтийская система высот.

Кроншта́дтский футшто́к — футшток для измерения высоты уровня Балтийского моря. Медная пластина, укреплённая на устое Синего моста через Обводный канал в Кронштадте. Средний многолетний уровень моря (по наблюдениям с 1825 по 1840 г.) – принят за нулевую отметку.

Счет абсолютных высот ведут от уровенной поверхности, проходящей через нуль Кронштадтского футштока. Если счет высот ведется от другой поверхности, такая высота называется относительной высотой.

 

 

·        МЕТОДЫ НИВЕЛИРОВАНИЯ

 Различают следующие виды: геометрическое, тригонометрическое, гидростатическое, барометрическое, механическое, стереофотограмметрическое.

Геометрическое нивелирование производится горизонтальным визирным лучом, который получают чаще всего при помощи приборов, называемых нивелирами. Точность геометрического нивелирования характеризуется средней квадратической  погрешностью нивелирования на 1 км двойного хода равной от 0.5 до 10.0 мм в зависимости от типа используемых приборов.

Тригонометрическое нивелирование предусматривает измерение расстояния и угла наклона, которые необходимы для вычисления превышения по тригонометрическим формулам. Точность определения превышения на станции зависит от погрешностей измерений угла и расстояния и обычно на один порядок (в 10 раз) меньше чем при геометрическом нивелировании.

Гидростатическое нивелирование основано на свойстве поверхности жидкости в сообщающихся сосудах устанавливаться на одной высоте. Этот метод применяют для выверки строительных конструкций по высоте в стесненных условиях, а также при наблюдениях за деформациями инженерных сооружений. Точность определения превышений достигает 0.1 – 1.0 мм.

Барометрическое нивелирование использует зависимость высот точек местности от величины атмосферного давления в этих точках. Наиболее точные барометры позволяют определять превышения с погрешностью 0.3 -0.5 м.

Радиолокационное нивелирование  производят с летательных аппаратов посредством определения длины пути прохождения электромагнитных волн отраженных от земной поверхности.

Механическое нивелирование производят при помощи специального прибора, содержащего датчик углов наклона продольной оси транспортного средства относительно маятника, сохраняющего отвесное положение, и датчик пути. Погрешность такого нивелирования со скоростью 30 км/ч от 0.3 до 0.6 м на 1 км хода.

Репер – постоянный знак закрепления нивелирного хода.

Пользуясь репером и нивелиром, можно установить в натуре положение любой точки по высоте.

Реперы прочно закреплены в грунте или на цоколе капитальных зданий.

 

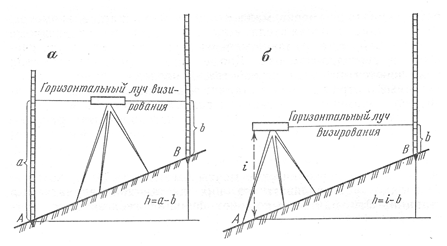
 а – способ нивелирования «из середины»;

б – способ нивелирования «вперед»

 

 

·        ГЕОМЕТРИЧЕСКОЕ НИВЕЛИРОВАНИЕ

Основано на горизонтальном луче визирования, создаваемом нивелиром с помощью цилиндрического уровня.

Высоту точек местности определяют измерением превышений h между ними. Зная высоту Н_А начальной точки А над уровнем моря или какой-либо другой уровенной поверхностью MN, высоту Н_В определяемой точки В находят по формуле:

H_B = H_A + h.

 

·        НИВЕЛИРОВАНИЕ ВПЕРЕД

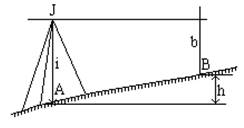
1.     При нивелировании вперед нивелир устанавливают над точкой А так, чтобы окуляр трубы был на одной отвесной линии с точкой.

2.     На точку В ставят рейку.

3.      Измеряют высоту нивелира i над точкой А и берут отсчет b по рейке.

4.     Превышение h подсчитывают по формуле:h = i –b.

5.     Отметку точки B можно вычислить через превышение по формуле или через горизонт прибора: H _в = H _г – b.

 

 

 

 

·        НИВЕЛИРОВАНИЕ ИЗ СЕРЕДИНЫ

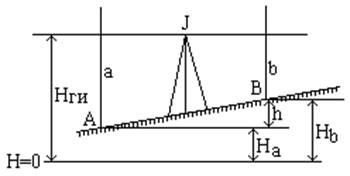
Нивелир устанавливают посредине между точками А и В, а на точках А и В ставят рейки с делениями. При движении от точки A к точке B рейка в точке А называется задней ( З), рейка в точке В – передней ( П ).

5.     Сначала наводят трубу на заднюю рейку и берут отсчет a,

6.     Затем наводят трубу на переднюю рейку и берут отсчет b.

7.     Превышение точки b относительно точки а получают по формуле

h = a – b, или (h = З – П)

8.     Если a > b, превышение положительное, если a < b –отрицательное.

9.     Отметка точки В вычисляется по формуле: H_в = H_а + h.

10. Высота визирного луча над уровнем моря называется горизонтом прибора и обозначается H _г:          H _г = H_А + a = H_В + b.

 

 

 

 

 

 

 

·        ЖУРНАЛ ТЕХНИЧЕСКОГО НИВЕЛИРОВАНИЯ

№№ст.	№№т	Отсчеты по рейке			Превышения		Ср.превыш.		Г.И.	Отметки    точек
		Задн.	Перед.	Пром.	+	--	+	--
1	А   В	1218 5900	1447 6131			229 231		230		33.456   33.226

 

h = З-П = 1218-1447 = -229 мм

h = З-П = 5900-6131 = -231 мм

h _СР = -230 мм

ГИ = H_А + a, (м)

H = H_А – h _СР

 

 

 

 

 

 

 

·        СЛОЖНОЕ НИВЕЛИРОВАНИЕ

Если точки А и В находятся на большом расстоянии одна от другой и превышение между ними нельзя измерить с одной установки нивелира, то на линии AB намечают промежуточные точки 1, 2, 3 и т.д. и измеряют превышение по частям

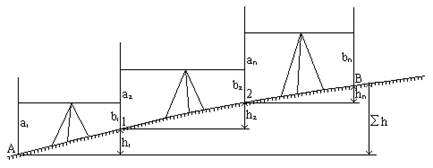
Точки, позволяющие связать горизонты прибора на соседних установках нивелира, называются связующими; на этих точках отсчеты берут два раза – сначала по передней рейке, а затем по задней.

При последовательном нивелировании получается нивелирный ход.

         Вращением элевационного винта точно совмещают изображения концов пузырька в поле зрения трубы, приводя уровень «в контакт».

         В этот момент, пользуясь средней горизонтальной нитью, снимают отсчет по рейке. Дециметры считывают по надписям на рейке, сантиметры определяют по числу делений рейки, а миллиметры оценивают на глаз. На рисунке показан отсчет по рейке 1250мм.

 

 

 

 

 

·        КЛАССИФИКАЦИЯ НИВЕЛИРОВ

    Нивелиры классифицируются по точности и по конструкции. По точности нивелиры выпускают:

- высокоточные – нивелир Н-05 имеет погрешность не более 0.5мм на 1км хода;

- точные – нивелиры Н-3, Н-3Л, Н-3К, Н-3КЛ – дают погрешность не более 3мм на 1км хода;

-технические – нивелиры Н-5, Н-10, Н-10КЛ – не более 10мм на 1км хода.

    По конструкции нивелиры всех типов выпускаются в двух исполнениях: с цилиндрическим уровнем и с компенсатором. Если нивелир с компенсатором, к названию прибора добавляется буква «К», например, Н-3К.

    Часть моделей нивелиров выпускается с лимбом для измерения горизонтальных углов; в этом случае к названию прибора добавляется буква «Л», например, Н-3КЛ.

    Выпускались нивелиры 2,3 и 4-ого поколений. Цифра, стоящая перед обозначением марки прибора, указывает номер улучшенной модификации базовой модели, например, 4Н-5Л. Нивелиры 2, 3, 4 поколений имеют зрительную трубу прямого изображения.

    Все перечисленные выше нивелиры относятся к оптическим приборам. В настоящее время выпускаются и находят широкое применение лазерные и цифровые (электронные) нивелиры. Тем не менее, наиболее широко используется на строительной площадке нивелир базовой модели Н-3, поэтому в дальнейшем рассмотрим его устройство и работу с ним.  

 

 

·        УСТРОЙСТВО НИВЕЛИРА

 

 

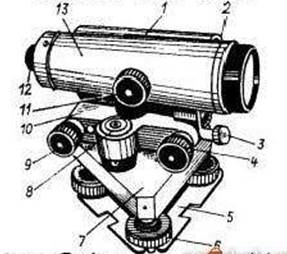
1 – Корпус цилиндрического уровня

2 – Мушка и визир для грубой наводки

3 – Закрепительный винт зрительной трубы

4 – Наводящий – микрометренный винт

5 – Пружинящая пластина

6 – Подъёмный вит

7 – Подставка – трегер

8 – Круглый уровень

9 – Элевационный винт

10 –Подставка

11 –Винт фокусировки трубы

12 –Юстировочные винты круглого уровня

13 – Зрительная труба

·        НИВЕЛИРЫ С ЦИЛИНДРИЧЕСКИМИ УРОВНЯМИ

      Рассмотрим устройство нивелиров с цилиндрическими уровнями на примере нивелира Н-3 (рис 1,а).

 

4

                                                                                           4                                         

                                                                                                                             4 

 

 

 

 

 

                                                                                                  

                      а)                               Рис.1                                  б)

                                а) – основные части нивелира Н-3;

                                б)- поле зрения зрительной трубы нивелира Н-3

 

     Н-3 – точный нивелир с цилиндрическим уровнем и элевационным винтом. Верхняя вращающаяся часть состоит из зрительной трубы (1), жестко скрепленного с трубой цилиндрического уровня, круглого уровня (5), закрепительного (3) и наводящего (4) винтов  трубы и элевационного винта (6).

     Нижняя часть состоит из подставки с тремя подъемными винтами (трегер) и прижимной пластины. Прибор приводится в рабочее положение вращением подъемных винтов трегера по круглому уровню.

     Зрительная труба представляет собой телескопическую систему, состоящую из объектива, фокусирующей линзы (кремальера), сетки нитей и окуляра. Изображение концов пузырька цилиндрического уровня с

помощью системы призм передается в поле зрения зрительной трубы (рис.1,б). Пузырек цилиндрического уровня приводится на середину элевационным винтом (6). Резкость изображения нивелирной рейки достигается вращением винта (2) фокусирующей линзы. Затем снимается отсчет по рейке (на рис. 1, а, отсчет 1250).                                                                                                                       

·        НИВЕЛИРЫ С КОМПЕНСАТОРАМИ

      Нивелиры с компенсаторами углов наклона называются самоустанавливающимися. Компенсация углов наклона визирной оси или автоматическое приведение ее в горизонтальное положение у таких нивелиров происходит за счет автоматического поворота компенсатора    

оптической  системы.   У нивелира Н-3К, например, диапазон   работы

компенсатора 16'. Устанавливают нивелир в рабочее положение подъем-

ными винтами по круглому уровню. Затем  наводят трубу на рейку

вначале от руки, затем наводящим винтом и снимают отсчет по рейке.                                                                                                                                                                                                                                                                                                                                                         

     Основные технические характеристики рассмотренных нивелиров приведены в табл. 1.

 

 

 

Техническая характеристика приборов.                                        Таблица 1 

Технические характеристики	Н-3	Н-3К
Увеличение зрительной трубы                               31.5х                 30х Коэффициент нитяного дальномера                       100                  100 Наименьшее расстояние визированием, м             1.0                   2.0 Цена деления круглого уровня, угловая                 10                    10 минута Цена деления цилиндрического уровня,                 15                     - угловая секунда Диапазон работ компенсатора, угловая                    -                     ±16 минута Масса нивелира, кг                                                    2.0                   1.8

 

 

 

 

 

 

 

 

 

·        НИВЕЛИРНЫЕ РЕЙКИ

            Нивелирные рейки изготавливаются из деревянного бруска двутаврового сечения толщиной 2-3 см, длиной 4м, 3м, 1.5м. 1.2м и короче, складные и цельные (рис.2,а). Основная шкала (черная сторона) состоит из чередующихся черных и белых сантиметровых делений. Счет делений ведут от нуля, совмещенного с основанием рейки, называемого «пяткой». На дополнительной шкале (красная сторона) начальный отсчет выражается определенным числом. Разность отсчетов по основной и дополнительной шкалам рейки должна оставаться всегда постоянной, что служит контролем правильности снятия отсчетов по рейке на станции.

            В комплект нивелира с прямой трубой входят рейки с прямыми надписями.

           Для удобства и  быстроты установки нивелирные рейки иногда снабжают круглыми уровнями. Рейки маркируют так: например, РН-10П-3000С, что означает, что эта рейка нивелирная, со шкалой деления 10мм, прямой надписью цифр, длиной 3000мм, складная.

          При производстве нивелирования I и II классов используются штриховые инварные рейки (рис.2,б).

           Во время работы рейки ставят на башмаки (рис.2.г), костыли (рис.2,в)

 или  деревянные колья.      

При работе с нивелирами применяются нивелирные рейки трех типов: РН-0,5 (для высокоточного нивелирования), РН-3 (для точного нивелирования) и РН-10 (для технического нивелирования). Назначение реек – фиксировать вертикальные расстояния от нивелируемых точек до горизонтального визирного луча (путем взятия так называемых отсчётов по рейкам).

                                                                                                                     

 

 

 

 

 

 

 

 

Рис.2

                               а – рейка РН-10;

                               б – инварная рейка РН-05 в поле зрения трубы;

                               в – костыль;

                               г – башмак

 

 

 

 

 

 

 

·        ПОВЕРКИ И ЮСТИРОВКИ НИВЕЛИРА

       При подготовке  нивелира к работе  выполняют следующие поверки:

 1. Поверка правильности установки круглого уровня;

2. Поверка правильности установки сетки нити;

3. Поверка нивелира на главное условие.

 

 

 

 

 

 

 

 

 

 

                             Рис.4.Поверки нивелира:

                        а,б,в—схема расположения осей;

                        г- положение нивелира при поверке главного условия;

                        д- положения пузырька круглого уровня.

 

 

1-ая поверка. Поверка правильности установки круглого уровня

Условие поверки: ось круглого уровня UU должна быть параллельна оси вращения JJ нивелира (рис. 4,а  и 4,д).

       Вращением трех подъемных винтов трегера пузырек круглого уровня приводят на середину. Затем верхнюю часть нивелира поворачивают на

180^о. Если при этом пузырек остается в центре, то поверка выполнена. При смещении пузырька более, чем на 1.5 деления, выполняют юстировку: действуя исправительными винтами уровня смещают пузырек в сторону нуль – пункта на половину отклонения. На вторую половину отклонения пузырек смещается подъемными винтами.

 2-ая поверка. Поверка правильности установки сетки нити

Условие поверки: горизонтальная нить сетки АА должна быть перпендикулярна оси вращения JJ нивелира(рис.4,б).

              Наводят трубу нивелира на рейку на расстоянии 20-30м левым концом средней горизонтальной нити и снимают отсчет по рейке. Немного

повернув трубу, наводят на рейку правый конец средней горизонтальной

нити и снимают отсчет по рейке. Если отсчеты различаются, требуется юстировка сетки нитей. Для этого ослабляют закрепительные винты окуляра к зрительной трубе и поворачивают окуляр с сеткой нитей в нужную сторону.

3-тья поверка. Поверка нивелира на главное условие.

Условие поверки:   визирная ось VV зрительной трубы должна быть параллельна оси цилиндрического уровня  UU (для нивелиров с цилиндрическим уровнями рис.4,в).

      Поверка производится двойным нивелированием линии длиной 50-75м – способом «из середины» и способом «вперед». На концах линии АВ на колья устанавливают рейки. Установив нивелир на равных расстояниях от реек, берут отсчеты α₁ по задней и  b₁ по передней рейкам. Эти отсчеты   α₁  и b₁ отличают от правильных  α₁^пр  и     b₁^пр на одну и ту же ошибку Δ₁ (рис.4,г). Превышение  подсчитывается:

h₁₌α₁ – b₁ = (α₁^пр + Δ₁) – (b₁^пр + Δ₁) = α₁^пр – b₁^пр.

Превышение, найденное способом из середины получается правильным, т.к. ошибка Δ₁ исключается.

       Затем эти же точки нивелируются способом «вперед», когда нивелир устанавливается за задней рейкой на расстоянии 2-3 метра (рис. 4,г). Берутся отсчеты по ближней точке b₂ и дальней рейке а₂. Отсчет b₂ практически безошибочный из-за малости расстояния от нивелира до рейки, т.е. b ₂ =  b ₂^пр; отсчет а₂ содержит ошибку x, т.е. а₂= а₂^пр + x .

     Превышение

h₂ =  α₂ – b₂ = (α₂^пр + х) – b₂^пр = (α₂^пр – b₂^пр) + x.

 

Можно считать, что h₁=  α₁^пр – b₁^пр = α₂^пр – b₂^пр, потому

 

h₂= (α₂^пр – b₂^пр ) + x = h₁  +  x.

       Сравниваем превышения, найденные способом «из середины» и способом «вперед»

h₁ –  h₂ = x.

 

     Если | x | ≤ 4мм, то главное геометрическое условие выполняется.

     Если это условие не выполняется, то требуется юстировка.

     Для выполнения юстировки предвычисляют правильный отсчет на дальнюю рейку 

а₂^пр = а₂ – x.

 

             Вращением элевационного винта устанавливают среднюю  горизонтальную нить на этот предвычисленный отсчет а₂^пр, при этом пузырек цилиндрического уровня сойдет с нуль-пункта. Ослабив боковые

исправительные винты цилиндрического уровня, вертикальными исправительными винтами добиваются «контакта» изображений концов пузырька уровня.

      Для нивелиров с компенсатором (Н-3К, Н-10КЛ и т.д.) поверка главного условия  выполняется так же, а юстировка производится вращением исправительных винтов сетки нитей путем ее перемещения вверх или вниз.

     Нивелир с компенсатором не должен иметь недокомпенсации . Приведя нивелир в рабочее положение по круглому уровню и взяв отсчет по рейке, установленной в 40-50м, поворачивают один из подъемных винтов, расположенном в направлении рейки. Если в течение 1-2с первоначальный отсчет восстановится, это свидетельствует о нормальной работе компенсатора. В случае невыполнения условия, его необходимо сдать в мастерскую по ремонту геодезических приборов.

 

 

 

 

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что измеряет нивелир?

2. Для чего служит цилиндрический уровень при зрительной трубе нивелира?

3. Для чего применяется в нивелире компенсатор?

4. Как устроены рейки?

5. Как производится поверка круглого уровня?

6. Какое главное условие предъявляется к нивелиру?

7. Порядок производства поверки главного условия нивелира Н-3?

8. Последовательность снятия отсчетов по рейкам на станции технического нивелирования?

9. Как вычисляется превышение?

10. В чем заключается контроль правильности измерения на станции технического нивелирования?

 

 

 

 

 

 

ТЕМА 7: ГЕОДЕЗИЧЕСКИЕ СЪЕМКИ. ТЕОДОЛИТНЫЙ ХОД.

ПОЛЕВЫЕ И КАМЕРАЛЬНЫЕ РАБОТЫ. ПОНЯТИЕ О ТАХЕОМЕТРИЧЕСКОЙ СЪЕМКЕ

·        СУЩНОСТЬ ТЕОДОЛИТНОЙ СЪЁМКИ

Теодолитной называется горизонтальная (контурная) съёмка местности, в результате которой может быть получен план с изображением ситуации местности (контуров и местных предметов) без рельефа. Теодолитная съемка относится к числу крупномасштабных (масштаба 1:5000 и крупнее) и применяется в равнинной местности в условиях сложной ситуации и на застроенных территориях: в населенных пунктах, на строительных площадках, площадках горных предприятий, на территории железнодорожных узлов аэропортов и т.п. В качестве планового съемочного обоснования при теодолитной съемке обычно используются точки теодолитных ходов.

Теодолитные ходы представляют собой системы ломаных линий, в которых горизонтальные углы измеряются техническими теодолитами. А длины сторон – стальными мерными лентами и рулетками либо оптическими дальномерами. По точности теодолитные ходы подразделяются на разряды: ходы 1 разряда – с относительной погрешностью не ниже 1:2000, 2 разряда – не ниже 1:1000. Обычно теодолитные ходы нужны не только для выполнения съемки ситуации местности, но и служат геодезической основой для других видов инженерно-геодезических работ. Теодолитные ходы развиваются от пунктов плановых государственных геодезических сетей и сетей сгущения.

 

 

 

По форме различают следующие виды теодолитных ходов :

1)разомкнутый ход, начало и конец которого опираются на пункты геодезического обоснования (рис.1,а) ;

2)замкнутый ход (полигон) – сомкнутый многоугольник, обычно примыкающий к пункту геодезического обоснования (рис.1,б) ; 3)висячий ход, один из концов которого примыкает к пункту геодезического обоснования, а второй конец остаётся свободным (рис.1,в).

Рис. 1- Теодолитные ходы

 

При съемках населенных пунктов, строительных площадок, промплощадок предприятий и других обычно по границе участка прокладывают замкнутый полигон. При необходимости внутри полигона прокладывают диагональные ходы, которые могут образовывать узловые точки. Проложение висячих теодолитных ходов допускается лишь в отдельных случаях при съемке неответственных объектов; при этом длина висячего хода не должна превышать 300 м при съемках масштаба 1:2000 и 200 м – масштаба 1:1000.

Теодолитная съемка слагается из подготовительных, полевых и камеральных работ. Наибольший объем приходится на полевые работы, которые включают в себя рекогносцировку снимаемого участка, прокладку теодолитных ходов и полигонов, их привязку к пунктам геодезической опорной сети и съёмку ситуации.

 

·        ЭТАПЫ ТЕОДОЛИТНОЙ СЪЁМКИ

-         Подготовительные работы

-         Полевые работы

-         Рекогносцировка местности и закрепление точек теодолитных ходов

-         Прокладка теодолитных ходов на местности

-         Привязка теодолитных ходов к пунктам геодезической опорной сети

-         Съёмка ситуации местности

-         Камеральные работы при теодолитной съёмке

 

Камеральную обработку начинают с проверки и обработки полевых журналов. Затем составляют схему теодолитных ходов. У вершин подписывают средние значения горизонтальных углов, а возле каждой стороны – ее горизонтальную длину. На схему наносят также пункты геодезической сети, к которым осуществлялась привязка теодолитных ходов (В, 1).

Вычислительные работы по определению координат вершин теодолитного хода включают в себя: 1. Обработку угловых измерений и вычисление дирекционных углов сторон; 2. Вычисление приращений координат; 3. Вычисление координат вершин хода.

Все вычисления ведутся в специальной ведомости. В ведомость выписывают все исходные данные и начинают обработку.

 

 

·        ПОСТРОЕНИЕ ПЛАНА ТЕОДОЛИТНОЙ СЪЁМКИ

В ходе камеральных работ осуществляют: проверку журналов измерений и абрисов; обработку и уравнивание угловых измерений теодолитных ходов; уравнивание приращений координат и вычисление координат съемочных точек и составление ведомости координат; построение координатной сетки на чертежной бумаге; подготовку ситуационного плана местности в заданном масштабе.

Перед нанесением на план точек съемочного обоснования и ситуационных точек на листе ватмана строят координатную сетку с использованием для этой цели металлической топографической линейки Дробышева (ЛТ-1) или линейки ЛБЛ (рис.8).

Схема построения координатной сетки с помощью топографической линейки представлена на рисунке 8.

 

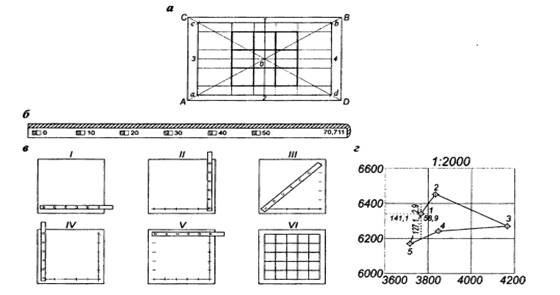
Рис. 8 – Схема построение координатной сетки

 

В положении линейки I , разместив ее параллельно нижнему краю листа ватмана, отмечают остро отточенным карандашом по вырезам 6 чёрточек. В положении линейки II совмещают центр первого выреза с шестым штрихом линии, полученной в положении I , и, разместив линейку приблизительно параллельно правому краю листа ватмана, по вырезам отмечают 5 дуг. Затем в положении III совмещают центр первого выреза с черточкой в начале прямой, полученной в положении I , и концом линейки засекают последнюю дугу, полученную в положении II , и таким образом получают первый прямоугольный треугольник. Далее строят второй прямоугольный треугольник (положения IV и V) и, соединив одноименные точки, расположенные на противоположных сторонах полученного прямоугольника, получают координатную сетку (VI) .

 Аналогичным образом строят координатную сетку и с помощью топографической линейки ЛБЛ, но с размерами сетки квадратов по 8 см. Полученную координатную сетку оцифровывают в абсолютной зональной или произвольной системе прямоугольных координат.

 Вершины и стороны основного хода, вершины диагонального хода и ситуация вычерчиваются на плане чертежной тушью. Стороны диагонального хода не вычерчиваются.  Пересечение линий координатной сетки вычерчиваются крестом зеленой тушью, размером 6×6 мм. Выходы линий координатной сетки у рамок плана подписываются черной тушью.

 План должен быть оформлен в соответствии с «Условными знаками для топографических планов масштабов 1:5000, 1:2000,1:1000, 1:500».

 

 

 

 

 

·        ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА

Тахеометрическая съемка — один из видов топографи­ческой съемки, выполняемой с помощью геодезических приборов — тахеометров. Слово «тахеометрия» означает быстрое измерение. Быстрота тахеометрической съемки достигается благодаря тому, что при одном наблюдении съемочного пикета получают данные, необходимые для определения как планового, так и высотного его положе­ния .

Тахеометрическая съемка имеет ряд преимуществ перед другими видами наземных съемок в условиях, когда полевые работы необходимо выполнять в сравни­тельно короткий срок или нет благоприятной погоды для выполнения съемки другими методами.

В основе тахеометрической съемки лежит идея определения пространственного положения точки местности одним наведением зрительной трубы прибора на рейку, установленную в этой точке.

Положение точки К на рис. 6.2 над условной плоскостью Р по высоте и относительно стороны съемочного обоснования АВ в плане определяется путем:

-измерения теодолитом горизонтального угла β между стороной съемочного обоснования АВ и направлением на точку местности К;

- измерения наклонного расстояния D оптическим дальномером;

- измерения угла наклона V теодолитом;

Рис. 6.2. Геометрические построения тахеометрической

съемки.

- расчета горизонтального проложения d = D cos²V;

- расчета превышения h точки К над плоскостью Р :

h = dtgV + i – l, где i – высота прибора, l – высота наведения средней нити сетки на рейку.

Тахеосъемка, таким образом, объединяет в себе два процесса: съемку ситуации и съемку рельефа. Кроме того, само съемочное обоснование также может определяться в процессе тахеосъемки. Тахеосъемка выполняется обычно в крупных масштабах 1:500 – 1: 5000 на небольших участках местности и вдоль трасс линейных сооружений (дорог, каналов и т.п.). Важное достоинство тахеосъемки заключается в возможности существенную долю объема работ по составлению планов, карт и ЦММ перенести в камеральные условия, где возможно широкое применение ЭВМ. В этой связи особенно эффективно использование для тахеосъемки электронных тахеометров с записью результатов измерений на магнитные носители информации.

Недостатком тахеосъемки является то, что при камеральной обработке результатов и создании карт, планов и ЦММ практически исключается возможность сличения их с местностью. В связи с этим могут быть пропущены некоторые ее существенные детали, не снятые исполнителями, либо «выпавшие» в результате ошибок при камеральной обработке.

При производстве тахеосъемки в настоящее время используются следующие приборы:

- оптические теодолиты Т15, Т15К, Т30, 2Т30, 2Т30П и другие;

- номограммные тахеометры ТН, DALTA-010; DALTA-020 и др.;

- электронные тахеометры Та-3, Та-5, RECOTA, RETA и др.;

- рейки обычные нивелирные, рейки тахеометрические для номограммных тахеометров;

- вехи обычные и тахеометрические – с отражателями для светодальномеров в электронных тахеометрах;

- ленты землемерные ЛЗ, ЛЗШ (для съемки подробностей ситуации);

- рулетки тесьмяные РТ (для съемки подробностей ситуации).

·        ПРОИЗВОДСТВО ТАХЕОМЕТРИЧЕСКОЙ СЪЕМКИ.

ПОЛЕВЫЕ РАБОТЫ

В процессе полевых работ при тахеометрической съемке выполняются следующие операции:

- рекогносцировка участка съемки, определение и закрепление точек съемочного обоснования. Указанные точки выбираются, как правило, на возвышенных местах и расстояние между ними должно быть не более 350 м и не менее 20 м;

- определение планово-высотных координат точек обоснования.

Выполняется либо специально, в этом случае расстояния между точками измеряются мерными лентами в прямом и обратном направлениях или светодальномерами, а превышения определяются методом геометрического нивелирования, либо непосредственно в процессе съемки. В последнем случае расстояния измеряются оптическими или светодальномерами, а превышения – методом тригонометрического нивелирования. Расстояния и превышения измеряются дважды – из каждой точки обоснования на переднюю и на заднюю соседние. В обоих случаях создания съемочного обоснования кроме указанных измерений выполняют также измерения полным приемом правых по ходу лежащих горизонтальных углов;

- съемка «реечных» точек – характерных точек ситуации и рельефа. Эта съемка производится следующим образом. Теодолит устанавливается и центрируется над точкой съемочного обоснования.

Лимб теодолита ориентируется на переднюю (иногда заднюю) точку съемочного обоснования. Далее на реечных точках устанавливают рейку, причем реечные точки не подлежат никакому закреплению на местности и рейку ставят непосредственно на землю. Наводят трубу на рейку в заданной точке и берут отсчеты по лимбу, вертикальному кругу и определяют расстояние до точки дальномером. Реечные точки размещаются по снимаемой территории по возможности равномерно так, чтобы расстояние между ними не превышало величин (рис. 6.3):

Масштаб 1: 500 1: 1000 1: 2000 1: 5000

Расст., м 10 20 50 100 ;

- в процессе тахеосъемки на каждой станции (точке съемочного обоснования) ведется схематический чертеж местности – абрис. На нем показываются все реечные точки, снятые с данной станции, направления слонов и контуры ситуации (рис. 6.4). Абрис является очень важным полевым документом тахеосъемки.

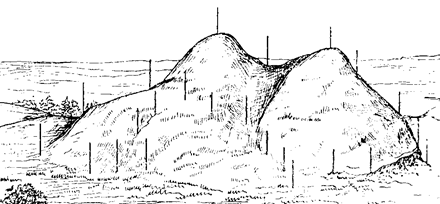
Рис. 6.3. Реечные точки при тахеометрической съемке.

а)

б)

Рис. 6.4. Примеры абрисов тахеометрической съемки.

А) – сельская местность, б) – морская набережная.

Данные всех полевых измерений записывают в журнал установленной формы – журнал тахеометрической съемки.

 

ПОСТРОЕНИЕ ПРОФИЛЯ ПО РЕЗУЛЬТАТАМ ТРАССИРОВАНИЯ

СОДЕРЖАНИЕ И ТЕХНОЛОГИЯ РАБОТ ПО ПОЛЕВОМУ ТРАССИРОВАНИЮ

·        ГЕОДЕЗИЧЕСКИЕ РАБОТЫ ПРИ ПОЛЕВОМ ТРАССИРОВАНИИ

В процессе полевого трассирования, вариант трассы переносится на местность по координатам начала и конца трассы и углов поворота. Вдоль трассы прокладывается опорный теодолитный ход (не обязательно непосредственно по трассе).

Кроме того, вдоль трассы – непосредственно по ее оси разбивается так называемый пикетаж. Он включает в себя следующие элементы:

1. Закрепление на местности (столбами, бетонными блоками, специальными марками и т.п.) точек начала и конца проектного варианта трассы.

2. Закрепление на местности деревянными кольями – «пикетами» отрезков по расстоянию через каждые 100 м. Пикеты сокращенно обозначаются ПК0, ПК1, … ПК8 и т.д. При таком обозначении номер пикета обозначает расстояние в сотнях метров от начала трассы до данного пикета.

3. Кроме пикетов, кольями закрепляются также перегибы рельефа местности, пересечения трассы дороги с реками, ручьями, мостами, подземными и надземными коммуникациями и т.п., а также точки поворота трассы – вершины углов ВУ. Эти точки называются «плюсовыми» и обозначаются как номер младшего по расстоянию пикета плюс расстояние до данной точки от этого пикета, например ПК21+55, означает, что «плюсовая» точка находится на расстоянии 2 км и 155 м от начала трассы или в 55 м от ПК21.

4. Аналогично «плюсовым» точкам закрепляются также так называемые «главные» точки кривых (круговых или переходных) НК, СК, КК. Однако здесь есть определенные сложности, связанные с расстояниями. Дело в том, что первоначально трасса прокладывается по ломаной линии, а затем на местность нужно перенести ее кривые вставки, а вставки сокращают длину трассы т.к. кривая короче ломаной.

Таким образом, длина трассы сокращается на величины домеров Д. Это необходимо учитывать в общей длине трассы т. К. разность ломаной и кривой может достигать нескольких км.

Рассмотрим перенос на местность основных точек круговых кривых (что наиболее просто), а также пикетов, попавших на тангенсы круговых кривых.

Вынос основных точек кривых на местность и затем пикетов на кривые (после разбивки теодолитом каждого угла поворота трассы) заключается в следующем:

- расчет основных элементов кривой по формулам, приведенным выше (задать Q и R, рассчитать К, Т, Д, Б);

- рассчитать пикетное положение НК = ВУ-Т;

- рассчитать пикетное положение КК = НК+К;

- рассчитать пикетное положение СК = НК+К/2;

- отмерить от ВУ расстояние Т «назад» по трассе (или вперед от ближайшего пикета, меньшего НК) и закрепить НК;

- отмерить от ВУ расстояние Т «вперед» по трассе и закрепить КК;

- из ВУ отложить теодолитом угол Q/2, по лучу отложить Б и

закрепить СК;

- проверить условие: пикетное положение

КК = НК + К = НК + Т + Т – Д;

- если какой-либо пикет оказался на тангенсе, то он должен быть перенесен на кривую. Это делается методом прямоугольных координат с началом в точке начала или конца кривой (рис. 12.3).

Рис. 12.3. Схема выноса пикета на кривую.

Координаты Х и Y вычисляют по формулам:

X = Rsin(φ),

Y = 2Rsin²(φ/2), (12.3.1)

φ⁰ = L x 180⁰/(πR),

где L – расстояние по кривой между данным пикетом N и началом кривой НК или между пикетом и концом кривой КК.

В местах характерного изменения рельефа, перпендикулярно трассе разбивают поперечники по 25 м в обе стороны от трассы. Точку пересечения поперечника с трассой закрепляют как плюсовую точку (например, ПК12+65.74). Еще ряд точек закрепляют на поперечниках, измеряя при этом расстояния от трассы до данной точки поперечника. Обозначение точек поперечника состоит из двух частей: обозначения точки пересечения с трассой и расстояния вправо или влево от трассы по поперечнику. Например: ПК12+65.74 Л12.60, ПК12+65.74 П22.42 означает, что точки находятся на поперечнике, пересекающем трассу в точке ПК12+65.74 и расположены от трассы влево на расстоянии 12.60 м и вправо на расстоянии 22.42 м соответственно.

В процессе разбивки пикетажа ведут пикетажный журнал (рис. 12.4). Его изготавливают из миллиметровой бумаги в виде блокнота, размером 20 х 10 см. Ведут пикетажный журнал в масштабе 1:200 – 1: 2000 в зависимости от сложности рельефа и ситуации.

Рис. 12.4. Страница пикетажного журнала.

В пикетажный журнал заносят:

- направление трассы в виде прямой линии, на которую наносят пикетные и плюсовые точки;

- вершины углов поворота трассы, в которых стрелками вправо или влево показывают изменение направления трассы, величины углов поворота, элементы кривых и их пикетное положение;

- результаты глазомерной съемки ситуации в полосе шириной 50 м (по 25 м вправо и влево от трассы);

- схему высотной привязки трассы к реперам (если она производилась).

Нивелирование трассы производится методом геометрического нивелирования из середины с контролем в виде замкнутого хода (“прямо” и “обратно”). Нивелированию в прямом ходе полежат точки пикетов, главные точки кривых, плюсовые точки и точки поперечников. При этом, как правило, в прямом ходе точки пикетов являются связующими, а остальные – промежуточными. При сложном рельефе связующими могут быть и плюсовые точки трассы. В обратном ходе связующими могут быть любые удобные точки местности. Плюсовые и другие пикетные точки в обратном ходе могут не нивелироваться.

В процессе камеральных работ производится обработка журнала нивелирования, построение продольного и поперечного профилей трассы, плана трассы, а также составляется ведомость углов поворота, прямых и кривых.

·        ПОСТРОЕНИЕ ПРОФИЛЯ ПО РЕЗУЛЬТАТАМ ПОЛЕВОГО ТРАССИРОВАНИЯ. ОПРЕДЕЛЕНИЕ ПРОЕКТНЫХ ЭЛЕМЕНТОВ ТРАССЫ

11. Линейными называются сооружения, имеющие значительную протяженность, но занимающие сравнительно узкую полосу земной поверхности.

Для проектировании таких сооружений необходимо иметь продольные профили их трассы, поперечные профили и контурный план полосы местности, занимаемой сооружением.

Линейные сооружения проектируют в две стадии: технический проект и рабочий проект. Для технического проекта выполняют камеральное трассирование (намечают положение оси проектируемого сооружения) по имеющимся топографическим планам и картам возможно крупного масштаба или фотопланом, затем предварительные изыскания по предложенным нескольким вариантам.

2. Подготовка к нивелированию трассы состоит в следующем. Ось сооружения в плане определяют проложением по ней теодолитного хода между начальной и конечной точками трассы. В зависимости от длины конечные точки трассы привязывают к имеющимся пунктам геодезического обоснования. Углы поворота трассы закрепляют на местности прочными знаками. В теодолитном ходе по оси сооружения отмечают через каждые 100 м точки, называемые пикетами, закрепляя их кольями со сторожками, на боковой грани которых указывают номера пикетов. Начало трассы обозначают нулевым пикетом (ПКО), а последующие ПК1, ПК2 и т.д.

Углы поворота трассы обозначают возрастающими номерами; им присваивают обозначение, состоящее из порядкового номера заднего пикета плюс расстояние от него до угла поворота. Номер вершины угла пишут в числителе, а пикетажное обозначение – в знаменателе.

Одновременно на местности размечают поперечники. Расстояния между поперечниками и их длину указывают в техническом задании для наилучшего выявления рельефа. По трассе и поперечникам в характерных местах излома рельефа назначают плюсовые точки. Нумерация их идет от предшествующего пикета плюс расстояние от него до плюсовой точки. На поперечниках нумерация плюсовых точек складывается из номера пикета и расстояния от оси трассы с указанием части поперечника (правой – ПР или левой – Л). При построении пикетажа ведут пикетажный журнал. Съемку ситуации производят одновременно с построением пикетажа.

12. При нивелировании пикетажа нивелир устанавливают на равные расстояния от нулевого и первого пикетов и берут отсчеты по рейкам, устанавливаемым на пикетах, а затем на плюсовых точках по продольной оси к поперечникам и главных точках кривых.

Аналогично нивелируют и на следующих станциях. Пикеты нивелируют и в обратном направлении (для контроля). Начальную и конечную точки трассы привязывают в высотном положении к пунктам имеющихся опорных геодезических сетей.

13. Данные нивелирования точек пикетажа по оси трассы и поперечникам записывают в «Журнал нивелирования по пикетажу».

Отметки связующих точек вычисляют по способу превышений, а отметки плюсовых точек рациональнее вычислять по горизонту инструмента.

Для проверки правильности вычислений на каждой странице производят «постраничный контроль», для чего подсчитывают суммы отсчетов по задним и передним рейкам, суммы положительных и отрицательных превышений. Записывают разность сумм задних и передних отчетов и алгебраическую сумму превышения. Обе эти величины должны быть равны между собой и равняться двойной величине суммарного превышения для станций, записанных на данной странице.

14. После вычисления отметок всех пикетов и плюсовых точек на основе журнала нивелирования по пикетажу и пикетажного журнала строят профиль.

Профиль строят на миллиметровой бумаге. Масштаб для составления продольных профилей для горизонтальных расстояний принимают по техническому заданию (обычно 1:500 – 1:5000), а масштаб для вертикальных расстояний (отметок) принимают, как правило, в десять раз крупнее. Для составления поперечных профилей обычно масштабы для горизонтальных и вертикальных расстояний (отметок) принимают те же, что и для вертикальных расстояний продольного профиля.

Сетка профиля может быть различной в зависимости от спецификации сооружений линейного типа и приемов проектирования.

Составление продольного профиля начинают с обозначения вертикалями всех пикетов, через 100 м в принятом масштабе. Затем размечают все плюсовые точки. Против каждой вертикали выписывают вертикально черные отметки соответственных точек. После этого расчерчивают полную сетку граф профиля тонкими линиями на всю протяженность трассы. Верхнюю линию графы «развернутый план местности» принимают за линию условного горизонта. Ей придают условную отметку, кратную 10 м, и такую, чтобы самая низкая точка трассы не приближалась к линии условного горизонта ближе чем на 4 – 5 см. После заготовки сетки профиля по вертикальным линиям миллиметровой бумаги откладывают отметки всех точек трассы, так называемые фактические отметки (отметки пронивелированной существующей поверхности), и накладывают карандашом точки. Соединяя эти точки прямыми ломаными линиями, получают фактическую линию профиля, представляющую собой уменьшенное изображение вертикального разреза местности по оси проектируемого сооружения.

Следует помнить, что все отметки (черные, красные, рабочие) на профиль выписывают с округлением до сантиметров.

Поперечные профили целесообразнее располагать над соответственными пикетами продольного профиля, что создает определенную наглядность для проектировщика. Если такой возможности не представляется, поперечные профили располагают один под другим в правой части листа миллиметровой бумаги.

15. Для всех пронивелированных точек перелома рельефа местности по оси сооружения и поперечникам определяют и записывают их проектные (красные) отметки (отметки проектируемой поверхности).

Наметив проектную линию графически по миллиметровой бумаге, рассчитывают от линии условного горизонта красные отметки точек перелома проектной линии, находят превышения смежных точек и горизонтальные расстояния между ними и вычисляют получающиеся уклоны проектной линии. Если уклоны допустимы, их записываю в графу «уклоны», выражая запись дробью. Черта дроби показывает направление уклона по ходу трассы: направленная вверх обозначает положительный уклон, вниз – отрицательный; горизонтальная черта обозначает нулевой уклон.

Красные отметки всех пикетов и плюсовых точек проектной линии вычисляют только по уклонам аналитически по формуле

Н_В = Н_А + id

Причем проектные отметки точек на каждом наклонном участке следует вычислять последовательно нарастающим порядком, каждый раз от начальной точки участка.

После вычисления красных отметок определяют и выписывают на профиль рабочие отметки, являющиеся разностями между черными и красными отметками и показывающие высоты насыпей или глубины выемок.

 

 

 

Список использованных источников

1.     Геодезия: Учебник для среднего профессионального образования. / М.М. Киселев, Д.Ш. Михелев. 2-е издание, переработка и дополнение. - М. : Издательский центр «Академия», 2012. – 384 с.

2.     Инженерная геодезия: Учебник для вузов / Е.Б. Клюшин, М.И. Киселев, Д.Ш. Михелев, В.Д. Фельдман; Под. ред. Д.Ш. Михелева – 6-е издание, испр. – М. : Издательский центр «Академия», 2011. – 280с.

3.     Практикум по геодезии: Учебное пособие для вузов, Под ред. Г.Г. Поклада. – М.: Академический проект; Трикеба, 2011. – 470с. 

4.     Интернет ресурсы:  Публичная электронная библиотека

 Режим доступа: http://lib.chistopol.net/library/book/14741.html

5.     Библиотека гостов и нормативных документов

Режим доступа:  http://libgost.ru/gost/

 

 

Скачано с www.znanio.ru