
Содержание
|
1. Статика: основные понятия и аксиомы. |
|
|
1.1. Теоретические сведения |
3 |
|
1.2. Примеры решения практических задач |
13 |
|
2. Кинематика: основные понятия. |
|
|
2.1. Теоретические сведения |
16 |
|
2.2. Примеры решения практических задач |
20 |
|
3. Динамика: основные понятия и аксиомы |
|
|
3.1. Теоретические сведения |
21 |
|
3.2. Примеры решения практических задач |
|
|
Список литературы |
|
1. Статика: основные понятия и аксиомы.
1.1 Теоретические сведения
Статика – раздел теоретической механики, в котором рассматривают свойства сил, приложенных к точкам твердого тела, и условия их равновесия. Основные задачи:
1. Преобразования систем сил в эквивалентные системы сил.
2. Определение условий равновесия систем сил, действующих на твердое тело.
Материальной точкой называют простейшую модель материального тела
любой формы, размеры которого достаточно малы и которое можно принять за геометрическую точку, имеющую определенную массу. Механической системой называется любая совокупность материальных точек. Абсолютно твёрдым телом называют механическую систему, расстояния, между точками которой не изменяются при любых взаимодействиях.
Сила – это мера механического взаимодействия материальных тел между собой. Сила – величина векторная, так как она определяется тремя элементами:
· численным значением;
· направлением;
· точкой приложения (А).
Единица измерения силы – Ньютон(Н).

Рисунок 1.1
Система сил – это совокупность сил, действующих на какое – либо тело.
Уравновешенной (равной нулю) системой сил называется, такая система, которая будучи, приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Аксиомы статики.
Аксиома 1: Если к телу приложена уравновешенная система сил, то оно движется равномерно и прямолинейно или находится в состоянии покоя (закон инерции).
 Аксиома 2: Абсолютно твердое тело
находится в равновесии под действием двух сил тогда и только тогда, когда эти
силы равны по модулю, действуют по одной прямой и направлены в противоположные
стороны. Рисунок 1.2
Аксиома 2: Абсолютно твердое тело
находится в равновесии под действием двух сил тогда и только тогда, когда эти
силы равны по модулю, действуют по одной прямой и направлены в противоположные
стороны. Рисунок 1.2
 Аксиома 3: Механическое состояние
тела не нарушится, если к действующей на него системе сил добавить или от неё
отнять уравновешенную систему сил.
Аксиома 3: Механическое состояние
тела не нарушится, если к действующей на него системе сил добавить или от неё
отнять уравновешенную систему сил.
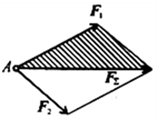
Аксиома 4: Равнодействующая двух приложенных к телу сил равна их геометрической сумме, то есть выражается по модулю и направлению диагональю параллелограмма, построенного на этих силах как на сторонах.
Рисунок 1.3.
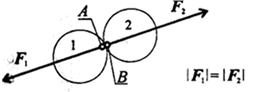 Аксиома 5: Силы, с которыми
действуют друг на друга два тела, всегда равны по модулю и направлены вдоль
одной прямой в противоположные стороны.
Аксиома 5: Силы, с которыми
действуют друг на друга два тела, всегда равны по модулю и направлены вдоль
одной прямой в противоположные стороны.
Рисунок 1.4.
Виды связей и их реакции
Связями называются любые ограничения,
препятствующие перемещению тела в пространстве. Тело, стремясь под действием
приложенных сил осуществить перемещение, которому препятствует связь, будет
действовать на нее с некоторой силой, называемой силой давления на связь. По закону о равенстве действия и
противодействия, связь будет действовать на тело с такой же по модулю, но
противоположно направленной силой.
Сила, с которой данная связь действует на тело, препятствуя тем или иным
перемещениям, называется силой реакции (реакцией) связи.
Одним из основных положений механики является принцип освобождаемости от связей: всякое несвободное тело можно рассматривать как
свободное, если отбросить связи и заменить их действие реакциями связей.
Реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу. Основные виды связей и их реакции приведены в таблице 1.1.
Таблица 1.1
Виды связей и их реакции
|
№ |
Наименование связи |
Условное обозначение |
|
1 |
Гладкая поверхность (опора) – поверхность
(опора), трением о которую данного тела можно пренебречь. |
|
|
2 |
Нить (гибкая, нерастяжимая). Связь, осуществлённая в виде нерастяжимой нити, не позволяет телу удаляться от точки подвеса. Поэтому реакция нити направлена вдоль нити к точке её подвеса. |
|
|
3 |
Невесомый стержень –
стержень, весом которого по сравнению с воспринимаемой нагрузкой можно
пренебречь. |
|
|
4 |
Подвижный шарнир, шарнирно-подвижная опора. Реакция направлена по нормали к опорной поверхности. |
|
|
7 |
Жесткая заделка. В плоскости жесткой
заделки будут две составляющие реакции |
|
Система сходящихся сил
Системой
сходящихся сил называется система сил, линии
действия которых пересекаются в одной точке. Две силы, сходящиеся в одной
точке, согласно третьей аксиоме статики можно заменить одной силой –равнодействующей.
Главный вектор системы сил –
величина, равная геометрической сумме сил системы.
Равнодействующую плоской системы сходящихся сил можно определить графически и аналитически.
Сложение системы сил. Сложение плоской системы сходящихся сил осуществляется либо путём последовательного сложения сил с построением промежуточной равнодействующей (рис. 1.5), либо путём построения силового многоугольника (рис. 1.6).
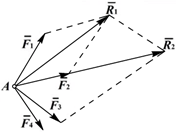
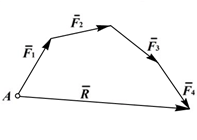
Рисунок 1.5Рисунок 1.6
Проекция
силы на ось – алгебраическая величина, равная
произведению модуля силы на косинус угла между силой и положительным
направлением оси.
Проекция Fx (рис.1.7) силы ![]() на ось х положительна, если угол α острый,
отрицательна - если угол α тупой. Если сила
на ось х положительна, если угол α острый,
отрицательна - если угол α тупой. Если сила ![]() перпендикулярна оси, то ее проекция на
ось равна нулю.
перпендикулярна оси, то ее проекция на
ось равна нулю.
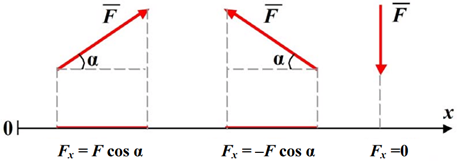
Рисунок 1.7
Проекция силы ![]() на плоскость Оху – вектор
на плоскость Оху – вектор ![]() , заключенный между
проекциями начала и конца силы
, заключенный между
проекциями начала и конца силы ![]() на эту плоскость. Т.е. проекция силы
на плоскость величина векторная, характеризуется не только числовым значением,
но и направлением в плоскости Оху (рис.1.8).
на эту плоскость. Т.е. проекция силы
на плоскость величина векторная, характеризуется не только числовым значением,
но и направлением в плоскости Оху (рис.1.8).
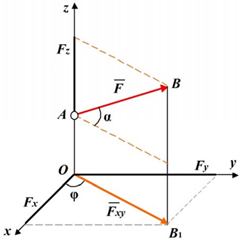
Рисунок 1.8
Тогда модуль
проекции ![]() на плоскость Оху будет равен:
на плоскость Оху будет равен:
Fxy = F cosα,
где α -
угол между направлением силы ![]() и ее проекцией
и ее проекцией ![]() .
.
Аналитический способ задания сил. Для аналитического
способа задания силы ![]() необходимо выбрать систему
координатных осей Охуz,
по отношению к которой будет определяться направление силы в пространстве.
необходимо выбрать систему
координатных осей Охуz,
по отношению к которой будет определяться направление силы в пространстве.
Вектор, изображающий силу ![]() , можно построить, если
известны модуль этой силы и углы α, β, γ, которые сила образует
с координатными осями. Точка А приложения силы
, можно построить, если
известны модуль этой силы и углы α, β, γ, которые сила образует
с координатными осями. Точка А приложения силы ![]() задается отдельно своими координатами х, у, z. Можно задавать силу ее
проекциями Fx, Fy, Fz на координатные оси. Модуль силы в
этом случае определится по формуле:
задается отдельно своими координатами х, у, z. Можно задавать силу ее
проекциями Fx, Fy, Fz на координатные оси. Модуль силы в
этом случае определится по формуле:
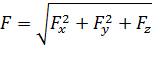
а направляющие косинусы:
 ,
,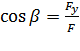
 .
.
Аналитический способ сложения сил:проекция вектора суммы на какую нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось, т.е., если:
,![]()
то ,![]() ,
,![]()
![]() .
.
Зная Rx, Ry, Rz, можем
определить модуль

и направляющие косинусы:
 ,
, 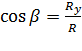 ,
, 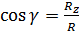 .
.
Рисунок 1.9
Для равновесия системы
сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была
равна нулю.
1) Геометрическое условие
равновесия сходящейся системы сил: для равновесия системы сходящихся
сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих
сил,
был замкнут (конец вектора последней слагаемой
силы должен
совместиться с началом вектора первой слагаемой силы). Тогда главный вектор системы
сил будет равен нулю (![]() )
)
2) Аналитические условия
равновесия. Модуль главного вектора системы сил определяется по
формуле .![]() =0. Поскольку
=0. Поскольку ![]() , то подкоренное выражение
может быть равно нулю только в том случае, если каждое слагаемое одновременно
обращается в нуль, т.е.
, то подкоренное выражение
может быть равно нулю только в том случае, если каждое слагаемое одновременно
обращается в нуль, т.е.
Rx = 0, Ry = 0, Rz = 0.
Следовательно, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трёх координат осей были равны нулю:

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил на каждую из двух координатных осей были равны нулю:
![]()
 Сложение двух параллельных сил, направленных в
одну сторону.
Сложение двух параллельных сил, направленных в
одну сторону.
Рисунок 1.9
Две
параллельные силы, направленные в одну сторону, приводятся к одной
равнодействующей силе, им параллельной и направленной в ту же сторону. Величина
равнодействующей равна сумме величин данных сил, а точка ее приложения С делит
расстояние между линиями действия сил внутренним образом на части, обратно
пропорциональные величинам этих сил, то есть
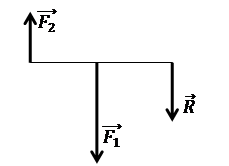
![]() R=F1+F2
R=F1+F2
![]()
Сложение двух не равных по величине параллельных сил, направленных в противоположные стороны.
![]()
![]() Две не
равные по величине антипараллельные силы приводятся к одной равнодействующей
силе им параллельной и направленной в сторону большей силы. Величина равнодействующей
равна разности величин данных сил, а точка ее приложения С, делит расстояние
между линиями действия сил внешним образом на части, обратно пропорциональные
величинам этих сил, то есть
Две не
равные по величине антипараллельные силы приводятся к одной равнодействующей
силе им параллельной и направленной в сторону большей силы. Величина равнодействующей
равна разности величин данных сил, а точка ее приложения С, делит расстояние
между линиями действия сил внешним образом на части, обратно пропорциональные
величинам этих сил, то есть
Пара сил и момент силы относительно точки.
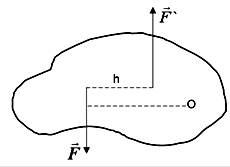 Моментом силы
Моментом силы ![]() относительно точки О
называется, взятое с соответствующим знаком, произведение величины силы на
расстояние h от точки О до линии действия силы
относительно точки О
называется, взятое с соответствующим знаком, произведение величины силы на
расстояние h от точки О до линии действия силы ![]() . Это произведение берётся со
знаком плюс, если сила
. Это произведение берётся со
знаком плюс, если сила ![]() стремится вращать тело против
хода часовой стрелки, и со знаком -, если сила
стремится вращать тело против
хода часовой стрелки, и со знаком -, если сила ![]() стремится вращать тело по ходу
часовой стрелки, то есть
стремится вращать тело по ходу
часовой стрелки, то есть ![]() . Длина перпендикуляра h
называется плечом силы
. Длина перпендикуляра h
называется плечом силы![]() точки О. Эффект действия силы
т.е. угловое ускорение тела больше, чем больше величина момента силы.
точки О. Эффект действия силы
т.е. угловое ускорение тела больше, чем больше величина момента силы.
Рисунок 1.11
Парой
сил
называется система, состоящая из двух равных по величине параллельных сил,
направленных в противоположные стороны. Расстояние h между линиями действия сил
называется плечом пары. Моментом пары сил m(F,F') называется
взятое с соответствующим знаком произведение величины одной из сил,
составляющих пару на плечо пары.
Записывается это так: m(F, F')= ± F × h , где произведение берется со знаком плюс, если пара сил стремится вращать тело против хода часовой стрелки и со знаком минус, если пара сил стремится вращать тело по ходу часовой стрелки.
Теорема о сумме моментов сил пары.
Сумма моментов сил пары (F,F') относительно любой точки 0, взятой в плоскости действия пары, не зависит от выбора этой точки и равна моменту пары.
Теорема об эквивалентных парах. Следствия.
Теорема. Две пары, моменты которых равны между собой, эквивалентны, т.е. (F, F') ~ (P,P')
Следствие 1. Пару сил можно переносить в любое место плоскости ее действия, а также поворачивать на любой угол и изменять плечо и величину сил пары, сохраняя при этом момент пары.
Следствие 2. Пара сил не имеет равнодействующей и не может быть уравновешена одной силой, лежащей в плоскости пары.
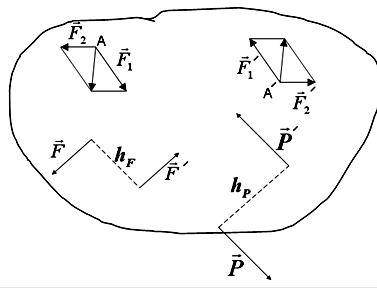
Рисунок 1.12
Сложение и условие равновесия системы пар на плоскости.
1. Теорема о сложении пар, лежащих в одной плоскости. Систему пар, как угодно расположенных в одной плоскости, можно заменить одной парой, момент которой равен сумме моментов данных пар.
2. Теорема о равновесии системы пар на плоскости.
![]() Для того, чтобы абсолютно
твердое тело находилось в состоянии покоя под действием системы пар, как угодно
расположенных в одной плоскости, необходимо и достаточно, чтобы сумма моментов
всех пар была равна нулю, то есть
Для того, чтобы абсолютно
твердое тело находилось в состоянии покоя под действием системы пар, как угодно
расположенных в одной плоскости, необходимо и достаточно, чтобы сумма моментов
всех пар была равна нулю, то есть
Центр тяжести
Сила тяжести – равнодействующая сил притяжения к Земле, распределённых по всему объему тела.
Центр тяжести тела – это такая неизменно связанная с этим телом точка, через которую проходит линия действия силы тяжести данного тела при любом положении тела в пространстве.
Методы нахождения центра тяжести
1. Метод симметрии:
1.1. Если однородное тело имеет плоскость симметрии, то центр тяжести лежит в этой плоскости
1.2. Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси. Центр тяжести однородного тела вращения лежит на оси вращения.
1.3 Если однородное тело имеет две оси симметрии, то центр тяжести находится в точке их пересечения.
2. Метод разбиения: Тело разбивается на наименьшее число частей, силы тяжести и положение центров тяжести которых известны.
3. Метод отрицательных масс: При определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но массу свободных полостей считать отрицательной.
Координаты центра тяжести плоской фигуры:
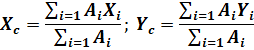
Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам. (рисунок 1.13)

Примечание: Центр тяжести симметрии фигуры находится на оси симметрии.
Центр
тяжести стержня находится на середине высоты.
1.2. Примеры решения практических задач
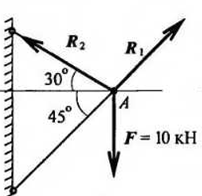 Пример
1:Груз
подвешен на стержне и находится в равновесии. Определить усилия в стержне.
(рисунок 1.2.1)
Пример
1:Груз
подвешен на стержне и находится в равновесии. Определить усилия в стержне.
(рисунок 1.2.1)
Решение:
1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз. ( 5-я аксиома)
Определяем возможные направления реакций связей «жесткие стержни».
Усилия направлены вдоль стержней.
2.
Рисунок
1.2.1.
Освободим
точку А от связей, заменив действие связей их реакциями. (рисунок 1.2.2)
3.  Система
находится в равновесии. Построим треугольник сил.
Система
находится в равновесии. Построим треугольник сил.
Построение начнём с известной силы, вычертив вектор F в некотором масштабе.
Из конца вектора F проводим линии, параллельные реакциям R1 и R2.
Рисунок
1.2.2 
Пересекаясь,
линии создают треугольник. (рисунок 1.2.3.). Зная масштаб построений и измерив
длину сторон треугольника, можно определить величину реакций в стержнях.
4. Для более точных расчётов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла – величина постоянная
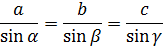
Для данного случая:
Рисунок
1.2.3
![]()
![]()
![]()
Замечание: Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.
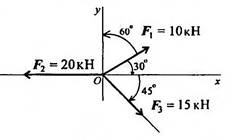 Пример
2: Определить
величину и направление равнодействующей плоской системы сходящихся сил
аналитическим способом.
Пример
2: Определить
величину и направление равнодействующей плоской системы сходящихся сил
аналитическим способом.
Решение:
Рисунок 1.2.4
1.
Определяем проекции всех сил системы на Ох (рисунок 1.2.4)
![]()
![]()
![]()
Сложив алгебраически проекции, получим проекцию равнодействующей на ось Ох.
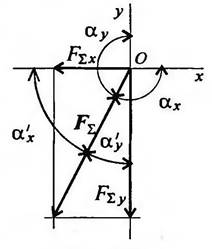
![]()
Знак говорит о том, что равнодействующая направлена влево.
2. Определяем проекции всех сил на ось Оу:
![]()
![]()
![]()
Сложив алгебраически проекции, получим проекцию равнодействующей на ось Оу.
![]()
Знак говорит о том, что равнодействующая направлена вниз.
3. Определяем модуль равнодействующей по величинам проекций:
![]()
4. Определим значение угла равнодействующей с осью Ох:
![]()
и значение угла с осью Оу:
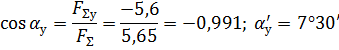
![]()
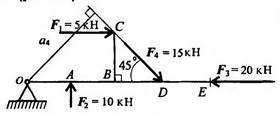 Пример
3: Расчитать
сумму моментов сил относительно точки О (рисунок 1.2.6).
Пример
3: Расчитать
сумму моментов сил относительно точки О (рисунок 1.2.6).
ОА=АВ=ВD=DE=CB=2м
|
Решение:
1. Момент силы относительно точки численно равен произведению модуля на плечо силы.
2. Момент силы равен нулю, если линия действия силы проходит через точку.
![]()
![]()
![]()
![]()
![]()
 Пример
4: Определить
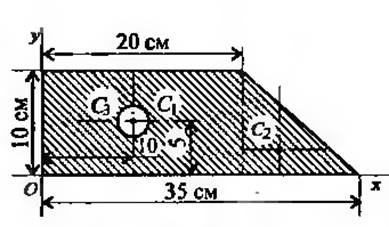
положение центра тяжести фигуры, представленной на рисунке 1.2.7
Пример
4: Определить
положение центра тяжести фигуры, представленной на рисунке 1.2.7
Решение:
Разбиваем фигуру на три:
1-прямоугольник
А1=10*20=200см2
2-треугольник
А2=1/2*10*15=75см2
3-круг
А3=3,14*32=28,3см2
ЦТ фигуры 1: х1=10см, у1=5см
ЦТ фигуры 2: х2=20+1/3*15=25см, у2=1/3*10=3,3см
ЦТ фигуры 3: х3=10см, у3=5см
![]()
Аналогично определяется ус=4,5см
2. Кинематика: основные понятия.
Основные кинематические параметры
Траектория - линия, которую очерчивает материальная точка при движении в пространстве. Траектория может быть прямой и кривой, плоской и пространственной линией.
Уравнение траектории при плоском движении: у = f (x)
Пройденный путь. Путь измеряется вдоль траектории в направлении движения. Обозначение - S, единицы измерения - метры.
Уравнение движения точки –это уравнение, определяющее положение движущейся точки в зависимости от времени.
Рисунок 2.1
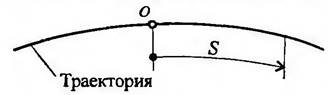 Положение точки в каждый момент времени можно определить по
расстоянию, пройденному вдоль траектории от некоторой неподвижной точки,
рассматриваемой как начало отсчета (рисунок 2.1). Такой способ задания движения
называется естественным. Таким образом, уравнение движения можно
представить в виде S = f (t).
Положение точки в каждый момент времени можно определить по
расстоянию, пройденному вдоль траектории от некоторой неподвижной точки,
рассматриваемой как начало отсчета (рисунок 2.1). Такой способ задания движения
называется естественным. Таким образом, уравнение движения можно
представить в виде S = f (t).
Рисунок 2.2
Положение
точки можно также определить, если известны ее координаты в зависимости от
времени (рисунок 2.2). Тогда в случае движения на плоскости должны быть заданы
два уравнения:
![]()
В случае пространственного движения добавляется и третья координата z=f3(t)
Такой способ задания движения называют координатным.
Скорость движения – это векторная величина, характеризующая в данный момент быстроту и направление движения по траектории.
 Скорость - вектор, в любой момент направленный по
касательной к траектории в сторону направления движения (рисунок 2.3).
Скорость - вектор, в любой момент направленный по
касательной к траектории в сторону направления движения (рисунок 2.3).
Рисунок 2.3
Если
точка за равные промежутки времени проходит равные расстояния, то движение
называют равномерным.
Средняя скорость на пути ΔS определяется:
![]()
где ΔS- пройденный путь за время Δt; Δt- промежуток времени.
Если точка за равные промежутки времени проходит неравные пути, то движение называют неравномерным. В этом случае скорость - величина переменная и зависит от времени v= f(t)
Скорость в данный момент определяют как
![]()
Ускорение точки - векторная величина, характеризующая быстроту изменения скорости по величине и направлению.
Скорость
точки при перемещении из точки М1 в точку Мг меняется по величине и
направлению. Среднее значение ускорения за этот промежуток времени ![]()
Ускорение
в данный момент: ![]()
Обычно для удобства рассматривают две взаимно перпендикулярные составляющие ускорения: нормальное и касательное (рисунок 2.4)
Нормальное ускорение аn, характеризует изменение скорости по
направлению
и определяется как ![]()
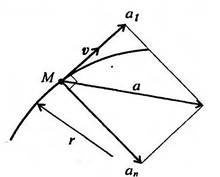 Нормальное ускорение всегда направлено перпендикулярно скорости
к центру дуги.
Нормальное ускорение всегда направлено перпендикулярно скорости
к центру дуги.
Рисунок 2.4
Касательное
ускорение аt ,
характеризует изменение скорости по величине и всегда направлено по касательной
к траектории; при ускорении его направление совпадает с направлением скорости,
а при замедлении оно направлено противоположно направлению вектора скорости.
![]()
Значение
полного ускорения определяется, как: ![]()
Анализ видов и кинематических параметров движений
Равномерное движение – это движение с постоянной скоростью:
![]()
Для прямолинейного равномерного движения:
![]()
Для криволинейного равномерного движения:
![]()
Закон
равномерного движения![]() :
:
Равнопеременное
движение – это движение с постоянным
касательным ускорением: ![]()
Для прямолинейного равнопеременного движения
![]()
Для криволинейного равнопеременного движения:
![]()
![]()
Закон равнопеременного движения:
![]()
Кинематические графики
Кинематические графики – это графики изменения пути, скорости и ускорений в зависимости от времени.
Равномерное движение (рисунок 2.5)

Рисунок 2.5
Равнопеременное движение (рисунок 2.6)

Рисунок 2.6
Простейшие движения твёрдого тела
Поступательным движением называют движение твёрдого тела, при котором всякая прямая линия на теле при движении остаётся параллельной своему начальному положению (рисунок 2.7)
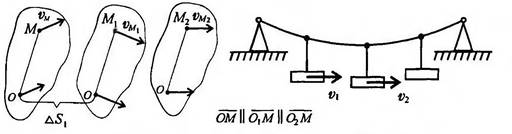
Рисунок 2.7
При поступательном движении все точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы.
 При вращательном
движении все точки тела описывают окружности вокруг общей неподвижной
оси.
При вращательном
движении все точки тела описывают окружности вокруг общей неподвижной
оси.
Неподвижная ось, вокруг которой вращаются все точки тела, называют осью вращения.
Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры. (рисунок 2.8)
φ – угол поворота тела;
ω – угловая скорость, определяет изменение угла поворота в единицу времени;
![]()
Изменение угловой скорости во времени определяется угловым ускорением:
![]()
2.2. Примеры решения практических задач
Пример 1: Дано уравнение движения точки. Определить скорость точки в конце третьей секунды движения и среднюю скорость за первые три секунды.
![]()
Решение:
1.
Уравнение скорости ![]()
2.
Скорость в конце третьей секунды (t=3c) ![]()
3.
Средняя скорость ![]()
Пример 2: По заданному закону движения определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
![]()
Решение:
1. Вид
движения: равнопеременное (![]() )
)
2.
При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчёта 10м;
- начальная скорость 20м/с
-
постоянное касательное ускорение ![]()
- ускорение отрицательное, следовательно, движение замедленное, ускорение направлено в сторону противоположную скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю.
![]()
3.Динамика: основные понятия и аксиомы
Динамика – раздел теоретической механики, в котором устанавливается связь между движение тел и действующими на них силами.
В динамике решают два типа задач:
· определяют параметры движения по заданным силам;
· определяют силы, действующие на тело, по заданным кинематическим параметрам движения.
Под материальной точкой
подразумевают некое тело, имеющее определенную массу (т. е. содержащее
некоторое количество материи), но не имеющее линейных размеров (бесконечно
малый объем пространства).
Изолированной
считается материальная точка, на которую не оказывают действие другие
материальные точки. В реальном мире изолированных материальных точек, как и
изолированных тел, не существует, это понятие является условным.
При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку.
Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка совпадает с центром тяжести тела.
При вращательном движении тела точки могут двигаться не одинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику материальной системы.
Аксиомы динамики
Первая аксиома (принцип инерции): всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Это состояние называют состоянием инерции. Вывести точку из этого состояния, т.е. сообщить ей некоторое ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.
Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг).
Вторая аксиома(второй закон Ньютона — основной закон динамики)
F=ma
где т — масса точки, кг; а — ускорение точки, м/с2.
Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли:
G = mg,
где g — 9,81 м/с² , ускорение свободного падения.
Третья аксиома(третий закон Ньютона): силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны.
![]()
При взаимодействии ускорения обратно пропорциональны массам.
Четвертая аксиома(закон независимости действия сил): каждая сила системы сил действует так, как она действовала бы одна.
Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности (рисунок 3.1):
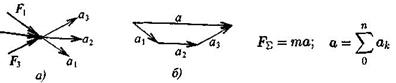
Рисунок 3.1
Понятие о трении. Виды трения.
 Трение-сопротивление
возникающее при движении одного шероховатого тела по поверхности другого. При
скольжении тел возникает трение скольжения, при качении – трение качания.
Трение-сопротивление
возникающее при движении одного шероховатого тела по поверхности другого. При
скольжении тел возникает трение скольжения, при качении – трение качания.
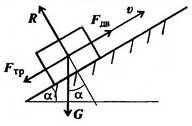
Трение скольжения
Рисунок 3.2.
Причина
– механическое зацепление выступов. Сила сопротивления движению при скольжении
называется силой трения скольжения (рисунок 3.2)
Законы трения скольжения:
 1. Сила трения скольжения прямо пропорциональна силе
нормального давления:
1. Сила трения скольжения прямо пропорциональна силе
нормального давления: ![]()
где R-сила нормального давления, направлена перпендикулярно опорной поверхности; f- коэффициент трения скольжения.
Рисунок 3.3.
В
случае движения тела по наклонной плоскости (рисунок 3.3)
![]()
α – угол наклона плоскости к горизонту.
Сила трения всегда направлена в сторону, обратную направлению движения.
2. Сила трения меняется от нуля до некоторого максимального значения, называемого силой трения покоя (статическое трение):
![]()
Ff0 – статическая сила трения (сила трения покоя).
3. Сила трения при движении меньше силы трения покоя. Сила трения при движении называется динамической силой трения (Ff):
![]()
Поскольку
сила нормального давления, зависящая от веса и направления опорной поверхности,
не меняется, то различают статический и динамический коэффициенты трения: ![]()
![]()
Коэффициент трения скольжения зависит от следующих факторов:
- от материала
-от наличия смазки
-от скорости взаимного перемещения
Трение качения
 Сопротивление
при качении связано с взаимной деформацией грунта и колеса и значительно меньше
трения скольжения.
Сопротивление
при качении связано с взаимной деформацией грунта и колеса и значительно меньше
трения скольжения.
Для равномерного качения колеса необходимо прикладывать силу Fдв (рисунок 3.4)
Условие качения колеса состоит в том, что движущийся момент должен быть не меньше момента сопротивления:
Рисунок 3.4.
![]() ; N=G;
; N=G; ![]()
где к- максимальное значение плеча принимается за коэффициент трения качения.
Работа и мощность
 Работа служит
мерой действия силы, работа – скалярная величина.
Работа служит
мерой действия силы, работа – скалярная величина.
![]()
Мощность – работа, выполненная в единицу времени.
Рисунок 3.5.
![]()
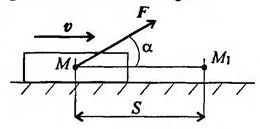
Мощность при поступательном движении

![]()
Рисунок 3.6.
Средняя
мощность при поступательном движении равна произведению модуля силы на среднюю
скорость перемещения и на косинус угла между направлениями силы и скорости.
3.2.Примеры решения практических задач
Пример
1: Свободная
материальная точка, масса которой 5 кг, движется согласно уравнению ![]() . Определить величину движущей
силы.
. Определить величину движущей
силы.
Решение:
1.
Ускорение точки:![]()
2. Действующая сила согласно основному закону динамики F=ma; F=5*0,96=4,8H
Пример 2: К двум материальным точкам массой m1=2кг и m2= 5 кг приложены одинаковые силы. Сравните величины ускоренней.
Решение:
Согласно
третей аксиоме динамики ускорения обратно пропорциональны массам: ![]()
 Пример
3:
Определите работу силы тяжести при перемещении груза из точки А в точку С по
наклонной плоскости (рисунок 3. 7). Сила тяжести тела 1500Н. АВ= 6 м, ВС=4м.
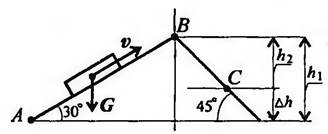
Пример
3:
Определите работу силы тяжести при перемещении груза из точки А в точку С по
наклонной плоскости (рисунок 3. 7). Сила тяжести тела 1500Н. АВ= 6 м, ВС=4м.
Решение:
Рисунок 3.7.
1.
Работа силы тяжести зависит только от изменения высоты груза. Изменение высоты
при перемещении из точки А в точку С :
![]()
![]()
![]()
2. Работа силы тяжести:
![]()
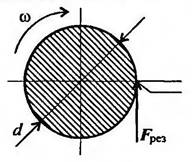 Пример
3: Определите
работу силы резания за 3 мин. Скорость вращения детали 120 об/мин, диаметр
обрабатываемой детали 40мм, сила резания 1кН. (рисунок 3.8)
Пример
3: Определите
работу силы резания за 3 мин. Скорость вращения детали 120 об/мин, диаметр
обрабатываемой детали 40мм, сила резания 1кН. (рисунок 3.8)
Решение:
1. Работа при вращательном движении:
![]()
2. Угловая частота вращения 120 об/мин
Рисунок 3.8.
3.
Число оборотов за заданное время составляет z=120*3=360
об.
Угол поворота за это время φ=2πz=2*3,14*360=2261рад
4. Работа за 3 оборота: W=1*0,02*2261=45,2 кДж
Список литературы
1. Олофинская, В.П. « Техническая механика», Москва «Форум»2011г.
2. Эрдеди А.А. Эрдеди Н.А. Теоретическая механика. Сопротивление материалов.- Р-н-Д; Феникс, 2010
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.