
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Иркутский государственный университет»
(ФГБОУ ВО «ИГУ»)
Педагогический институт
Кафедра математики и методики обучения математике
Направление подготовки: 44.03.05
Педагогическое образование
(с двумя профилями подготовки)
Профиль: Математика-Информатика
Форма обучения: заочная
Гальянова Ольга Викторовна
СЕРИЯ ЗАДАЧ С ПАРАМЕТРАМИ ИЗ СОДЕРЖАНИЯ ОГЭ
Курсовая работа бакалавра
Студент _________О.В. Гальянова Руководитель:
ст. преподаватель кафедры
МиМОМ ПИ ИГУ,
Курьякова Татьяна Сергеевна
Нормоконтролёр: зав. кафедрой
к.ф.-м.н., доцент _______ З.А. Дулатова
Работа защищена «__»______2017 г.
с оценкой_______________________
Протокол №_________
Иркутск 2017
СОДЕРЖАНИЕ
|
Введение |
3 |
|
Глава 1. Теоретические основы решения задач с параметрами |
3 |
|
1.1. Понятие параметра и сводящимся к его вычислению заданиям |
4 |
|
1.2. Анализ заданий с параметрами из содержания учебников алгебры 7-9 классов |
5 |
|
1.3. Типы задач с параметрами из содержания ОГЭ |
10 |
|
|
|
|
Глава 2. Примеры заданий с параметрами из содержания ОГЭ |
12 |
|
2.1. Задания, в которых нахождение параметра связано с анализом расположения некоторой прямой относительно заданного графика функции |
12 |
|
2.1.1. Задания, в которых указывается конкретное количество общих точек графиков (или их отсутствие) |
12 |
|
2.1.2. Задания, в которых указывается наибольшее (наименьшее) количество общих точек |
28 |
|
2.2. Задания, в которых нахождение параметра осуществляется аналитически |
28 |
|
|
|
|
Заключение |
31 |
|
Список литературы |
33 |
Введение
Исходя из анализа определений параметра в толковых словарях разных авторов, можно сделать вывод, что параметр в нашей жизни, это то, что позволяет отличить сравнительно однородные предметы, процессы и явления друг от друга. Так, по таким параметрам как температура, давление и частота сокращения сердечной мышцы, можно отличить больного человека от здорового; бытовые приборы из семейства кухонных комбайнов, отличаются по таким параметрам, как мощность, функциональность и т.п. То есть анализируя определенные количественные характеристики (параметры) того или иного предмета, процесса или явления, приходят к качественным выводам (например, «здоров» или «не здоров»). Так, если перевести на математический язык, решая задания с параметром, мы приходим к тем качественным выводам, которые могут быть в том или ином процессе или явлении (при решении уравнений с параметрами эти выводы связаны с ответом на вопрос о наличии или отсутствии решения, а при наличии решения - о количестве корней). Следовательно, сложно переоценить важность смысловой составляющей заданий с параметром для нашей жизни.
Задачи с параметрами, вводимые в школьном курсе математики содействуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков решения других задач. Они обладают диагностической ценностью, так как с помощью их можно проверить знания основных разделов математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности и перспективные возможности успешного овладения курса математики в высших учебных заведениях.
Актуальность данной темы связана и с тем, что задания с параметром встречаются при сдаче итоговых выпускных экзаменах по математике в школе, хотя на изучение данной темы в школьной программе времени практически не уделяется (в рабочих программах не для математических классов задания с параметрами не предусмотрены), в основном данная тема выносится на факультативные (или иные дополнительные) занятия. Из анализа основных учебников школьной программы до 10-11 классов становится понятным, что задания с параметрами встречаются только у авторов учебников с углубленным уровнем изучения математики. Во время сбора информации по данной теме, нами были проанализированы учебники по алгебре 7,8 и 9 классов следующих авторов: Ю.Н. Макарычева, Г.К. Муравина, Ш.А. Алимова, А.Г. Мордковича, С.М. Никольского, Г.В. Дорофеева, Л.Г. Петерсон, Н.Я. Виленкина, Ю.М. Колягина. В учебниках 7 класса акцент на существование заданий с параметрами не делается. В 8 классе задания с параметрами встречаются в учебниках углубленного уровня, таких авторов, как А.Г. Мордкович [2, с.229] и Н.Я. Виленкин [1, с.244]. В 9 классе – в учебниках с углубленным уровнем, таких авторов, как Ю.Н. Макарычев [4, с.109], Г.В. Дорофеев [3, с.177], А.Г. Мордкович [5, с.51].
Кроме того, материал по данной теме представляется в рамках параграфа в разделах с уравнениями или неравенствами, то есть в сравнительно сжатом виде. В связи с чем, задания с параметром вызывают некоторую сложность для уяснения учащимися. Возможно, это связано с тем, что при решении заданий с параметрами затрагиваются знания по основным фундаментальным линиям практически всего школьного курса математики (функциональная линия, линия уравнений и неравенств, линия числа, линия тождественных преобразований).
Итак, ограниченный объем теоретического и практического материала по теме с одной стороны, и наличие заданий с параметром в КИМах для школьников 9 класса – с другой, обусловило написание данной курсовой работы, целью которой является анализ основных типов заданий, встречающихся на экзамене в 9 классе, попытка разработать общее предписание для решения этих заданий и на конкретных примерах его реализовать.
Все вышесказанное определяет актуальность выбранной мною темы.
Объект исследования: теоретические основы решения заданий с параметром.
Предмет исследования: серия заданий с параметром, встречающихся на итоговой аттестации по математике в 9 классе.
Цель работы: выделить основные типы заданий, в условии которых указывается необходимость построения графиков, сформулировать предписание, необходимое для решения данных заданий, продемонстрировать его применение при решении заданий с параметрами основного курса алгебры.
Цель реализуется через решение следующих задач:
1) определить понятие параметра и уравнения с параметром;
2) составить предписание использования графического метода при решении заданий с параметром;
3) определить типы заданий с параметром;
4) описать решения задач с параметрами основной школы.
Структура и объем работы: работа состоит из введения, двух глав, заключения, списка литературы.
В первой главе рассмотрены теоретические основы решения заданий с параметром в школьном курсе математики, а также представлен анализ основных учебников 7,8,9 классов поданной теме и схема основных типов заданий.
Вторая глава посвящена обучению решения основных типов заданий с параметром, в условии которых указывается необходимость построения графиков.
Глава 1. Теоретические основы решения задач с параметрами
В главе описаны теоретические основы решения задач с параметрами, изложен анализ учебников основной школы, выделены типы заданий с параметрами, описано предписание по решению заданий с параметрами.
1.1. Понятие параметра и сводящимся к его вычислению заданиям
Существуют различные определения параметра. В частности, в толковых словарях параметр трактуется как:
1) как величина, характеризующая какое-нибудь основное свойство машины, устройства, системы или явления (словарь Ожегова С.И., Шведовой Н.Ю и др.) [10];
2) математическая величина (гр. parametron – отмеривающий), входящая в формулы и выражения, значение которой является постоянным в пределах рассматриваемой задачи (величина, показатель, характеризующий какое-либо свойство устройства, процесса, вещества) (энциклопедический словарь) [10];
3) это величина (от греч. меряю, сопоставляю), входящая в математическую формулу и сохраняющая постоянное значение в пределах одного явления или для данной частной задачи, но при переходе к другому явлению, к другой задаче меняющая свое значение (Д.Н.Ушаков) [10].
При анализе различных сайтов, содержащих информацию о заданиях с параметрами, а также учебных пособий, направленных на обучение решению этих же заданий, следует отметить, что теоретический материал сводится в основном к ответам на такие вопросы: что такое уравнение (неравенство) с параметром; что значит решить уравнение (неравенство) с параметром.
Некоторые из этих теоретических выкладок следует привести для примера.
Уравнение (неравенство) с параметрами – математическое уравнение (неравенство), внешний вид и решение которого зависит от значения одного или нескольких параметров (Википедия) [11].
Решить уравнение с параметром, означает:
1.Найти все системы значений параметров, при которых данное уравнение имеет решение.
2.Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.(Википедия) [11]
Рассмотрим
уравнение ![]() где
где ![]() - переменные величины.
- переменные величины.
Любая система значений переменных ![]() при которой левая и
правая части этого уравнения принимают действительные значения, называется
системой допустимых значений переменных
при которой левая и
правая части этого уравнения принимают действительные значения, называется
системой допустимых значений переменных ![]() .
Пусть A- множество всех допустимых значений a, B – множество всех допустимых значений b и т.д. X
– множество всех допустимых значений x , то есть
.
Пусть A- множество всех допустимых значений a, B – множество всех допустимых значений b и т.д. X
– множество всех допустимых значений x , то есть ![]() Если из
каждого из множеств
Если из
каждого из множеств ![]() выбрать и зафиксировать
соответственно по одному значению
выбрать и зафиксировать
соответственно по одному значению ![]() и подставить их
в уравнение
и подставить их
в уравнение ![]() то
получим уравнение относительно x, то есть уравнение с одним неизвестным.
то
получим уравнение относительно x, то есть уравнение с одним неизвестным.
Решение
его зависит от выбранной нами системы значений ![]() и
будет иметь определенное числовое значение при каждом таком выборе,
следовательно решение уравнения
и
будет иметь определенное числовое значение при каждом таком выборе,
следовательно решение уравнения ![]() относительно x является функцией от
относительно x является функцией от ![]() . Если обозначить это решение через
. Если обозначить это решение через
![]() , то получим
, то получим ![]() .
.
Переменные ![]() ,
которые при решении уравнения считаются постоянными, называются параметрами, а
само уравнение, называется уравнением, содержащим параметры.
,
которые при решении уравнения считаются постоянными, называются параметрами, а
само уравнение, называется уравнением, содержащим параметры.
Решить уравнение ![]() - значит указать, при
каких значениях параметров существуют решения и каковы они.
- значит указать, при
каких значениях параметров существуют решения и каковы они.
В процессе решения уравнений, существенную роль играют теоремы о равносильности. Два уравнения, содержащие одни и те же параметры, называются равносильными, если:
а) они имеют смысл при одних и тех же значениях параметров;
б) каждое решение первого уравнения, является решением второго и наоборот. (Г.А. Ястребинский [9, с.12]).
1.2. Анализ заданий с параметрами из содержания учебников алгебры 7-9 классов
Проанализировав некоторые задания с параметром, можно сделать вывод, что большая их часть сводится к решению уравнений и неравенств различных уровней сложности. Поэтому теоретический материал учебников школьного курса математики связан с описанием таких понятий, как уравнение с параметром, что значит решить уравнение с параметром, при чем понятия в основном вводятся через приведение примеров и описание.
Считаю необходимым привести примеры определения основных понятий, связанных с решением уравнений с параметрами.
Уравнения с параметрами – это уравнения, в которых в роли коэффициентов выступают не конкретные числа, а буквенные выражения (Мордкович А.Г.- 8 кл.) [2, с.229].
Параметры – это буквы, которыми заданы некоторые коэффициенты в уравнениях, следовательно, данные уравнения – это уравнения с параметром. (Виленкин Н.Я.- 8 кл.) [1, с.244].
Уравнение с параметром – это уравнение, в котором есть буквенные коэффициенты. (Дорофеев Г.В.- 9 кл.) [3, с.177]..
Макарычев приводит пример решения линейного уравнения, предлагая разные числа в качестве коэффициентов и показывая, что в связи с изменением значения коэффициента изменяется и окончательный результат. После чего вводит понятие параметр приравнивая его коэффициенту, наличие которого дает основание говорить, что это уравнение с параметром.
Решить уравнение с параметром:
– исследовать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметра;
– найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения. (Виленкин Н.Я. – 8 кл.) [1, с.244].
Решить уравнение с параметром – это значит установить соответствие, позволяющее для любого значения параметра найти соответствующее множество корней (Макарычев Ю.Н. – 9 кл.) [4, с.109]. Ю.Н. Макарычев выделяет два вида уравнений с параметром: целые и дробно-рациональные.
Для целей данной работы необходимо ввести еще одно понятие – особое или контрольное значение параметра, называется такое значение, при котором обращается в нуль коэффициент при неизвестном.
Хотелось бы остановиться на таком вопросе, чем отличается параметр в уравнении, от самой неизвестной в этом же уравнении. Ответ на данный вопрос должен внести ясность в понимание сути данных заданий.
Так, при нахождении значения переменной (неизвестной) в уравнении мы отвечаем на вопрос «Чему равен корень данного уравнения, то есть находили число, превращающее наше уравнение в верное равенство». При нахождении значения параметра, мы отвечаем на вопрос, «имеет ли уравнение корни при определенном значении параметра, если да, то каково их количество».
Задачи с параметром можно условно разделить на два типа:
– для всех значений параметра найти решение (если хотя бы один случай остался не исследованным, признать такое решение удовлетворительным нельзя);
– указать возможные значения параметра, при которых уравнение обладает определенными свойствами (например, имеет одно решение, не имеет решение, решение принадлежит промежутку).
В школьном курсе математики решение уравнений осуществляется как аналитическим способом, так и графическим, то есть при помощи построения графиков. Данный способ актуален при решении сложных уравнений, содержащих выражения разных классов. Так вот задания с параметром, выносимые на государственную итоговую аттестацию в 9 классе по смыслу вытекают из графического метода и относится ко второму вышеуказанному типу, то есть связано с нахождением значения параметра, при котором уравнение обладает определенными свойствами.
1.3. Основные типы заданий с параметром, выносимые на итоговую государственную аттестацию в 9 классе
Как показал анализ заданий из содержания пробных и тренировочных вариантов ОГЭ, их можно классифицировать различными способами:
1) по способу решения – задания с параметрами делятся на те, которые решаются аналитически и те, решение которых рациональнее осуществлять графически;
2) по требованию задания – на построение графиков, на решение уравнений или неравенств;
3) по виду входящих в задание выражений – задачи, связанные с модулями и без них, задачи, связанные с кусочно-заданными функциями и с функциями, заданными одной формулой и пр.
Следуя цели исследования, нами мы посчитали типизировать задачи с параметрами следующим образом (см. схему.):
Мы сочли возможным составить общее предписание к решению заданий с параметрами, связанными с построением графиков:
1. Выясняем тип задания (для решения вопроса о применении конкретного способа или алгоритма решения).
2. Находим область определения заданных функций.
3. Производим упрощение исходной формулы при помощи тождественных преобразований (при необходимости).
4. Строим график заданной функции (без параметра).
5. Проводим анализ расположения функции с параметром относительно первого графика, особое внимание уделяем точкам разрыва, экстремумам функции).
 6. Составление ответа.
6. Составление ответа.
В следующей главе нами будет продемонстрировано применение предписания для решения различных заданий с параметрами основной школы.
Глава 2. Примеры заданий с параметрами из содержания ОГЭ,
связанные с построением графиков
В главе описаны решения заданий, приведены примеры заданий разных типов, реализованы теоретические предписания, описанные в теоретической части работы.
2.1. Задания, в которых нахождение параметра связано с анализом расположения некоторой прямой относительно заданного графика функции
Среди заданий данного направления следует выделить два основных типа:
– задания, в которых указывается конкретное количество общих точек графиков функций (или их отсутствие);
– задания, связанные с построением графиков с заданным параметром, отвечающим конкретным условиям задачи.
Разберем решение каждого из указанного подвидов заданий на конкретных примерах.
2.1.1.Задания, в которых указывается конкретное количество общих точек
графиков функций (или их отсутствие)
Так как заданий данного типа наибольшее количество, при анализе их решения считаем необходимым выделить и показать основные случаи:
– задания, связанные с упрощением исходной формулы;
– задания, отличающиеся по типу прямой, с которой нужно найти пересечение;
– задания, отличающиеся по виду ответа.
а) Задания, связанные с упрощением исходной формулы
Рассмотрим примеры, в которых упрощение исходной формулы требуется и примеры, в которых данных преобразований не требуется.
В первом примере потребуется упрощение аналитического задания исходной функции.
Пример
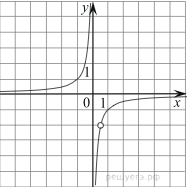
1. Постройте график функции ![]() и определите, при каких значениях
k прямая
и определите, при каких значениях
k прямая ![]() имеет с графиком ровно одну общую
точку.
имеет с графиком ровно одну общую
точку.
 Решение: Найдем Df
исходной функции
Решение: Найдем Df
исходной функции ![]() :
:
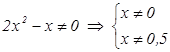 .
.
Упрощаем аналитическое задание функции: ![]() .
.
Строим график функции ![]() , (см. рис.).
, (см. рис.).
Проводим анализ расположения прямой –
графика функции ![]() относительно
построенного графика.
относительно
построенного графика.
Определяем график прямой: графиком функции
![]() является
прямая, проходящая через начало координат.
является
прямая, проходящая через начало координат.
Изменение параметра k данного графика при водит его к изменению угла наклона, а в случае k = 0, график функции совпадает с осью Ox (других вариантов нет).
Начинаем рассуждать:
- при k > 0 прямая располагается в 1 и 3 координатном углах, где не будет иметь точек пересечения со вторым графиком;
- при k = 0 график функции совпадая с осью также не будет иметь со вторым графиком ни одной общей точки;
- при k < 0 прямая будет располагаться во 2 и 4
координатных углах, и следовательно иметь 2 общие точки со вторым графиком.
Однако, учитывая область определения первой функции в точке 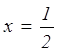 , график имеет
разрыв, и прямая, проходя через этот разрыв будет иметь с первым графиком ровно
одну общую точку.
, график имеет
разрыв, и прямая, проходя через этот разрыв будет иметь с первым графиком ровно
одну общую точку.
а) Найдем координату по оси Oy в данной точке, подставив в функцию 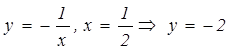 .
.
б)
подставим в функцию соответствующие значения y
и x и найдем значение ![]() .
.
Ответ: ![]() .
.
Во втором примере также потребуется упрощение аналитического задания исходной функции.
Пример
2. Постройте график функции 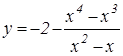 и определите, при каких значениях
m прямая
и определите, при каких значениях
m прямая ![]() имеет с графиком ровно две общие
точки.
имеет с графиком ровно две общие
точки.
 Решение: найдем Df
исходной функции:
Решение: найдем Df
исходной функции: 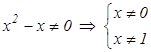 .
.
Упрощаем аналитическое задание функции: 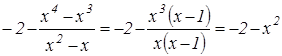 .
.
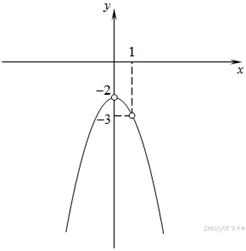
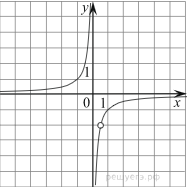
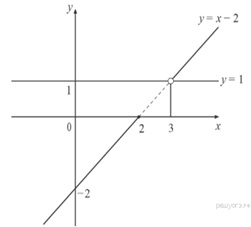
Строим график функции ![]() (см. рис.).
(см. рис.).
Проводим анализ расположения прямой –
графика функции ![]() относительно
построенного графика.
относительно
построенного графика.
Определяем график прямой:
Графиком функции ![]() является
прямая, параллельная оси Ох.
является
прямая, параллельная оси Ох.
Изменение параметра m данного графика приводит к его «движению» вдоль оси Оy (других вариантов нет).
При «движении» данной прямой вдоль оси Оу, можно выделить следующие моменты:
- при ![]() прямая с графиков функции не
имеет общих точек;
прямая с графиков функции не
имеет общих точек;
- при ![]() – прямая имеет с графиком
одну общую точку;
– прямая имеет с графиком
одну общую точку;
- при ![]()
![]() –
прямая с графиком будет иметь две точки, однако с учетом области определения,
в точке
–
прямая с графиком будет иметь две точки, однако с учетом области определения,
в точке ![]() , прямая
с графиком параболы будет иметь также одну точку, следовательно данную точку
следует исключить.
, прямая
с графиком параболы будет иметь также одну точку, следовательно данную точку
следует исключить.
Ответ: ![]() .
.
Во третьем
примере упрощение аналитического задания исходной функции связано с применением
формулы ![]() и формулы разложения на множители
квадратного трехчлена.
и формулы разложения на множители
квадратного трехчлена.
 Пример
3. Постройте график функции
Пример
3. Постройте график функции 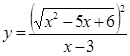 и найдите все значения m при которых прямая
и найдите все значения m при которых прямая ![]() не имеет с графиком данной функции
общих точек.
не имеет с графиком данной функции
общих точек.
Решение: найдем Df исходной функции 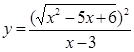 :
:
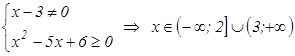 .
.
Упрощаем аналитическое задание функции: 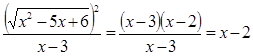 . Строим график
функции
. Строим график
функции ![]() на области
определения (см. рис.).
на области
определения (см. рис.).
Проводим анализ расположения прямой
– графика функции ![]() относительно
построенного графика.
относительно
построенного графика.
Определяем график прямой: Графиком
функции ![]() является
прямая, параллельная оси Ох.
является
прямая, параллельная оси Ох.
Изменение параметра m данного графика приводит к его «движению» вдоль оси Оy. (Других вариантов нет).
Начинаем двигаться вдоль оси Оy сверху вниз, и видим, что:
- при ![]() прямая с графиков функции имеет
одну общую точку;
прямая с графиков функции имеет
одну общую точку;
- при ![]() – прямая не имеет с
графиком общих точек.
– прямая не имеет с
графиком общих точек.
Ответ: ![]() .
.
б) Задания, в которых не требуется упрощение исходной формулы
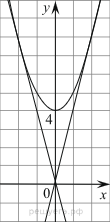 Пример 4. Найдите
все значения k, при каждом из которых прямая
Пример 4. Найдите
все значения k, при каждом из которых прямая ![]() имеет
с графиком функции
имеет
с графиком функции ![]() ровно одну общую точку.
Постройте этот график и все такие прямые.
ровно одну общую точку.
Постройте этот график и все такие прямые.
Решение: найдем Df исходной функции: ![]() .
.
Находим точки пересечения графиков функций ![]() и
и ![]() :
: ![]()
![]()
При ![]() , координаты общих точек
равны
, координаты общих точек
равны ![]() ; при
; при ![]() , координаты общих точек равны
, координаты общих точек равны![]() .
.
Ответ: ![]() .
.
Задания, отличающиеся по типу прямой, с которой нужно найти пересечение
а) тип прямой: ![]() .
.
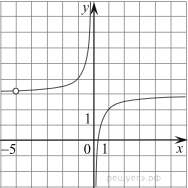 Пример 5.
Постройте график функции
Пример 5.
Постройте график функции ![]() и определите,
при каких значениях k прямая
и определите,
при каких значениях k прямая ![]() не имеет с графиком ни одной общей
точки.
не имеет с графиком ни одной общей
точки.
Решение: найдем Df исходной функции: 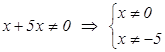 .
.
Упрощаем аналитическое задание функции: 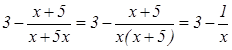 .
.
Строим график функции ![]() (см. рис.).
(см. рис.).
Определяем график прямой: графиком функции
![]() является
прямая, параллельная оси Ох. Изменение параметра k данного графика приводит
к его «движению» вдоль оси Оy.
является
прямая, параллельная оси Ох. Изменение параметра k данного графика приводит
к его «движению» вдоль оси Оy.
При «движении» данной прямой вдоль оси Оу, можно выделить следующие моменты:
- при ![]() прямая с графиком функции имеет
одну общую точку;
прямая с графиком функции имеет
одну общую точку;
- при ![]() – прямая не имеет с графиком
функции общих точек;
– прямая не имеет с графиком
функции общих точек;
- замечаем, что в точке ![]() график функции имеет разрыв.
Найдем значение y в данной точке:
график функции имеет разрыв.
Найдем значение y в данной точке: ![]() .
.
Ответ: ![]() .
.
б) тип прямой: ![]() .
Задания с указанным типом прямой рассмотрены в примерах № 1 и № 4.
.
Задания с указанным типом прямой рассмотрены в примерах № 1 и № 4.
Задания, отличающиеся по виду ответа
а) ответ в виде числового промежутка
 Пример
6. Постройте график функции
Пример
6. Постройте график функции 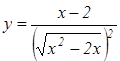 и определите, при каких значениях
k прямая
и определите, при каких значениях
k прямая ![]() имеет с графиком ровно одну общую
точку.
имеет с графиком ровно одну общую
точку.
Решение: Найдем Df исходной функции: ![]() .
.
Упрощаем аналитическое задание функции: 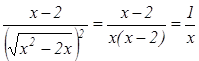 .
.
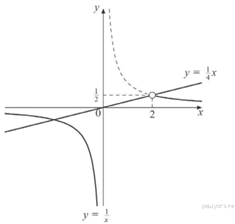
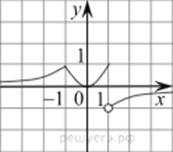
Строим график функции ![]() (см. рис.).
(см. рис.).
Проводим анализ расположения прямой
– графика функции ![]() относительно
построенного графика. Определяем график прямой: графиком функции
относительно
построенного графика. Определяем график прямой: графиком функции ![]() является прямая,
проходящая через начало координат.
является прямая,
проходящая через начало координат.
Изменение параметра k данного графика при водит его к изменению угла наклона, а в случае k = 0, график функции совпадает с осью Ox.
Начинаем рассуждать:
- при k < 0, прямая располагается в 2 и 4 координатном углах, где не будет иметь точек пересечения со вторым графиком;
- при k = 0 график функции совпадая с осью также не будет иметь со вторым графиком ни одной общей точки;
- при k > 0 прямая будет располагаться во 1 и 3
координатных углах, и следовательно иметь 2 общие точки со вторым графиком.
Однако, учитывая область определения первой функции на промежутке ![]() ее график не существует,
следовательно прямая
ее график не существует,
следовательно прямая ![]() , расположенная в
данном промежутке будет иметь с графиком функции только одну общую точку.
, расположенная в
данном промежутке будет иметь с графиком функции только одну общую точку.
Найдем
коэффициент прямой ![]() в точке
в точке ![]() :
:
а) Найдем координату по оси Oy в данной точке, подставив в функцию ![]() ;
;
б)
подставим в функцию соответствующие значения y
и x и найдем значение 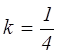 .
.
Заметим, что при «движении» прямой к оси Оу, значение коэффициента будет увеличиваться до бесконечности.
Ответ: 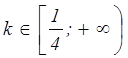 .
.
 Пример 7.
Постройте график функции
Пример 7.
Постройте график функции 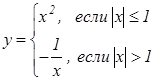 и определите,
при каких значениях k прямая
и определите,
при каких значениях k прямая ![]() имеет с графиком ровно одну общую
точку.
имеет с графиком ровно одну общую
точку.
Решение: Найдем Df исходной функции: ![]() .
.
Строим график функции (см. рис.).
Проводим анализ расположения прямой – графика функции
![]() относительно
построенного графика.
относительно
построенного графика.
Определяем график прямой: графиком функции ![]() является прямая,
параллельная оси Ох.
является прямая,
параллельная оси Ох.
При «движении» данной прямой вдоль оси Оу, можно выделить следующие моменты:
- на промежутке![]() прямая с графиком
функции не имеет общих точек;
прямая с графиком
функции не имеет общих точек;
- на промежутке ![]() прямая имеет с графиком
функции три общих точки;
прямая имеет с графиком
функции три общих точки;
- на
промежутке ![]() прямая имеет с
графиком функции одну общую точку;
прямая имеет с
графиком функции одну общую точку;
- на промежутке![]() прямая с графиком
функции не имеет общих точек.
прямая с графиком
функции не имеет общих точек.
Ответ: ![]() .
.
б) ответ в виде отдельных чисел
Пример
8. Постройте график функции ![]() и определите, при каких значениях
m прямая
и определите, при каких значениях
m прямая ![]() имеет с графиком ровно одну общую
точку.
имеет с графиком ровно одну общую
точку.
Решение: Найдем Df исходной функции ![]() :
: ![]() .
.
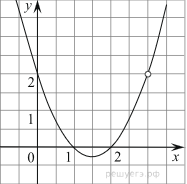 Упрощаем
аналитическое задание функции:
Упрощаем
аналитическое задание функции: ![]() .
.
Строим график функции ![]() (см. рис.).
(см. рис.).
Проводим анализ расположения прямой –
графика функции ![]() относительно
построенного графика.
относительно
построенного графика.
Определяем график прямой: графиком функции
![]() является
прямая, параллельная оси Ох.
является
прямая, параллельная оси Ох.
Изменение параметра m данного графика приводит к его «движению» вдоль оси Оy. (Других вариантов нет).
При «движении» данной прямой вдоль оси Оу, можно выделить следующие моменты:
- при 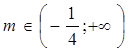 прямая с графиком функции
имеет две общие точки ;
прямая с графиком функции
имеет две общие точки ;
- при 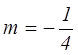 – прямая имеет с графиком
одну общую точку;
– прямая имеет с графиком
одну общую точку;
- при 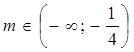 – прямая не имеет с графиком
ни одной общей точки.
– прямая не имеет с графиком
ни одной общей точки.
Заметим, что с учетом области
определения в точке ![]() график
параболы прерывается, следовательно прямая
график
параболы прерывается, следовательно прямая ![]() ,
проходя через данную точку имеет с параболой также одну общую точку.
,
проходя через данную точку имеет с параболой также одну общую точку.
Найдем
ординату данной точки, подставив в функцию ![]() .
.
Ответ: ![]() .
. ![]()
Пример
9. Постройте график функции 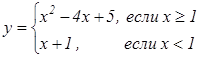 и определите, при каких значениях
k прямая
и определите, при каких значениях
k прямая ![]() имеет с графиком ровно две общие точки.
имеет с графиком ровно две общие точки.
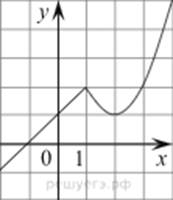 Решение: Найдем Df
исходной функции:
Решение: Найдем Df
исходной функции: ![]() .
.
Строим график функции (см. рис.).
Проводим анализ расположения прямой – графика функции
![]() относительно
построенного графика.
относительно
построенного графика.
Определяем график прямой: графиком функции ![]() является прямая,
параллельная оси Ох.
является прямая,
параллельная оси Ох.
При «движении» данной прямой вдоль оси Оу можно выделить следующие моменты:
- на промежутке![]() прямая с графиком функции имеет
одну общую точку;
прямая с графиком функции имеет
одну общую точку;
- на промежутке ![]() прямая имеет с графиком
функции три общих точки;
прямая имеет с графиком
функции три общих точки;
- в
точках ![]() и
и ![]() прямая
имеет с графиком функции две общих точки.
прямая
имеет с графиком функции две общих точки.
Ответ: ![]()
Задания, отличающиеся по количеству общих точек
а) задано определенное количество общих точек
Пример
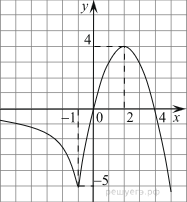
10. Постройте график функции 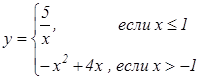 и определите, при каких значениях
k прямая
и определите, при каких значениях
k прямая ![]() будет пересекать построенный
график в трех точках.
будет пересекать построенный
график в трех точках.
Решение: найдем Df исходной функции: ![]() .
.
Строим график функции (см. рис.).
 Проводим анализ
расположения прямой – графика функции
Проводим анализ
расположения прямой – графика функции ![]() относительно построенного графика.
относительно построенного графика.
Определяем график прямой: графиком функции ![]() является прямая,
параллельная оси Ох.
является прямая,
параллельная оси Ох.
При «движении» данной прямой вдоль оси Оу, можно выделить следующие моменты:
- на промежутке![]() прямая с графиком
функции имеет одну общую точку;
прямая с графиком
функции имеет одну общую точку;
- в точке
![]() и на промежутке
и на промежутке ![]() прямая имеет с графиком две общие
точки;
прямая имеет с графиком две общие
точки;
- на промежутке ![]() прямая имеет с графиком
функции три общих точки;
прямая имеет с графиком
функции три общих точки;
- в точке
![]() прямая имеет с графиком одну общую
точку;
прямая имеет с графиком одну общую
точку;
- на промежутке![]() прямая с графиком
функции не имеет общих точек.
прямая с графиком
функции не имеет общих точек.
Ответ: ![]() .
.
б) задано количество общих точек через союз “или”
 Пример 11.
Постройте график функции
Пример 11.
Постройте график функции 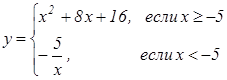 и определите,
при каких значениях k прямая
и определите,
при каких значениях k прямая ![]() имеет с графиком одну или две
общие точки.
имеет с графиком одну или две
общие точки.
Решение: найдем Df исходной функции: ![]() .
.
Строим график функции (см. рис.).
Проводим анализ расположения прямой – графика функции
![]() относительно
построенного графика.
относительно
построенного графика.
Определяем график прямой: графиком функции ![]() является прямая,
параллельная оси Ох.
является прямая,
параллельная оси Ох.
При «движении» данной прямой вдоль оси Оу, можно выделить следующие моменты:
- на промежутке![]() прямая с графиком
функции не имеет общих точек;
прямая с графиком
функции не имеет общих точек;
- в точке
![]() и на промежутке
и на промежутке ![]() прямая имеет с графиком одну общую
точку;
прямая имеет с графиком одну общую
точку;
- в точке
![]() прямая имеет с графиком 2 общие
точки;
прямая имеет с графиком 2 общие
точки;
- на промежутке ![]() прямая имеет с графиком
функции три общих точки;
прямая имеет с графиком
функции три общих точки;
- в точке
![]() прямая имеет с графиком одну общую
точку;
прямая имеет с графиком одну общую
точку;
- на промежутке![]() прямая с графиком
функции имеет три общие точки;
прямая с графиком
функции имеет три общие точки;
Выбираем нужный ответ.
Ответ: ![]() .
.
в) ни одной общей точки
Данный случай рассмотрен в примере № 5.
Функции, содержащие выражения под знаком модуля
При построении графиков функций, аналитическое задание которых содержит выражения, стоящие под знаком модуля, следует особое внимание уделять правилам раскрытия модуля, что придает данным заданиям некоторую особенность, в связи с чем примеры данных заданий выделены в отдельный раздел, в котором представлены примеры заданий, отличающиеся видом графика.
Пример
12. Постройте график функции ![]() и определите, при каких значениях
k прямая
и определите, при каких значениях
k прямая ![]() имеет с графиком ровно три общие
точки.
имеет с графиком ровно три общие
точки.
Решение: Найдем Df исходной функции ![]() :
: ![]() .
.
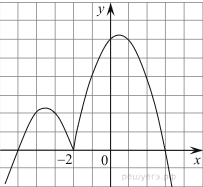 Раскрываем модуль и строим
график функции
Раскрываем модуль и строим
график функции 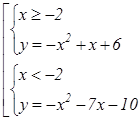 (см.
рис.).
(см.
рис.).
Проводим анализ расположения прямой – графика функции
![]() относительно
построенного графика. Определяем график прямой: Графиком функции
относительно
построенного графика. Определяем график прямой: Графиком функции ![]() является прямая,
параллельная оси Ох.
является прямая,
параллельная оси Ох.
При «движении» данной прямой вдоль оси Оу, можно выделить следующие моменты:
- на промежутке ![]() прямая не имеет с графиком
функции общих точек;
прямая не имеет с графиком
функции общих точек;
- в точке ![]() прямая имеет с графиком одну общую
точку;
прямая имеет с графиком одну общую
точку;
- на промежутке![]() прямая с графиком
функции имеет две общие точки;
прямая с графиком
функции имеет две общие точки;
- в точке
![]() прямая имеет с графиком функции
три общие точки;
прямая имеет с графиком функции
три общие точки;
- на промежутке ![]() прямая имеет с графиком
функции четыре общих точки.
прямая имеет с графиком
функции четыре общих точки.
Ответ: ![]() .
.
Пример
13. Постройте график функции 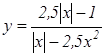 и определите, при каких значениях
k прямая
и определите, при каких значениях
k прямая ![]() не имеет с графиком общих точек.
не имеет с графиком общих точек.
Решение: Найдем Df исходной функции 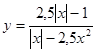 :
: ![]() .
.
Раскрываем модуль и строим график функции 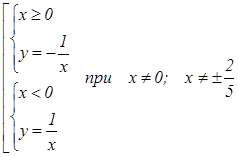 (см. рис.).
(см. рис.).
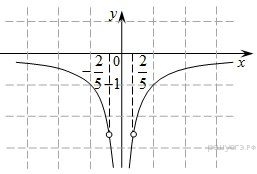 Проводим анализ расположения прямой
– графика функции
Проводим анализ расположения прямой
– графика функции ![]() относительно
построенного графика. Определяем график прямой: графиком функции
относительно
построенного графика. Определяем график прямой: графиком функции ![]() является прямая,
проходящая через начало координат.
является прямая,
проходящая через начало координат.
Изменение параметра k данного графика при водит его к изменению угла наклона, а в случае k = 0, график функции совпадает с осью Ox.
Начинаем рассуждать:
- при k
> 0, прямая располагается в 1 и 3 координатном углах, где имеет одну
общую точку с графиком. Замечаем, что учитывая область определения, функция в
точке 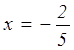 имеет
разрыв, и прямая, проходя через этот разрыв не будет иметь с первым графиком общих
точек.
имеет
разрыв, и прямая, проходя через этот разрыв не будет иметь с первым графиком общих
точек.
а) найдем координату по оси Oy в данной точке, подставив в функцию ![]() ;
;
б)
подставим в функцию соответствующие значения y
и x и найдем значение ![]() .
.
- при k = 0 график функции совпадая с осью также не будет иметь со вторым графиком ни одной общей точки.
- при k < 0 прямая будет располагаться во 2 и 4
координатных углах, и следовательно имеет одну общую точку с графиком. Замечаем,
что учитывая область определения, функция в точке 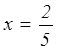 имеет разрыв, и прямая,
проходя через этот разрыв не будет иметь с первым графиком общих точек.
имеет разрыв, и прямая,
проходя через этот разрыв не будет иметь с первым графиком общих точек.
а) найдем координату по оси Oy в данной точке, подставив в функцию ![]() ;
;
б)
подставим в функцию соответствующие значения y и
x и найдем значение ![]() .
.
Ответ: ![]() .
.
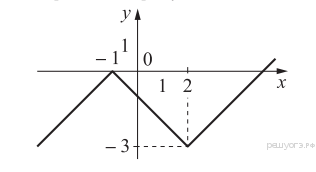 Пример
14. Постройте график функции
Пример
14. Постройте график функции ![]() и определите, при каких значениях
k прямая
и определите, при каких значениях
k прямая ![]() имеет с графиком ровно две общие
точки.
имеет с графиком ровно две общие
точки.
Решение: найдем Df исходной функции ![]() :
: ![]() .
.
Раскрываем модуль и строим график функции 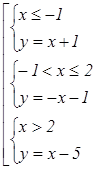 (см. рис.).
(см. рис.).
Проводим анализ расположения прямой –
графика функции ![]() относительно
построенного графика. Определяем график прямой: графиком функции
относительно
построенного графика. Определяем график прямой: графиком функции ![]() является прямая,
параллельная оси Ох. При «движении» данной прямой вдоль оси Оу,
можно выделить следующие моменты:
является прямая,
параллельная оси Ох. При «движении» данной прямой вдоль оси Оу,
можно выделить следующие моменты:
- на промежутке ![]() прямая имеет с графиком
функции одну общую точку;
прямая имеет с графиком
функции одну общую точку;
- в точке ![]() прямая имеет с графиком две общие
точки;
прямая имеет с графиком две общие
точки;
- на промежутке![]() прямая с графиком
функции имеет две общие точки;
прямая с графиком
функции имеет две общие точки;
- в точке
![]() прямая имеет с графиком функции
три общие точки.
прямая имеет с графиком функции
три общие точки.
Ответ: ![]() .
.
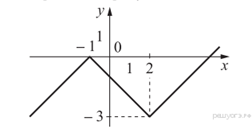 Пример
15. Постройте график функции
Пример
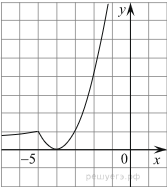
15. Постройте график функции 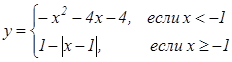 и определите, при каких значениях
k прямая
и определите, при каких значениях
k прямая ![]() имеет с графиком ровно две общие
точки.
имеет с графиком ровно две общие
точки.
Решение: найдем Df исходной функции: ![]() .
.
Раскрываем модуль и строим график функции 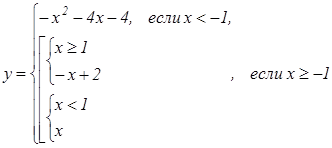 (см. рис.).
(см. рис.).
Проводим анализ расположения прямой
– графика функции ![]() относительно
построенного графика. Определяем график прямой: графиком функции
относительно
построенного графика. Определяем график прямой: графиком функции ![]() является прямая,
параллельная оси Ох. При «движении» данной прямой вдоль оси Оу,
можно выделить следующие моменты:
является прямая,
параллельная оси Ох. При «движении» данной прямой вдоль оси Оу,
можно выделить следующие моменты:
- на промежутке ![]() прямая не имеет с графиком
общих точек;
прямая не имеет с графиком
общих точек;
- в точке ![]() прямая имеет с графиком одну общую
точку;
прямая имеет с графиком одну общую
точку;
- на промежутке![]() прямая с графиком
функции имеет две общие точки;
прямая с графиком
функции имеет две общие точки;
- в точке
![]() прямая имеет с графиком функции
три общие точки;
прямая имеет с графиком функции
три общие точки;
- на промежутке![]() прямая с графиком функции
имеет четыре общие точки.
прямая с графиком функции
имеет четыре общие точки.
Ответ: ![]() .
.
2.1.2. Задания, в которых указывается наибольшее (наименьшее) количество общих точек
Данный тип заданий является частным случаем вышерассмотренных примеров. Его особенностью является то, что прямая, с которой необходимо искать точки пересечения задана не аналитически и при выборе нужного ответа, добавляется шаг, направленный на сравнение полученного результата.
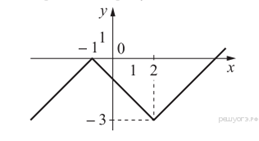 Пример
16. Постройте график функции
Пример
16. Постройте график функции ![]() . Какое наибольшее количество
общих точек график данной функции может иметь с прямой, параллельной оси
абсцисс?
. Какое наибольшее количество
общих точек график данной функции может иметь с прямой, параллельной оси
абсцисс?
Решение: Найдем Df исходной функции: ![]() .
.
Строим график данной функции. (см. рис.).
Замечаем, что прямая, параллельная оси абсцисс имеет
вид ![]() .
.
При «движении» данной прямой вдоль оси Оу, можно выделить следующие моменты:
- на промежутке ![]() прямая не имеет с графиком
общих точек;
прямая не имеет с графиком
общих точек;
- в точке ![]() прямая имеет с графиком две общие
точки;
прямая имеет с графиком две общие
точки;
- на промежутке![]() прямая с графиком
функции имеет четыре общие точки;
прямая с графиком
функции имеет четыре общие точки;
- в точке
![]() прямая имеет с графиком функции
три общие точки;
прямая имеет с графиком функции
три общие точки;
- на промежутке![]() прямая с графиком
функции имеет две общие точки.
прямая с графиком
функции имеет две общие точки.
Ответ: 4.
2.2. Задания, в которых нахождение параметра осуществляется аналитически
Отличие данных типов заданий с предыдущими, заключается в том, что при их решении необходимы некоторые аналитические вычисления, проводимые перед построением графика функций, а само построение графиков и нахождение координат точки их пересечения является целью данной задачи. В предыдущем же разделе 2.1 построенный график служил средством для достижения правильного решения.
Пример
17. Известно, что графики функции ![]() и
и ![]() имеют
ровно одну общую точку. Определите координаты этой точки. Постройте графики
заданных функций в одной системе координат.
имеют
ровно одну общую точку. Определите координаты этой точки. Постройте графики
заданных функций в одной системе координат.
Решение: для нахождения координаты обшей точки данных графиков
функций необходимо решить систему уравнения: 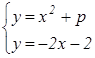 ,
решая которую приходим к квадратному уравнению:
,
решая которую приходим к квадратному уравнению: ![]() .
Опираясь на условия задачи, в которой сказано о наличии только одной общей
точки, делаем вывод, что квадратное уравнение имеет один корень, в случае, если
дискриминант равен нулю.
.
Опираясь на условия задачи, в которой сказано о наличии только одной общей
точки, делаем вывод, что квадратное уравнение имеет один корень, в случае, если
дискриминант равен нулю.
![]()
Подставив значение параметра в полученное квадратное уравнение, находим координату точки пересечения графиков по оси абсцисс:
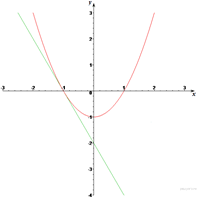
![]()
Строим графики заданных
функций ![]() и
и ![]()
Ответ: координаты точки (-1; 0)
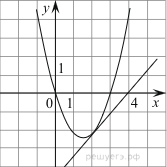
Пример 18. При каких положительных значениях k, прямая ![]() имеет с
параболой
имеет с
параболой ![]() ровно одну общую точку? Найдите
координаты этой точки и постройте графики в одной системе координат?
ровно одну общую точку? Найдите
координаты этой точки и постройте графики в одной системе координат?
Решение: для нахождения координаты обшей точки данных графиков
функций необходимо решить систему уравнения: 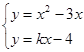 ,
решая которую приходим к квадратному уравнению:
,
решая которую приходим к квадратному уравнению: ![]() .
.
Опираясь на условия задачи, в которой сказано о наличии только одной общей точки, делаем вывод, что квадратное уравнение имеет один корень, в случае, если дискриминант равен нулю.
![]()
 Из двух полученных параметров выбираем тот, который
удовлетворяет условиям задачи
Из двух полученных параметров выбираем тот, который
удовлетворяет условиям задачи ![]() и подставив
данное значение параметра в полученное квадратное уравнение, находим координату
точки пересечения графиков по оси абсцисс:
и подставив
данное значение параметра в полученное квадратное уравнение, находим координату
точки пересечения графиков по оси абсцисс:
![]()
Строим графики заданных
функций с найденным параметром: ![]() и
и ![]()
Ответ: координаты точки (2; –2), k = 1.
Заключение
Подводя итог данной работе, хотелось бы отметить многообразие случаев, на которые были сделаны акценты при выполнении практической части. Хотя, для исследования выбран сравнительно узкий тип заданий с параметрами, вытекающий из графического метода решения уравнений, в условиях которых, по мимо нахождения заданного параметра, требуется демонстрация умения построить график. Кроме того, данные задания играют большую роль в формировании логического мышления и математической культуры учащихся. Чтобы решить такую задачу, необходимо в каждый момент представлять себе, что уже сделано, что еще надо сделать, что означают уже полученные результаты. При решении заданий с параметрами, учащийся должен продемонстрировать глубокое понимание изученного материала, определенную логическую культуру и высокую технику. Недостаточно механическое применение формул, необходимо понимание закономерностей, наличие навыка анализа конкретного случая на основе общих свойств объекта, системность и последовательность в решении, умение объединить рассматриваемые случаи в единый результат.
Целью работы являлось выделение основных типов заданий, связанных с построением графиков, формулирование предписания, необходимого для решения данных заданий, демонстрация применения предписания для решения заданий с параметрами основного курса алгебры. Для достижения поставленной цели потребовалось решение ряда задач. В частности, в первой главе работы нами было определено понятие параметра, описано понятие «уравнение с параметром». Был проведен анализ заданий, имеющихся в основных учебниках по алгебре 7-9 классов, а также описаны теоретические выкладки, применяемые в данных учебниках.
В этой же главе составлено предписание использования графического метода при решении заданий с параметром и определены основные типы заданий с параметром, которые представлены в виде схемы.
Во второй главе приведены примеры решения основных случаев заданий с параметром исследуемого типа, при этом продемонстрированы рассуждению, сопутствующие решению данных заданий.
Таким образом, задачи, поставленные в начале выполнения исследования были решены и цель исследования достигнута.
СПИСОК ЛИТЕРАТУРЫ
1. Виленкин, Н.Я. Алгебра. 8 класс [Текст]: учебник для общеобразовательных учреждений и школ с углубленным изучением математики/ [Н.Я. Виленкин, А.Н. Виленкин, Г.С. Сурвилло и др.] под редакцией Н.Я. Виленкина – М.: Просвещение, 2010.-303 с.
2. Мордкович, А.Г. Алгебра. 8 класс [Текст]: учебник для учащихся общеобразовательных учреждений/ А.Г. Мордкович, Н.П. Николаев – М.: Мнемозина, 2013.-256 с.
3. Дорофеев, Г.В. Алгебра. 9 класс [Текст]: учебник для общеобразовательных учреждений/ [Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др.] под редакцией Г.В. Дорофеева – М.: Просвещение, 2010.-304 с.
4. Макарычев, Ю.Н. Алгебра. 9 класс [Текст]: учебник для учащихся общеобразовательных учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк и др. – М.: Мнемозина, 2008.-447 с.
5. Мордкович, А.Г. Алгебра. 9 класс [Текст]: учебник для учащихся общеобразовательных учреждений/ А.Г. Мордкович, Н.П. Николаев – М.: Мнемозина, 2008.-255 с.
6. Амелькин, В.В. Задачи с параметром [Текст]: справочное пособие по математике/ В.В. Амелькин, В.Л. Рабцевич. – Минск : ООО «Асар», 2004. - 464 с.
7. Крамор, В.С. Задачи с параметром и методы их решения [Текст]: учебное пособие – М.: ООО «Издательство Оникс»: ООО «Издательство «Мир и Образование»», 2007. - 416 с.
8. Мирошин, В.В. Решение задач с параметрами. Теория и практика. [Текст]: пособие– М.: Издательство «Экзамен», 2009. - 286 с.
9. Ястребинецкий, Г.А. Уравнения и неравенства, содержащие параметры [Текст]: пособие для учителей – М.: Просвещение, 1972. - 128 с.
10. Общий толковый словарь русского языка [Электронный ресурс]. – режим доступа http://tolkslovar.ru/p1066.html.
11. Свободная энциклопедия. ВикипедиЯ [Электронный ресурс]. – режим доступа https://ru.wikipedia.org/wiki
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.