Курсовая работа "Двудольные графы"

Введение

Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г. Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики и особенно её приложений дало сильный толчок развитию теории графов. Уже в XIX столетии графы использовались при построении схем.

В настоящее время эта теория находит многочисленное применение в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сети нефтепроводов, в программировании в теории игр, теории передачи сообщений. Теория графов теперь применяется и в таких областях, как экономика, психология и биология.

Цель работы: дать подробную характеристик двудольных графов.

Объект данной работы является: граф

Предмет: двудольный граф

Для достижения намеченной цели перед ставятся следующие задачи:

·                   описать основные понятия теории графов;

·                   дать определение двудольных графов;

·                   дать определение полных двудольных графов;

·                   свойства двудольных графов;

·                   проверка двудольных графов.

 Методологической базой для написания работы послужили общенаучные методы исследования: обобщения, анализа и синтеза, систематизации, а также изучение научной и учебной литературы, технических справочников, самоучителей, материалы различных Интернет-ресурсов.

Курсовая работа состоит из введения, двух глав, заключения, списка используемой литературы. В первой главе рассматривается основные понятия теории графов. Во второй главе предоставлена характеристика двудольных графов.

1. Основные понятия теории графов

Зарождение теории графов в XVIII веке было связано с математическими головоломками, и довольно долго учение о графах рассматривалось как несерьезная тема, прикладное значение которой было связано с играми и развлечениями. В этом отношении судьба теории графов схожа с судьбой теории вероятностей, которая также первоначально рассматривалась в связи с ее применениями к азартным играм. 

В начале XX века графы стали применяться в топологии, и даже в первой половине XX века теория графов считалась главой топологии, этого современного раздела математики. Позже выявились связи теории графов с другими разделами современной математики (например, алгебра, комбинаторика и другие), а различные приложения теории графов к широкому кругу проблем сегодня даже трудно перечислить: это, например, исследования операций и управления, задачи экономики, теории информации, социологии и так далее.

Теория графов — один из фундаментальных разделов дискретной математики. Сведения из этого раздела традиционно включались в курсы кибернетики, а затем и информатики, поскольку графы оказались очень продуктивным средством информационного (математического) моделирования структур систем и процессов, представления задач информационного характера. Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и так далее.

Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, информационных систем, химических и генетических структур, электрических цепей и других систем сетевой структуры. Обычно теорию графов относят к топологии (потому что во многих случаях рассматриваются лишь топологические свойства графов), однако она пересекается со многими разделами теории множеств, комбинаторной математики, алгебры, геометрии, теории матриц, теории игр, математической логики и многих других математических дисциплин. Граф-модели применяются для эффективного использования ресурсов вычислительной системы (оптимизация использования памяти, регистров, уменьшение обменов между оперативной и внешней памятью и так далее), организации больших массивов информации (графы данных для повышения эффективности информационного поиска), увеличения степени параллелизма программы, повышения эффективности работы микропроцессорных и многомашинных систем (распределение процессоров, обмен сообщениями между процессорами, синхронизация). Решение этих и подобных задач привело к появлению множества граф-моделей, связанных как с программами и структурными данными, так и с вычислительными системами.

Основной объект теории графов — граф и его обобщения. Началом теории графов считается 1736 год, когда вышла в свет статья Леонарда Эйлера с его знаменитыми рассуждениями о Кенигсбергских мостах, включающий два берега реки Пергола, два острова в ней и семь соединяющих мостов. Задача состоит в том, чтобы обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку. Задача о Кенигсбергских мостах была решена Эйлером в 1736 году. Затем около 100 лет эта статья оставалась единственной, а методы теории графов невостребованными практикой.

Интерес к графам появился только в середине XIX века благодаря исследованиям электрических сетей, моделей кристаллов и структур молекул. С тех пор сфера применений теории графов непрерывно расширялась и сегодня она представляет собой мощную формальную систему, имеющую необозримое множество областей практического применения. При проектировании компьютерных сетей, телевизионных линий, трубопроводов и строительстве дорог необходимо минимизировать затраты на прокладку коммуникаций. Прежде всего, целесообразно выбрать минимальный по длине маршрут прокладки коммуникаций. Например, необходимо соединить телефонным или оптоволоконным кабелем несколько зданий, расстояния между которыми различны. Возникает задача определения маршрута прокладки кабеля минимальной длины, но при этом к каждому зданию. Для решения таких задач часто используют теорию графов.

Граф — это совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. На рисунке 1 изображен граф, имеющий, пять вершин и шесть ребер. Если рассматривается множество упорядоченных пар точек, то есть на каждом ребре задается направление, то граф называется ориентированным.

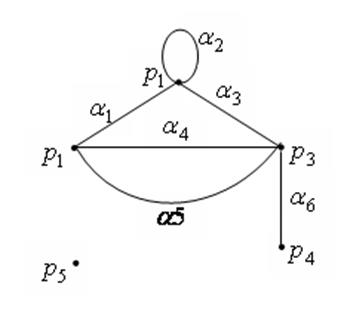
Рисунок 1- граф

Ребра, имеющие одинаковые концевые вершины, называются параллельными. Ребро, концевые вершины которого совпадают, называется петлей. На рисунок 1 а₄ и а₅ — параллельные ребра, a а₆ — петля.

Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой точкой. На рисунок 1 вершина Р₃ и ребро а₃ инцидентны друг другу.

Две вершины, являющиеся концевыми для некоторого ребра, называются смежными вершинами. Два ребра, инцидентные одной и той же вершине, называются смежными ребрами. На рисунок 1 Р₁, Р₂ — смежные вершины, а а₁, а₄ — смежные ребра.

Степенью вершины называется число ребер, инцидентных ей. Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной. 

На рисунок 1 степень вершины Р₁ равна трем, Р₄ —висячая вершина, Р₅ —изолированная.

Граф может быть представлен (сохранен) несколькими способами:

·                     матрица смежности;

·                     матрица инцидентности;

·                     список смежности (инцидентности);

·                     список ребер.

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Размер массива зависит от количества вершин и/или ребер в конкретном графе.

Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.
Число строк матрицы смежности равно числу столбцов и соответствует количеству вершин графа.

·                     0 – соответствует отсутствию ребра,

·                     1 – соответствует наличию ребра.

Матрица смежности и соответствующий ей граф предоставлены на рисунке 2.

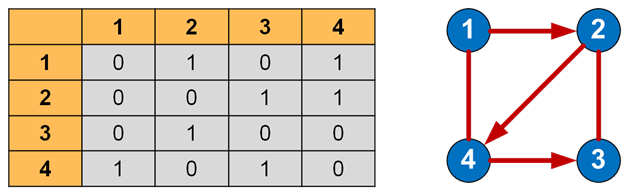
Рисунок 2 - матрица смежности и соответствующий граф

Когда из одной вершины в другую проход свободен (имеется ребро), в ячейку заносится 1, иначе – 0. Все элементы на главной диагонали равны 0 если граф не имеет петель.

Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).

В неориентированном графе если вершина инцидентна ребру, то соответствующий элемент равен 1, в противном случае элемент равен 0.

В ориентированном графе если ребро выходит из вершины, то соответствующий элемент равен 1, если ребро входит в вершину, то соответствующий элемент равен -1, если ребро отсутствует, то элемент равен 0.

Матрица инцидентности для своего представления требует нумерации рёбер, что не всегда удобно.

Матрица инцидентности и соответствующий ей граф предоставлены на рисунке 3

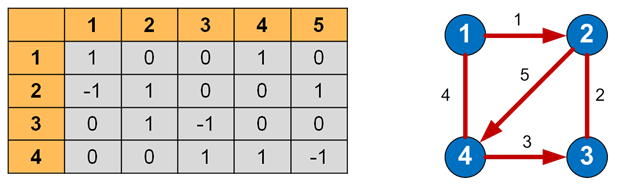
Рисунок 3 - матрица инцидентности и соответствующий ей граф

2.  Двудольный граф

2.1 Определение двудольного графа

Двудольный граф или биграф в теории графов — это граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует рёбер между вершинами одной и той же части.

Все вершины графа можно покрасить в два цвета так, что ребра соединяют только разноцветные вершины (Рисунок 4).

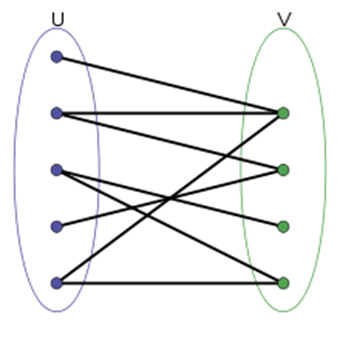
Рисунок 4 – двудольный граф

Полный двудольный граф – двудольный граф, у которого все вершины в разных долях соединены ребрами. (Рисунок 5)

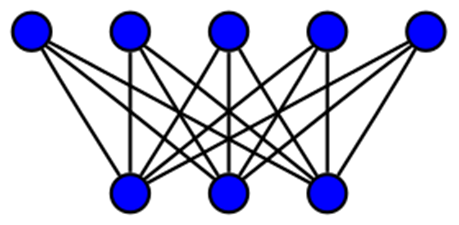
Рисунок 5 – полный двудольный граф

Любое дерево – двудольный граф (в дереве отсутствуют любые циклы, в том числе и нечетные, как показано на рисунке 6).

Рисунок 6 – дерево

Теорема:  – двудольный граф тогда и только тогда, когда все его простые циклы имеют четную длину.

Следствие: всякое дерево, содержащее более одной вершины, является двудольным графом.

Полный двудольный граф (биклика) — специальный вид двудольного графа, у которого любая вершина первой доли соединена со всеми вершинами второй доли вершин.

2.3 Примеры двудольного графа

При моделировании отношений между двумя разными классами объектов двудольные графы очень часто возникают естественным образом. Например, граф футболистов и клубов с преимуществом между игроком и клубом, если игрок играл за этот клуб, является естественным примером аффилированной сети , типа двудольного графа, используемого в анализе социальных сетей .

Другой пример естественного появления двудольных графов - это ( NP-полная ) задача оптимизации железной дороги, в которой входными данными является расписание поездов и их остановок, а цель состоит в том, чтобы найти набор железнодорожных станций как можно меньшего размера, чтобы каждая поезд посещает хотя бы одну из выбранных станций. Эту проблему можно смоделировать как задачу о доминирующем множестве в двудольном графе, имеющем вершину для каждого поезда и каждой станции и ребро для каждой пары станции и поезда, который останавливается на этой станции.

Третий пример - академическая нумизматика. Старинные монеты созданы с использованием двух положительных впечатлений от дизайна (аверс и реверс). Таблицы, которые нумизматы создают для представления производства монет, представляют собой двудольные графики.

Более абстрактные примеры включают следующее:

·                    Каждое дерево двудольное.

·                    Циклические графы с четным числом вершин двудольны.

·                    Каждый плоский граф , все грани которого имеют четную длину, двудольный. Частными случаями этого являются сеточные графы и квадратные графы , в которых каждая внутренняя грань состоит из 4 ребер, а каждая внутренняя вершина имеет четырех или более соседей.

·                    Полный двудольный граф на т и п вершин, обозначим через К _{п, т} представляет собой двудольный граф, где U и V являются непересекающиеся множества размера т и п , соответственно, и Е соединяет каждую вершину в U со всеми вершинами из V . Отсюда следует, что K _{m, n} имеет mn ребер. Тесно связанные с полными двудольными графами являются графы короны , образованные из полных двудольных графов путем удаления ребер идеального соответствия .

·                    Графы гиперкубов , частичные кубы и медианные графы двудольные. В этих графах вершины могут быть помечены битовыми векторами таким образом, что две вершины являются смежными тогда и только тогда, когда соответствующие битовые векторы отличаются в одной позиции. Двудольное деление может быть образовано путем отделения вершин, битовые векторы которых имеют четное число единиц, от вершин с нечетным числом единиц. Деревья и квадратные графы образуют примеры медианных графов, и каждый медианный граф является частичным кубом

2.4 Свойства Двудольного графа

Характеристика:

Двудольные графы можно охарактеризовать по-разному:

·                     Граф двудольный тогда и только тогда, когда он не содержит нечетного цикла .

·                     Граф двудольный тогда и только тогда, когда он двукратно раскрашен (то есть его хроматическое число меньше или равно 2).

·                     Спектр графа симметричен тогда и только тогда, когда это двудольный граф.

Теорема Кёнига и совершенные графы:

В двудольных графах размер минимального покрытия вершин равен размеру максимального соответствия ; это теорема Кёнига . Альтернативная и эквивалентная форма этой теоремы состоит в том, что размер максимального независимого множества плюс размер максимального соответствия равен количеству вершин. В любом графе без изолированных вершин размер минимального покрытия ребер плюс размер максимального совпадения равняется количеству вершин. (Рисунок 7)

Объединение этого равенства с теоремой Кёнига приводит к тому факту, что в двудольных графах размер минимального покрытия ребер равен размеру максимального независимого множества, а размер минимального покрытия ребер плюс размер минимального покрытия вершин равно количеству вершин.

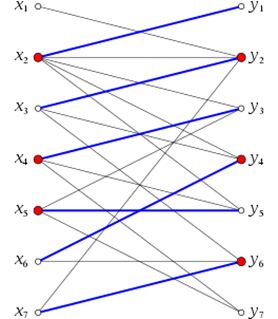
Рисунок 7 – теорема Кёнига

Другой класс связанных результатов касается совершенных графов : каждый двудольный граф, дополнение к каждому двудольному графу, линейный граф каждого двудольного графа и дополнение к линейному графу каждого двудольного графа являются совершенными. Совершенство двудольных графов легко увидеть (их хроматическое число равно двум, и их максимальный размер клики также равен двум), но совершенство дополнений двудольных графов менее тривиально и является еще одним переформулированием теоремы Кёнига. Это был один из результатов, который мотивировал первоначальное определение совершенных графов. Совершенство дополнений к линейным графам совершенных графов - это еще одно повторение теоремы Кёнига, а совершенство самих линейных графов - это повторение более ранней теоремы Кёнига о том, что каждый двудольный граф имеет раскраску ребер с использованием количества цветов, равных его максимальная степень.

Согласно сильной теореме о совершенном графе , совершенные графы имеют характеристику запрещенного графа, аналогичную характеристике двудольных графов: граф является двудольным тогда и только тогда, когда он не имеет нечетного цикла в качестве подграфа, а граф совершенен тогда и только тогда, когда он имеет нет нечетного цикла или его дополнения как индуцированного подграфа .

Двудольные графы, линейные графы двудольных графов и их дополнения образуют четыре из пяти основных классов совершенных графов, используемых в доказательстве сильной теоремы о совершенных графах.

Матрица из двудольного графа является (0,1) матрицами размера, который имеет по одному для каждой пары смежных вершин и нуля для несмежных вершин. Матрицы взаимосопряженности могут использоваться для описания эквивалентностей между двудольными графами, гиперграфами и ориентированными графами. (U,V,E)

 Гиперграф является комбинаторной структурой, которая, как и неориентированным граф, имеет вершины и ребро, но в которых ребро может быть произвольным множество вершин вместо того, чтобы иметь ровно два конечные точки.

Двудольный граф может быть использован для моделирования гиперграфа, в котором U — это множество вершин гиперграфа, V - множество гиперребер, а E содержит ребро от вершины гиперграфа v до ребра гиперграфа e именно тогда, когда v является одним из конечные точки e. При этом соответствии матрицы двойственности двудольных графов являются в точности матрицами инцидентности соответствующих гиперграфов.

Как частный случай этого соответствия между двудольными графами и гиперграфами, любой мультиграф (граф, в котором может быть два или более ребра между одними и теми же двумя вершинами) может быть интерпретирован как гиперграф, в котором некоторые гиперребра имеют равные множества конечных точек, и представлен двудольным графом, не имеющим множественных смежностей и в котором все вершины на одной стороне двудольного графа имеют степень два(U,V,E).

Аналогичная переинтерпретация матриц смежности может использоваться, чтобы показать взаимно однозначное соответствие между ориентированными графами (на заданном количестве помеченных вершин, допускающих петли) и сбалансированными двудольными графами с одинаковым количеством вершин по обе стороны от двудольность.

В самом деле, матрица смежности ориентированного графа с n вершинами может быть любой (0,1) матрицей размера , которая затем может быть интерпретирована как матрица смежности двудольного графа с n вершинами на каждой стороне его двудольного графа . В этой конструкции двудольный граф является двудольным двойным покрытием ориентированного графа n*n.

2.5 Проверка двудольного графа

Для того, чтобы проверить граф на предмет двудольности, достаточно в каждой компоненте связности выбрать любую вершину и помечать оставшиеся вершины во время обхода графа (например, поиском в ширину) поочерёдно как чётные и нечётные (см. иллюстрацию). Если при этом не возникнет конфликта, все чётные вершины образуют множество {\displaystyle U}U, а все нечётные — V {\displaystyle V}.

Алгоритм проверки графа на двудольность обычно даётся в курсе алгоритмов как один из простейших графовых алгоритмов. Его идея прямолинейна: сначала каким-то образом кладутся вершины в левую или правую долю, а при обнаружении конфликтного ребра утверждаем, что граф не является двудольным.

Чуть подробнее: сначала кладётся какая-то вершина в левую долю. Очевидно, все соседи этой вершины должны лежать в правой доле. Далее, все соседи соседей этой вершины должны лежать в левой доле, и так далее. Продолжается назначение вершинам доли до тех пор, пока в компоненте связности вершины, с которой начинали, ещё есть вершины, которым не назначили соседей. Затем повторяется это действие для всех компонент связности.

Если есть ребро между вершинами, попавшими в одну и ту же долю, несложно найти в графе нечётный цикл, как широко известно (и достаточно очевидно) невозможный в двудольном графе. Иначе есть корректное разбиение на доли, а значит, граф является двудольным.

Как правило, этот алгоритм реализуют с помощью поиска в ширину или поиска в глубину. В императивных языках обычно используют поиск в глубину, как чуть-чуть более простой и не требующий дополнительных структур данных.

Таким образом получаем следующую схему. Обходятся вершины графа с помощью поиска в глубину и назначаем им доли, меняя номер доли при переходе по ребру. Если пытаться назначить долю вершине, у которой доля уже назначена, можно смело утверждать, что граф не является двудольным. В тот момент, когда всем вершинам назначена доля и просмотрены все рёбра, получается разбиение.

2.6 Соответствие двудольных графов

Соответствия в графе представляет собой подмножество его ребер, никакие два из которых разделяют конечную точку. Алгоритмы с полиномиальным временем известны для решения многих алгоритмических проблем сопоставлений, включая максимальное сопоставление (поиск сопоставления, в котором используется как можно больше ребер), сопоставление максимального веса и стабильное сопоставление . Во многих случаях задачи сопоставления проще решить на двудольных графах, чем на недвудольных графах, и многие алгоритмы сопоставления, такие как алгоритм Хопкрофта – Карпа для сопоставления максимальной мощности, работают правильно только на двудольных входных данных.

В качестве простого примера предположим, что все люди ищут работу из набора рабочих мест, причем не все люди подходят для всех рабочих мест. Эту ситуацию можно смоделировать как двудольный граф, в котором ребро соединяет каждого соискателя с каждой подходящей работой. Совершенное паросочетание описывает способ одновременно удовлетворяющий всем лицам , ищущим работу и заполнить все рабочие места; Теорема Холла о браке дает характеристику двудольных графов, которые допускают совершенное сопоставление. 

Национальный Resident Matching Программа применяет методы график соответствия, чтобы решить эту проблему для американских медицинских студентов, ищущих работу и больницы ординатуры рабочих мест.PJ(P,J,E)

Двудольные графы широко используются в современной теории кодирования , особенно для декодирования кодовых слов, полученных из канала. Примером этого являются факторные графы и графы Таннера .

Граф Таннера (Рисунок 8)— это двудольный граф, в котором вершины на одной стороне двудольного раздела представляют цифры кодового слова, а вершины на другой стороне представляют собой комбинации цифр, которые, как ожидается, будут без ошибок равны нулю в кодовом слове. Факторный граф - это тесно связанная сеть убеждений, используемая для вероятностного декодирования LDPC и турбокодов .

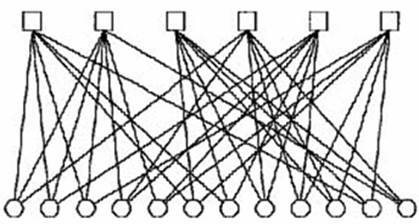
Рисунок 8 - граф Таннера

В информатике сеть Петри  — это инструмент математического моделирования, используемый для анализа и моделирования параллельных систем. Система моделируется как двудольный ориентированный граф с двумя наборами узлов: набором узлов «места», которые содержат ресурсы, и набором узлов «событий», которые генерируют и / или потребляют ресурсы. Есть дополнительные ограничения на узлы и ребра, которые ограничивают поведение системы. В сетях Петри используются свойства двудольных ориентированных графов и другие свойства, позволяющие проводить математические доказательства поведения систем, а также упрощая реализацию моделирования системы. Простейшая модель сети Петри для моделирования предоставлена на рисунке 9.

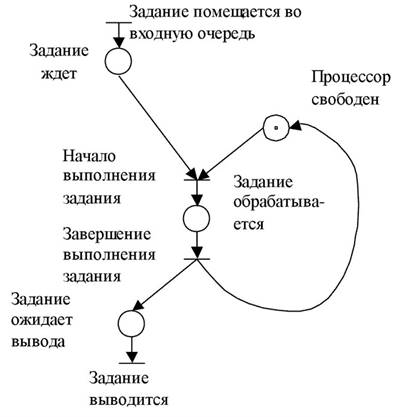
Рисунок 9 – сеть Петри

В проективной геометрии , Леви графики являются формой двудольного графа используется для моделирования числа случаев между точками и линиями в конфигурации .

В соответствии с геометрическим свойством точек и линий, что каждые две прямые пересекаются не более чем в одной точке и каждые две точки соединяются одной линией, графы Леви обязательно не содержат циклов длины четыре, поэтому их обхват должен быть шесть или более. Граф Леви с восемнадцатью вершинами изображён на рисунке 10.

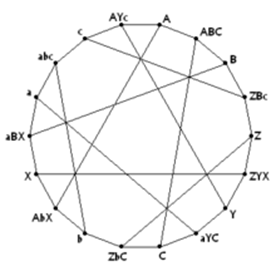
Рисунок 10 – граф Леви

Заключение

Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г. Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики и особенно её приложений дало сильный толчок развитию теории графов. Уже в XIX столетии графы использовались при построении схем.

В настоящее время эта теория находит многочисленное применение в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сети нефтепроводов, в программировании в теории игр, теории передачи сообщений. Теория графов теперь применяется и в таких областях, как экономика, психология и биология.

В ходе проделанной работы достигнута цель дана подробная характеристика двудольных графов.

Объектом данной работы являлся граф, предметом двудольный граф.

Так же для достижения намеченной цели были выполнены следующие задачи:

·                   описаны основные понятия теории графов;

·                   дано определение двудольных графов;

·                   дано определение полных двудольных графов;

·                   рассмотрены свойства двудольных графов;

·                   предоставлена проверка двудольных графов.

 Методологической базой для написания работы послужили общенаучные методы исследования: обобщения, анализа и синтеза, систематизации, а также изучение научной и учебной литературы, технических справочников, самоучителей, материалы различных Интернет-ресурсов.

Список используемой литературы

1.                 Виды графов. [Электронный ресурс] - Режим доступа: https://knowledge.allbest.ru- Заглавие с экрана - (Дата обращения: 16.05.2019)

2.                 Граф в математике. [Свободная электронная энциклопедия]. – Режим доступа: https://ru.wikipedia.org. – заглавие с экрана – (Дата обращения: 16.05.2019)

3.                 Граф. [электронный ресурс] – режим доступа: https://prog-cpp.ru – заглавие с экрана – (дата обращения: 16.05.2019)

4.                 Графы – Математика [электронный учебник] – режим доступа: https://foxford.ru – заглавие с экрана – (дата обращения: 16.05.2019)

5.                  Двудольность [Электронный ресурс] - Режим доступа: https://e-maxx.ru- Заглавие с экрана - (Дата обращения: 16.05.2019)

6.                 Двудольные графы [Электронный ресурс] - Режим доступа: https://logic.pdmi.ras.ru- Заглавие с экрана - (Дата обращения: 16.05.2019)

7.                 Двудольные графы [Электронный ресурс] - Режим доступа: http://stu.alnam.ru- Заглавие с экрана - (Дата обращения: 16.05.2019)

8.                 Двудольные графы [Электронный ресурс] - Режим доступа: https://mipt.lectoriy.ru- Заглавие с экрана - (Дата обращения: 16.05.2019)

9.                 Двудольные графы. [Электронный ресурс] - Режим доступа: https://dic.academic.ru- Заглавие с экрана - (Дата обращения: 16.05.2019)

10.            Двудольный граф [Электронный ресурс] - Режим доступа: https://ru.wikipedia.org- Заглавие с экрана - (Дата обращения: 16.05.2019)

11.            Применение графов в различных областях жизни людей. [Электронный ресурс] – режим доступа: http://obuchonok.ru – заглавие с экрана – (Дата обращения: 16.05.2019)

12.            Свойства двудольных графов [Электронный ресурс] - Режим доступа: https://lms2.sseu.ru- Заглавие с экрана - (Дата обращения: 16.05.2019)

13.            Теория графов. [электронный источник] – режим доступа: https://studfiles.net – заглавие с экрана – (дата обращения: 16.05.2019)

14.            Теория графов. Основные понятия и виды графов. [Электронный ресурс] - Режим доступа: http://kvodo.ru. –  заглавие с экрана - (Дата обращения: 16.05.2019)

15.            Скачано с www.znanio.ru