
Квадратный
корень из произведения и дроби
при преобразовании выражений с корнем
Цели: продолжить формирование умения применять свойства квадратного корня при преобразовании выражений.
Ход урока
I. Организационный момент.
II. Устная работа.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
г) 2
;
г) 2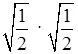 ;
;
д) ![]() ; е)
; е) 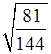 ; ж)
; ж) ![]() ;
з)
;
з) 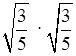 ;
;
и) ![]() ; к)
; к) 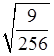 .
.
III. Формирование умений и навыков.
1. № 372, № 387 (а, в, д, ж).
2. № 374.
Р е ш е н и е
Это задание может вызвать затруднения у
учащихся. Раньше им встречались выражения вида ![]() , в которых
, в которых ![]() и
и ![]() извлекались.
При выполнении данного номера это свойство корней напрямую применять
нецелесообразно.
извлекались.
При выполнении данного номера это свойство корней напрямую применять
нецелесообразно.
Необходимо подкоренное выражение представить в виде произведения таких множителей, из которых корень извлекается.
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() ;
;
д) ![]() ;
;
е) ![]() ;
;
ж) ![]() ;
;
з) ![]() .
.
3. № 376.
При выполнении этого задания учащиеся довольно
часто допускают следующую ошибку: ![]() = 13 – 12 = 1.
= 13 – 12 = 1.
В этом случае следует предложить учащимся вычислить значение подкоренного выражения, извлечь корень и сравнить полученные результаты.
Данный пример помогает избежать подобных ошибок в дальнейшем и еще раз заостряет внимание учащихся на свойствах квадратных корней.
Если в примерах а) и б) учащиеся просто могут вычислить значение подкоренного выражения и извлечь корень, то в следующих примерах это можно сделать только при помощи калькулятора. Чтобы учащиеся «увидели» формулу разности квадратов, нужно требовать вычислений без калькулятора.
в) ![]() ;
;
д) ![]()
![]() .
.
4. № 380.
Р е ш е н и е
а) 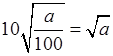 .
.
– Преобразуем выражение, стоящее в правой части равенства:
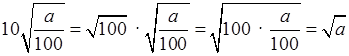 .
.
б) ![]() .
.
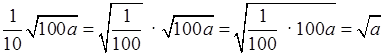 .
.
Некоторым сильным в учебе учащимся дополнительно можно предложить выполнить задания по карточкам.
К а р т о ч к а № 1
1. Расположите в порядке возрастания числа: 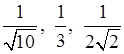 .
.
2. Найдите значение выражения:
а) ![]() ; б)
; б) ![]() ;
;
в) 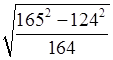 .
.
К а р т о ч к а № 2
1. Расположите в порядке возрастания числа: 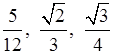 .
.
2. Найдите значение выражения:
а) ![]() ; б)
; б) ![]() ;
;
в) 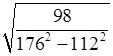 .
.
Р е ш е н и е заданий карточки № 1.
1. Все дроби имеют числители, равные 1. Поэтому достаточно сравнить знаменатели дробей. Имеем:
2![]() < 3 <
< 3 < ![]() , поэтому
, поэтому 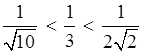 .
.
2. а) ![]()
= 10 · 11 · 6 = 660;
б) ![]()
![]()
= 2160;
в) 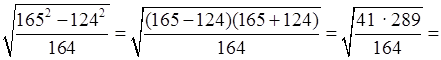
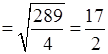 = 8,5.
= 8,5.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сформулируйте свойство вычисления корня из произведения неотрицательных чисел.
– Сформулируйте свойство вычисления корня из частного от деления неотрицательного числа на положительное число.
– Сформулируйте правила умножения и деления корней.
– Как преобразовать выражение вида ![]() , если
корни из чисел х и у не извлекаются?
, если
корни из чисел х и у не извлекаются?
Домашнее задание: № 373, № 375, № 377 (б, г, е), № 387 (б, г, е, з).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.