Лабораторная работа № 5. ИЗУЧЕНИЕ СВОЙСТВ ЛИНЕЙНОГО НЕЙРОНА И ЛИНЕЙНОЙ НЕЙРОННОЙ СЕТИ

Лабораторная работа № 5. ИЗУЧЕНИЕ СВОЙСТВ ЛИНЕЙНОГО НЕЙРОНА И ЛИНЕЙНОЙ НЕЙРОННОЙ СЕТИ

Цель работы

Изучить свойства линейного нейрона и линейной нейронной сети.

Основные теоретические положения

            Модель нейрона. Искусственные нейронные сети (НС) представляют собой простейшие математические модели мозга. Понять основные принципы построения НС можно, рассматривая их как совокупность (сеть) отдельных структур (нейронов). Очень грубо структуру биологического нейрона можно описать следующим образом. Нейрон имеет сому – тело, дерево входов – дендриты, выход – аксон. На соме и на дендритах распола­гаются окончания аксонов других нейронов, называемых си­напсами. Принятые синапсами входные сигналы стремятся либо возбудить нейрон, либо затормозить. Когда суммарное возбуждение достигает некоторого порога, нейрон возбуждается и посылает по аксону сигнал другим нейронам. Каждый синапс обладает уникальной синаптической силой, которая пропорционально своему значению изменяет передаваемый на нейрон входной сигнал. В соответствии с приведенным описа­нием математическая модель нейрона представляет собой суммирующий пороговый элемент (рис. 1).

         Формула срабатывания нейрона:

            Алгоритм обучения по дельта-правилу. Обучение НС происходит на некоторой обучающей выборке, для каждого образца которой определяются и сравниваются с желаемыми значениями все текущие выходы. Если разница недопустима, то веса изменяются. Окончанием обучения считается ситуация, когда общая ошибка на всех образцах допустима.

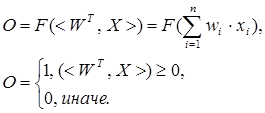
         Все алгоритмы обучения нейросетей являются разновидностями алгоритма обучения по методу коррекции ошибки, которая осуществляется по-разному. Идея изменения весов НС сводится к нахождению общей меры качества сети, в качестве которой обычно выбирают функцию ошибки сети. Тогда, чтобы подобрать нужные веса, необходимо минимизировать функцию ошибки. Самым распространенным методом поиска минимума является метод градиентного спуска. Для случая функции с одной переменной веса изменяются в направлении, противоположном производной, т. е. справедлива формула:

где  h – некоторый уровень обучения, шаг изменения;

F'(W) – производная функции качества НС для одной переменной.

         Для функции F от n переменных и единичного вектора е в пространстве Rⁿ ||е|| = 1, , дифференциал выражается формулой:

.

         Для случая е = (0, 0...1...0) определим частный дифференциал:

.

         Таким образом, антиградиент – это набор следующих дифференциалов:

         Для определения обобщенной функции ошибки рассмотрим обучающую выборку {(х^k, y^k)}, где k = 1, ..., К. Накопленная по всем эпохам ошибка:

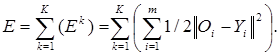
         Формула модификации весов НС:

уточняется для различных видов функции активации. Для линейной функции F(t) = t, НС формирует каждый выход как скалярное произведение весов на вектор входов:  и градиент будет равен:

где Y_i – желаемый выход; O_i – полученный выход; X – вектор выхода.

         Таким образом, получаем формулу изменения весов:

         Если значением  назвать разницу (Y_i – О_i), то получим формулу:

что является алгоритмом обучения по -правилу.

         Описание основных функций. Для работы с нейронными сетями необходимо инсталлировать MATLAB и обладать первоначальными знаниями относительно языка системы. Поскольку MATLAB представляет собой интерпретатор, то обучение инструментарию нейронных сетей заключается в основном в изучении функций и их параметров. Узнать возможности нейрона как классификатора простых линейно сепарабельных задач можно путем проведения экспериментов с моделью одного линейного нейрона.

         Функция newp. Для того чтобы создать нейрон, используют функцию newp, имеющую следующий синтаксис:

где PR – матрица минимальных и максимальных R входных эле­ментов; S – количество нейронов (при создании одного нейрона S = 1); TF – функция активации (transfer function); LF – имя функции обучения нейрона.

         В случае если параметры функции newp не заданы, их зна­чения определяются посредством ввода значений в диалого­вые окна. Построенный нейрон характеризуется функциями весов (weight function), входов сети (net input function) и оп­ределенной функцией активации. Функция весов – это ум­ножение весов на входной сигнал, функция входов сети – их сумма. Веса задаются как для входов нейрона, так и для фик­сированного входа, задающего порог срабатывания (bias). Вектор весов инициализируется нулями. Для обучения ис­пользуются функции, рассмотренные ниже.

         Функция learnp настраивает веса нейрона. Синтаксис функции обучения довольно сложен:

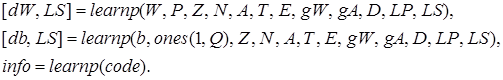
         Функция learnp (W, P, Z, N, A, T, E, gW, gA, D, LP, LS) имеет несколько входов, где вектор W – вектор весов; Р – вектор входов; Z – вектор взвешенных входов; N – вектор сети; А – вектор выхода; Т – вектор желаемых выходов; Е – вектор ошибок; gW – вектор изменения весов; gA – изменения вы­ходов. Функция возвращает значения: dW – изменения мат­рицы весов; LS – новый уровень обученности.

         Функция learnp может быть использована с параметрами по умолчанию:

         Использование пустого списка [ ] означает параметр по умолчанию.

         Функция learnp вычисляет изменение весов dW для заданного нейрона в соответствии с правилом обучения персептрона:

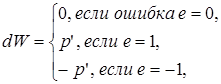
т.е. .

         Функция learnpn настраивает нормализованные веса:

         Функция learnpn вычисляет изменение весов dW для данного нейрона и его входа Р и ошибки Е в соответствии с нор­мализованным правилом обучения персептрона:

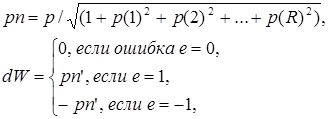
т.е. .

         Линейный нейрон имеет одно существенное ограничение. Входные векторы должны быть линейно разделимы. Если векторы невозможно отделить прямой или гиперплоскостью, то персептрон не способен решить задачу классификации.

         Функция adapt адаптирует НС к условиям задачи:

         Параметры функции adapt: net – имя сети; Р – входы сети; T – желаемый выход; Р_i – исходные условия задержки; A_i – ис­ходные условия задержки для слоя. Функция возвращает па­раметры адаптированной сети net.adaptParam: net – изменен­ная сеть; Y – выход сети; Е – ошибки сети; Pf – условия за­держки входов; Af – условия задержки слоя. Параметры Р_i и Pf необязательные и необходимы только для сетей, имеющих задержки на входах и слое.

         Функция train также обучает НС и использует следующий синтаксис:

         Функция train имеет следующие параметры: net – сеть; Р – входы сети;    Т – желаемый выход; Р_i – исходные условия задержки входа; A_i – исходные условия задержки слоя.

         Функция  sim имитирует нейронную сеть:

где net – сеть; Р – входы сети; P_i — исходные условия задержки входов сети;   A_i – исходные условия задержки слоя. Функция возвращает Y – выходы сети;   Pf – окончательные условия задержки входов; Af – окончательные условия задержки слоя.

         Функции активации. Ниже представлены назначения этих функций.

         Функции графического интерфейса и вспомогательные функции. Назначение этих функций представлено ниже.

            Структура данных описания нейронных сетей. Структура данных net – это описание обученной НС. Обучение осуществляется в соответствии со следующими параметрами, значения которых либо устанавливаются пользователем, либо по умолчанию.

            Структура данных описания адаптированной НС net.adaptfcn включает в себя следующие поля net.adapt.param: NET – адаптированная НС; Y – выходы НС; Е – ошибки НС; Pf – окончательные входные значения задержек;                Af – окончательные выходные задержки; TR – результат обучения (эпохи и целевая ошибка). Проведем в среде MATLAB toolbox эксперименты, используя рассмотренные функции.

Скачано с www.znanio.ru