Лабораторная работа № 6. Изучение многослойного нелинейного персептрона и алгоритма обратного распространения ошибки

Цель работы

Изучить возможности многослойного персептрона как аппроксиматора и классификатора.

Основные теоретические положения

Алгоритм обратного распространения ошибки. Пусть определена трехслойная нейронная сеть с п входами, m выходами и l скрытыми между ними элементами, тогда необходимо рассмотреть и построить два слоя весов: от входов к скрытым элементам и к выходу, т. е. (W₁, W₂).

         Назначение алгоритма обратного распространения ошибки – настройка всех слоев многослойной структуры. Рассмотрим работу алгоритма на примере сети с одним скрытым слоем и одним выходом (рис. 5). Преобразования входных сигналов, задаваемые нейронной сетью, определяются следующими формулами:

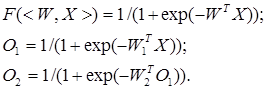
         Общая функция ошибки зависит от весов всех слоев, в нашем случае от вектора W₂ и от матрицы W₁:

где Y – выход, который задан в обучающей выборке.

                   Ошибка! Ошибка связи.

Рис. 5. Многослойный персептрон

         Теперь необходимо определить приращение каждого веса с помощью частных производных:

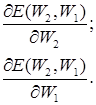
         Для многослойной архитектуры частные производные ошибки по матрице весов каждого слоя определяются по формуле сложной производной. В случае униполярной сигмоиды правило изменения весов будет следующим:

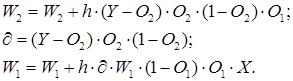
         Таким образом, метод обратного распространения ошибки позволяет изменять веса промежуточных слоев, хотя желаемые значения на промежуточных слоях не заданы.

         Описание основных функций. Функция newff создает нейронную сеть прямого распространения сигнала, обучаемую с помощью алгоритма обратного распространения ошибки:

         net = newff(PR, [S1 S2 SNl], {TF1 TF2 TFNl), BTF, BLF, PF).

Рассмотрим параметры функции newff: PR – матрица интервалов значений для R входных элементов, задаваемых минимальным и максимальным значениями; S_i – размер i-го слоя, для N слоев; TF_i – функция активации i-го слоя, по умолчанию используется функция tansig – гиперболический тангенс; BTF – функция обучения сети методом обратного распространения ошибки, по умолчанию используется функция traingdx; BLF – функция изменения весов при обучении, по умолчанию используется learngdm; PF – функция измере­ния ошибки, по умолчанию тsе. Функция newff возвращает многослойную нейронную сеть прямого и обратного распро­странения сигнала и ошибки соответственно. Функции акти­вации могут быть выбраны из следующего перечня: гипербо­лический тангенс tansig, логистическая сигмоида logsig или линейная функция purelin.

         3 Порядок выполнения работы

         Пример 1. Создание и обучение нейронной сети с помощью алгорима обратного распространения ошибки

         Зададим с помощью графика исходную функцию:

% входы НС

P = [0 1 2 3 4 5 6 7 8];

% желаемые реакции НС

T = [0 0.44 0.88 0.11 -0.66 -0.95 -0.45 0.18 0.92];

% изображение аппроксимируемой функции

plot(P, T, 'o');

         Используем функцию newff, чтобы создать двухслойную сеть прямого распространения. Пусть сеть имеет входы с интервалом значений от 0 до 8, первый слой с 10 нелинейными сигмоидальными, второй – с одним линейным нейронами. Используем для обучения алгоритм обратного распространения ошибки (backpropagation) Левенберга – Марквардта (рис. 6).

% создание двухслойной НС прямого распространения с интервалом

% значений входов от 0 до 8, причем первый слой содержит

% 10 нелинейных сигмоид, а второй — один линейный нейрон.

% Для обучения используется алгоритм обратного распространения

% ошибки (backpropagation).

net = newff([0 8], [10 1], {'tansig' 'purelin'},'trainlm');

% имитация работы необученной НС

yl = sim (net, P);

% изображение результатов работы необученной НС

plot(P, T, 'o', P, yl, 'x') ;

% Обучим сеть на 100 эпохах с целевой ошибкой 0.01:

% установка количества проходов

net.trainParam.epochs = 50;

% установка целевого значения ошибки

net.trainParam.goal = 0.01;

% обучение НС (рис. 6)

net = train(net, P, T) ;

% имитация работы обученной НС

y2 = sim(net,  P);

% изображение результатов работы НС (рис. 7)

plot(P, T, 'o', P, yl, 'x', P, y2, '+');

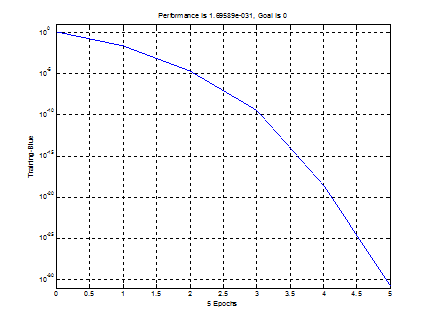
Рис. 6. График обучения двухслойного персептрона

         Для исследования работы алгоритма обратного распространения ошибки воспользуемся примером, встроенным в MATLAB toolbox, набрав команду demo.

         В появившемся диалоговом окне необходимо последовательно выбирать пункты меню: Toolboxes->Neural Network->Other Demos->Other Neural Network Design textbook demos->Table of Contents->10-13->Backpropagation Calculation.

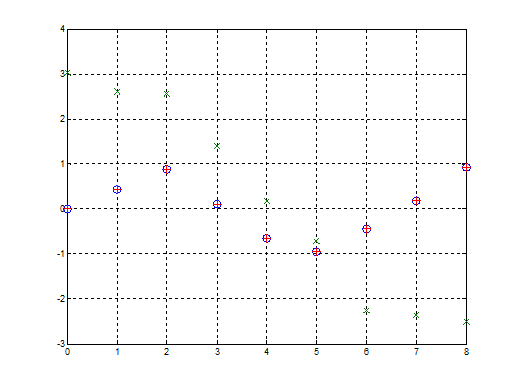
Рис. 7. Результат аппроксимации векторов двухслойным персептроном

         В примере используется двухслойный персептрон с двумя нелинейными нейронами в первом слое и одним во втором. Действие алгоритма обратного распространения ошибки разбито на следующие шаги: назначение входа и желаемого вы­хода, прямой проход входного сигнала до выхода, обратное распространение ошибки, изменение весов. Переменные, по­зволяющие проследить работу алгоритма обратного распро­странения ошибки, обозначены следующим образом:

         Р – входной сигнал;

         W₁(i) – вектор весов первого слоя, W₁(1) – вес связи, пе­редающий входной сигнал на первый нейрон, a W₁(2) – на второй;

         W₂(i) – вектор весов второго слоя, W₂(1) – вес связи, пе­редающий входной сигнал с первого нейрона во второй слой, a W₂(2) – со второго;

         B₁(i) – вектор пороговых значений (bias) нейронов пер­вого слоя, i = 1, 2;

         В₂ – пороговое значение (bias) нейрона второго слоя;

         N₁(i) – вектор выходов первого слоя, i = 1, 2;

         N₂ – выход второго слоя;

         A₁(i) – вектор выходных сигналов первого слоя после вы­полнения функции активации (сигмоиды), i = 1, 2;

         А₂ – выход второго слоя после выполнения функции ак­тивации (линейной);

         lr –  коэффициент обучаемости.

         Пусть входной сигнал Р = 1,0, а желаемый выход .

         Результаты выполнения этапов алгоритма обратного распространения ошибки представлены в табл. 1.

Таблица  1

Контрольные вопросы

1       Каким алгоритмом обучают многослойные НС?

2       Из каких основных этапов состоит алгоритм обратного распространения ошибки?

3       Почему алгоритм обратного распространения ошибки от­носится к классу алгоритмов градиентного спуска?

4       Как влияет функция принадлежности на правило измене­ния весов в обратном алгоритме распространения ошибки?

5       Какая функция в среде MATLAB создает НС прямого распространения?

6       Какие функции активации могут быть назначены для нейронов НС прямого распространения?

Скачано с www.znanio.ru