Поделиться
Л2-00257.docx
Разработка алгоритмов и программирование задач с использованием процедур и функций
Цель: освоить методы разработки алгоритмов и программирование задач использованием процедур и функций.
Краткие теоретические сведения
На практике часто встречаются случаи, когда по ходу выполнения расчетов в задачах приходится проводить одни и те же вычисления, но при различных исходных данных. Чтобы исключить повторение одинаковых действий и сделать тем самым алгоритм проще и понятнее, можно выделить повторяющиеся действия в самостоятельную часть в виде вспомогательной подзадачи, которая может быть использована многократно по мере необходимости. Такая вспомогательная подзадача, реализующая определенный алгоритм и которая допускает обращение к ней из разных частей блок-схемы основной задачи, называется подпрограммой.
Подпрограммы оформляются в виде отдельных алгоритмов, которые имеют четко обозначенный вход и выход. При составлении блок-схемы основной задачи обязательно надо предусмотреть обращение к подпрограмме.
Подпрограммы бывают двух видов: процедуры и функции. Основное отличие их заключается в том, что результат работы процедуры - это целый набор значений, а результат выполнения функции - это одно значение.
Пример 1. Вычислить разницу средних арифметических значений элементов массива Х=(Х1, Х2 .., Х50) с четными индексами и элементов с нечетными индексами:
R = 1
25
50
Xi
i=2,4,...
- 1
25
49
Xi
i=1,3,...
Для вычисления переменной R необходимо дважды определить среднее арифметическое значение 25 чисел. Поэтому в качестве вспомогательной подзадачи можно выделить вычисление среднего арифметического значения 25 чисел:
S = 1
25
åX j
j=k,k+ 2,....
100
Первый раз необходимо задать k=1 и n=49, а второй раз - k=2 и n=50. Вспомогательную подзадачу можно оформить в виде функции. Блок-схема алгоритма вспомогательной подзадачи начинается стрелкой «вход» с указанием списка исходных данных, а заканчивается стрелкой «выход» со списком выходных данных. Результат функции присваивается переменным S1, S2.
Схема алгоритма подпрограммы функции SUM имеет вид:
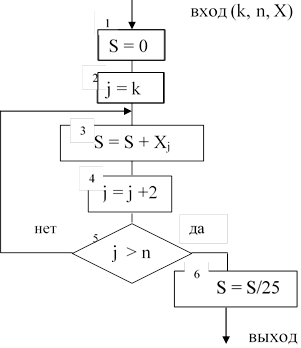(S)
Схема алгоритма основной задачи имеет вид:
 |
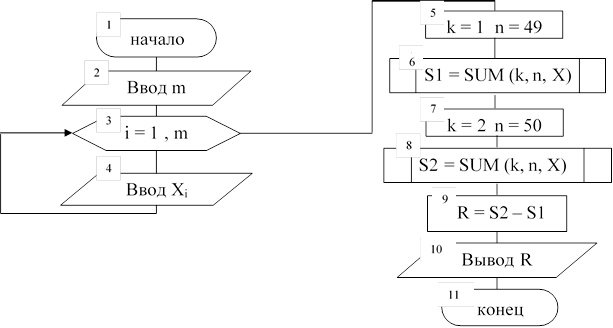101
Пример 2. Составить таблицы значений функций
g(x) = 3,7x3 - 0,8
и z(x) = -0,75x3 +1,2
, если
1£ x £10
Dx = 0,5
с использованием подпрограммы функции.
Предусмотреть ввод значения переменной а.
Решение.
Исходные данные: хн, хк, ∆х, а.
Результат вычислений: значения g(x) и z(x) для каждого значения х.
Значения функций вычисляются по общей формуле:
y(n) = bn3 + c
При исходных данных b=3.7; c=-0.8; d=2.5; n=x; m=a вычисляются значения функции g(x), а при b=-0.75; c=1.2; d=-0.6; n=x; m=a вычисляются значения функции z(x).
Схема алгоритма подпрограммы функции имеет вид:
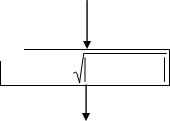вход (n, m, b, c, d)
1
y= bn3 + c
msin 2 n + d
выход (y)
Схема алгоритма основной задачи имеет вид:
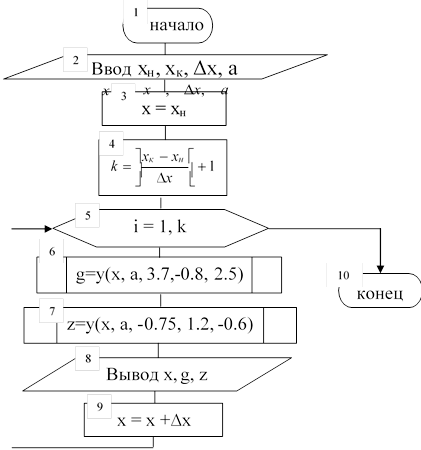
102
Любая программа на языке программирования Pascal может содержать несколько процедур (PROCEDURE) и функций (FUNCTION). Процедуры и функции объявляются в разделе описания за разделом переменных. Пример структуры программы с двумя подпрограммами имеет вид:
Program имя программы; Label ..;
Const...;
Type.... ;
Var. ;
Подпрограмма Р1; Подпрограмма Р2; Begin
Операторы;
Обращение к подпрограмме Р1; Операторы;
Обращение к подпрограмме Р1; Операторы;
Обращение к подпрограмме Р2; Операторы;
Обращение к подпрограмме Р2; Операторы;
End.
Выполнение программы начинается с операторов основной программы. При необходимости вызывается подпрограмма, и начинают выполняться ее операторы. Затем управление передается вновь к основной программе, которая продолжает свое выполнение. Подпрограмма оформляется аналогично основной программе, то есть состоит из заголовка, раздела описаний и раздела операторов.
Структура процедуры имеет вид:
Begin
Оператор 2;
Оператор n
103
В заголовке указывается служебное слово Procedure, за которым следует имя процедуры и формальные параметры в круглых скобках. Раздел описаний процедуры состоит из разделов меток, констант, типов, переменных и, в свою очередь, процедур и функций. Раздел операторов располагается в операторных скобках Begin ... End.
Процедура вызывается при выполнении оператора:
С помощью формальных и фактических параметров данные передаются из программы в процедуру и, наоборот, из процедуры в программу. Каждый формальный параметр указывается вместе со своим типом. Соответствующий ему фактический параметр указывается без типа. Между формальными и фактическими параметрами должно быть соответствие по количеству параметров, по их типу и по порядку следования. Если несколько формальных параметров имеют одинаковый тип, тогда их можно объединить в список, то есть перечислить параметры через запятую, а затем указать тип.
Среди параметров процедуры выделяют параметры-значения и параметры-переменные. Параметры-значения выступают в качестве входящих параметров процедуры. Они могут принимать значения фактических параметров, но не могут передавать свои значения фактическим параметрам. Параметры-переменные выступают в качестве как входящих, так и выходящих параметров процедуры. Они могут принимать значения фактических параметров, изменять их в процедуре и возвращать новые значения фактическим параметрам. Для выделения параметров-переменных перед ними ставится слово Var в списке формальных параметрах.
Если в процедуру нужно передать в качестве параметра не просто одно значение, а массив, то фактическим параметром должно быть имя массива. При этом формальный параметр указывается после слова Var вместе с типом массива. Само же описание массива выполняется в разделе Type основной программы.
Допускается использование процедур без параметров. В этом случае формальные и фактические параметры отсутствуют. В этом случае передача исходных данных в процедуру и выходных данных из процедуры в основную программу осуществляется с помощью глобальных параметров. А именно, исходные данные и выходные данные процедуры описываются как глобальные в разделе
104
переменных основной программы. Оператор вызова процедуры в этом случае будет состоять только из имени процедуры без фактических параметров.
Структура функции имеет вид:
Begin
Оператор 2;
Оператор n;
End;
Формальные параметры функции подчиняются тем же
правилам, что и в процедуре. Результатом функции является одна простая переменная, значение которой присваивается в теле функции имени функции.
Вызывается функция по ее имени с указанием фактических параметров. Вызов функции можно делать непосредственно внутри выражения.
Пример 3. Заданы массивы В(i), Н(j), где i=1..6; j=1..8. Составить подпрограммы для выполнения следующих действий:
- расчет значений элементов массивов по формулам
B(i) = sin(i + 0.5)+ cos(i - 2.9) H(j) = sin(j -1.4)+ cos(j + 3.7)
- определение разницы максимального и минимального элементов массивов.
Решение.
1) Элементы массивов В, Н, вычисляются по общей формуле:
Y ( f ) = sin( f + A)+ cos( f + C), где f изменяется от 1 до М. Для каждого
массива можно рассчитать элементы, если подставить соответствующие коэффициенты в эту формулу. Например, для массива В индекс f будет изменяется от 1 до 6, то есть М = 6, а коэффициенты А = 0.5 и С = -2.9.
Вычисления элементов массива Y(М) можно оформить в виде отдельной процедуры с именем Dan. Исходными данными для процедуры будут параметры А, С вещественного типа и размерность массива М целого типа. Результатом выполнения процедуры Dan
105
будет массив Y, тип которого описывается в разделе типов основной программы. Индекс массива f будет вспомогательной переменной в процедуре при организации цикла, поэтому описывается как локальная переменная в разделе описаний процедуры.
Процедура Dan имеет вид:
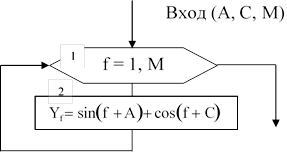Выход (Y)
Procedure Dan (A,C: real; M: integer; Var Y: mas); Var f: integer;
Begin
For f:=1 to M do Y[f]:=sin(f+A)+cos(f+C); End;
2) Для вывода элементов массива Y(М) можно оформить процедуру Vuvod. Исходными данными для процедуры будут размерность массива М целого типа, массив Y типа mas, символьная переменная Z для указания имени массива при печати. Результатом выполнения процедуры Vuvod будет печать элементов массива Y.
Процедура Vuvod имеет вид:
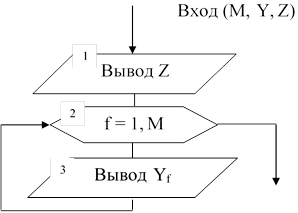Выход (Y)
Procedure Vuvod (M: integer; Y: mas; Z: char); Var f: integer;
Begin
Writeln(„Массив ‟, Z);
For f:=1 to M do Write(Y[f]:6:2, „ „); Writeln; End;
106
3) Определение разницы максимального и минимального элементов массива Y(М) можно оформить в виде отдельной процедуры с именем Ras. Исходными данными для процедуры Ras будет размерность массива М целого типа и массив Y типа mas. Результатом выполнения процедуры Ras будет переменная R действительного типа (разница между максимальным и минимальным элементом массива). Индекс массива f, переменная max (значение максимального элемента) и переменная min (значение минимального элемента) будут вспомогательными в процедуре и описываются как локальные переменные в разделе описаний процедуры.
Процедура Ras имеет вид:
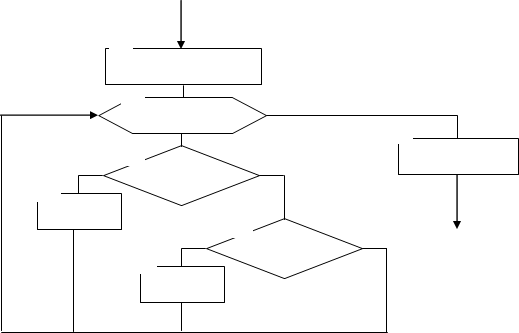Вход
(M, Y)
1
max=Y1 ; min=Y1
2
да 3
4
f = 2, M
Yf >max
7
нет
max=Yf да
6
5
Yf <min
нет
Выход (R)
Procedure Ras (M: integer; Y: mas; Var R: real); Var f: integer; max, min: real;
Begin
max:=Y[1]; min:=Y[1]; For f:=2 to M do
If Y[f]>max then max:=Y[f]
Else If Y[f]< min then min:=Y[f]; R:=max-min;
End;
107
4) В основной программе принимаются следующие обозначения:
NB, NH - размерности массивов В, Н соответственно;
RB, RH - разница между максимальным и минимальным элементов массивов В, Н соответственно.
Схема алгоритма основной задачи имеет вид
 |
Program primer;
Type mas=array[1..50] of real;
Var В, Н: mas; NB, NH: integer; RB, RH: real;
(* Процедура Dan *)
Procedure Dan (A,C: real; M: integer; Var Y: mas); Var f: integer;
Begin
For f:=1 to M do Y[f]:=sin(f+A)+cos(f+C);
End;
108
(* Процедура Ras *)
Procedure Ras (M: integer; Y: mas; Var R: real); Var f: integer; max, min: real;
Begin
max:=Y[1]; min:=Y[1]; For f:=2 to M do
If Y[f]>max then max:=Y[f] Else If Y[f]< min then min:=Y[f]; R:=max-min;
End;
(* Процедура Vuvod *)
Procedure Vuvod (M: integer; Y: mas; Z: char); Var f: integer;
Begin
Writeln(„Массив ‟, Z);
For f:=1 to M do Write(Y[f]:5:3, „ „); Writeln;
End;
(* Основная программа *)
Begin
Write („Ввести размерность массива B‟); Readln(NB);
Dan (0.5,-2.9,NB, B); Ras (NB, B, RB); Vuvod (NB, B, „B‟);
Write („Ввести размерность массива H‟); Readln(NH);
Dan (-1.4,3.7,NH, H); Ras (NH, H, RH); Vuvod (NH, H, „H‟); Writeln („RB=‟, RB:5:3,„ RH=‟, RH:5:3);
End.
В данном примере можно использовать функцию пользователя. Процедуры Dan и Vuvod представить в виде функции нельзя, поскольку в них в качестве данных используется массив Y структурированного типа, а результатом функции может быть только простая переменная. Процедуру Ras можно оформить в виде функции, поскольку выходной величиной является переменная R действительного типа. Этот результат можно присвоить имени функции.
109
Задание
1. Изучить лекционный материал и методические рекомендации для выполнения задания.
2. Разработать алгоритм подпрограмм и алгоритм основной задачи.
3. Составить программу на алгоритмическом языке Pascal.
4. Выполнить отладку и тестирование программы на компьютере.
5. Подготовить отчет о выполнении задания. Пример оформления отчета представлен в приложении 2.
6. Подготовить ответы на контрольные вопросы.
Варианты заданий
|
№ п/п |
Вид задания |
|
1 |
Составить таблицу значений функций y(x) = 3,5logx+2 x +1 и log 2 (x + 2) x g(x) = a log2x (x + 1) на отрезке [1.2;3.6], где Dх=0.4. Для a 2 + log2 x x+3 вычисления log n = ln n использовать подпрограмму – k ln k функцию. |
|
2 |
Составить таблицы значений функций z(x) = 3,4 + logx (x + 2) и 4logx+1 x g(x) = 5,9 - logx2 (x +1) , где 2≤х≤10, Δх=1.5. Для вычисления 2,8logx+1 x log n = ln n использовать подпрограмму – функцию. k ln k |
|
3 |
Вычислить с использованием подпрограммы – функции выражение A = chxshx + 1 ch(x + y)sh(x + y)- 1 ch 2 (x2 + y2 )sh2 (x2 + y2 ), где a b ex + e-x ex - e-x chx = , shx = . Исходные данные: 0≤х≤1, Δх=0.1, 2 2 1≤y≤3, Δy=0.2 |
110
|
4 |
Сформировать массивы чисел a = 2,8(k - 3,6)2 + k + 2, k b = 5,4(j+ 2,6)2 + j+ 2 , где j=1..n, k=1..m с использованием j подпрограммы - функции. |
|
5 |
Координатами задана точка А(x0,y0,z0) и еще 5 точек: А1(x1,y1,z1), А2(x2,y2,z2), А3(x3,y3,z3), А4(x4,y4,z4), А5(x5,y5,z5). Определить среди них точку, которая расположена ближе к точке А(x0,y0,z0). Для определения расстояния между точками использовать подпрограмму - функцию. |
|
6 |
( ) a + 2ln 2 (x + 2,5) Составить таблицы значений функций f x = 3,6 - 3ln 2 (x + 0,8) и ( ) 8,2 + 3,6ln 2 (x + 0,7) g x = , где -5≤х≤10, Δх=1.5 с использованием 2,8 - 2,4a ln 2 (x +1,4) подпрограммы - функции. Значение переменной а ввести. |
|
7 |
Сформировать массивы чисел n = 2,6 sin k + 3,4 и k 1+ sin k 2 +1,8 3,8 sin i2 + 2,4 mi = , где i=1..b, k=1..а с использованием 4 + 5 sin i + 1,6 подпрограммы - функции. |
|
8 |
Вычислить выражение s = sh2 x + ch 2 y - 2sh(x + y)× ch(x + y) с 1 + ch 2 (x + y) использованием подпрограммы - функции, где ex + e-x ex - e-x chx = , shx = . Исходные данные: 1≤х≤10, 2 2 Δх=1.15, 2≤y≤5, Δy=0.3 |
|
9 |
Координатами заданы 3 точки А(x1,y1), В(x2,y2), С(x3,y3). Если они могут быть вершинами треугольника, то определить его вид: равносторонний, равнобедренный, разносторонний. Для определения длин отрезков использовать подпрограмму - функцию. |
|
10 |
2,8sin(j2 + 2) Сформировать массивы чисел a j = cos2 (j2 + 2)+ 3,6 и ksin(k 2 + 3) bk = 4cos2 (k 2 - 0,6)- 8,2 , где j=1..m, k=1..n с использованием подпрограммы - функции. Значение переменной z ввести. |
111
|
11 |
Вычислить с использованием подпрограммы – функции выражение y = hf (x ) + h ( 2 )+ h 2 ( + ) 2 3 1 2 f x2 3 f x1 x2 , где f (x) = ax x + ln x + b , h = x 2 - x1 . Исходные данные: 1≤а≤8, 2,58c 10 Δа=0.5. Значения переменных b, c, x1, x2 ввести. |
|
12 |
Составить программу определения периметра многоугольника, заданного координатами вершин (x1,y1), (x2,y2), (x3,y3), (x4,y4), (x5,y5), (x6,y6). Для вычисления l = (x - x )2 + (y - y )2 длин отрезков использовать i j i j подпрограмму – функцию. |
|
13 |
Сформировать массивы чисел zi = lg1,4i + tg(i -1,8) и lk = lg 0,6k + tg(k + 2,4), где i=1..u, k=1..v с использованием подпрограммы - функции. |
|
14 |
Составить таблицы значений функций p(x) = 15,8x 4 + 1 1 + 2x 2 + 3x 4 и r(x) = 2(a sin2 x + 1+ 2sin x + 3sin2 x ), a где 1≤х≤10, Δх=1.5 с использованием подпрограммы - функции. Значение переменной а ввести. |
|
15 |
Вычислить с использованием подпрограммы – функции shx sh2 (x + y) выражение Q = ch 2 y + 2,8 ch(x + y)+ 1 , где ex + e-x ex - e-x chx = , shx = . Исходные данные: 0.2≤x≤5, 2 2 Δx=0.4, 1≤y≤3, Δy=0.5. |
|
16 |
Составить таблицы значений функций ( ) 2,1x + x 2a t x = и r(x) = 2,8 - 1+ 2e2x + 3e4x , где 1 + 1 + 2 cos 2 x + 3cos 4 x 0.1≤х≤1.1, Δх=0.2 с использованием подпрограммы - функции. |
|
17 |
( ) sin x + 2,8 2 Составить таблицы значений функций g x = 1+ ex+1 и ( ) sin x - 3,6 2 t x = , где 0.1≤х≤1.4, Δх=0.5 с использованием 1+ e2x подпрограммы - функции. |
112
|
18 |
Сформировать массивы чисел x = 1,5i2 - 6,9sin(i -1)+ 8,2 и i z = 2,3k2 + 8,1sin(k + 2)- 3,4 , где i=1..p, k=1..h с использованием k подпрограммы - функции. |
|
19 |
Составить таблицы значений функций Q(x) = e-2x + 3 sin x + 2,8 и P(x) = ex+1 + 3 sin x - 0,4 , где 0.2≤х≤1.6, Δх=0.3 с использованием подпрограммы - функции. |
|
20 |
Координатами задана точка А(x0,y0,z0) и еще 4 точки: А1(x1,y1,z1), А2(x2,y2,z2), А3(x3,y3,z3), А4(x4,y4,z4). Определить среди них точку, которая наиболее удалена от точки А(x0,y0,z0). Для определения расстояния между точками использовать подпрограмму - функцию. |
|
21 |
Составить таблицы значений функций y(x) = logx+1 x + 2 и 4 + log 2 (x + 1) x g(x) = 4,6 - log2x+1 x , где 1≤х≤5, Δх=0.8 с использованием подпрограммы - функции. |
|
22 |
Сформировать массивы чисел x = 3,7 sin3(i + 0,8)- 3 i и i z = 4,2sin3 (k - 0,2)+ 3 k +1 , где i=1..r, k=1..j с использованием k подпрограммы - функции. |
|
23 |
Составить таблицы значений функций S(x) = 1,5cos3 x + 2 3 1+ sin 2 x и t(x) = 2,6cos3 x + 1 3 1- sin 2 x , где 3 7 0.2≤х≤1.4, Δх=0.3 с использованием подпрограммы - функции. |
|
24 |
Сформировать массивы чисел x = 1,4k - e0,5k (2,8 + k) и k y = 3,6m -e0,5m (4,2 + m), где m=1..v, k=1..u с использованием m подпрограммы - функции. |
|
25 |
Составить таблицы значений функций t(x) = cos2 x - 3 1+ ln 2 x и p(x) = 2 cos 2 x - 1 3 1 + ln 2 x , где 0.8≤х≤2.4, Δх=0.3 с 3 использованием подпрограммы - функции. |
|
26 |
Составить таблицы значений функций t = 4,8sin(k + 2,6)- 1 3 k 2 + 1 и w = 3,6sin(i + 0,8)- 1 3 i2 +1 , где k 7 i 7 i=1..d, k=1..p с использованием подпрограммы - функции. |
113
|
27 |
( ) 3,2 - logx (x + 1) 2 Составить таблицы значений функций y x = log (x + 2) и x+1 g(x) = 1+ log2 (x + 3) , где 2≤х≤12, Δх=1.5 с использованием x подпрограммы - функции. |
|
28 |
Вычислить с использованием подпрограммы – функции выражение B = f (x )+ 1 2 ( + )- 3 ( 2 ) ( ) = sin x + e 2x 1 3 f x1 x 2 f x 2 , где f x 2,6a +1 . Исходные данные: 1≤а≤5, Δа=0.5. Значение переменных x1, x2 ввести. |
|
29 |
Сформировать массивы чисел z =1,2(k2 - 2)sin k + 5 k +1 и k y = 3,6(m2 + 3)sin m + 3 m +1 , где m=1..v, k=1..u с использованием m подпрограммы - функции. |
|
30 |
Составить таблицы значений функций Q(x) = e-2x + 3 sin x2 + 0,8 и P(x) = ex+1 + 3 sin x2 - 0,12 , где 0.6≤х≤1.8, Δх=0.1 с использованием подпрограммы - функции. |
Контрольные вопросы
1. Что такое подпрограмма?
2. Какие существуют виды подпрограмм?
3. Какое основное отличие процедуры и функции?
4. Каким образом оформляется подпрограмма? Привести структуру оформления процедуры и функции.
5. Каким образом вызвать процедуру или функцию?
6. Что такое формальные и фактические параметры? Привести примеры их использования.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
