Лабораторная работа

Исследование типовых звеньев САР. Интегрирующее звено

Цель работы: изучение и исследование характеристик интегрирующего звена.

Краткие теоретические сведения

Любая САР состоит из ряда звеньев, каждое из которых обладает определенными динамическими свойствами.

Звеном системы называется ее элемент (часть), обладающий определенными свойствами в динамическом отношении.

В зависимости от характера протекания переходного процесса различают следующие типовые звенья САР:

1. Дифференцирующее звено.

2. Усилительное или безинерционное звено.

3. Интегрирующее звено.

4. Апериодическое звено.

5. Колебательное звено.

6. Звено с чистым запаздыванием.

1) Дифференцирующим звеном называется элемент, у которого скорость изменения выходного сигнала пропорциональна скорости изменения входного сигнала, т.е. пропорциональна первой производной от скорости изменения входного сигнала во времени.

Различают два вида дифференцирующих звеньев: идеальное и реальное.

Дифференциальное уравнение для идеального дифференцирующего звена записывается в виде

, (1)

где К- передаточный коэффициент.

Уравнение в операторной форме при нулевых начальных условиях

Y(p) = KpX(p) (2)

Передаточная функция идеального дифференцирующего звена

W(p) = Kp (3)

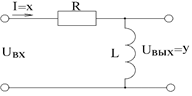
Примером такого звена могла бы служить CR- цепочка, если бы в ней сопротивление R=0 и выходное напряжение снималось бы с этого сопротивления. Идеальное дифференцирующее звено практически осуществить невозможно, поэтому в технике применяются реальные дифференцирующие звенья. Последние обладают инерционностью и в них имеются потери энергии.

Дифференциальное уравнение для реального дифференцирующего звена:

, (4)

где Т- постоянная времени, служащая мерой инерции переходного процесса.

Уравнение в операторной форме при нулевых начальных условиях

(Tp+1)Y(p)=KTpX(p) (5)

Передаточная функция реального дифференцирующего звена

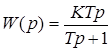(6)

Примерами реальных дифференцирующих звеньев могут служить трансформатор; CR- контур (Рисунок 2), где выходной величиной является напряжение, снимаемое с сопротивления R; цепь с активным сопротивлением и индуктивностью (Рисунок 3), где выходной величиной является напряжение, снимаемое с индуктивности L.

2) Интегрирующим звеном считают такое звено, выходная величина которого пропорциональна интегралу по времени от входной величины.

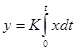(7)

Интегрирующим называется такое звено, у которого скорость изменения выходной величины пропорциональна входной величине и которое описывается дифференциальным уравнением первого порядка.

(8)

Интегрирующее звено иногда называют астатическим.

Преобразовав дифференциальное уравнение интегрирующего звена по Лапласу, получим:

pY(p)=KX(p), (9)

откуда находим передаточную функцию интегрирующего звена

(10)

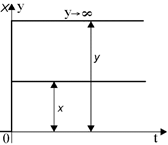
Если входная и выходная величины имеют одинаковую размерность, то коэффициент К имеет размерность . В этом случае дифференциальное уравнение удобнее записывать в виде

, (11)

где Т=1/К.

При этом передаточная функция звена примет вид:

(12)

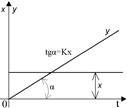
Величина Т называется постоянной времени интегрирующего звена.

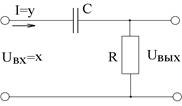
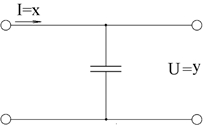Примером интегрирующего звена служит двигатель вращения, у которого угол поворота выходного вала пропорционален входному сигналу, например напряжению на якоре ДПТ; конденсатор, заряжаемый током (Рисунок 5). Интегрирующее звено обладает «памятью». Например, конденсатор, зарядившись, входным током, хранит свой заряд.

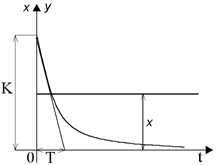
3) В апериодическом звене выходная величина при входном единичном скачкообразном воздействии изменяется по экспоненциальному закону, стремясь к определенному предельному значению. Выходной сигнал звена запаздывает по отношению к входному.

Переходная характеристика апериодического звена описывается дифференциальным уравнением

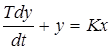, (13)

где Т- постоянная времени звена.

Запишем дифференциальное уравнение в операторной форме

TpY(p)+Y(p)=KX(p), (14)

откуда передаточная функция апериодического звена

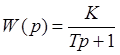(15)

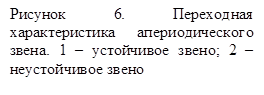
Апериодическое звено образуется из элемента, накапливающего энергию (например, индуктивность, емкость), и элемента, рассеивающего эту энергию (например, электрическое сопротивление). Различают устойчивое (кривая 1 рисунок 6) и неустойчивое (кривая 2 рисунок 6) апериодические звенья.

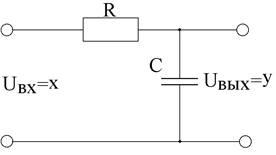
Примером таких звеньев могут быть инерционные датчики (термопары x®, у®термоЭДС), магнитные усилители, пассивные четырехполюсники RC (Рисунок 7).

Оборудование: лабораторный стенд, соединительные провода, осциллограф.

Задание 1: исследование реакции интегрирующего звена на передний фронт импульса.

Порядок выполнения работы

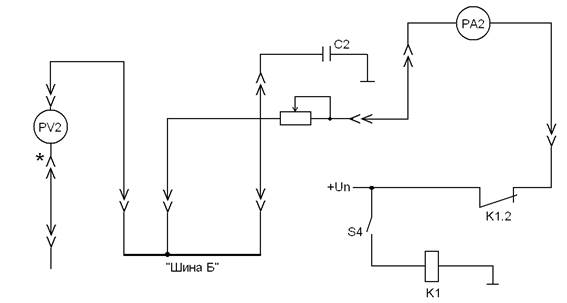
1. Ознакомиться с электрической схемой опыта (Рисунок 8).

2. Соединить гнездо контакта реле К1.2 к гнезду “10” миллиамперметра РА2.

3. От гнезда “*” того же миллиамперметра РА2 произвести соединение с гнездом переменного резистора R14.

4. Второй вывод резистора R14 соединить с шиной “6”.

5. От шины “6” сделать два ответвления: одно на гнездо “20” вольтметра PV2, другое на гнездо конденсатора С2.

6. Второе гнездо “*” вольтметра PV2 соединить с нулевым проводом стенда.

7. Собрать схему секундомера. Для этого соединить гнезда “X1”-“X4” шины, идущей от секундомера с соответствующими входными гнездами микросхем дешифратора D11, D12.

8. Установить ручку регулятора R14 в крайне правое положение.

9. Установить переключатель S4 в положение “I”.

10. Выключатель “разрешение” на счетчике должен находиться в нижнем положении.

11. Включить лабораторный стенд.

12. Тумблером “+5B” включить счетчик. При этом должны загореться все три разряда индикатора.

13. При необходимости обнулить счетчик кнопкой “сброс”.

14. Одновременно перевести переключатели S4 и “разрешение” в положение, противоположное исходному. При этом произойдет включение счета счетчика и начнется заряд конденсатора С2 через нормальнозамкнутые контакты реле К1.2.

15. Снять показания вольтметра PV2, миллиамперметра РА2, следя за увеличивающимся счетом счетчика. Показания приборов занести в таблицу 1.

Таблица 1

№ опыта	1	2	3	4	5	6	7	8	9	10	11
t, с	0,05	1	2	3	4	5	6	7	8	9	10
U_вх, В
I_вх, А
U_вых, В

16. В случае если требуется повторить опыт, необходимо остановить и сбросить счетчик, разрядить конденсатор. Для этого вынуть соединительный провод, идущий к конденсатору С2 из гнезда шины “6” и на несколько секунд подсоединить его к нулевому проводу стенда.

17. По формуле

U_вых=U_вх·(1-e^(-^a^·^t⁾), (16)

где e- основание натурального логарифма (принять равным 2,71),

а- произведение R·C (R принять равным 1 кОм, С принять равным 0,000001Фарада (1000мкФ)

найти напряжение на конденсаторе в любой момент времени заряда t.

18. На основании вычислений заполнить таблицу 1.

19. На основании полученных результатов построить графики зависимости: U_вых=f(t) и I_вх=f(t).

Задание 2: Исследование реакции интегрирующего звена на задний фронт импульса.

Порядок выполнения работы

На основе собранной схемы первого задания выполнить следующее:

- Выключить тумблер “разрешение” счетчика и обнулить его.

- Произвести полную зарядку конденсатора и выполнить следующие переключения:

1. Поставить переключатель S4 в положение “I”.

2. Поменять местами провода на входных гнездах миллиамперметра РА2.

3. Вынуть соединительный проводник из гнезда контакта реле К1.2 и подсоединить его к нулевому проводнику стенда, одновременно включив тумблер “Разрешение” счетчика.

4. Снять показания вольтметра PV2, миллиамперметра РА2, следя за увеличивающимся счетом счетчика Показания приборов занести в таблицу 2

Таблица 2

№ опыта	1	2	3	4	5	6	7	8	9	10	11
t, с	0,05	1	2	3	4	5	6	7	8	9	10
U_вх, В
I_вх, А
U_вых, В

5. На основании полученных результатов построить графики зависимости: U_вых=f(t) и I_вх=f(t).

Контрольные вопросы

1. Назвать основные виды типовых динамических звеньев.

2. Что называется переходной характеристикой?

3. По каким признакам классифицируются динамические звенья?

4. Привести примеры интегрирующих звеньев.

Скачано с www.znanio.ru