Лекция № 4: Измерение информации. Единицы измерения информации.

Цели занятия: изучить основные единицы измерения информации, алфавитный подход к измерению информации.

Задачи занятия:

Обучающие: закрепить знания об информации, ее свойствах, единицах измерения информации и информационных процессах; закрепить навыки решения задач по теме «Алфавитный подход к определению количества информации».

Развивающие: развивать технические способности студентов; активировать мыслительную деятельность студентов; развивать умение конспектировать; способствовать развитию умений планировать свою деятельность, применять полученные знания в измененной ситуации.

Воспитательные: воспитание информационной культуры обучающихся, внимательности, аккуратности, дисциплинированности, усидчивости.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.              Босова Л. Л., Босова А. Ю.. Информатика. Базовый уровень: учебник для 10 класса — М.: БИНОМ. Лаборатория знаний, 2017

2.              Семакин И.Г. Информатика: учебник для 10 кл. / И.Г. Семакин, Е.К. Хеннер, Шеина Т.Ю.– М.: Изд-во "БИНОМ. Лаборатория знаний", 2015. – 264с.

3.              Цифровое неравенство // Наука и жизнь. URL: https://www.nkj.ru/archive/articles/6053/ (дата обращения: 19.07.2018).

4.              Видеоуроки по теме лекции: Измерение информации Объемный подход| Информатика 10-11 класс| Инфоурок- https://www.youtube.com/watch?v=EzOORcAjnBc

План

1.      Измерение информации. Количество информации как мера уменьшения неопределенности знаний. Алфавитный подход к определению количества информации.

2.      Содержательный (вероятностный) подход к измерению информации.

1. Измерение информации. Количество информации как мера уменьшения неопределенности знаний. Алфавитный подход к определению количества информации

Вопрос об измерении количества информации является очень важным как для науки, так и для практики. В самом деле, если информация является предметом нашей деятельности, мы ее храним, передаем, принимаем, обрабатываем. Поэтому важно договориться о способе ее измерения, позволяющем, например, ответить на вопросы: достаточно ли места на носителе, чтобы разместить нужную нам информацию, или сколько времени потребуется, чтобы передать ее по имеющемуся каналу связи. Величина, которая нас в этих ситуациях интересует, называется объемом информации. В таком случае говорят об алфавитном, или объемном, подходе к измерению информации.

Алфавитный подход к измерению информации применяется в цифровых

(компьютерных) системах хранения и передачи информации. В этих системах используется двоичный способ кодирования информации. При алфавитном подходе для определения количества информации имеет значение лишь размер (объем)  хранимого  и  передаваемого  кода. Алфавитный  подход еще называют объемным подходом. Из курса информатики 7-9 классов вы знаете, что если с помощью i-разрядного двоичного кода можно закодировать алфавит, состоящий из N символов (где N — целая степень двойки), то эти величины связаны между собой по формуле:

2ⁱ = N. Число N называется мощностью алфавита.

Если, например, i = 2, то можно построить 4 двухразрядные комбинации из нулей и единиц, т. е. закодировать 4 символа. При i = 3 существует 8 трехразрядных комбинаций нулей и единиц (кодируется 8 символов):

Английский алфавит содержит 26 букв. Для записи текста нужны еще как минимум шесть символов: пробел, точка, запятая, вопросительный знак, восклицательный знак, тире. В сумме получается расширенный алфавит мощностью в 32 символа.

Поскольку 32 = 2⁵, все символы можно закодировать всевозможными пятиразрядными двоичными кодами от 00000 до 11111. Именно пятиразрядный код использовался в телеграфных аппаратах, появившихся еще в XIX веке. Телеграфный аппарат при вводе переводил английский текст в двоичный код, длина которого в 5 раз больше, чем длина исходного текста.

В двоичном коде каждая двоичная цифра несет одну единицу

информации, которая называется 1 бит.

Бит является основной единицей измерения информации.

Длина двоичного кода, с помощью которого кодируется символ алфавита, называется информационным весом символа. В рассмотренном выше примере информационный вес символа расширенного английского алфавита оказался равным 5 битам.

Информационный объем текста складывается из информационных весов всех составляющих текст символов. Например, английский текст из 1000 символов в телеграфном сообщении будет иметь информационный объем 5000 битов.

Алфавит русского языка включает 33 буквы. Если к нему добавить еще пробел и пять знаков препинания, то получится набор из 39 символов. Для двоичного кодирования символов такого алфавита пятиразрядного кода уже недостаточно. Нужен как минимум 6-разрядный код. Поскольку 2⁶ = 64, остается еще резерв для 25 символов (64 - 39 = 25). Его можно использовать для кодирования цифр, всевозможных скобок, знаков математических операций и других  символов,  встречающихся  в  русском  тексте.  Следовательно, информационный вес символа в расширенном русском алфавите будет равен 6 битам. А текст из 1000 символов будет иметь объем 6000 битов.

Итак, если i — информационный вес символа алфавита, а К — количество символов в тексте, записанном с помощью этого алфавита, то информационный объем I текста выражается формулой:

I = К x i (битов).

Идея измерения количества информации в сообщении через

длину двоичного кода этого сообщения принадлежит выдающемуся российскому математику Андрею Николаевичу Колмогорову. Согласно Колмогорову, количество информации, содержащееся в тексте, определяется минимально возможной длиной двоичного кода, необходимого для представления этого текста.

Для определения информационного веса символа полезно знать ряд целых степеней двойки. Вот как он выглядит в диапазоне от 2¹ до 2¹⁰:

Поскольку мощность N алфавита может не являться целой степенью двойки, информационный вес символа алфавита мощности N определяется следующим образом. Находится ближайшее к N значение во второй строке таблицы, не меньшее чем N.

Соответствующее значение i в первой строке будет равно информационному весу символа.

Пример. Определим информационный вес символа алфавита, включающего в себя все строчные и прописные русские буквы (66); цифры (10); знаки препинания, скобки, кавычки (10). Всего получается 86 символов.

Поскольку 2⁶ < 86 < 2⁷, информационный вес символов данного алфавита равен 7 битам. Это означает, что все 86 символов можно закодировать семиразрядными двоичными кодами.

Для двоичного представления текстов в компьютере чаще всего применяется восьмиразрядный код. С помощью восьмиразрядного кода можно закодировать алфавит из 256 символов, поскольку 256 = 2⁸. В стандартную кодовую таблицу (например, используемую в ОС Windows таблицу ANSI) помещаются все необходимые символы: английские и русские буквы — прописные и строчные, цифры, знаки препинания, знаки арифметических операций, всевозможные скобки и пр.

 Более крупной, чем бит, единицей измерения информации является

байт: 1 байт = 8 битов.

Информационный объем текста в памяти компьютера измеряется в

байтах. Он равен количеству символов в записи текста.

Одна страница текста на листе формата А4 кегля 12 с одинарным интервалом между строками в компьютерном представлении будет иметь объем 4000 байтов, так как на ней помещается примерно 4000 знаков.

Помимо бита и байта, для измерения информации используются и более крупные единицы:

1 Кб (килобайт) = 2¹⁰ байтов = 1024 байта;

1 Мб (мегабайт) = 2¹⁰ Кб = 1024 Кб;

1 Гб (гигабайт) = 2¹⁰ Мб = 1024 Мб; 1 Тб (терабайт) = 2¹⁰ Гб = 1024 Гб.

Объем той же страницы текста будет равен приблизительно 3,9 Кб. А книга из 500 таких страниц займет в памяти компьютера примерно 1,9 Мб.

                   В     компьютере     любые      виды     информации:      тексты,      числа,

изображения, звуки — представляются в форме двоичного кода.

Объем информации любого вида, выраженный в битах, равен длине

двоичного кода, в котором эта информация представлена.

Алфавит – это вся совокупность символов, используемых в некотором языке для представления информации. Каждый алфавит обладает особой характеристикой – мощностью.

Мощность алфавита (N) – это полное число символов в алфавите. При алфавитном подходе считается, что каждый символ текста имеет определённый «информационный вес». Обозначение: i. Информационный вес символа зависит от мощности алфавита! Наименьшее количество символов имеется в двоичном алфавите. Он содержит всего два символа, которые обозначаются «0» и «1».

Информационный вес символа двоичного алфавита принят за эталонную единицу информации и называется 1 бит.

2. Содержательный (вероятностный) подход к измерению информации Неопределенность знания и количество информации

Содержательный подход к измерению информации отталкивается от определения информации как содержания сообщения, получаемого человеком. Сущность содержательного подхода заключается в следующем: сообщение, информирующее об исходе какого-то события, снимает неопределенность знания человека об этом событии.

Чем больше первоначальная неопределенность знания, тем больше информации несет сообщение, снимающее эту неопределенность.

Приведем примеры, иллюстрирующие данное утверждение.

Ситуация 1. В ваш класс назначен новый учитель информатики; на вопрос «Это мужчина или женщина?» вам ответили: «Мужчина».

Ситуация 2. На чемпионате страны по футболу играли команды «Динамо» и «Зенит». Из спортивных новостей по радио вы узнаете, что игра закончилась победой «Зенита».

Ситуация 3. На выборах мэра города было представлено четыре кандидата.

После подведения итогов голосования вы узнали, что избран Н. Н. Никитин.

Вопрос: в какой из трех ситуаций полученное сообщение несет больше информации?

 Неопределенность знания — это количество возможных вариантов ответа на интересовавший вас вопрос. Еще можно сказать: возможных исходов события. Здесь событие — например, выборы мэра; исход — выбор, например, Н. Н. Никитина.

В первой ситуации 2 варианта ответа: мужчина, женщина; во второй ситуации 3  варианта:  выиграл «Зенит», ничья,  выиграло «Динамо»; в третьей ситуации — 4 варианта: 4 кандидата на пост мэра.

Согласно данному выше определению, наибольшее количество информации несет сообщение в третьей ситуации, поскольку неопределенность знания об исходе события в этом случае была

наибольшей.

В 40-х годах XX века проблема измерения информации была решена американским ученым Клодом Шенноном — основателем теории информации. Согласно Шеннону, информация — это снятая неопределенность знания человека об исходе какого-то события.

В теории информации единица измерения информации определяется следующим образом.

Сообщение, уменьшающее неопределенность знания об исходе

некоторого события в два раза, несет 1 бит информации.

Согласно этому определению, сообщение в первой из описанных ситуаций несет 1 бит информации, поскольку из двух возможных вариантов ответа был выбран один.

Следовательно, количество информации, полученное во второй и в третьей ситуациях, больше, чем один бит. Но как измерить это количество?

Рассмотрим еще один пример.

Ученик написал контрольную по информатике и спрашивает учителя о полученной оценке. Оценка может оказаться любой: от 2 до 5. На что учитель отвечает: «Угадай оценку за два вопроса, ответом на которые может быть только "да" или "нет"». Подумав, ученик задал первый вопрос: «Оценка выше тройки?». «Да», — ответил учитель. Второй вопрос: «Это пятерка?». «Нет», — ответил учитель. Ученик понял, что он получил четверку. Какая бы ни была оценка, таким способом она будет угадана!

Первоначально неопределенность знания (количество возможных оценок) была равна четырем. С ответом на каждый вопрос неопределенность знания уменьшалась в 2 раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.

Узнав оценку (одну из четырех возможных), ученик получил 2 бита информации.

Рассмотрим еще один частный пример, а затем выведем общее правило.

Вы едете на электропоезде, в котором 8 вагонов, а на вокзале вас встречает товарищ. Товарищ позвонил вам по мобильному телефону и спросил, в каком вагоне  вы  едете.  Вы  предлагаете  угадать  номер  вагона,  задав  наименьшее количество вопросов, ответами на которые могут быть только слова «да» или «нет».

Немного подумав, товарищ стал спрашивать:

— Номер вагона больше четырех?

— Да.

— Номер вагона больше шести?

— Нет.

— Это шестой вагон?

— Нет.

— Ну теперь все ясно! Ты едешь в пятом вагоне!

Схематически поиск номера вагона выглядит так:

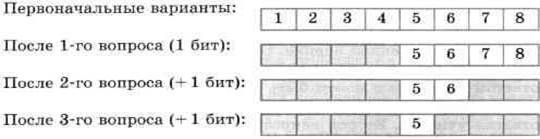
Каждый ответ уменьшал неопределенность знания в два раза. Всего было задано три вопроса. Значит, в сумме набрано 3 бита информации. То есть сообщение о том, что вы едете в пятом вагоне, несет 3 бита информации.

Способ решения проблемы, примененный в примерах с оценками и вагонами, называется методом половинного деления: ответ на каждый вопрос уменьшает неопределенность знания, имеющуюся перед ответом на этот вопрос, наполовину. Каждый такой ответ несет 1 бит информации.

Заметим, что решение подобных проблем методом половинного деления наиболее рационально. Таким способом всегда можно угадать, например, любой из восьми вариантов за 3 вопроса. Если бы поиск производился последовательным перебором: «Ты едешь в первом вагоне?» «Нет», «Во втором вагоне?» «Нет» и т. д., то про пятый вагон вы смогли бы узнать после пяти вопросов, а про восьмой — после восьми.

«Главная формула» информатики

Сформулируем одно очень важное условие, относящееся к рассмотренным примерам. Во всех ситуациях предполагается, что все возможные исходы события равновероятны. Равновероятно, что учитель может быть мужчиной или женщиной; равновероятен любой исход футбольного матча, равновероятен выбор одного из четырех кандидатов в мэры города. То же относится и к примерам с оценками и вагонами.

Тогда полученные нами результаты описываются следующими формулировками:

•                  сообщение об одном из двух равновероятных исходов некоторого события несет 1 бит информации;

•                  сообщение об одном из четырех равновероятных исходов некоторого события несет 2 бита информации;

•                  сообщение об одном из восьми равновероятных исходов некоторого события несет 3 бита информации.

Обозначим буквой N количество возможных исходов события, или, как мы это еще называли, — неопределенность знания. Буквой i будем обозначать количество информации в сообщении об одном из N результатов. В примере с учителем: N = 2, i = 1 бит; в примере с оценками: N = 4, i = 2 бита; в примере с вагонами: N = 8, i = 3 бита.

Нетрудно заметить, что связь между этими величинами выражается следующей формулой:

2ⁱ = N.

Действительно: 2¹ = 2 ; 2² = 4 ; 2³ = 8.

С полученной формулой вы уже знакомы из курса информатики для 7 класса и еще не однажды с ней встретитесь. Значение этой формулы столь велико, что мы назвали ее главной формулой информатики. Если величина N известна, a i неизвестно, то данная формула становится уравнением для определения i. В математике такое уравнение называется показательным уравнением.

Пример. Вернемся к рассмотренному выше примеру с вагонами. Пусть в поезде не 8, а 16 вагонов. Чтобы ответить на вопрос, какое количество информации содержится в сообщении о номере искомого вагона, нужно решить уравнение:

2ⁱ = 16.

Поскольку 16 = 2⁴ , то i = 4 бита.

Количество информации i, содержащееся в сообщении об одном из N равновероятных исходов некоторого события, определяется из решения показательного уравнения:

2ⁱ = N.

Пример. В кинозале 16 рядов, в каждом ряду 32 места. Какое количество информации несет сообщение о том, что вам купили билет на 12-й ряд, 10-е место? Решение задачи: в кинозале всего 16 • 32 = 512 мест. Сообщение о купленном билете однозначно определяет выбор одного из этих мест. Из уравнения 2ⁱ = 512 = 2⁹ получаем: i - 9 битов.

Но эту же задачу можно решать иначе. Сообщение о номере ряда несет 4 бита информации, так как 2⁴ = 16. Сообщение о номере места несет 5 битов информации, так как 2⁵ = 32. В целом сообщение про ряд и место несет: 4 + 5 = 9 битов информации.

Данный пример иллюстрирует выполнение закона аддитивности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.

Сделаем одно важное замечание. С формулой 2ⁱ = N мы уже встречались, обсуждая алфавитный подход к измерению информации (см. § 3. Измерение информации. Алфавитный подход). В этом случае N рассматривалось как мощность алфавита, а i — как информационный вес каждого символа алфавита. Если допустить, что все символы алфавита появляются в тексте с одинаковой частотой, т. е. равновероятно, то информационный вес символа i тождественен количеству информации в сообщении о появлении любого символа в тексте. При этом N — неопределенность знания о том, какой именно символ алфавита должен стоять в данной позиции текста. Данный факт демонстрирует связь между алфавитным и содержательным подходами к измерению информации.

Формула Хартли

Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему равно количество информации в сообщении о результате матча «Динамо»-

«Зенит»? В этой ситуации N = 3. Можно догадаться, что решение уравнения

2ⁱ = 3. будет дробным числом, лежащим между 1 и 2, поскольку 2¹ = 2 < 3, а 2² = 4 >

3. А как точнее узнать это число?

В математике существует функция, с помощью которой решается показательное уравнение. Эта функция называется логарифмом, и решение нашего уравнения записывается следующим образом:

i = log₂ N.

Читается это так: «логарифм от N по основанию 2». Смысл очень простой: логарифм по основанию 2 от А — это степень, в которую нужно возвести 2, чтобы получить N. Например, вычисление уже известных вам значений можно представить так:

log₂ 2 = 1, log₂ 4 = 2, log₂ 8 = 3.

Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор. Определим количество информации, полученной из сообщения об одном исходе события из трех равновероятных, с помощью электронной таблицы. На рисунке 4 представлены два режима электронной таблицы: режим отображения формул и режим отображения значений.

Рис.4. Определение количества информации в электронных таблицах с помощью функции логарифма

В табличном процессоре Microsoft Excel функция логарифма имеет следующий вид: LOG(apryмент; основание). Аргумент — значение N находится в ячейке А2, а основание логарифма равно 2. В результате получаем с точностью до девяти знаков после запятой: i = log23 = 1,584962501 (бита).

Формула для измерения количества информации: i = log2N была предложена американским ученым Ральфом Хартли — одним из основоположников теории информации.

Формула Хартли: i = log₂ N

Здесь i — количество информации, содержащееся в сообщении об одном из N равновероятных исходов события.

Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, в то время как информационный объем, вычисляемый путем применения алфавитного подхода, может иметь только целочисленное значение.

ДОМАШНЕЕ ЗАДАНИЕ:

1.      Проработать лекционный материал.

2.      Ответить на вопросы.

2.1.           Есть ли связь между алфавитным подходом к измерению информации и содержанием информации?

2.2.           В чем можно измерить объем письменного или печатного текста?

2.3.           Какие единицы используются для измерения объема информации на компьютерных носителях?

2.4.           Сообщение, записанное буквами из 64-символьного алфавита, содержит 100 символов. Какой объем информации оно несет?

2.5.           Сколько символов содержит сообщение, записанное с помощью 16- символьного алфавита, если его объем составляет 1/16 Мб?

2.6.           Сообщение занимает 2 страницы и содержит 1/16 Кб информации. На каждой странице 256 символов. Какова мощность используемого алфавита?

2.7.           Придумайте несколько ситуаций, при которых сообщение несет 1 бит информации.

2.8.           Сколько битов информации несет сообщение о том, что из колоды в 32 карты достали «даму пик»?

2.9.           При угадывании методом половинного деления целого числа из диапазона от 1 до N был получен 1 байт информации. Чему равно N?

2.10.       Проводятся две лотереи: «4 из 32» и «5 из 64». Сообщение о результатах какой из лотерей несет больше информации?