Лекция по теме Алфавитный подход к определению количества информации

Тема 2. Алфавитный подход к определению количества информации Выбор способа представления информации в соответствии с поставленной задачей.

Алфавитный (объёмный) подход к измерению информации позволяет определить количество информации, заключенной в тексте, записанном с помощью некоторого алфавита.

Алфавит - множество используемых символов в языке.

Обычно под алфавитом понимают не только буквы, но и цифры, знаки препинания и пробел.

Мощность алфавита (N) - количество символов, используемых в алфавите.

Например, мощность алфавита из русских букв равна 32 (буква ё обычно не используется).

Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле Хартли:

где N – мощность алфавита.

Формула Хартли задает связь между количеством возможных событий N и количеством информации i:

N=2i

Из базового курса информатики известно, что в компьютерах используется двоичное кодирование информации. Для двоичного представления текстов в компьютере чаще всего используется равномерный восьмиразрядный код. С его помощью можно закодировать алфавит из 256 символов, поскольку 256=28.

В стандартную кодовую таблицу (например, ASCII) помещаются все необходимые символы: английские и русские прописные и строчные буквы, цифры, знаки препинания, знаки арифметических операций, всевозможные скобки и пр.

В двоичном коде один двоичный разряд несет одну единицу информации, которая называется 1 бит.

Например, в 2-символьном алфавите каждый символ «весит» 1 бит (log22=1); в 4-символьном алфавите каждый символ несет 2 бита информации (log24=2); в 8-символьном - 3 бита (log28=3) и т. д.

Один символ из алфавита мощностью 256 (28) несет в тексте 8 битов информации. Такое количество информации называется байтом.

1 байт =8 битов

Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству знаков в записи текста.

Для измерения информации используются и более крупные единицы:

 Таблица 1.

Единицы измерения количества информации, в названии которых есть приставки «кило», «мега» и т. д., с точки зрения теории измерений не являются корректными, поскольку эти приставки используются в метрической системе мер, в которой в качестве множителей кратных единиц используется коэффициент

 10, где n=3,6,9 и т. д.

Для устранения этой некорректности Международная электротехническая комиссия, занимающаяся созданием стандартов для отрасли электронных технологий, утвердила ряд новых приставок для единиц измерения количества информации: 

киби (kibi), 

меби (mebi), 

гиби (gibi), 

теби (tebi), 

пети (peti),   

эксби (exbi).

Однако пока используются старые обозначения единиц измерения количества информации, и требуется время, чтобы новые названия начали широко применяться.

Последовательность действий при переводе одних единиц измерения информации в другие приведена на следующей схеме:

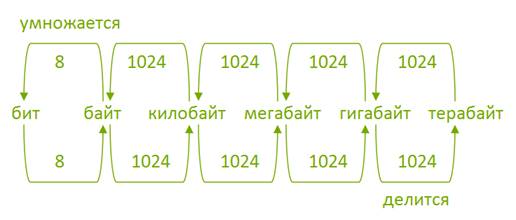
                                                                                                 Рисунок 1.

Если весь текст состоит из K символов, то при алфавитном подходе объём V содержащейся в нем информации равен:

V=K⋅i

где i - информационный вес одного символа в используемом алфавите.

Зная, что i=log2N, данную выше формулу можно представить в другом виде: если количество символов алфавита равно N, а количество символов в записи сообщения - K, то информационный объем V данного сообщения вычисляется по формуле:

V=K⋅log2N

При алфавитном подходе к измерению информации информационный объем текста зависит только от размера текста и от мощности алфавита, а не от содержания. Поэтому нельзя сравнивать информационные объемы текстов, написанных на разных языках, по размеру текста.

Пример:

1. Считая, что каждый символ кодируется одним байтом, оцените информационный объем следующего предложения: Белеет Парус Одинокий В Тумане Моря Голубом!

Решение.

Так как в предложении 44 символа (считая знаки препинания и пробелы), то информационный объем вычисляется по формуле:

V=44⋅1 байт=44 байта=44⋅8 бит=352 бита

2. Объем сообщения равен 11 Кбайт. Сообщение содержит 11264 символа. Какова мощность алфавита?

Решение.

Выясним, какое количество бит выделено на 1 символ. Для этого переведем объем сообщения в биты:

11 Кбайт=11⋅210 байт=11⋅210⋅23 бит=11⋅213 бит и разделим его на число символов.

На 1 символ приходится: 11⋅21311264=11⋅21311⋅210=23=8 бит.

Мощность алфавита определяем из формулы Хартли: N=28=256 символов.

Закрепление изученного материла.

1.Вероятность первого события составляет 0,5, а второго и третье­го — 0,25. Какое количество информации мы получим после реализации одного из них?

2.Какое количество информации получит второй игрок в игре

«Угадай число» при оптимальной стратегии, если первый иг­рок загадал число: от 1 до 64? От 1 до 128?

Скачано с www.znanio.ru