Логарифмические уравнения профильного уровня из материалов ЕГЭ.

Логарифмические уравнения из материалов ЕГЭ профильного уровня.

 (Для всех уравнений делается проверка или находится ОДЗ).

1. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Запишем исходное уравнение в виде:

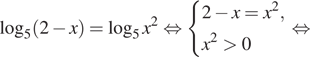
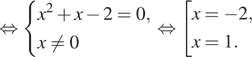
б)  Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

2. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Из уравнения получаем:

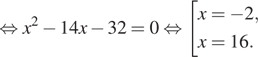
б)  Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

3. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Запишем исходное уравнение в виде:

Значит, откуда или откуда

б)  Заметим, что

Значит, указанному отрезку принадлежит корень 2.

Ответ: а) 2 и б) 2.

Критерии проверки:

Ответ: а) 2 и б) 2.

514623

а) 2 и б) 2.

Источник: Задания 13 (С1) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Вариант 701 (C часть).

Классификатор алгебры: Логарифмические уравнения

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.6 Логарифмические уравнения

4.  а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Заметим, что уравнение определено при любом Запишем исходное уравнение в виде:

Значит, либо откуда или либо откуда или

б)  Поскольку отрезку принадлежат корни и

Ответ: а) б)

Критерии проверки:

Ответ: а) б)

502053

а) б)

Источник: ЕГЭ по математике 10.06.2013. Вторая волна. Центр. Вариант 602., Задания 13 (С1) ЕГЭ 2013

Классификатор алгебры: Логарифмические уравнения, Уравнения высших степеней

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.1 Квадратные уравнения, 2.1.6 Логарифмические уравнения

5.   а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Поскольку получаем:

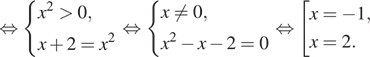
б)  В силу цепочки соотношений заданному отрезку принадлежит только число −1.

Ответ: а) {−1, 2}, б) −1.

6. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие промежутку

Решение. а)  Преобразуем уравнение:

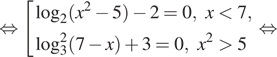
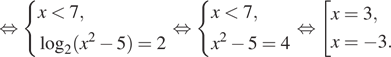
б)  Заметим, что

поэтому в указанный промежуток попадает только корень

Ответ: а) {−3; 3} б) 3.

Критерии проверки:

Ответ: а) {−3; 3} б) 3.

550261

а) {−3; 3} б) 3.

Источник: А. Ларин. Тренировочный вариант № 323. (часть C).

Классификатор алгебры: Логарифмические уравнения, Область определения уравнения, Сравнение чисел

Методы алгебры: Группировка

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.6 Логарифмические уравнения, 2.2.4 Логарифмические неравенства

7. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Заметим, что уравнение имеет смысл при (⁎). Преобразуем его при этих условиях:

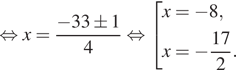
б)  Заметим, что 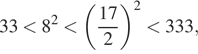поэтому подходят оба корня.

Ответ: а) б)

8.     а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].

Решение. а)  Запишем исходное уравнение в виде:

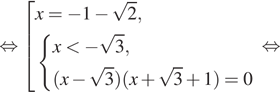
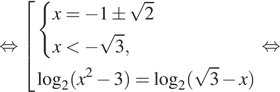
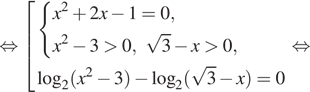
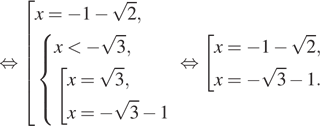
б)  Проверим корни на отрезке :

Поскольку конечное неравенство верное, значение подходит и войдет в ответ.

Проверим следующее значение x:

Так как второе значение не дает правильного конечного неравенства, оно не войдет в ответ.

Ответ: а) б)

Скачано с www.znanio.ru