Логічні вирази та логічні операції

Логічні вирази та логічні операції

Мета: ознайомлення з поняттями про прості та складені умови, навчити записувати умову логічної задачі у вигляді системи логічних виразів, виховання інформаційної культури.

Тип уроку: вивчення нового навчального матеріалу

Обладнання: презентація – супровід уроку.

Хід уроку

І. Організаційний момент

ІІ. Аналіз результатів тематичної контрольної роботи

ІІІ. Актуалізація опорних знань

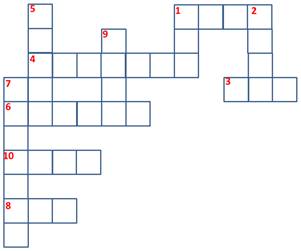
Розв’яжіть кросворд

По горизонталі: 1. Корінь квадратний. 3. Кінець програми. 4. Описувач типу величини. 6. Оператор вводу. 8. Логічна операція «і». 10. Безумовний перехід.

По вертикалі: 1. Стандартна функція. 2. Службове слово. 5. Оператор виводу. 7. Службове слово. 9. Описувач типу величини.

Відповідь:

ІV. Викладання нового матеріалу

1. Логічні  вирази. Обчислення значень логічних виразів

Крім арифметичних виразів, у Pascal існує ще один тип виразів – логічний.

Логічним виразом називається такий вираз, внаслідок обчислення якого одержується логічне значення типу true або false («істина» або «хиба»).

Із  стандартним типом змінних Boolean, які можуть набувати лише двох значень True або False, ви вже ознайомилися. Отже, саме такий тип і мають результати обчислення логічних виразів.

Логічні вирази поділяються на прості та складені.

Простим логічним виразом називається вираз, який записується за допомогою знаків співвідношень <, >, <=, >=, =, та <>.

Приклади простих логічних виразів можуть здатися вам простими:

а + b > с + d, n > т, х = у.

Порівняйте тепер призначення символів «:=» та «=»! Зверніть увагу на те, що спочатку виконуються арифметичні дії, а вже потім порівняння отриманих результатів.

Складеним логічним виразом називається вираз, в яко­му використовуються логічні операції and, or, not («так», «або», «ні»).

Наведемо приклади. З математики вам відомі такі записи:
х Î [а, b] та х Ï [a, b].

Спробуємо записати їх у вигляді логічних виразів

(х >= a) and (х <= b),

(x<a) or (x>b).

Під час запису складених логічних виразів прості логічні вирази обов'язково слід брати у круглі дужки!

Чи можна записати простий логічний вираз n<>m у вигляді складеного? Виявляється, можна:

not (n = m).

Визначимо правила, за якими обчислюються значення складених логічних виразів. Для цього існують таблиці істинності, в яких цифра 0 означає false, а цифра 1 - true. Наведені таблиці можна перефразувати таким чином.

Логічна операція and дає результат true тоді і тільки тоді, коли обидва операнди мають значення true.

Логічна операція or дає результат true тоді, коли хоча б один операнд має значення true.

Логічна операція not завжди дає результат, протилежний значенню її операнда.

Приклад. Нехай x=3, y= -9. Розглянемо деякі логічні вирази та їхні значення.

Подвійну нерівність 1<х<5 як складений логічний вираз запи­сують так: (1<х) and (x<5). Сукупність нерівностей вигляду х<1; х>5 — так: (х<1) or (x>5). Прості логічні вирази, які входять у складені,  завжди беруть у дужки.

2. Логічні змінні

Логічні змінні. Значення логічних виразів можна надавати
логічним змінним. Це скорочує текст програми.

Для роботи з логічними змінними є тип даних boolean. Нагадаємо, що логічних сталих є лише дві: true  і false.

Логічні змінні треба описувати у розділі оголошення змінних так:

var <список імен змінних>: boolean;

Наприклад, var z, z1, z2: boolean.

Нехай х = 2. Якого значення набуде змінна z2 після виконання таких трьох команд присвоювання:

z := х > 5;   z1:= not z;   z2 := z or z1 ?

Відповідь: тут z=false, a zl=true, тому змінна z2 матиме значення «істина» (true).

Довідка. Логічним змінним не можна надавати значення в діалоговому режимі командою read, однак їх можна виводити на екран командою write.

Задача. Нехай а, b, с — коефіцієнти квадратного рівняння ax²+bх+с=0. Відповісти на запитання: вислів «Квадратне рівняння має два дійсні різні корені» є істинний чи хибний?

Розглянемо програму Lohika.

program Lohika;

var a, b, с : real; L : boolean;

begin

write ('Введіть числа a,b,c: '); readln (a, b, c); L :== b*b-4*a*c> 0;

writeln ('Квадратне рівняння має два дійсні різні корені — ', L)

end.

Якщо під час виконання програми ввести три числа, наприклад, 2.5 8.1 -2.9, то на екрані отримаємо:

Квадратне рівняння має два дійсні різні корені — TRUE.

Висновок

Таблиця пріоритетів арифметичних і логічних операцій має такий вигляд:

1              ( )   — спочатку виконуються дії в дужках

2              Функції, логічна операція not

3              *, /, div, mod, and

4              +, -, or

5              >, <, >=, <=, =, <>

Умовою безпомилкового виконання таких операторів є збігання типів, тобто змінні в лівій частині цих операторів повинні бути описані типом boolean.

По-друге, результат обчислення логічних виразів true та false можна ще трактувати як «так» та «ні». Це наводить на думку про використання логічних виразів для визначення оцінки деякої ситуації, що склалася, і прийняття рішення про те, що робити далі.

V. Фізкультхвилинка для очей

VI. Закріплення теоретичного матеріалу

Дайте відповіді на запитання

І. Для чого використовують логічні вирази?

2. Що таке простий логічний вираз?

3. Які є символи відношень між величинами?

4. Що таке складений логічний вираз?

5. Які є логічні операції?

6. Дайте означення логічної операції not.

7. Дайте означення логічної операції and.

8. Дайте означення логічної операції or.

9. Який пріоритет логічних операцій?

VIІ. Формування практичних навичок

Розв’язати вправи та задачі

1.Усно. Чи істинний простий логічний вираз х > 10, якщо:

а) х=0;   б) х=2;   в) х=10;   г) х=5;   д) х=15?

2.Усно. Чи буде хибним вираз х >= 10, якщо:

а) х=1;   б) х=3;   в) х=10;   г) х=12;  д) х=25?

3.Чи істинний складений логічний вираз (х > 1) and (x < 5), якщо:

а) х=0;   б) х=2;  в) х=10;   г) х=5;   д) х=15?

4.Чи істинний складений логічний вираз (х <= 8) and (x > 3),   якщо:

а) х=0;   б) х=2;   в) х=10;   г) х=5;   д) х=15?

5.Якого значення (true чи false) набуде вираз (х <= 2) or (x > 5),   якщо:

а) х=0; б) х=2; в) х=10; г) х=5; д) х=15?

6.Запишіть логічні вирази для нерівностей:

а) 0<х<10 (відповідь: (х>=0) and (x<10) );    б) -5<х≤8;    в) 2<х≤7; г) х≤1 або х>9;    д) х≤2,  х>12;   є) х≤0 і у³0.

VIIІ. Підбиття підсумків уроку

1.     Підсумки роботи учнів на уроці, оголошуються та виставляються в журнал оцінки.

2.     Чи навчилися того, що планували.

ІX. Домашнє завдання.

Вивчити теоретичний матеріал уроку за конспектом.

1. Запишіть логічний вираз для визначення, чи точка х належить відрізку:
а)  [0;   3)  (відповідь:   (х>=0)  and (х<3)  );  б)  [-5;   5);   в)  [10;  20];

г) [2;14] або [20;25];    д) [4;10] і [8; 12].

2.Запишіть нерівності, які відповідають логічним виразам:

а)(х>2) and (x<=20) (відповідь:   2<х<20 );

б)(х<-2) or (х>15);        в) (х>=5) and (x<25);

г) (х>3) and not (х>5);   д) (х>=-5) and (x<5) or (x>0).